基于表面粗糙度修正的冷却风扇数值模拟方法研究

傅佳宏，张 宇，肖宝兰，张旭方，左 强

(浙江大学城市学院 工程学院， 杭州 310015)

轴流式冷却风扇在工业领域具有广泛的应用，对其性能进行精准的数值模拟研究，在冷却系统匹配、节能减排、气动噪声抑制等方面具有重要的工程应用意义[1-2]。风扇旋转时，通过具有不同压力曲线的风扇叶片与空气、护风罩之间复杂的双向流固耦合[3-4]及周期性作用，形成旋转流场与风扇前后的静压升。

目前，工程领域的主流风扇性能预测模型是多重参考坐标系(MRF)计算模型，该模型将风扇流动区域定义在旋转坐标系下，其它区域定义在静止参考系下，通过坐标系的不断重建来模拟风扇的旋转。由于模型中包含详细的风扇叶片几何信息，可以直接模拟出压力阶跃以及旋转流场等风扇特性，在预测精度及计算资源的消耗方面具有相当的优势[5-6]。由于采用了定常的近似求解，如何对MRF方法进行修正，进一步提高其模拟精度仍然面临着挑战。Wang等[7]研究了风扇旋转区的选择对其性能的影响，认为风扇旋转区应该为护风罩所包含区域，而不仅仅是风扇直径与厚度形成的圆柱区。Shankar等[8]采用MRF模型建立了风扇的数字风洞实验室用以进行实际风扇的修正。Gullberg等[9-11]认为对于风扇旋转流体区域的选择要包括与风扇有剧烈相互作用的区域和风扇附近非对称旋转部件，并提出将风扇转速提高14%所得的数值模拟结果可很好地与实验值进行匹配。Sengupta等[12]指出，通过MRF模型旋转流体区域、紊流模型、风扇网格质量进行一定的适应性修正后，完全可以达到工程实际的需求。耿丽珍等[13]采用MRF进行了风扇噪声分析方法的数值仿真研究。肖红林等[14]研究指出可以采用减小风扇和导风罩之间的间隙的方法来提高风扇模拟的精度。倪计民等[15]采用MRF方法研究了风扇与导风罩之间相对位置关系对于冷却风扇性能的影响，得到不同风扇具有不同最佳安装参数的结论。石海民等[16]进行了多风扇之间的MRF建模方法研究。

在上述的MRF计算模型修正中，都将风扇表面作为水力光滑面处理，而实际风扇表面粗糙度对于风扇表面涡的流动阻力以及壁面函数都有一定的影响。文中结合壁面函数，通过第一层网格离壁面的无因次距离y+，在湍流计算中加入粗糙度函数对壁面律做出修正，使得风扇表面更贴近实际情况，进一步提高风扇的数值模拟精度。

1 风扇表面粗糙度修正

通常粗糙度由表征粗糙颗粒类型的粗糙度常数Cs与粗糙度高度Ks决定，共同组成了粗糙度影响因子ΔB，对于风扇叶片表面，影响公式为[17]

(1)

(2)

其中,ν为流体运动粘度。粗糙度影响因子ΔB的定义式为

(3)

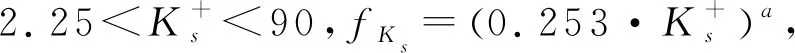
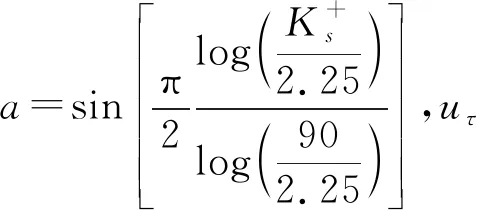
引入无量纲参数u+与y+，分别为第一层网格离壁面的无因次速度与距离：

(4)

(5)

其中：u是流体的时均速度；Δy是到壁面的距离；μ是流体的动力粘度。

对于黏性底层有u+=y+，从而得到风扇叶片表面摩擦速度uτ为

(6)

联立式(5)与式(6)可得到粗糙度高度Ks与风扇叶片第一层网格高度Δy的迭代方程组：

(7)

通过对风扇表面粗糙度的修正，可以让风扇的数值模拟更接近实际情况，结合网格、湍流模型等因素进一步分析修正后风扇数值模拟结果，并进行实验验证。

2 风扇数值模型的构建

2.1 MRF模型

通过风扇三维实体模型建立风扇数值仿真模型，采用MRF模型进行风扇性能仿真，其主要方法是在风扇流体区域建立多重参考坐标系，坐标系能够随着流体的旋转而不断重建。固定坐标系与移动坐标系中的速度矢量按照如下关系转换[18]：

Vr=v-(Vt+w×r),

(8)

式中，Vr为移动坐标系参考速度;V为绝对坐标系速度;Vt为坐标系移动速度;W为旋转角速度;r为风扇半径。

根据以上变换，在风扇旋转流体区域中，控制方程组为

(9)

2.2 边界条件的设置

以某半径为762 mm的车用冷却风扇为例，采用风扇周期性边界条件，分析紊流模型、叶片表面粗糙度、近壁面网格处理、网格无关性等对于风扇数值模拟结果的影响，从而提高风扇数值仿真精度。模拟风扇共有10片叶片，风扇直径为762 mm，转鼓直径为245 mm，给定风扇转速为2 100 r/min，如图1所示。

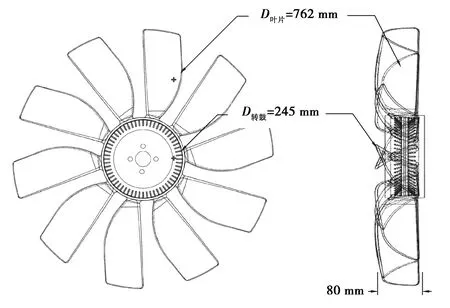
图1 风扇几何模型示意图

设置初始迭代条件为y+，得到Δy=0.000 892 m，Ks=0.000 046 4 m，因此，在设置边界层网格时，取边界层网格厚度为0.9 mm，叶片表面摩擦度高度为0.046 4 mm。

风扇采用周期性旋转边界建立风扇数值模拟风洞，风扇为十叶片均布，风扇的旋转偏移角为36°，设置风扇入口段半径与风扇半径一致，出口段为了使风扇的流动能够充分发展，取其半径与长度皆为入口段的2倍，如图2所示。

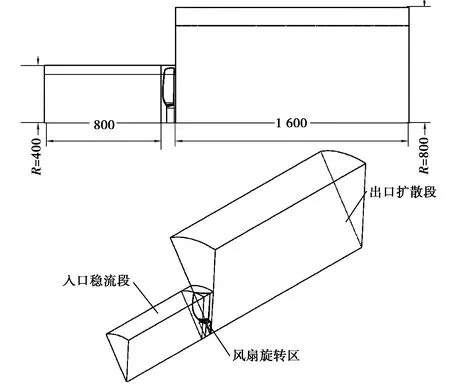
图2 风扇数值模型示意图

风扇流场采用MRF模型进行稳态数值计算，由于没有热交换器参与热交换，忽略能量方程，设置流动介质空气的物性参数为常物性；入口与出口分别设为压力入口与压力出口，表压设置为0 Pa；采用基于压力修正的SIMPLEC算法进行流场计算，采用二阶迎风格式进行网格的离散，当残差小于等于10-4次方时认为计算收敛。数值模拟在20核，32 G内存，2 T硬盘高性能工作站上进行，每个case根据网格数量的多少大约在1.5～3.0 CPU时收敛。

3 实验验证

按照如图3所示的工业通风机标准化风道上进行数值模型的试验验证。试验时通过改变调速电机的转速来控制风扇转速，通过改变节流加载板的孔隙率来改变风道的进气阻力，从而得到风扇在不同转速n下的风扇流量qv与静压H曲线。具体可参照文献[19]。

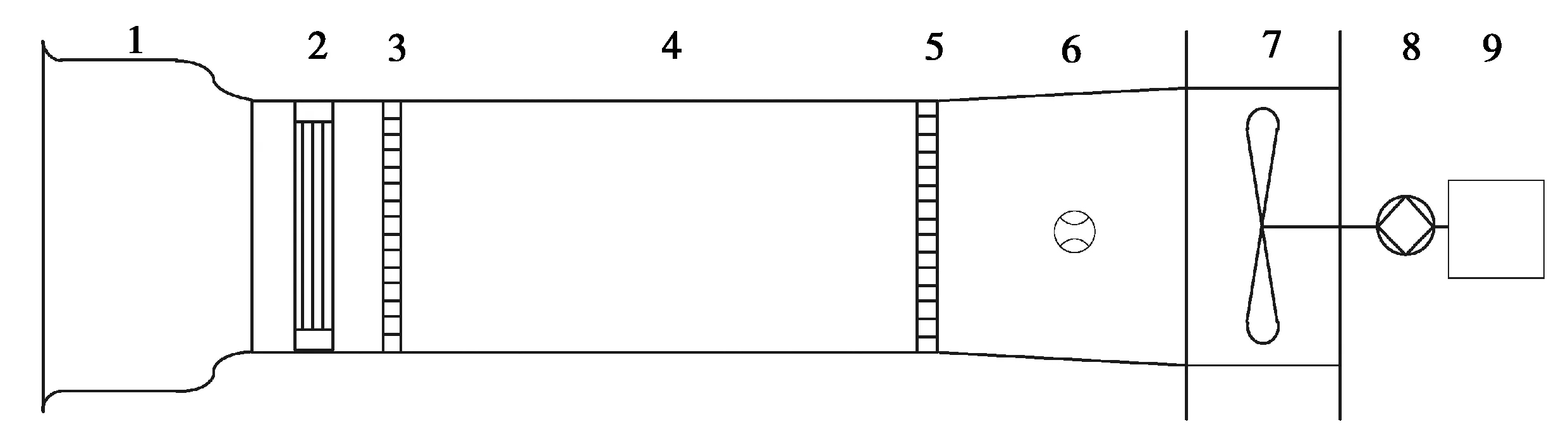
注：1.锥形集流器；2.节流加载板；3、5.整流器；4.试验风筒；6.空气流量计；7.风扇；8.扭矩转速传感器；9.调速电机

风扇全压ptp为冷却空气通过风扇后总压的升高量，包括冷却空气静压与动压之和，可表示为

(10)

风扇静压H表示为

(11)

其中：pout，pin分别为风扇出口和进口处静压，通常pout与大气环境相连，可认为pout=0；cin、cout分别为风扇进出口轴向速度，由于风扇进出口截面积大致相等，可认为cin=cout；ρ为空气密度；n为风扇转速，r/min；qv为风扇流量，m3/s。

4 数值仿真结果分析

4.1 网格无关性分析

不同网格密度下得到的风扇网格无关性分析，如图4所示。图4(a)为当风扇转速为2 100 r/min，流量为0.5 m3/s时，风扇的静压值随着网格密度变化的规律。图4(b)为风扇转速为2 100 r/min时，不同网格密度下得到的风扇性能曲线。

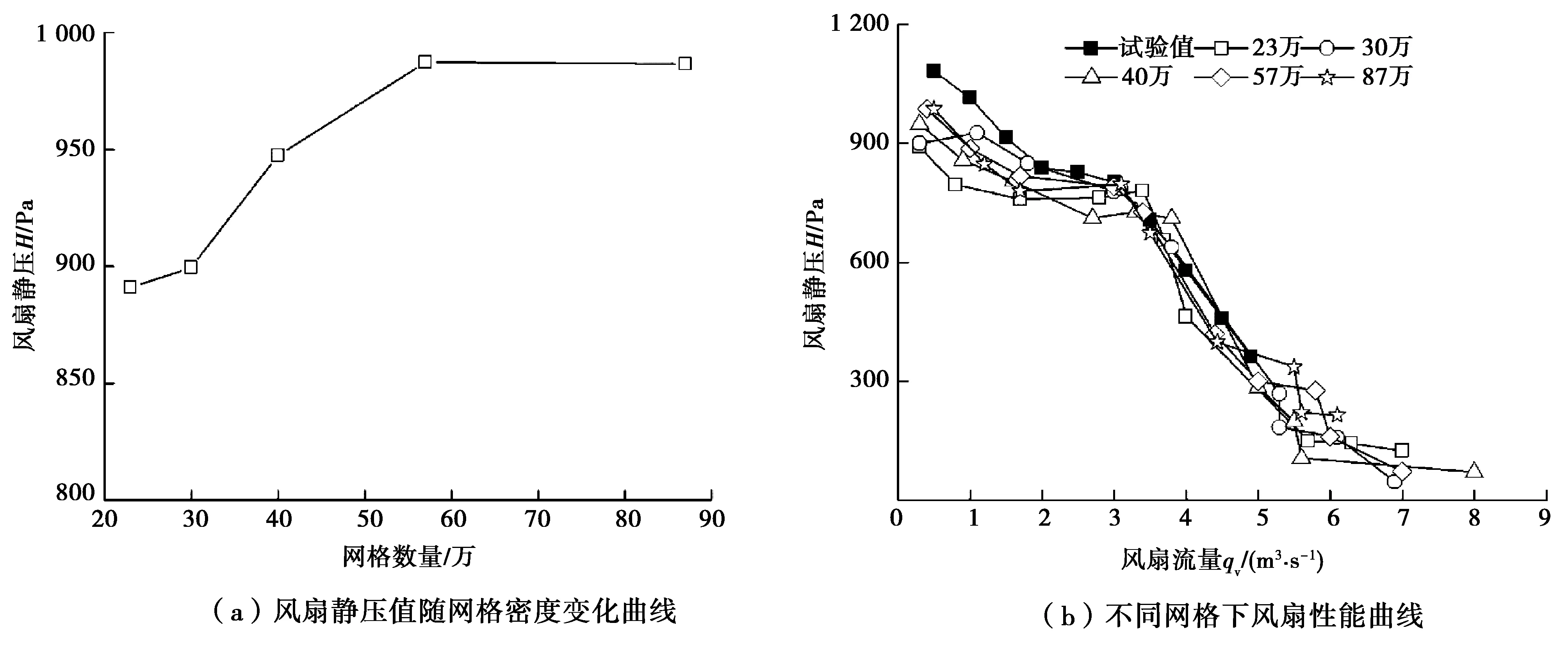
图4 风扇数值模型网格无关性分析

可以看出，随着风格的增加，静压值不断增加，当风扇旋转流体区域网格增加到57万时，随着网格的增加，风扇静压值几乎不变。在各个网格密度下，风扇性能曲线趋势基本一致，主要在曲线的两端距试验值有一定的偏差，当网格数量小于30万时，数值仿真结果偏差较大，随着网格数量的增加，偏差逐渐减小；然而当网格密度达到87万时，数值仿真结果并没有显著的改善，反而在流量超过5 m3/s时，静压值上出现了明显的流量波动。因此，最后选取风扇旋转流体区域网格为57万。

4.2 湍流模型对比分析

在计算风扇旋转流场等有强旋流和有弯曲壁面的流动时，可能出现时均应变率特别大的情形，采用标准k-ε模型时，针对此情形有可能产生负的正应力，从而导致流动失真，因此，在对具有旋转流动的流场进行数值模拟时，通常采用考虑旋转流场的RNG k-ε模型或者能够反映主流时均应变率的Realizable k-ε模型。

相同风扇旋转流体区域下，分别采用RNG k-ε模型和Realizable k-ε模型进行风扇数值模拟，不同的紊流模型对于风扇数值模拟精度的影响如图5所示。为了减小网格因素对于仿真精度的影响，采用加密网格进行数值计算，加密后，风扇网格数量为59万，计算工况为风扇转速2 100 r/min。

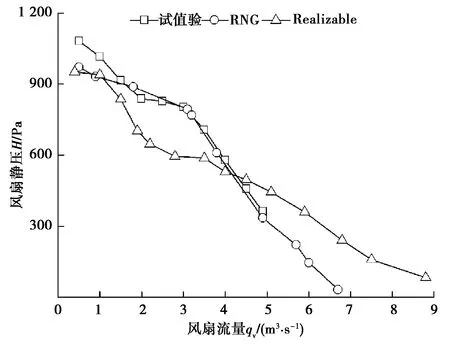
图5 不同紊流模型下风扇数值模拟结果对比

从图5中可以看出，相比Realizable k-ε模型，RNG k-ε模型具有更高的仿真精度，在风扇工作范围内(2～5 m3/s)，仿真值与试验值吻合较好，误差小于5%，但在低流量区域(0～2 m3/s)误差较大。因为在低流量、高静压工况下，湍流模型自身的局限性及风扇叶片压力面和吸力面之间的高压力梯度，RNG k-ε紊流模型在极端情况下不能很好地模拟出风扇的流动特性，但在风扇常用工况点，该模型具有足够的精度，具有一定的工程实用价值。

Realizable k-ε模型在整体趋势上能够模拟出风扇的气动特性，但是存在较为明显的过度模拟现象，主要表现为在中低流量工况(0～4 m3/s)下，仿真静压值要明显小于试验值，但是在大流量工况(>4 m3/s)下，仿真静压值又要明显大于试验值，因为数值仿真将光滑风扇叶片进行了人为的离散，无法完全模拟出光滑表面，在局部可能出现高曲率的情况，导致应变率出现极值点，影响了整个风扇的数值仿真精度。

4.3 粗糙度修正结果分析

采用近壁面粗糙度修正与仅采用简单壁面函数的风扇数值仿真结果与试验值的对比如图6所示。可以明显看出，在增加了近壁面处理后，数值仿真结果更接近试验值，因为其流动更符合实际情况，虽然在低流量区域静压值与试验值还是存在100 Pa左右的偏差，但经过近壁面处理后风扇性能曲线更为平顺，改善了未经过近壁面处理时产生的一些畸点，且在风扇常用工况范围内(2～5 m3/s)，试验值与仿真值的偏差在3%以内，完全可以满足工程应用的需要。

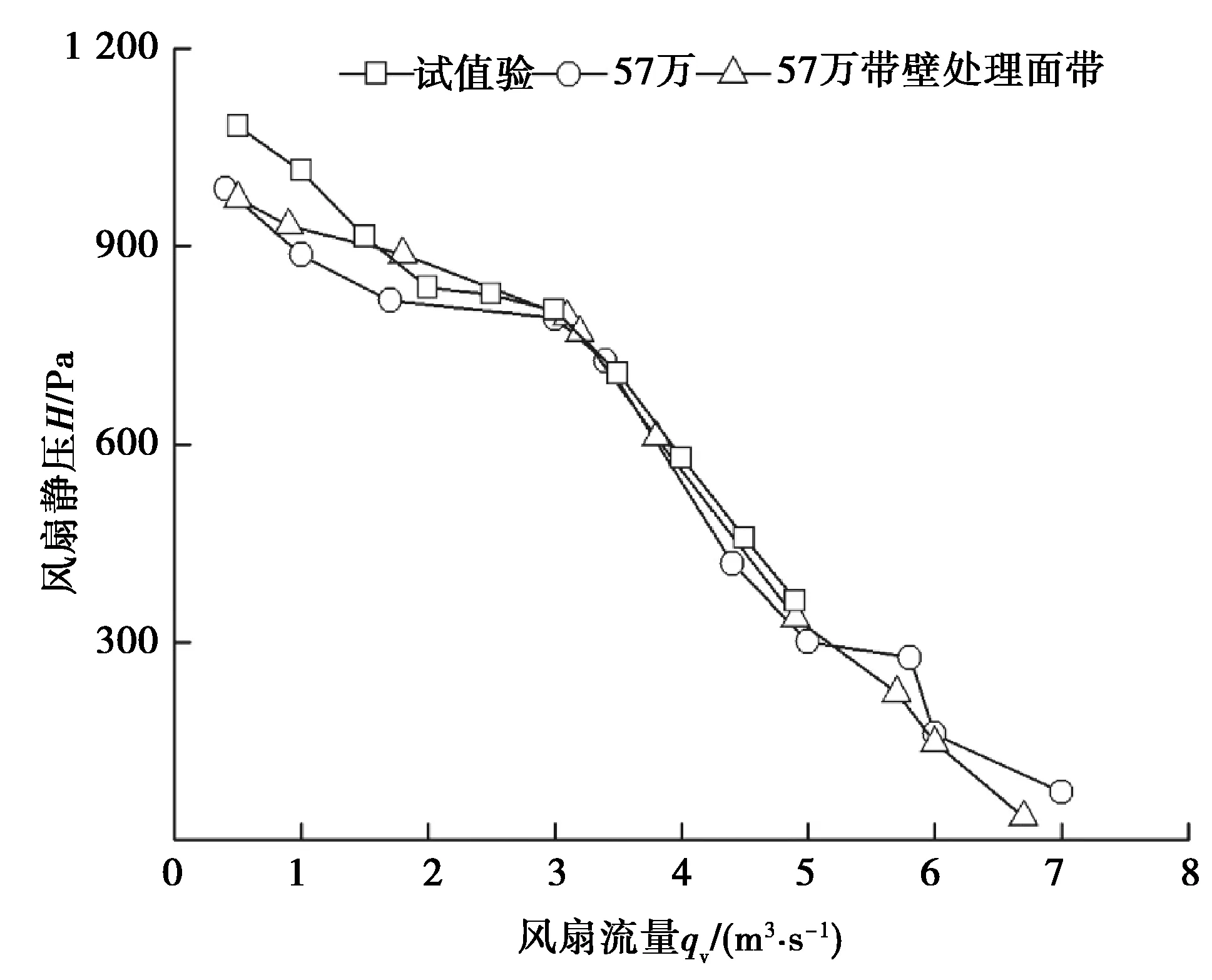
图6 壁面处理前后计算结果对比

图7所示为比较得到的相对较好的57万网格数量，RNG k-ε紊流模型，表面粗糙度修正之后，风扇在各个转速下的数值模拟结果与试验值的对比，从中可以看出，除了高压低速区，试验值与模拟值都能较好的吻合，可见文中提出的风扇数值模拟方法可以提高全工况范围内风扇性能的数值模拟精度。

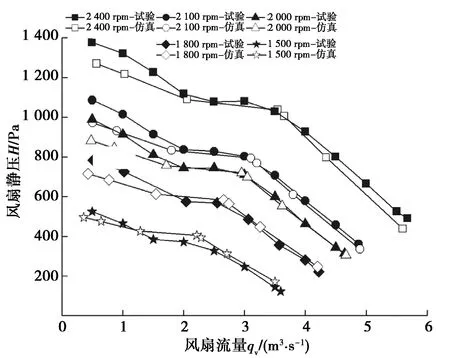
图7 风扇性能试验值与理论计算值对比

5 结 论

1)分析比较了Realizable k-ε紊流模型与RNG k-ε紊流模型对于风扇数值仿真精度的影响， 发现后者在常用工况点具有足够的精度与计算效率。

2)常用风扇MRF计算模型基础上增加了风扇叶片表面摩擦度修正，提高了风扇数值仿真精度。

3)通过全转速下的风扇模拟与试验验证，证明了该方法的普适性，可以采用风扇相似定理得到不同转速下的风扇性能。