集料模量对钢桥面铺装层间剪切疲劳影响的细观数值模拟
魏 鹏,王思琦,刘 云
(1.江苏纬信工程咨询有限公司,南京 210014;2.华设设计集团股份有限公司,南京 210014;3.河海大学道路与铁道工程研究所,南京 210098)
钢桥面沥青铺装层直接铺设在正交异性钢桥面板上,产生的主要病害是由于沥青铺装层与钢板之间黏结不紧密而造成的层间剪切疲劳破坏[1-3].目前,我国对钢桥面铺装的研究主要集中在探究钢桥面层间抗剪性能方面,如姚波等[4-5]通过自制的钢桥面铺装复合结构层间剪切试验装置,研究不同温度和法向应力对层间抗剪强度的影响,随着温度的降低和法向水平应力的增加,复合试件层间抗剪强度逐渐增大;于昌权等[6]通过室内试验研究不同养生方式下温湿耦合作用对钢桥面铺装层间剪应力的影响,发现空气湿度是钢桥设计不可忽视的影响因素;徐恭圣等[7]基于室内试件建立钢桥面铺装复合结构离散元模型,模拟两种温度情况下复合结构的层间剪切破坏行为,分析层间失效行为和裂缝的产生情况;柳富勇等[8]利用有限元软件建立复合结构有限元模型,模拟结构在不同轴载和不同模量铺装下的应力分布,从而推算铺装层疲劳发展情况.目前,针对钢桥面铺装层间剪切疲劳破坏的研究较少,室内试验与数值模拟只从宏观角度研究钢桥面铺装复合结构的层间力学响应,不能从细观角度分析层间疲劳破坏机理,因此,本文采用离散元数值模拟方法[9-11],从细观层面分析粗集料模量对钢桥面铺装复合结构层间剪切疲劳破坏的影响规律,为钢桥面铺装结构的设计提供参考.
1 钢桥面铺装复合结构三维细观模型的构建
1.1 模型的构建
在PFC3D中,构建的沥青铺装层尺寸为100 mm×100 mm×60 mm,沥青混合料为AC-10,油石比为4.9%[7].在建模时,先把沥青铺装层分为粗集料和沥青砂浆两相,根据沥青混合料级配,将小于2.36 mm的颗粒单元作为沥青砂浆,将大于或等于2.36 mm的颗粒单元作为粗集料,基于相互重叠算法,形成由半径为1 mm球单元组成的粗集料单元和沥青砂浆单元,在随机删除一定数量的沥青砂浆单元形成空隙,最终得到具有级配特征并且考虑空隙的沥青铺装层三维离散元模型[12-14].
离散元模型中并未单独建立黏结层,是因为黏结层的厚度相对于沥青铺装层和钢桥面板来说非常小,并且在PFC3D软件中,平行黏结模型可以用来描述颗粒间有限尺寸内有夹层材料或胶结材料的本构特性,于是采用平行黏结模型来表示沥青铺装层颗粒与钢桥面板颗粒之间的接触本构模型,从而达到模拟黏结层的效果.
离散元模型中钢桥面板尺寸为100 mm×100 mm×10 mm,该部分建模通过在指定区域内生成规则排列的、半径均为1 mm的小球单元,即可完成钢桥面板的构建.
将沥青铺装层模型与钢桥面板模型组合起来,即可得到钢桥面铺装复合结构试件模型,如图1所示.
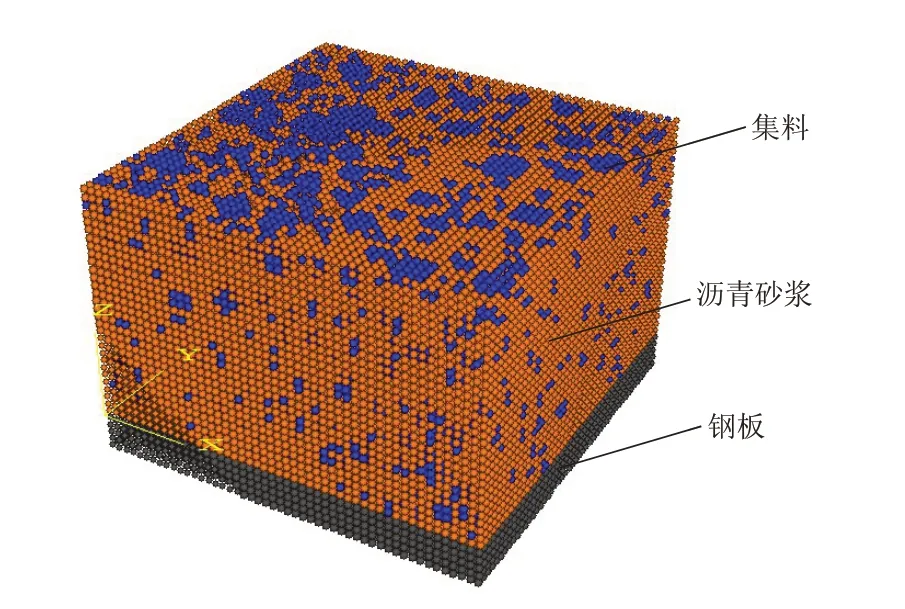
图1 钢桥面铺装复合试件三维离散元模型Fig.1 Three-dimensional discrete element model of composite specimens for steel deck pavement
1.2 单元接触模式与参数
在PFC3D中,接触本构模型主要包含三个部分:刚度模型、滑动模型和黏结模型[15].针对所建的钢桥面铺装复合结构模型不同单元之间的接触特点,本文所选的接触本构模型如表1所示.

表1 接触本构模型的选取Tab.1 Selection of contact constitutive model
在PFC3D中,材料性能是通过细观参数表现的,而根据研究,细观参数可以通过宏观力学推导获得[16].上述的接触本构模型中,除Burgers模型外,其余线弹性模型的细观参数通过式(1)确定:

式中:Kn为法向接触刚度;R为半径;E为材料杨氏模量.
对于Burgers模型,根据室内30℃沥青动态蠕变试验以及Liu等[17-18]建立的换算公式,得到Burgers模型的细观参数如表2所示.

表2 30℃下Burgers模型细观参数Tab.2 Microscopic parameters of Burgers model at 30℃
2 虚拟疲劳试验
2.1 疲劳加载
疲劳应力的加载选用应力控制模式,荷载的频率取10 Hz,为连续半正弦矢波,峰值为1.7 MPa[14-15].力的加载是通过赋予加载墙体一定的速度来实现,通过加载墙体沿x轴负方向运动,实现对铺装层的疲劳剪切模拟.为了保证试验要求的控制应力,通过PFC3D中的“FISH”语言编写伺服控制程序,不断调整加载墙体的移动速度以达到试验控制应力的要求,监测的部分加载力波形如图2所示.
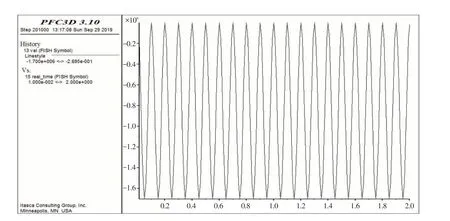
图2 监测的部分加载力波形图Fig.2 Waveform of partial loading force monitored
从图2可以发现,随着加载周期的增大,加载的剪切应力基本保持半正弦波波形,同时剪切应力的峰值稳定在1.7 MPa左右,这表明虚拟试验中疲劳加载满足原先设定的试验条件,从加载形式上来看,虚拟试验加载方式与室内试验基本相符.
2.2 加载20周期层间疲劳行为分析
根据室内试验研究,从复合结构层间剪切疲劳曲线可以发现,层间剪切疲劳破坏一般分为三个过程,即初始阶段、稳定阶段和破坏阶段.在疲劳加载的初始阶段(10周期左右),复合结构层间剪切位移变形速率较快,位移增长幅度较大,稳定阶段层间位移变形速率平缓,是试件疲劳寿命的增长阶段[19].考虑到加载应力1.7 MPa较大,试件出现疲劳剪切位移速率较快[20],于是本文选取疲劳剪切加载前20周期的层间疲劳行为作为研究对象,从结构层间位移、层间应力及层间颗粒黏结失效变化等方面,探究粗集料模量对钢桥面铺装层间剪切疲劳行为的影响,分别进行粗集料模量为49、55.5、62、68.5、75 GPa等不同工况下层间剪切疲劳虚拟试验.不同集料模量细观参数根据式(1)可以计算得到.
1)层间位移分析
不同集料模量加载20周期的荷载作用后钢板与铺装层层间的位移变化情况如图3所示,加载20周期层间最大位移如图4所示.
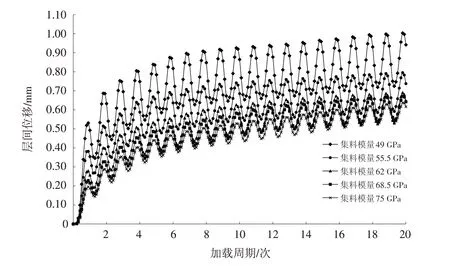
图3 钢桥面铺装复合结构层间位移-周期图Fig.3 Inter-story displacement-periodic diagram of composite steel deck pavement structure
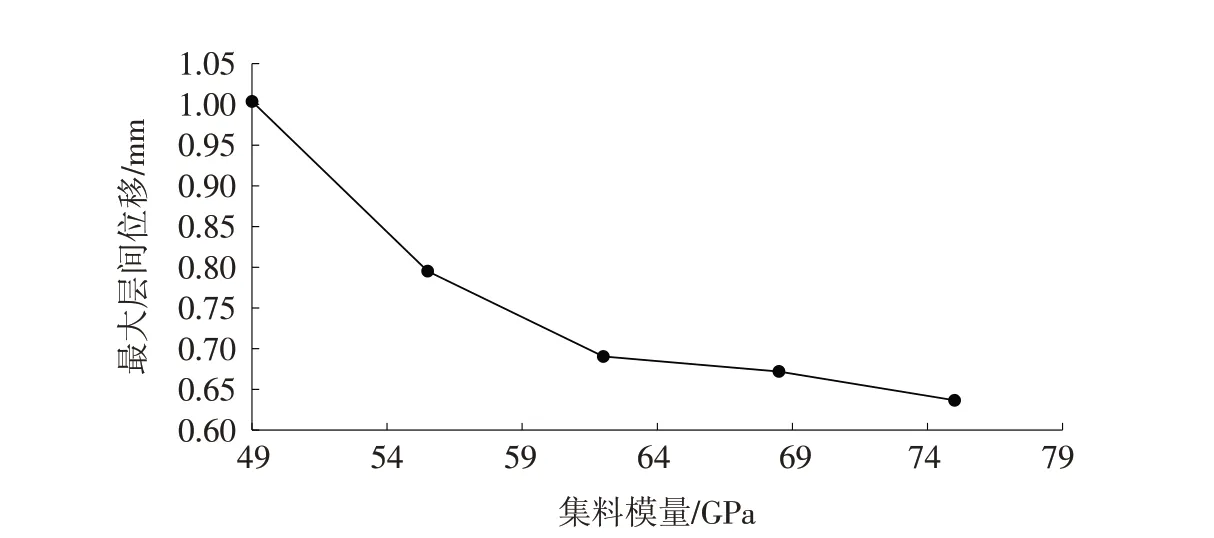
图4 不同集料模量层间最大位移图Fig.4 Maximum displacement diagram between layers with different aggregate modulus
从图3、图4可以发现:①钢桥面铺装复合结构在虚拟疲劳荷载作用下层间界面发生位移,且位移呈近正弦波曲线增长,这与加载的剪切疲劳荷载相吻合,进一步验证了模型的可靠性;②随着重复荷载作用次数的增加,当模量从49 GPa变化到75 GPa的过程中,加载20周期发生的最大层间位移依次为1.00、0.80、0.70、0.67、0.64 mm,层间剪切位移逐渐降低,说明集料模量越高,层间抗疲劳性能越好,适当选用高模量的粗集料可以提高钢桥面铺装层间结构的抗疲劳性能;③五种模量下层间位移降幅依次为20.8%、13.2%、2.6%、5.3%,说明黏结层结构抵抗外界疲劳荷载的能力在增强,尤其在55.5 GPa时性能表现明显,超过55.5 GPa后位移变化减弱,抗疲劳性能变化不突出,说明粗集料模量选用62~68.5 GPa范围内抗疲劳效果更突出.
定义各周期层间最小剪切位移为层间永久剪切变形,绘制五种模量下加载20周期层间剪切疲劳曲线[20]如图5所示.
从图5疲劳曲线可以发现:①在相同时间的疲劳作用下,粗集料模量越低,试件层间界面产生的永久变形越大,可以预测,随着加载的进行模量为49 GPa的试件最先破坏,其疲劳寿命最短;②从图中可以发现模量在49~75 GPa过程中,随着加载次数的增加,层间永久剪切位移的差距在缩小,说明集料模量的优势在减弱,基于经济性原则和抗疲劳性能,在进行铺装设计时选取的粗集料模量并不是一定采用高模量,推荐在62~68.5 GPa中选用;③在前10个周期,层间剪切位移急速增加,层间提供的摩阻力不足以抵抗外荷载作用,此阶段可定义为位移急速增长阶段,经历10周期的加载后,复合结构位移曲线增长趋于平缓,层间剪切变形率大幅降低,原因是在10周期的外力作用下,层间颗粒由于受力重新组合排列,提供层间抵抗外力的稳定的摩阻力,使得层间剪切变形率保持稳定,结构适应疲劳荷载,由此可以定义该阶段为层间位移进入平缓增长阶段.
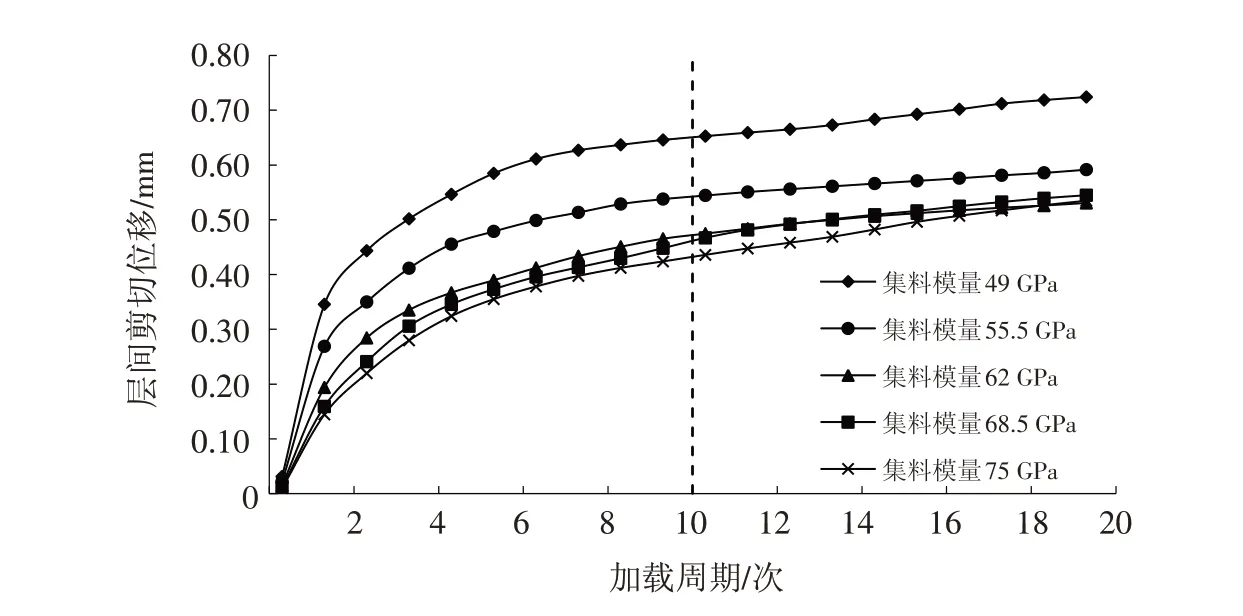
图5 不同集料模量下层间剪切疲劳曲线图Fig.5 Interlaminar shear fatigue curves with different aggregate modulus
2)层间剪切应力分析
五种集料模量下各周期层间最大应力变化如图6所示.
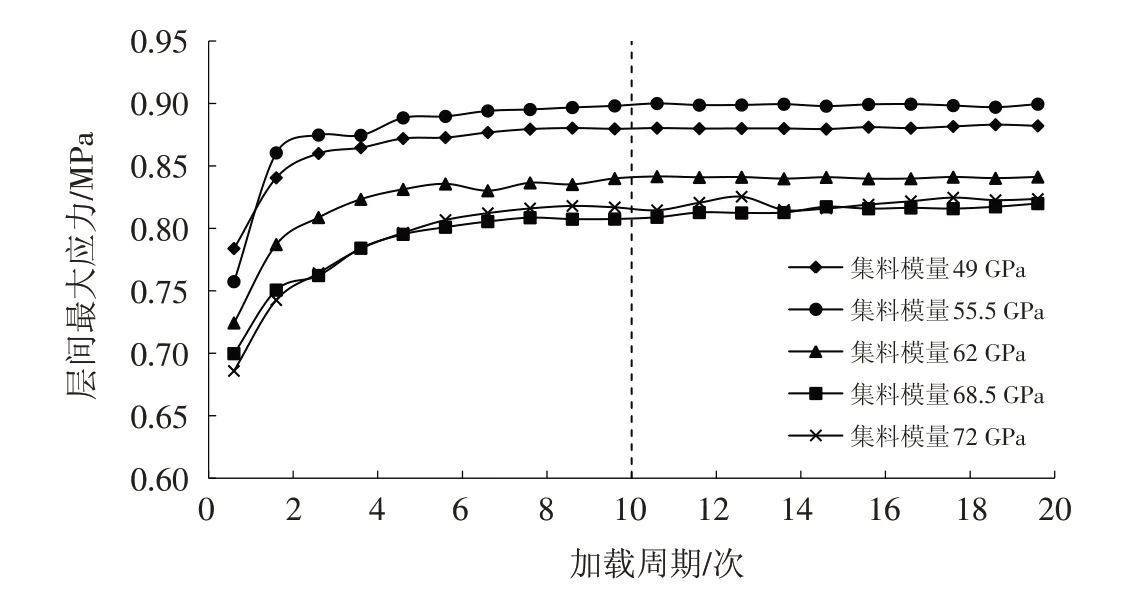
图6 不同集料模量下层间最大应力变化图Fig.6 Max-stress diagram of interlayer under different modulus of aggregate
从图6可以看出:①从层间应力极值来看,五种集料模量下层间应力大致趋于稳定,最大值均在0.85 MPa左右,差距较小,说明控制应力条件下,集料模量对层间剪应力的变化影响较小;②在0~5周期内,五种工况下层间应力增长幅度都在15%左右,5~10周期内,层间最大应力的增幅只有1%,随着达到10~20周期,应力增幅在0.2%左右,从20个周期的应力增幅来看,应力数值趋于稳定,由此可见,加载10周期后层间变形进入稳定发展阶段.
3)层间颗粒黏结失效发展分析
五种集料模量下加载20周期层间颗粒黏结失效数量变化如图7所示,这里主要通过FISH编程提取沥青砂浆单元与钢桥面板单元、粗集料单元与钢桥面板单元之间的黏结失效数量.加载20周期层间颗粒黏结失效位置分布图如图8所示.
从图7和图8可以发现:①在20周期的疲劳作用过程中,伴随着集料的模量增大,沥青铺装和钢板层间界面的黏结失效数量在减少,集料模量为49 GPa的复合试件较其余模量试件层间失效数量增长迅速,增幅在6倍左右,而模量在75 GPa的试件还未出现黏结破坏,说明模量较高的集料可以提高钢桥面铺装复合试件的层间抗疲劳剪切性能,延长路面使用寿命;②加载初期,层间黏结失效主要集中分布在加载侧附近,模量49 GPa的试件黏结失效颗粒分布较广,且向试件层间内部扩展,增速较快,其余试件失效颗粒较少,分布较为集中.
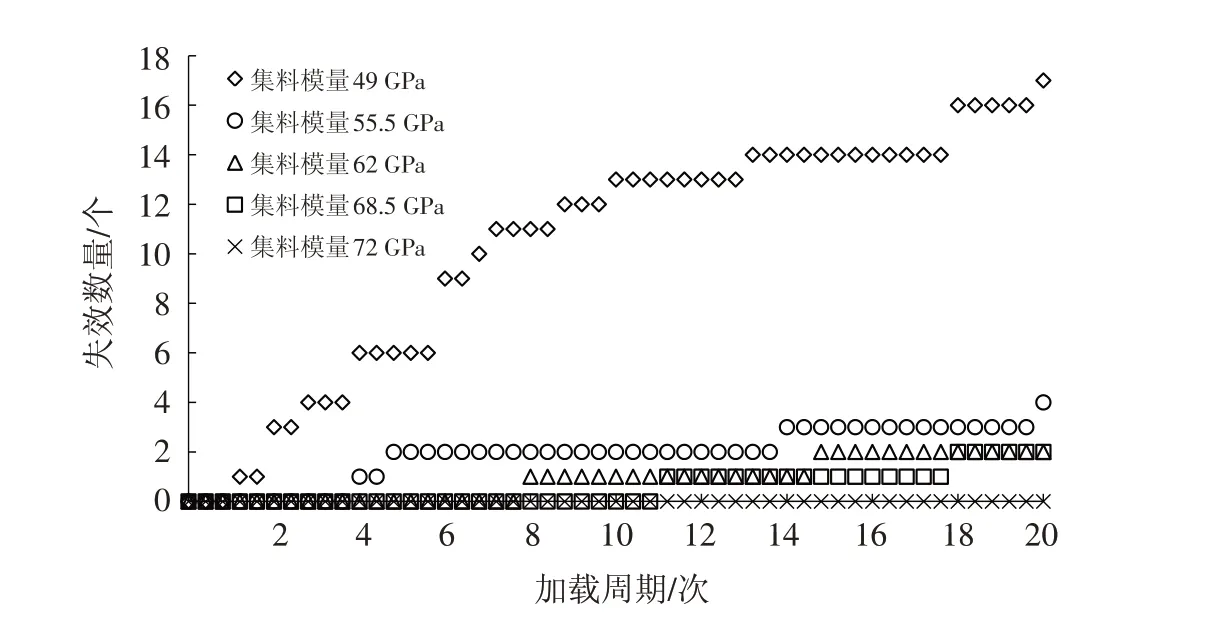
图7 不同集料模量下层间颗粒黏结失效数量图Fig.7 Number diagram of interlaminar particle bond failure under different aggregate modulus
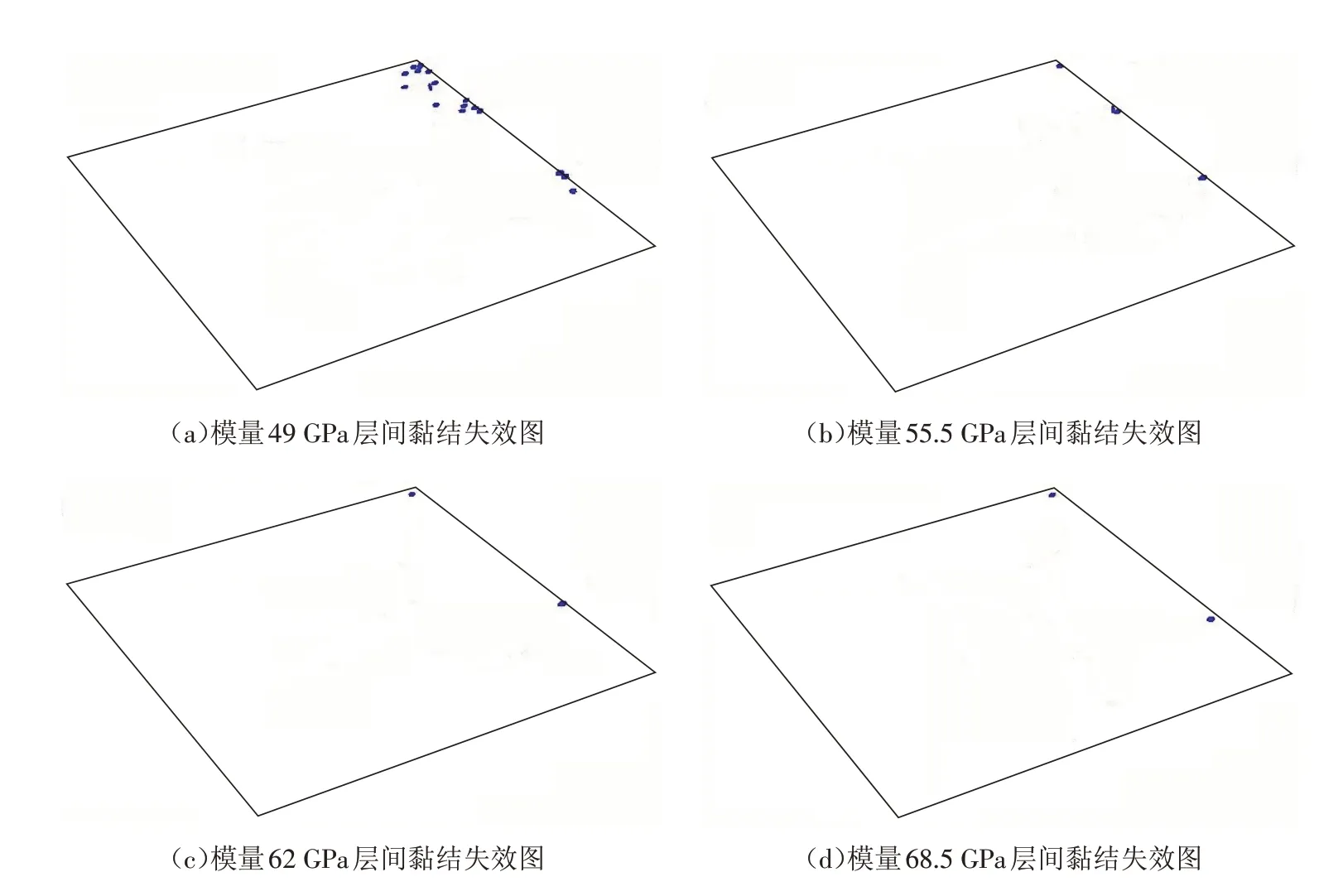
图8 不同集料模量下层间颗粒黏结失效分布图Fig.8 Failure distribution map of interlayer particle bonding under different aggregate modulus
从表3可以看出:①从时间上看,随着集料模量的增大,层间结合处第一个黏结失效颗粒出现的时间在增加,从49 GPa到68.5 GPa的过程中,时间从0.9个周期增加到11个周期,接近11倍,说明高模量的粗集料有效降低层间黏结失效的速率,提高了复合结构的层间疲劳寿命;②结合图8,从首个层间黏结颗粒脱黏时发生的层间位移来看,49、55.5、62、68.5 GPa模量的试件对应的层间剪切位移均在0.5~0.6 mm左右,可以预测的是,在疲劳荷载作用下试件出现疲劳脱层破坏时的剪切位移接近,说明集料模量不会改变试件破坏时铺装与钢板的相对位置.

表3 第一个颗粒黏结失效出现的时间与位移Tab.3 Time and displacement of the first crack
3 层间剪切疲劳评价指标分析
3.1 钢桥面铺装层间抗剪强度与层间疲劳性能的关系
为分析层间抗剪强度对钢桥面铺装复合结构层间疲劳性能的影响,将五种集料模量对应的钢桥面复合试件分别进行层间剪切模拟试验,加载方式与疲劳加载相似,通过控制加载墙体速度对铺装层施加剪切力,墙体速度固定为50 mm/min,加载直至试件脱层破坏停止.将五种集料模量对应的层间抗剪强度与进行20周期疲劳剪切作用产生的层间位移、裂缝进行比较,如表4所示.

表4 抗剪强度与疲劳性能关系表Tab.4 Shear strength and fatigue property relation table
从表4可以发现,在相同的加载周期作用下,层间抗剪强度大的复合结构层间位移小,并且裂缝生成的数量与速度明显低于层间抗剪强度低的复合结构,因此层间抗剪强度大的结构破坏所需的加载次数会更多,疲劳寿命也更长.抗剪强度越高,层间抗疲劳性能越优异,为了提高钢桥面铺装复合结构的使用寿命,可以适当提高混合料中粗集料的模量.
3.2 层间变形稳定阶段的剪切位移变化率
由前面论述可知,加载在10周期以后层间变形进入稳定发展阶段,定义该阶段层间位移每增加0.01 mm需要的加载次数为层间剪切位移变化率.五种集料模量下剪切位移变化率如表5所示.

表5 层间剪切位移变化率表Tab.5 Interlayer shear displacement variation rate table
从表5可以发现,随着集料模量的增加,复合结构层间每增加0.01 mm的位移,所需的加载次数逐步上升,结果表明,集料模量提高了层间黏结性能,抵抗变形能力增强;模量在62~68.5 GPa时变化率最大,说明该范围集料用于桥面的沥青铺装材料较为合宜,疲劳性能表现优异.
4 结论
1)沥青铺装中粗集料模量越低,复合结构层间抗疲劳性能越差,疲劳寿命越短,当集料模量在62~68.5 GPa范围内时,抗疲劳性能各方面表现优异,建议在进行铺装设计时采用该范围模量.
2)集料模量的改变对疲劳剪切过程中结构层间应力基本没有影响,各集料模量下层间黏结颗粒出现黏结失效时对应的层间剪切位移相近,时间上有差别,集料模量不会改变试件破坏时沥青铺装层与钢桥面板的相对位置.
3)钢桥面铺装复合试件层间抗疲劳性能与层间抗剪强度有关,表现为层间抗剪强度越高,层间抗疲劳性能越好,发生的层间剪切位移越小.

