基于图像回归的SAR图像变化检测

赵 锐

（商洛学院数学与计算机应用学院，陕西商洛 726000）

变化检测是指通过检测不同时刻同一场景下图像像素或纹理等特征之间的变化，获取感兴趣的地物或地表在位置、形状及其他属性的变化信息.全天时、全天候成像的独特优势使得合成孔径雷达（Synthetic Aperture Radar，SAR）图像更适合用于变化检测研究.近年来，SAR图像的变化检测已被广泛应用于军事侦察、自然及生态环境的实时监测［1］、自然灾害的评估［2］、农作物的分布及长势监测［3］、森林资源监测［4］、城市研究［5-7］等领域.

目前，针对SAR图像变化检测问题，国内外学者提出了许多解决方案［8］.但是由于SAR图像不可避免地受到相干斑噪声的影响，因此在变化检测过程中如何抑制噪声的影响显得尤为重要［9］.

由于光照、大气条件、环境等因素的变化，导致前后两时相SAR图像中未变化区域的像素灰度值之间同样存在差异.因此本文提出一种基于图像回归（Image Regression，IR）的变化检测方法，假设前后两时相SAR图像在未变化区域的像素灰度值之间是呈线性关系的，提取未变化区域内的样本，利用样本建立线性模型，再通过最小均方误差来估计线性模型的参数，最后利用线性模型重构变化后的图像.继而可以通过对真实SAR图像与重构图像进行差异度量得到差异图，并对得到的差异图进行分析，从而得到最终的变化检测结果.实验表明，本文提出的方法在一定程度上可以减少大气条件、入射角度以及环境差异等因素对变化检测精度带来的影响.

1 基于图像回归的差异图构造

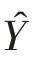
式中：a、b为线性函数的待定参数.为了估计参数a和b，定义真实SAR图像Y与重构图像Ŷ在样本点处平方误差如下：

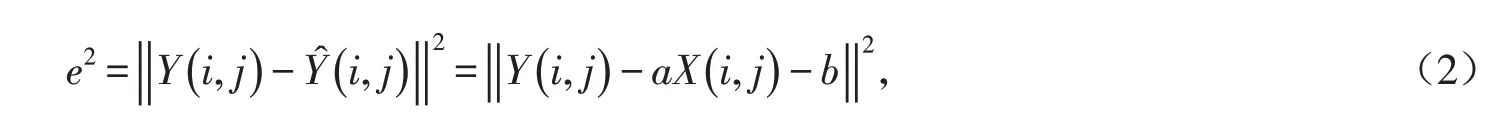
其中：‖‖·表示L-2范数.此时，平方误差总和为：

其中，假设有N1个具有低重构误差的像素点被选作样本点，通过最小化平方误差和S获得最优参数a、b.此时图像回归模型为：

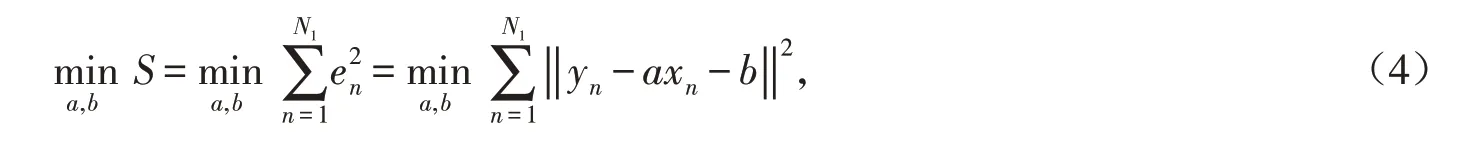
解得

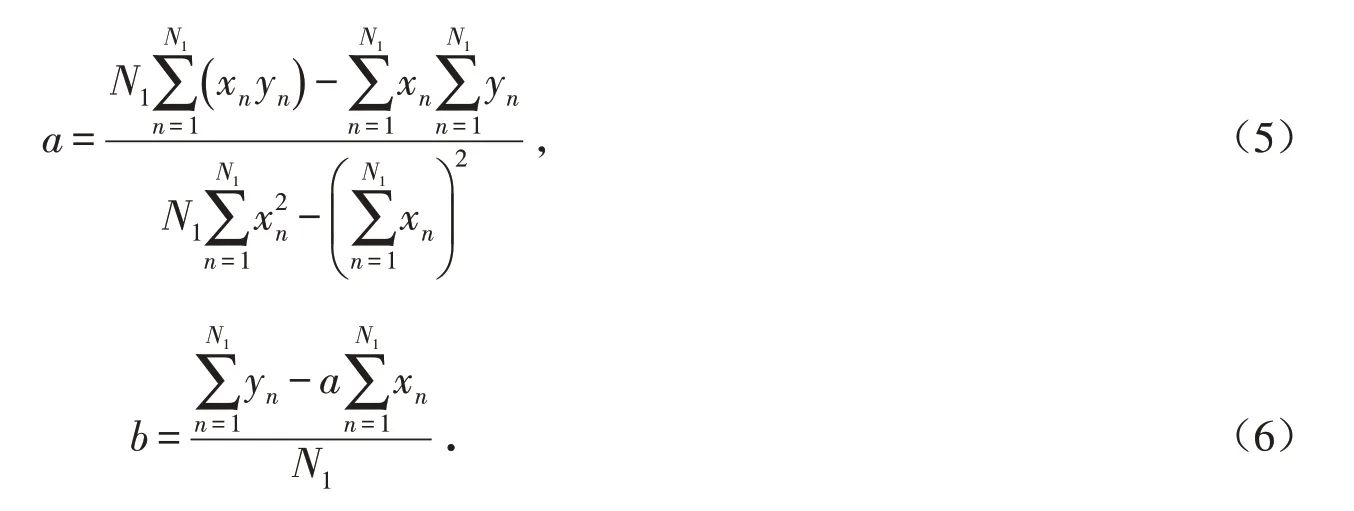
基于图像回归的差异图构造方法具体步骤如下：

步骤1：选取未变化区域具有低重构误差的像素点T={(X,Y)}={(xn,yn),1≤n≤N1}作为样本点；

步骤2：根据公式（5）、（6）求解拟合线性函数参数a和b；

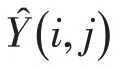
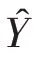
2 实验与分析

为了评估基于图像回归的SAR图像变化检测方法的有效性，针对四组两时相SAR图像数据集进行实验，选取的变化检测效果评价指标有：漏检数（FN）、错检数（FP）、总错检数（OE）、正确检测率（PCC）［11］和Kappa系数［12］.

2.1数据集描述

第一组SAR数据集［13］为模拟SAR数据集，其图像大小为256×256.该数据集的原始图像及变换检测结果参考图如图1所示.

图1 模拟SAR图像数据集图Fig.1 The simulated SAR data set images

第二组SAR图像数据集为Bern数据集.该数据集的原始图像是通过欧洲遥感2号星载SAR传感器（ERS-2）分别在1999年4月和1999年5月获得的瑞士Bern地区前后两时相图像［9］.该数据集的原始图像及变化检测结果参考图如图2所示.

图2 Bern数据集图Fig.2 Images for Bern data set

第三组SAR图像数据集为Ottawa数据集.该数据集的原始图像是通过Radarsat-1 SAR卫星分别于1997年5月和1997年8月获得的加拿大Ottawa地区的影像［14］，该数据集的原始图像及变化检测结果的参考图如图3所示.

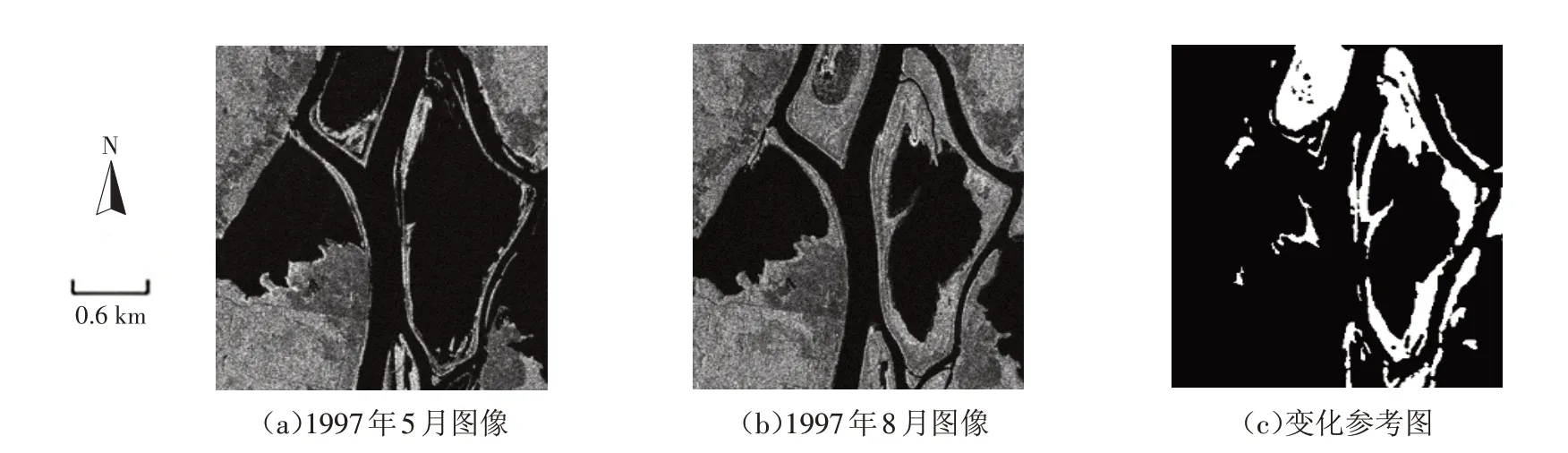
图3 Ottawa数据集图Fig.3 Images for Ottawa data set

第四组SAR图像数据集为Yellow River数据集.该数据集是由Radarsat-2 SAR卫星分别在2008年6月18日和2009年6月19日拍摄的黄河入海口区域的遥感影像［15］.该数据集图像大小均为257×289，其原始图像及变化检测结果参考图如图4所示.

图4 Yellow River数据集图Fig.4 Images for Yellow River data set

2.2 实验设置与结果分析

实验1以四组SAR图像数据集作为实验数据，研究图像回归算法中参数N1的选取对变化检测结果的影响；实验2中以比值算法、对数比值算法构造差异图为对比实验，分析了基于图像回归的差异图构造方法的性能.

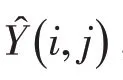
从图5分析可知，N1的变化对模拟SAR图像数据集、Bern数据集以及Yellow River数据集这三组数据集的最终变化检测结果影响较小，但对Ottawa数据集影响较大.这是因为本实验对模拟SAR图像数据集和Yellow River数据集进行了图像去噪这一预处理后图像变得平滑，从而利用样本点学习回归参数时，较少的样本点就可以使得图像回归模型参数a、b趋于收敛.从图5中可以看出，当N1≥1700时，PCC曲线增长变得平缓，从而在本文的实验中均设定N1=1700.针对本文的四组数据集，其样本点选取结果如图6所示.

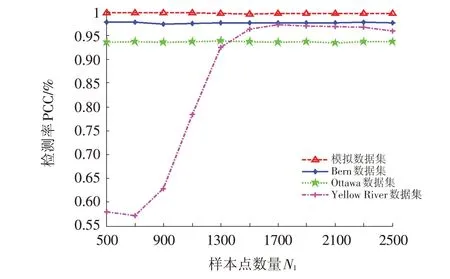
图5 四组数据集分别关于样本点数量N1与正确检测率PCC的曲线图Fig.5 Relationship curves between the parameter N1 and PCC on the four data sets

图6 样本点选取结果图（1700个样本点）Fig.6 Results of sample point selection（N1=1700）

2.2.2 实验2：基于图像回归的SAR图像变化检测方法的性能分析 在本实验中，针对以上四组两时相SAR图像数据集，评估基于图像回归的SAR图像变化检测方法的有效性，并将本文方法与经典的比值法以及对数比值法构造差异图进行比较.图7（a）～（c）、（d）～（f）、（g）～（i）和（j）～（l）分别对模拟SAR图像数据集、Bern数据集、Ottawa数据集以及Yellow River数据集采用三种不同的差异图构造方法得到的差异图像.图8给出了对四组SAR图像数据集利用三种不同的方法构造的差异图分别使用FCM聚类算法进行聚类得到的最终变化检测结果.从实验图中可以看出，针对四组SAR图像数据集利用比值法构造的差异图效果均欠佳，且图像回归算法相比其他两种差异图构造方法能够有效地抑制噪声的影响.表1是其对应的变换检测结果指标，从中可以看出，针对四组SAR图像数据集本章提出的基于图像回归的差异图构造方法与比值法、对数比值法相比性能均得到提高，其正确检测率分别为97.89%、99.31%、96.92%、93.37%，从而验证了利用图像回归算法构造差异图的有效性.

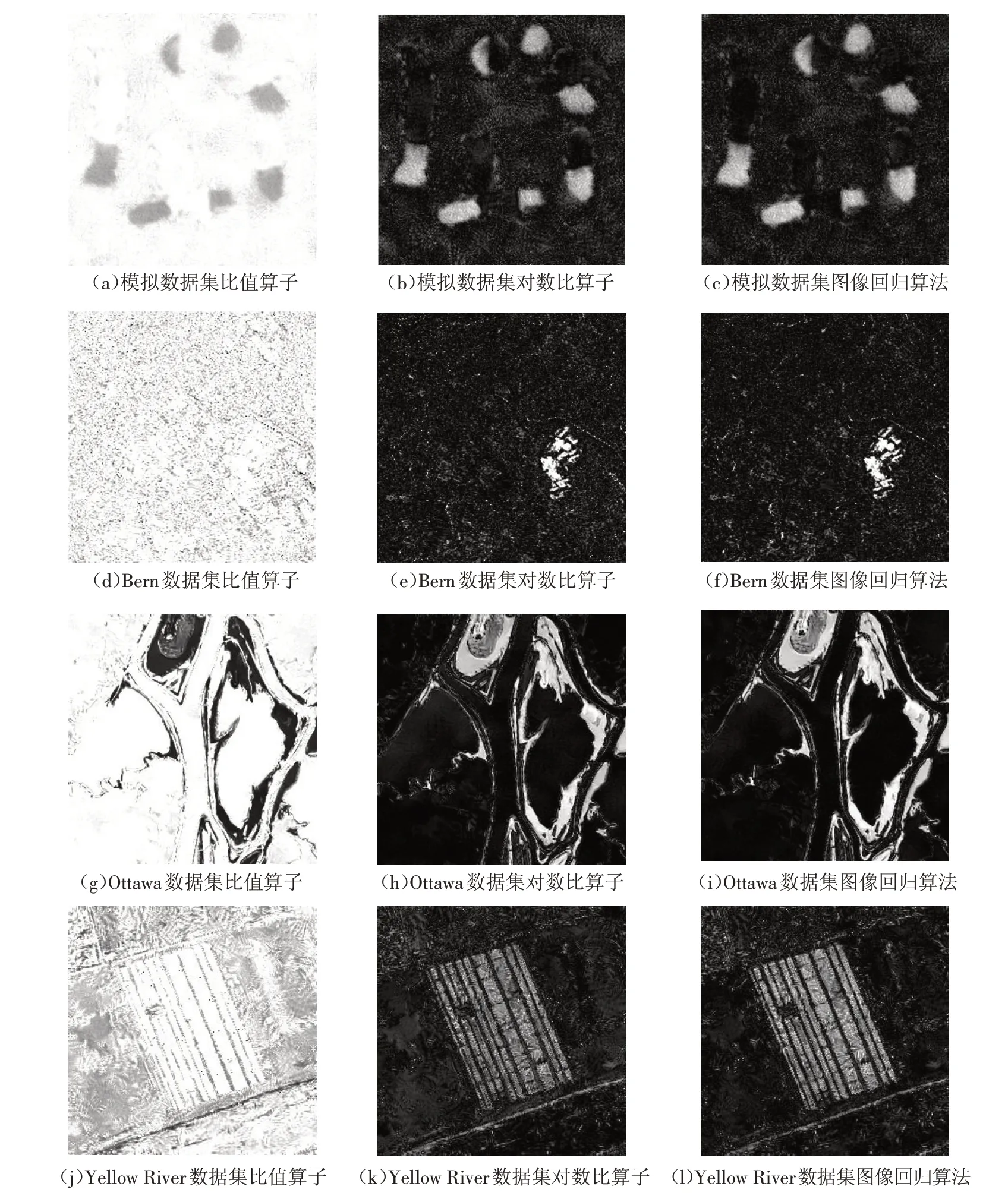
图7 四组SAR图像数据集分别采用比值算子、对数比算子以及图像回归算法构造的差异图Fig.7 DI of the four data sets based on the three different methods：Ratio，Log-ratio，IR

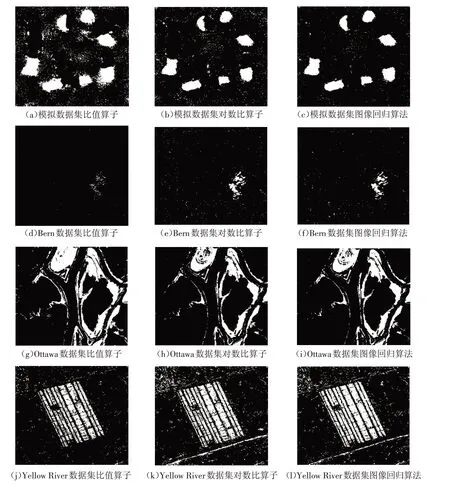
图8 比值算子、对数比算子以及图像回归算法分别对四组SAR图像构造的差异图分别使用FCM聚类算法得到的最终变化检测结果Fig.8 Change detection results obtained by the FCM clustering algorithm for difference graphs of four data sets based on the three different methods：Ratio，Log-ratio，IR and FCM clustering algorithm

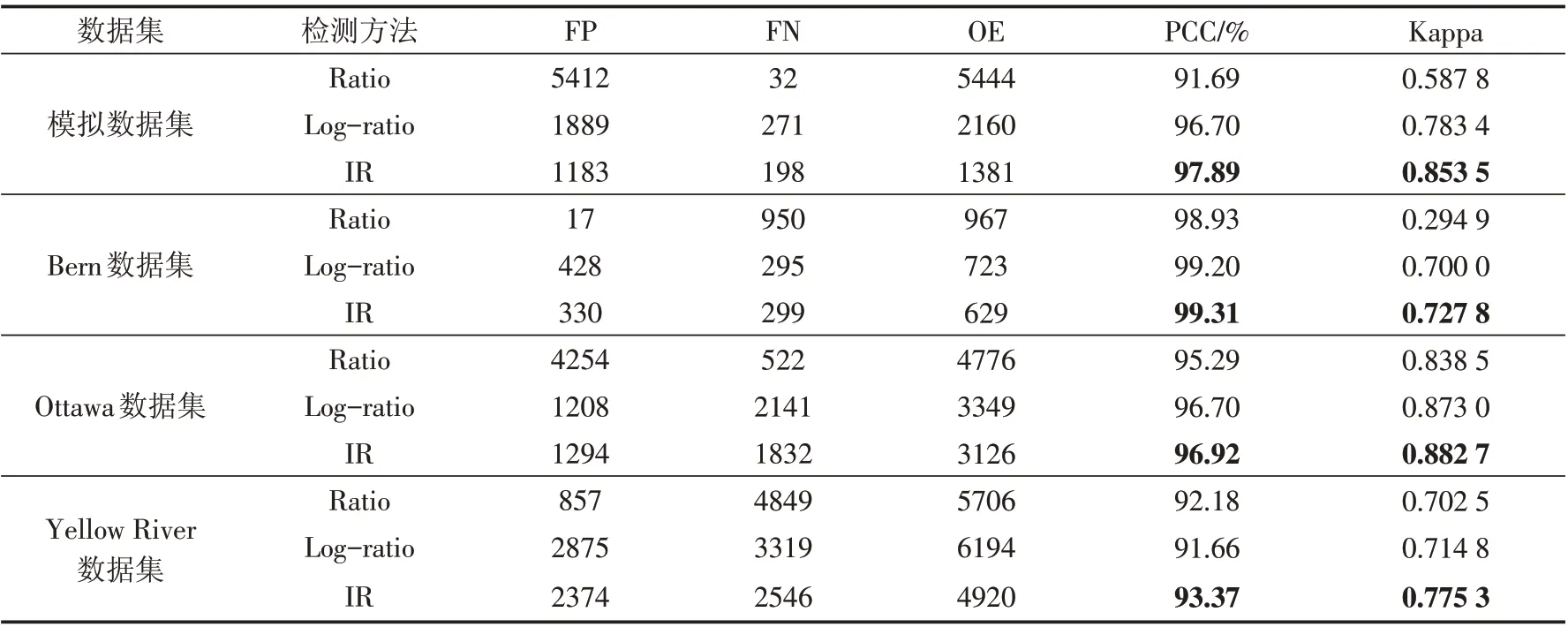
表1 对三种方法构造的差异图分别使用FCM聚类算法得到的变化检测结果指标比较Tab.1 Comparison of the change detection results by using different methods and FCM clustering algorithm

3 结语

本文提出了一种基于图像回归的差异图构造方法，该方法主要思想是利用线性回归模型对变化后的图像进行重构.先通过对SAR图像数据集进行预检测获取样本点；然后利用变化前图像信息和线性回归模型对变化后图像进行重构；最后利用对数比算子度量重构图像与变化后图像之间的差异获得差异图，并利用FCM对差异图进行聚类分析得到最终的变化检测结果.将图像回归法与比值法、对数比值法构造差异图进行了对比实验，结果表明，基于图像回归的差异图构造方法在一定程度上提高了变化检测算法的性能.