Weniger变换在求非谐振子无穷耦合极限中的应用
姚清照, 贺黎明
(华东理工大学物理系,上海 200237)
对许多数学和物理问题进行计算时,经常会得到无穷级数结果。对于一些收敛缓慢或发散的无穷级数,需要借助特殊的级数计算方法,才能得到有意义的数值结果。近几十年来,非线性数列变换的方法[1]逐渐发展,该方法能有效地加速收敛级数以及求发散级数的和,并在微扰论求解物理体系问题中得到越来越广泛的应用。
非谐振子是一种重要的物理系统,可以作为晶体振动的简化模型,且在量子场论中也有广泛的应用。在用微扰论求解强耦合条件下非谐振子基态能量本征值时,得到的解是发散级数,要计算无穷耦合极限必须借助特殊的求级数和技巧。非线性数列变换方法正适合解决这类问题。发散的级数经过非线性数列变换处理后,可以得到数学性质更好的新数列,从而收敛到一个广义的极限值(通常称为反极限),此过程即为发散级数求和。现有的求解非谐振子问题的工作多数采用浮点计算[2],所得结果的精度都受到舍入误差的限制。
本文使用Weniger变换求非谐振子基态微扰级数和,从而计算四阶,六阶和八阶无穷耦合极限。同时利用计算机代数系统Maple的代数计算功能,进行完全有理化的计算,克服了舍入误差的限制。针对在计算机代数系统中进行高阶Weniger变换时遇到的内存迅速消耗问题,本文采用微扰级数系数分离计算的策略,并压缩非线性数列变换程序中关键数组的维数,通过这两种优化极大地解决了内存溢出的问题,得到精度极高的无穷耦合极限近似值。
1 非谐振子及重整化
谐振子是一种有精确解的物理模型,在许多物理问题中有广泛的应用。当它处于外场中时,就会产生附加的作用项,此时的体系称为非谐振子。非谐振子体系没有严格解,只能作近似处理,可以把非谐振子体系的哈密顿量写成[3]


为了解决微扰级数发散速度过快的问题,对微扰级数进行重整化处理可以显著地降低发散速度,如Arteca等[5]对重整化各种算法进行比较和总结。其中一种方式由Weniger得到[3],通过引入一对共轭变数:
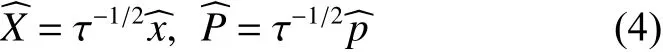
得到了重整化后的哈密顿量
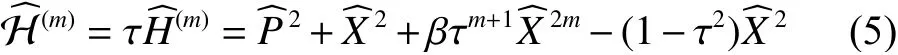
进一步根据变分法并结合其实际的物理意义,就可以得到一个表达式将待定常量 τ 和耦合常数β联系起来:
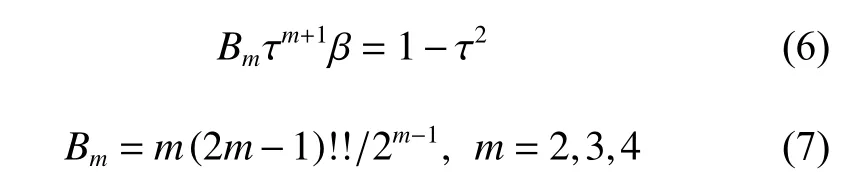
m为2,3,4时分别对应B2=3 ,B3=45/4 ,B4=105/2。引入重整化耦合常数

可得到原哈密顿量中的原耦合常数 β 关于重整化后的耦合常数 κ 的表达式

依照式(9)可以得到不同非谐振子体系中耦合常数变换的表达式。原耦合常数 β 符合物理意义的定义域是一个半无穷区间 [ 0,∞) 。利用式(9),重整化可以将关于 β 的半无穷区间投影到关于 κ 的左闭右开单位区间 [ 0,1) 上。重整化方法将耦合常数的定义域重新构造成更小的区间,从而使发散微扰级数的求和变得相对简易,在耦合常数 β 值较大时重整化的优势将尤为明显。
本文将参量Bm的定义式(7)和新旧耦合常数间的关系式(9)代入重整化哈密顿量表达式中得到更简约的形式

其中


将式(10)带入Schrödinger方程则能得到重整化Schrödinger方程:

易看出重整化能量本征值(κ) 已由下标R标记出来,此时耦合常数也变为 κ 。基态下非谐振子能量本征值
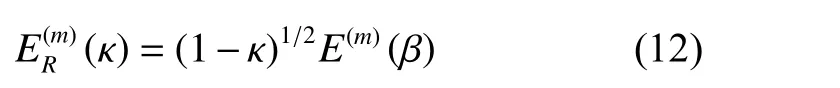
关于 κ 的级数展开为:
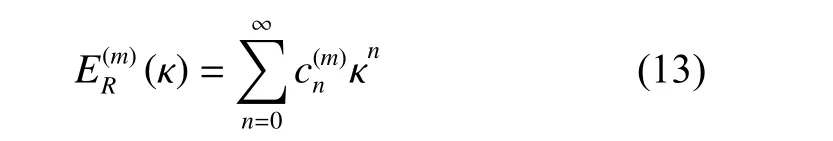


就可以计算出无穷耦合极限km,km的计算式为式(17)。

其中参数Bm的计算式已由式(7)给出。无穷耦合极限km计算所涉及的展开级数是重整化级数中最困难的问题,而有限场强 β 对应耦合常数 κ ∈[0,1) ,此时重整化微扰级数发散速度相对缓慢,求级数和更为容易。因此,计算无穷耦合极限的工作,对于其他任意有限场强中求解本征值问题有很好的借鉴意义。
我们已知的最好的四阶、六阶和八阶非谐振子的无穷耦合极限结果是由Vinette等[8]通过重整化内投法(Renormalized inner projection)分别计算到小数点后62、33和21位小数。
2 非线性数列变换
非线性数列变换是一种加速级数收敛或求发散级数和的方法。根据大量的实际计算结果[9-10]可知,Levin变换是效率最高且适用范围最广的一种非线性数列变换。然而,在求非谐振子基态本征值微扰级数和时,Levin变换所得结果出现了发散的现象,不能计算出高精度的非谐振子无穷耦合极限。考虑到Levin变换通常有很强的求发散级数和的能力,Weniger在保留Levin变换优点的基础上提出了Weniger变换[1],该变换是以模型数列式(18)为基础构造的。

其中 ωn为余项估计,待定参数 ζ =1 ,且式中采用了Pochhammer符号

如果式(18)中的余项估计 ωn与部分和之积能作为实际余项rn准确的近似式,那么Weniger变换就能给出高精度的极限s(发散级数的和通常称为反极限)近似值。利用差分算符的方法可以得到Weniger变换的定义式为
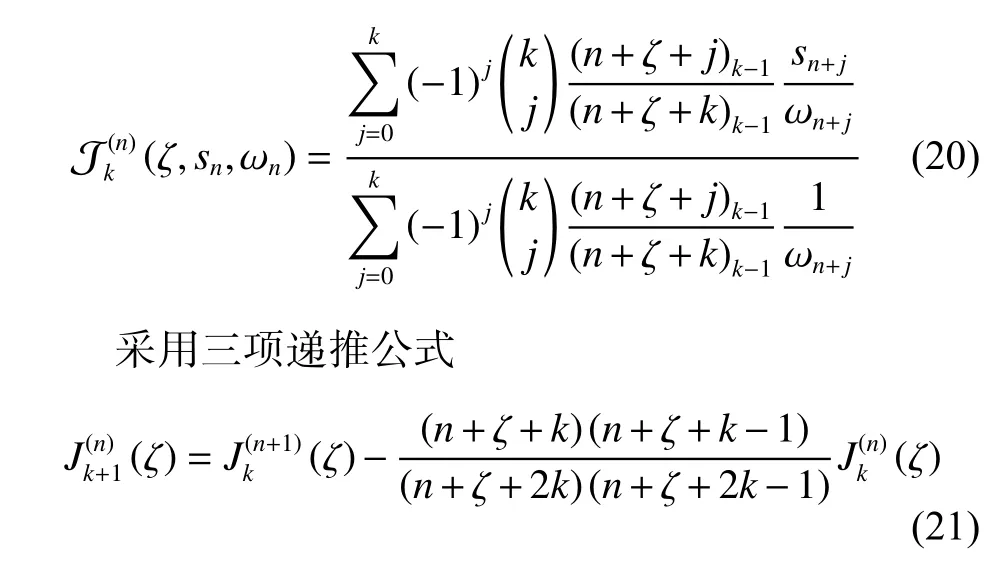
计算式(20)可以看出递推公式能在Weniger表中形成一个三角形。式中的元素表示定义式(20)中分子或分母的计算值,如果用上标n表示行标,下标k表示列标,则可以构成一个呈左上三角形的二维矩阵:

其中变换阶k的最高阶km=l。
式(22)第1列中的元素是迭代计算过程的起始值,右边各列的元素都可以通过三项递推式(21)逐列计算得到。如果用式(23)作为起始值

通过递推式(21)能得到Weniger变换式(20)的分子。如果用式(24)作为起始值

则计算所得为Weniger变换式(20)的分母。将对应Weniger分子和分母表中相同位置的元素相除,则能得到Weniger变换 J 结果表,其同式(22)一样是一个左上三角矩阵。
文献[11]指出,四阶、六阶和八阶非谐振子重整化微扰级数属于各项正负交替的Stieltjes级数。因此,用余项估计 ωn=∆sn=an+1能有效地逼近实际余项,对应得到

在实际计算过程中,通常以待变数列部分和元素构成的有限子集 {s1,s2,···sl} 作为输入数据,我们称这个子集为待变序列。理论上,变换阶k增加时产生的结果更精确。然而,在实际计算中,变换结果的精度开始时随着变换阶k的增加而变高,在某一最佳变换阶得到有效位数最高的结果后,后续的结果就会逐渐变差。因此我们需要改变待变序列的长度l,进行多次数列变换,进一步观察收敛的效果。
本文借助计算机代数系统Maple实现了完全有理化的计算,数据在计算过程始终为有理数格式,所以不会产生舍入误差,然而,代价是单个数据的表示和计算会消耗更多的内存和机时。随着计算过程向高阶变换进行,Maple会消耗越来越多的内存,因此很容易发生内存溢出的问题。
针对内存溢出的问题,本文采用了两种优化方案。首先,根据式(14)可以看出,在计算微扰级数系数时需要先计算辅助参数,且随着n增大辅助参数的个数线性增加。将计算微扰级数系数过程和数列变换迭代过程程序分开,并把微扰级数系数输出到txt文件中,在计算变换结果前再以有理数格式读入,这样则能节省出可观的内存。其次,Weniger变换结果表是类似式(22)的三角形二维数组,如果把三项递推公式(21)计算的结果覆盖在原参数名上,则能将二维数组压缩成一维数组,节省出中间迭代过程消耗的内存。在迭代过程中,每列底部的数据会保持不变,因此我们最后所得一维数组正好是k=0,1,···,km阶变换的结果,对应于式(22)矩阵中的反对角矩阵元。
3 计算结果与分析

3.1 四阶非谐振子


表1 四阶非谐振子微扰级数系数 c (n2) 及其部分和数列∑(n2)Table 1 Coefficients c (n2) and partial sums ∑ (n2) of perturbation series for quartic anharmonic oscillator

表2 四阶非谐振子微扰级数系数 及其部分和数列的浮点数计算结果Table 2Floating-type coefficients and partial sums of perturbation series for quartic anharmonic oscillator

表2 四阶非谐振子微扰级数系数 及其部分和数列的浮点数计算结果Table 2Floating-type coefficients and partial sums of perturbation series for quartic anharmonic oscillator
n c(2)n∑(2)n 1.000 000 000 0 1.000 000 000 0 1−0.250 000 000 0 0.750 000 000 0 2−0.020 833 333 3 0.729 166 666 7 3 0.015 625 000 0 0.744 791 666 7 4−0.028 609 664 4 0.716 182 002 3 5 0.065 764 250 6 0.781 946 252 9 6−0.183 697 107 9 0.598 249 145 1 7 0.604 032 383 0 1.202 281 528 0 8−2.285 197 581 9 −1.082 916 053 8 9 9.777 776 663 8 8.694 860 609 9 10 −46.687 745 963 8 −37.992 885 353 9 11 246.122 512 752 4 208.129 627 398 5 0

计算结果列于表3第2列。由表3可以看出,无穷耦合极限k2的吻合的有效位数开始时随着变换阶k的增加而变多,到了第7阶后有效位数又开始减少。
为了更定量且直观地考察Weniger变换过程的收敛情况,定义:
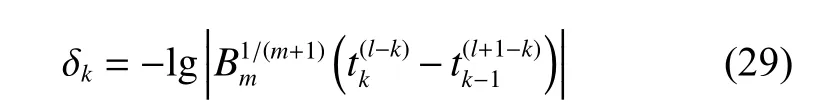
δk表示相邻两次迭代结果的符合程度,大致对应于两个十进制浮点数取得一致的位数。不同变换阶k时计算结果的 δk不同,通常 δk值越大对应的近似值精度也就越高。从表3可以看出,通过数列变换的方法,我们从发散级数所包含的数学信息中提取出了收敛的有限值,原本发散的微扰级数因此获得了物理意义。 δk先随着变换阶k的增加而不断增加,在最佳变换阶k=7 时最大,然后转为变小。因此最高精度为 ∆10=6.947 ,对应收敛到7位有效数字的结果为k2=1.060361 。
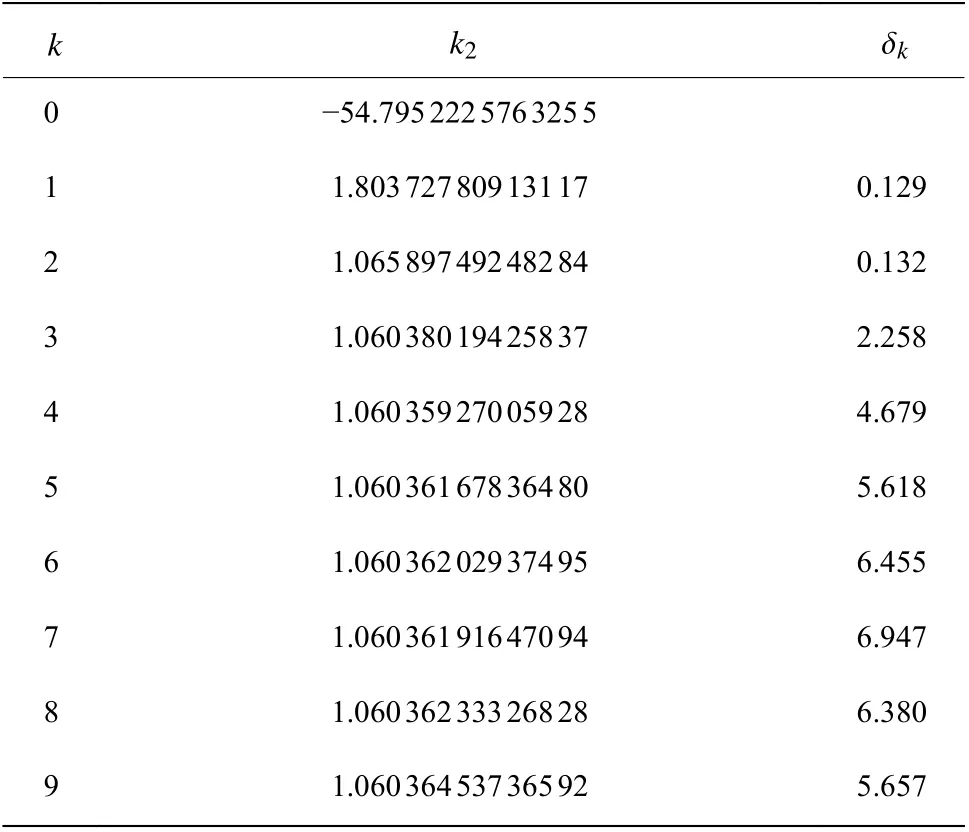
表3 序列(27)Weniger变换的结果Table 3 Numerical results of Weniger transformation for the string (27)

为了更深入地考查Weniger变换求四阶非谐振子微扰级数和的能力,按照与l=100 时相同的方法,依次计算了待变序列长度l=200,300,···,800 的Weniger变换结果,整理成表5。计算Weniger变换所选择的待变序列越长,所需要的微扰级数系数越多,可以进行更高阶的变换,给出的结果精度越高,最高精度 ∆l=105.646 ,是由待变序列长度l=800变换到k=756 得到k2为1.060 362 090 484 182 899 647 046 016 692 663 545 515 208 728 528 977 933 216 245 241 695 943 563 044 344 421 126 896 299 134 671703 510 546,这比现有的最准确的内投法结果[8]还要高出大约43位有效数字。
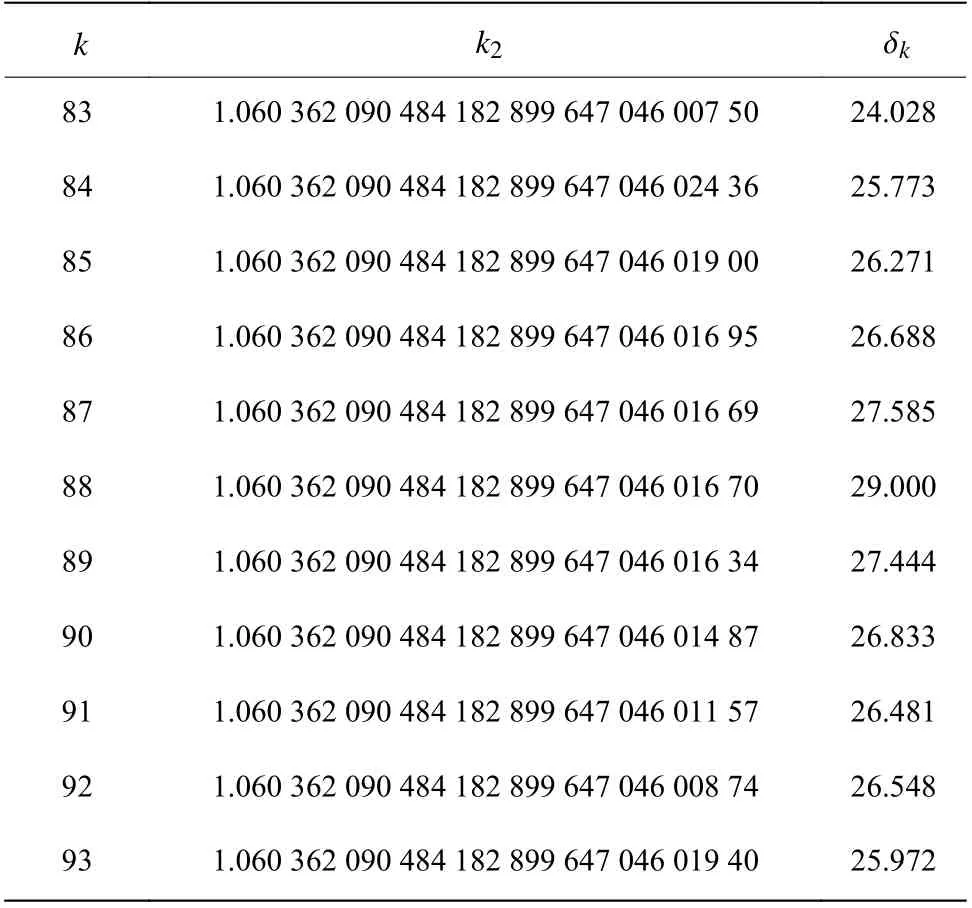
表4 l为100时Weniger变换的结果Table 4 Numerical results of Weniger transformation for l=100
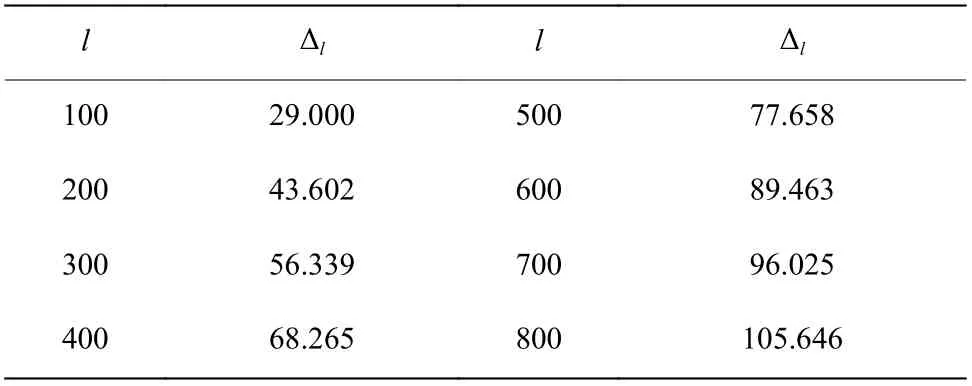
表5 对不同长度l待变序列式(27)进行Weniger变换得到无穷耦合极限 k2 的有效位数∆lTable 5 Number of decimal significant digits ∆l of approximations of infinite coupling limit k2 given by Weniger transformation for various lengths of strings(27)
本文使用图形软件Origin,以拟合函数∆l=a+bl+cl2对表5中的 ∆l和l数据进行二次多项式拟合,可以得到图1。其中,截距a=14.56107± 1 .31521 ,一阶系数b=0.15349±0.00671 ,二阶系数c=−5.0519×10−5±7.27312×10−6,残 差 平 方 和 为 4 .44345 ,R2=0.9991 。从图1可以看出吻合的有效数字位数 ∆l关于待变序列长度l线性增加,这说明我们只需增加待变序列长度就可以计算出有效数字更多的四阶非谐振子耦合极限k2。
3.2 六阶非谐振子
六阶非谐振子微扰级数系数增长更迅速,文献[3]中,在指标n相同时微扰系数相对于四阶非谐振子的系数更大,微扰级数发散更快。因此待变序列式(27)的长度相同时,六阶非谐振子的计算量更大。依照四阶非谐振子的情形,我们使用Weniger变
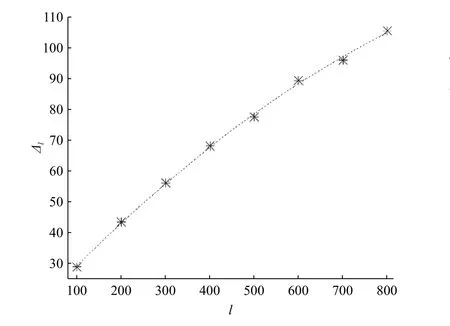
图1 四阶非谐振子无穷耦合极限 k2 近似值的有效位数∆l 与待变序列式(27)长度 l 之间的关系Fig. 1 Relationship between the significant digit ∆l of the approximation k2 of the infinite coupling limit of the quartic nonharmonic oscillator and the length l of the string (27)

3.3 八阶非谐振子
以长度l=100 待变序列式(27)经过Weniger变换所得八阶非谐振子无穷耦合极限k4,结果如表8所示。结合表4、表6和表8可得,四阶、六阶和八阶非谐振子在待变序列长度l=100 时,有效位数∆l逐渐减少,依次为29,11和6。对于同样长度的待变序列,由于级数的发散特性更加明显,m值大阶数高的非谐振子需要消耗更大的计算量和内存空间,却只能得到更差的结果。
我们依次对长度l=200,300,···,900 的待变序列式(27)进行了Weniger变换。在待变序列长度l>500后,出现了服务器内存溢出的问题。我们通过优化数组结构等方法,成功计算出了待变序列长度l=900 时八阶非谐振子的无穷耦合极限,结果见表9。从表9可以看出变换阶k=890 时得到最高有效位数 ∆900= 1 3.488 ,即第890阶变换结果和第889阶变换结果大致有14位吻合的有效数字,这时已到达我们计算资源的极限。
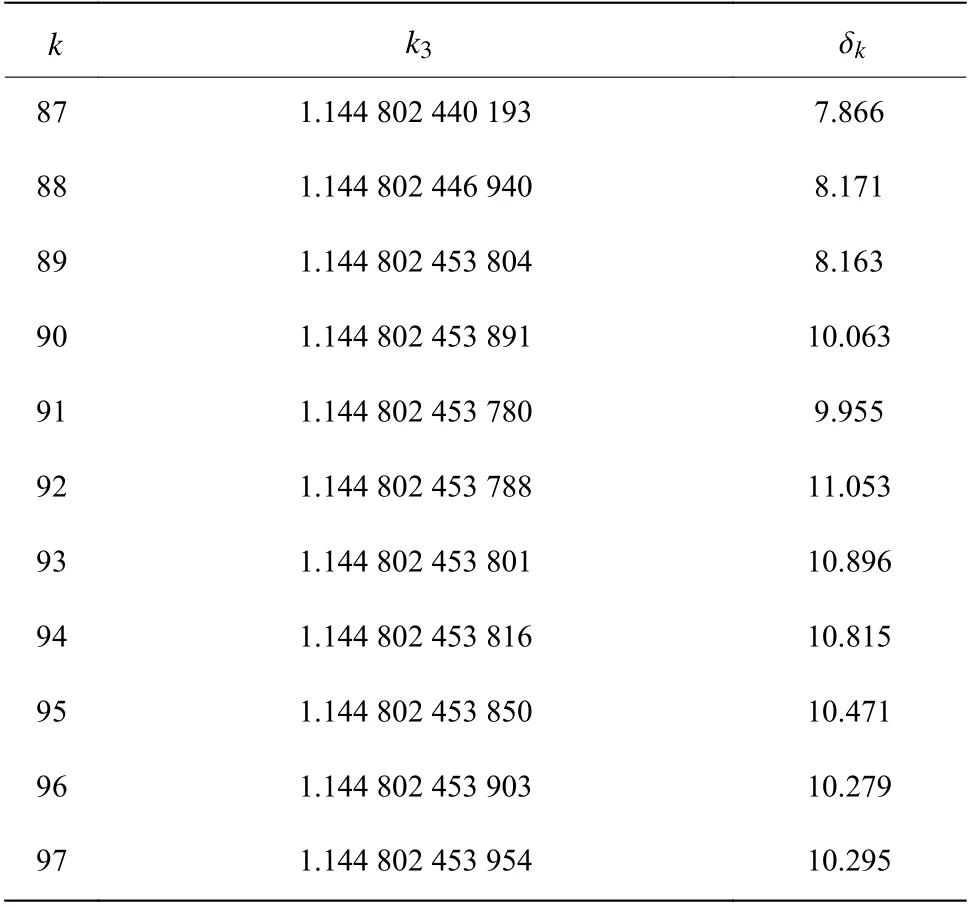
表6 l =100 时Weniger变换的结果Table 6 Numerical results of Weniger transformation for l=100

表7 l =1000 时Weniger变换的结果Table 7 Numerical results of Weniger transformation for l=1000
4 结论与展望

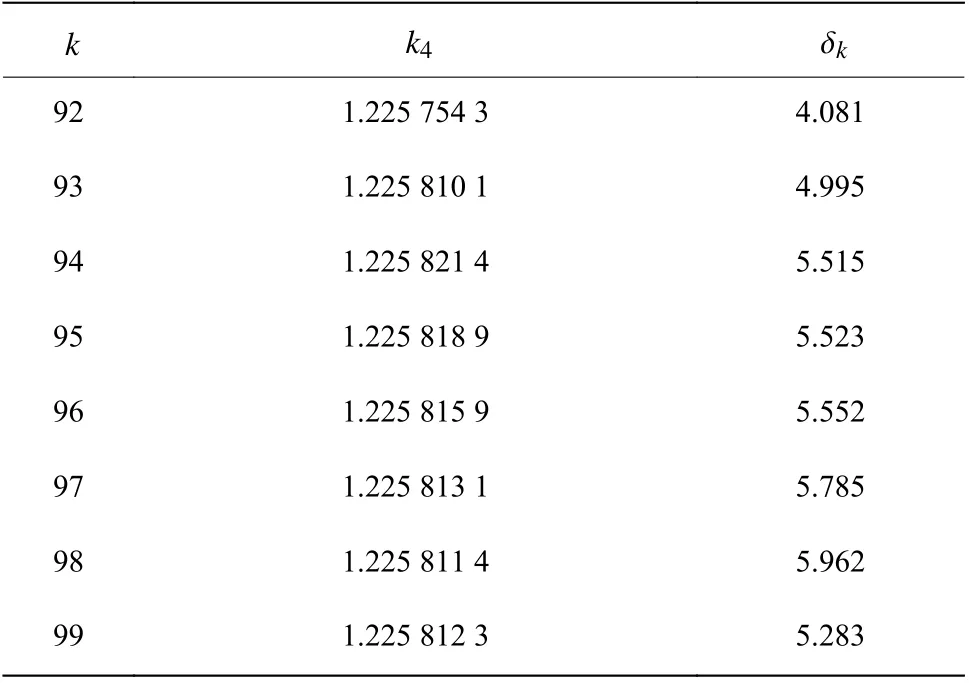
表8 l =100 时Weniger变换的结果Table 8 Numerical results of Weniger transformation for l=100

表9 l =900 时Weniger变换的结果Table 9 Numerical results of Weniger transformation for l=900

在Maple计算过程中,每个系数是巨大的有理分数形式,不仅占据了大量内存,还会明显增加计算量。六阶和八阶非谐振子微扰级数系数比四阶的增长更快,在进行Weniger变换时需要更多的内存和计算量,计算无穷耦合极限也就更为困难。我们计算无穷耦合极限k3和k4时遇到了服务器内存溢出的问题,为此我们改进了Weniger的程序数组结构,将二维数组通过覆盖的编程技巧将其压缩为一维数组。一维数组的优化方案节省了巨大的内存,这个改进使我们可以计算出比Weniger更准确的结果,不然的话,即使是在我们现有的计算条件下也很难得出比Weniger[3]更好的计算结果。此外,由公式(14)可以看出,将计算微扰级数系数c(nm)部分的程序分离出迭代的变换过程,也能节省出大量保存辅助参数时被浪费的内存。微扰级数的微扰阶越高,待变序列长度越长,这种优化方案的优势就更显著。表10中汇总了我们优化方案的计算结果和其他方法所得结果的比较。
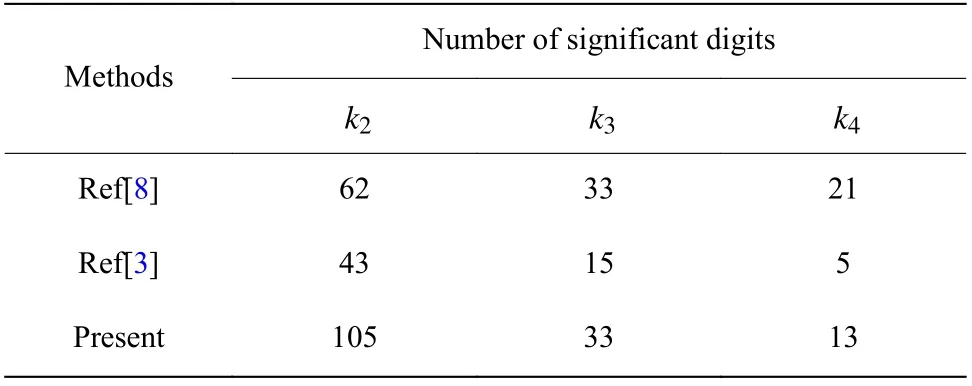
表10 四阶、六阶和八阶无穷耦合极限计算结果与其他方法的比较Table 10 Comparison between present numerical results of quartic, sextic and octic infinite coupling limits and other methods
如果有更多的计算机内存资源,则可以计算出更多位数的无穷耦合极限。而且当内存足够充足时,若使用Maple的并行运算功能,将极大地提升计算速度,节省CPU时间。因此内存资源是更为关键因素。
微扰论是求解许多物理体系的常用近似计算方法。实际计算得到的无穷级数为缓慢收敛和发散的情况也是非常普遍的。于是,通过非线性数列变换改善无穷级数的收敛性质具有普遍的实际意义[12]。

