基于表皮效应的单井循环地下换热系统地下水渗流方程的统一分析

宋 伟，王 浩，郑昌金，刘远周

（北方工业大学 土木工程学院，北京100144）

0 前言

地下水源热泵系统可以利用地热资源，其中单井循环地下换热系统是地下水源热泵系统的一种形式。在取热量相同的情况下，与地下埋管换热器相比，单井循环地下换热系统所需的打井数量较少，初投资较低，从而得到广泛应用[1]，[2]。目前，单井循环地下换热系统主要有循环单井、抽灌同井和填砾抽灌同井[3]。循环单井是在基岩上打井，且为裸井，回水主要与井壁换热，少部分回水流经基岩含水层后直接进入抽水区。抽灌同井和填砾抽灌同井的相同点：①均在井孔内设置隔板，用于防止回水与抽水相互掺混，减少热贯通效应；②二者的回水均进入含水层，与含水层中的原水和固体骨架换热后进入抽水区。不同点为填砾抽灌同井井壁周围回填孔隙率较大的砾石，这层砾石区有利于回水进入含水层[4]。

针对3种热源井的地下水运动规律已有研究。倪龙建立了非稳态、有越流的循环单井地下水渗流方程，武强在倪龙研究的基础上，建立了含有蓄能颗粒与无储能颗粒的循环单井地下水渗流数学模型[5]～[7]。李旻建立了无越流、非稳态条件下抽灌同井的地下水渗流方程，武强在李旻研究的基础上添加越流项。王玉林在武强研究的基础上，分析了抽水与回水周期性变化和回灌率对地下水流动的影响[8]～[11]。由于不同热源井建立的地下水渗流方程不同，且边界条件较为复杂，因而地下水渗流数学模型难以应用于实际工程，因此，须要建立3种热源井统一的理论模型。大多学者仅考虑渗透系数各向异性，未得到渗透系数各向异性对地下水流动的影响。填砾抽灌同井的填砾区与表皮效应理论中的表皮类似。目前，已有学者研究了表皮效应对地下水流动的影响，在实际生产中为了减小表皮效应对开采地下水的影响，假设有效井孔半径大于实际井孔半径，并在此基础上建立了数学模型[12]。王玉林发现井壁处的表皮效应系数为非均匀分布，将含水层沿竖直方向分割成多个小含水层，每个小含水层的表皮效应系数均匀分布，假设含水层的表皮效应系数按某种规律分布，建立承压含水层的稳态渗流数学模型，通过模拟发现，表皮效应系数越小，含水层的降深和抽水流量越大[13]，[14]。

本文利用表皮效应统一3种热源井近井壁处的渗透系数，得到渗透系数转换关系式。本文建立填砾抽灌同井地下水渗流方程和边界条件，获得地下水渗流方程的解析解，考虑渗透系数各向异性对地下水流动的影响；通过渗透系数转换关系式，本文得到抽灌同井和循环单井地下水渗流方程的解析解。本文编制计算程序求解填砾抽灌同井地下水渗流方程的数值解。通过对填砾抽灌同井的地下水渗流方程的解析解与数值解进行比较，验证了填砾抽灌同井的地下水渗流方程的数值解的合理性。

1 统一热源井井壁处渗透系数

1.1 表皮效应

在实际开发地下水资源或开采石油时，钻井、完井和生产实践活动减小了井壁处的渗透系数。井壁处渗透系数改变的区域称为“表皮”。图1为表皮效应示意图。

图1 表皮效应示意图Fig.1 Schematic diagram of skin effect

图中曲线AB为降深曲线，在工程实践中，井筒内压力点为E1，理论推导的压力点为E，为解释实际与理论的压力差ΔP，本文引入表皮效应系数。表皮效应系数的计算式为[15]

式中：S为表皮效应系数；K为含水层的渗透系数，m/s；Ks为表皮的渗透系数，m/s；rw为井壁半径，m；rc为表皮层影响半径，m。

当表皮渗透系数小于含水层的渗透系数时，表皮效应为正表皮效应；当表皮渗透系数大于含水层的渗透系数时，表皮效应为负表皮效应。

1.2 3种热源井渗透系数

研究人员已对3种热源井井壁处的渗透系数进行了详细地研究，并得到了3种热源井井壁处的渗透系数数学模型，具体如下。

①抽灌同井

M K Hubbert在进行达西实验的过程中发现，流体流过同一种多孔介质时，抽灌同井条件下，井壁处的渗透系数与流体的运动粘滞系数成反比，与多孔介质平均直径的平方成正比，经过数学推导得到抽灌同井渗透系数k1的表达式为[16]

式中：D1为抽灌同井条件下，井壁处颗粒的平均直径，m；C为固体骨架结构的比例常数，C与颗粒的大小、分布、球度、密实程度等有关；g为重力加速度，m/s2；v为液体的运动粘滞系数，m2/s。

②填砾抽灌同井

填砾抽灌同井的填砾区是由粒径较大的砾石组成，填粒区是多孔介质，多孔介质的孔隙较多且孔隙的直径较大，基于此假设多孔介质中的孔隙为一束等长度的毛细管，利用N-S方程和Kozeny-Carman方程联立求解，得到填砾抽灌同井条件下，井壁处渗透系数k2的表达式为[17]

式中：ρ为流体的密度，kg/m3；D2为砾石的平均直径，m；μ为流体的动力粘滞系数，N·s/m2；n为孔隙率。

③循环单井

陈崇希通过研究发现，水平井的回水区分为两部分：一部分为圆形管道，另一部分为含水层。圆形管道的渗透系数与管道内流体的流动状态有关，当圆形管道内流体的流动状态为层流时，圆形管道的渗透系数可以由文献[18]进行推导。

圆形管道的水头损失Δh的计算式为

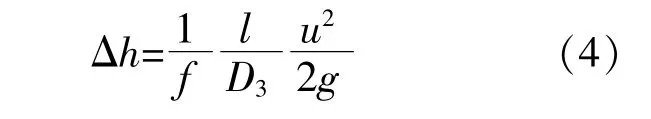
式中：f为管壁的摩擦系数；l为管道长度，m；D3为管道直径，m；u为管道内流体的平均流速，m/s。

f的计算式为

式中：Re为雷诺数。

Re的计算式为

v的计算式为

圆形管道的渗流速度V的计算式为

当介质为水时，设定孔隙率n为1，则V=u，并带入式（4）～（7）化简整理得到：

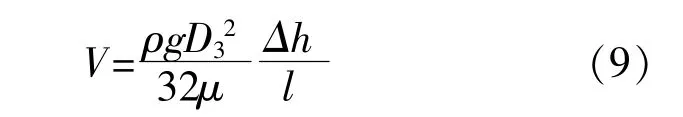
综上可得，循环单井的渗透系数k3为

1.3 统一渗透系数

3种热源井示意图如图2所示。

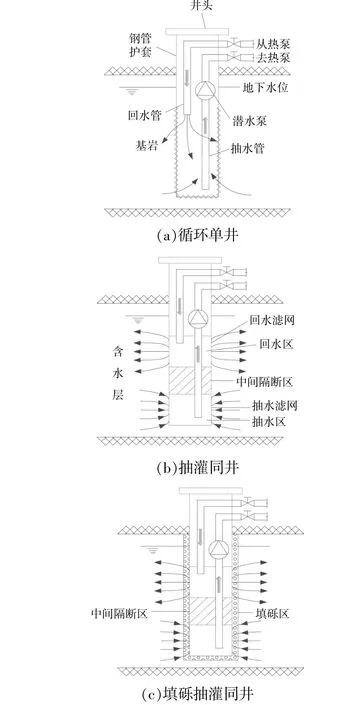
图2 3种热源井示意图Fig.2 Schematic diagram of three thermalwells

由于3种热源井的结构不同，导致3种热源井井壁处的渗透系数不同，本文将3种热源井井壁周围区域放大，得到3种热源井表皮效应，具体如图3所示。

图3 3种热源井表皮效应Fig.3 Skin effect of three thermalwells

假设抽灌同井、循环单井存在与填砾区类似的区域（回填区），抽灌同井的回填物与含水层的物理性质相同，循环单井的回填物为水。根据渗流力学中的表皮效应，将3种热源井的回填区类比为表皮，由此对3种热源井的渗透系数进行统一。基于表皮效应理论，将抽灌同井条件下井壁的渗透系数等效于填砾抽灌同井和循环单井条件下井壁的渗透系数。由于抽灌同井回填区材料与含水层的物理性质相同，即：

将式（11）带入式（1）中，得到S=0。由于填砾抽灌同井回填区材料为粒径较大的砾石，因此，回填区的渗透系数大于含水层的渗透系数，即S＜0，rw＜rc。将S＜0，rw＜rc带入式（1）得到k2/K＞1，将k2/K＞1带入式（2），（3），（11）整理得到：

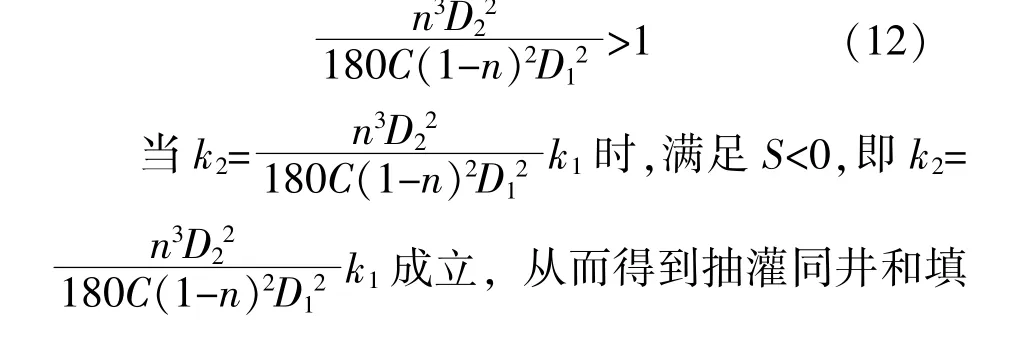
2 地下水渗流方程的求解

2.1 地下水渗流方程

填砾抽灌同井结构如图4所示。填砾抽灌同井具有井轴对称的特点，填砾抽灌同井的井轴为纵轴，含水层的底部为横轴，含水层上半部分为回水区，含水层下半部分为抽水区，回水经回水滤网进入回水区，含水层原水从抽水区进入抽水滤网，抽水与回水在含水层同一径向不同深度处发生。

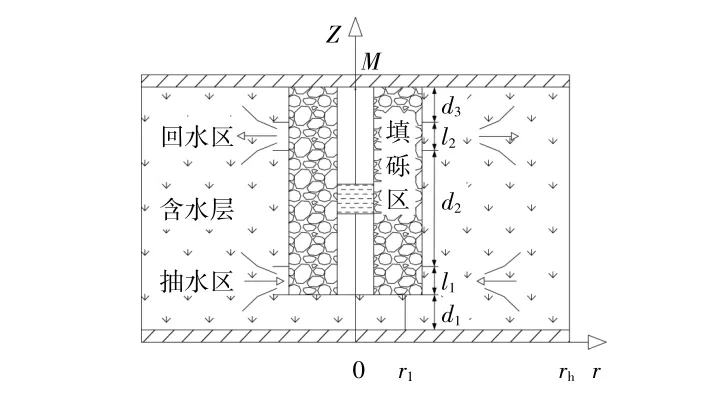
图4 填砾抽灌同井结构图Fig.4 Structure diagram of FECSCW

含水层应满足的假设条件、渗流方程及边界条件如下。

①假设条件

假设含水层为无越流承压含水层，当含水层的压力下降时，含水层立刻弹性释水；含水层为均质、各向异性的物质，主渗透方向为水平方向和竖直方向，含水层厚度始终不变，含水层的侧向无限延伸；流体在含水层中的流动符合达西定律；回灌和抽水流量相等，且抽、回水量在抽、回水滤网处均匀分布；当系统稳定运行时，地下水流动处于稳态渗流。

②渗流方程及边界条件

基于上述假设条件，得到承压含水层中渗流微分方程为

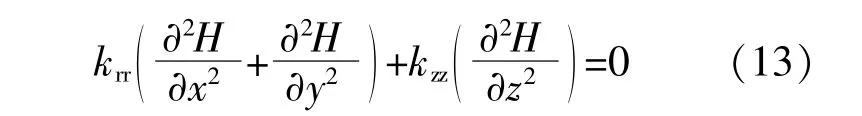
式中：H为地下水的压力，kPa；krr为含水层水平方向的渗透系数，m/s；kzz为含水层竖直方向的渗透系数，m/s。

边界条件的表达式为

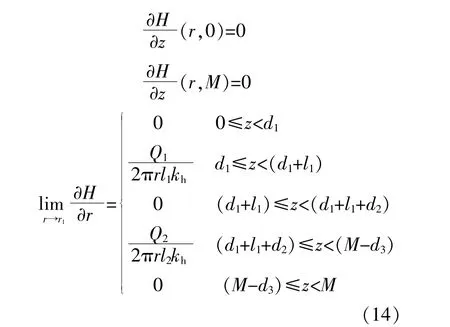
式中：r1为井中心与井壁之间的距离，m；r为井中心距含水层内任一点的半径，m；kh为填砾抽灌同井壁面处的渗透系数，m/s；Q1为回水流量，m3/s；Q2为抽水流量，m3/s；M为含水层的厚度，m；d1为抽水滤网下边缘与含水层底部之间的距离，m；l1为抽水滤网长度，m；l2为回水滤网长度，m；d2为回水滤网下边缘与抽水滤网上边缘之间的距离，m；d3为回水滤网上边缘与含水层顶部之间的距离，m。

2.2 解析解

边界条件的表达式为

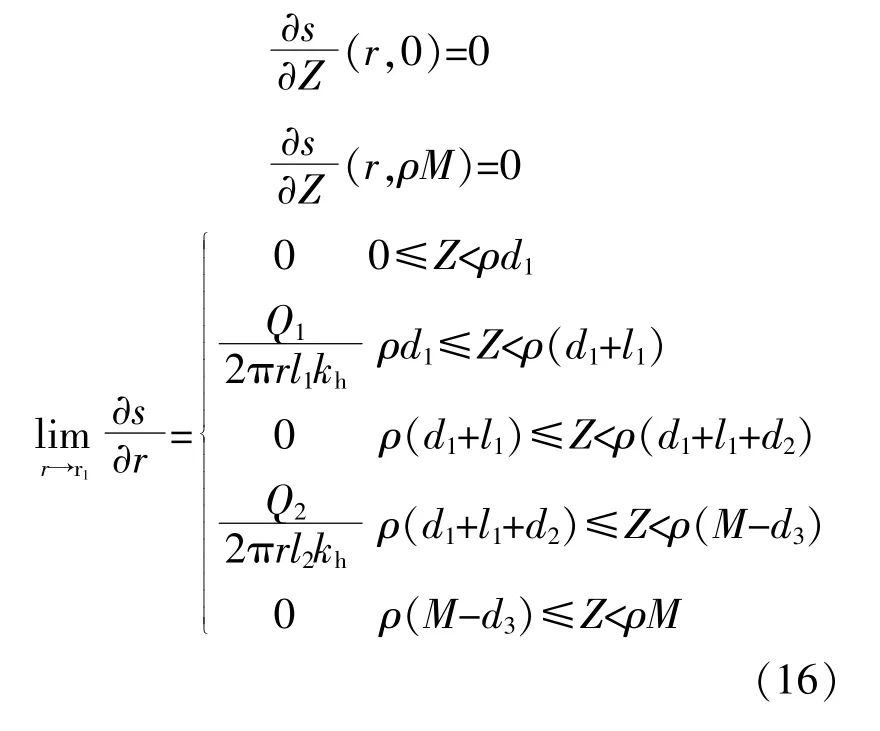
利用分离变数法对式（15）进行处理，并将式（16）按余弦级数展开，得到填砾抽灌同井的降深方程。

式中：K0（nπr/ρM），K1（nπr1/ρM）为第二类虚宗量贝塞尔函数；w为填砾抽灌同井的结构计算变量。

通过3种热源井井壁处的渗透系数关系式，本文得到抽灌同井与循环单井的降深方程。

填砾抽灌同井的结构计算变量的表达式为

2.3 数值解

图4中填砾抽灌同井关于z轴对称，因此只取填砾抽灌同井和含水层的一半进行研究，并利用外节点法对井壁外含水层区域进行网格划分。为了与地下水渗流方程的解析解进行比较，本文假设渗透系数各项同性，即krr=kzz，ρ=1，Z=z，通过有限差分法对式（15）进行离散，得到网格中心点、回水滤网处、抽水滤网处、上顶板、下顶板处的地下水压力计算式分别为

式中：i为网格的纵坐标；i+1为i上方相邻纵坐标；i-1为i下方相邻纵坐标；j为网格的横坐标；j+1为j上方相邻横坐标；j-1为j下方相邻横坐标；H（i，j）为网格的地下水压力，kPa；ri为网格的半径，m；Δr为网格的宽度，m；Δz为网格的高度，m。

网格的计算程序步骤：①设置网格的初始值及迭代计算的收敛条件（2次计算结果的差值小于10-6）；②进行网格的迭代计算，当网格的数值满足收敛条件后停止计算。

3 模型验证

引用参考文献[22]中填砾抽灌同井的数据，表1为填砾抽灌同井参数取值。本文通过地下水渗流方程的解析解验证地下水渗流方程的数值解，具体步骤：①地下水渗流方程的解析解与数值解的地下水压力分布趋势是否相同；②地下水渗流方程的解析解选取3个不同位置的地下水压力值，地下水渗流方程的数值解同样选取相同位置的地下水压力值，解析解的地下水压力值与数值解的地下水压力值之间的差值是否不超过5%。同时满足上述两个条件，则地下水渗流方程的数值解正确。

表1 填砾抽灌同井参数取值Table 1 Parameter selection of FECSCW

图5为地下水渗流方程的数值解。当渗透系数各向同性时，krr=kzz，ρ=1，Z=z；当渗透系数各向异性时，krr/kzz=0.5，krr/kzz=2。由式（17），（18）得到地下水压力和地下水流动速度。地下水渗流方程的解析解如图6所示。

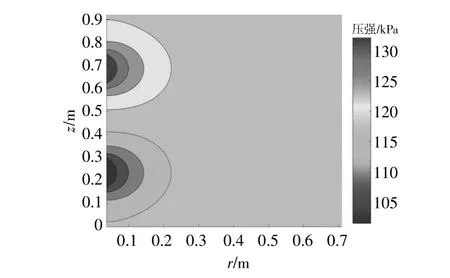
图5 地下水渗流方程的数值解Fig.5 Numerical solution of groundwater seepage equation

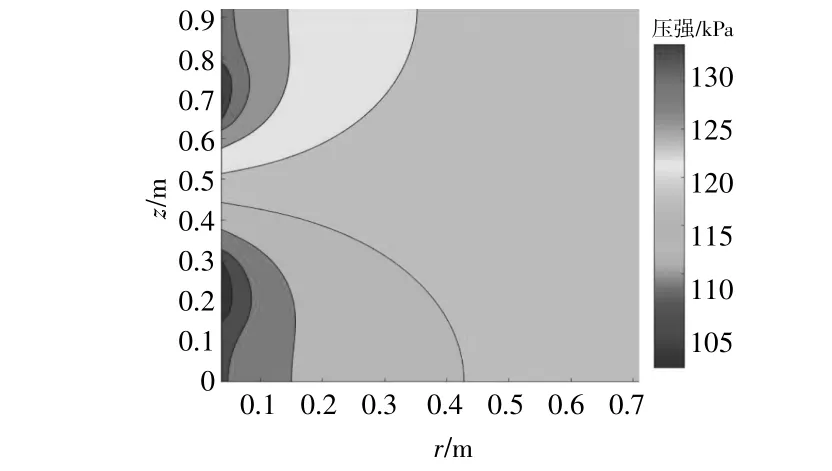
图6 地下水渗流方程的解析解Fig.6 Analytic solution of groundwater seepage equation

由图5，6可知，地下水压力分布关于z=0.48反对称，抽水区的地下水压力小于含水层的初始地下水压力时，含水层中的原水进入抽水滤网；回水区的地下水压力大于含水层的初始地下水压力时，回水回灌到含水层。由图5，6还可以看出，含水层上、下顶板的地下水压力沿含水层竖直方向没有变化，与含水层上、下顶板的边界条件相对应。在图5中选取3个不同点的地下水压力值，这3个 点的 坐 标 分 别 为H（0.4 ，0.6 ），H（0.1 ，0.7 ），H（0.5 ，0.8 ），相应的地下水压力值分别为118.88 ，129.72 ，118.71 kPa；在图6中选取3个不同点的地下水压力值，这3个点坐标分别为H（0.4 ，0.6 ），H（0.1 ，0.7 ），H（0.5 ，0.8 ），相应的地下水压力值分别为119.68 ，127.72 ，114.21 kPa。

3组误差的平均值为2.0%，因此，利用地下水渗流方程的解析解可以验证数值解，并且地下水渗流方程的数值解满足上文的2个条件，因此，地下水渗流方程的数值解正确。地下水渗流方程的解析解与数值解之间的偏差由数学化简所致，数学简化可分为两步，第一步为假设地下水渗流方程中2个自变量互不影响，地下水渗流方程由偏微分方程化简为微分方程；第二步为采用有限差分法将微分方程化简为差分方程。提高数值解精度的方法为通过加密网格，使差分方程无限逼近微分方程。

含水层的地下水速度矢量图如图7所示。

图7 含水层的地下水速度矢量图Fig.7 Groundwater velocity vector of aquifer

由于图6中抽水区与回水区之间存在地下水压力差，迫使图7中含水层的原水和回灌水从回水区流动到抽水区，从而发生流贯通，因此，填砾抽灌同井回水滤网与抽水滤网之间应设置挡板。回水区z=0.70 处水流的速度方向为向右，z=0.45处水流的速度方向为向下，水流速度方向的改变，消耗了大量动能，导致z=0.45 处水流的速度很小。由图7可知，抽、回水区水流的速度随含水层半径的增大而减小。

图8为在同一深度下不同点处含水层的渗透系数之比对地下水压力的影响

图8 在同一深度下不同点处含水层的渗透系数之比对地下水压力的影响Fig.8 The influence of the ratio of permeability coefficients of aquifers at different points at the same depth on groundwater pressure

由图8可知：在z=0.69 处，地下水压力随着不同点处含水层渗透系数之比的增大而增大，在z=0.23 处，地下水压力随着不同点处含水层渗透系数之比的增大而减小；抽水区与回水区之间的地下水压力差随着不同点处含水层渗透系数之比的增大而增大。通过分析发现：地下水压力随着不同点处含水层渗透系数之比的增大而增大；含水层中地下水流动方向与抽、回水口水流方向不一致会导致地下水消耗大量动能；地下水动能来源于抽、回水水泵的扬程；对于渗透系数之比大于1的含水层应选用扬程大的水泵。

图9为在同一半径下不同点处含水层的渗透系数之比对地下水压力的影响。

由图9可知，当krr/kzz=2时，r=0.07 ～0.23 m处，地下水压力变化幅度剧烈；当krr/kzz=0.5 时，r=0.07 ～0.23 m处，地下水压力变化幅度平缓，抽、回水的影响范围随着含水层渗透系数之比的减小而减小。此外，图9中地下水压力曲线相交于一点，该点坐标为z=0.48 m，这与抽、回水区地下水压力分布关于z=0.48 m反对称相对应。

4 结论

本文统一3种热源井壁面处的渗透系数，建立填砾抽灌同井地下水渗流方程，使用分离变数法、傅里叶变换和有限差分法，分别得到地下水渗流方程的解析解和数值解，并对地下水渗流方程的解析解和数值解进行对比得到如下结论。

①通过表皮效应建立循环单井、抽灌同井和填砾抽灌同井壁面处渗透系数的转换关系式。

②以填砾抽灌同井为例，本文建立稳态承压含水层地下水渗流方程及边界条件，获得填砾抽灌同井的降深方程。通过渗透系数转换关系式，本文得到抽灌同井和循环单井的降深方程。本文利用有限差分法对地下水渗流方程进行离散，并编写计算程序，求得填砾抽灌同井的地下水渗流方程数值解。计算结果表明，地下水渗流方程的数值解和解析解的平均误差为2.0%，误差来源于数学化简，减少误差的方法为加密网格，加密网格使得地下水渗流方程的数值解无限逼近解析解，填砾抽灌同井的地下水渗流方程可用于解决该热源井影响下的稳态无越流承压含水层的地下水流动问题。

③抽、回水区的压力分布关于z=0.48 m反对称。填砾抽灌同井出现流贯通现象。抽、回水的影响范围随着不同点处含水层渗透系数之比的增大而增大。渗透系数之比大于1的含水层应选择扬程大的水泵；在填砾抽灌同井回水滤网与抽水滤网之间的含水层设置挡板后，能够有效减缓流贯通的趋势。