南北向真空管太阳能集热器日采光量的简化计算方法研究

吴茂刚，张有刚，唐润生

（云南师范大学 太阳能研究所，云南 昆明650500）

0 引言

全玻璃真空管太阳能集热器因其保温性能好，且易于规模化生产、运输和安装，在我国得到了广泛应用，其使用量约占市场份额的95%[1]～[4]。在实际应用中，真空管太阳能集热器排列方式分为水平排列和垂直排列，前者主要用于集中供热的太阳能热水系统，后者主要用于家用太阳能热水器。家用真空管太阳能热水器通常采用南北方向倾斜排列，其热性能通常依据集热器平面接收到的太阳辐照量进行评定。现有检测方法得到的结果不能真实反映真空管太阳能集热器的热性能，这是由于以下几点：①真空管太阳能集热器的实际采光量不同于真空管太阳能集热器平面接收到的太阳辐照量；②真空管太阳能集热器的实际采光量无法通过测量直接得到；③真空管太阳能集热器的实际采光量与真空管取向、真空管间距和安装倾角有关[5]，[6]。

2004年，Shah提出了垂直排列的真空管太阳能集热器采光量理论计算方法[7]。2009年，Tang依据太阳几何学及辐射传输理论，建立了更加详细的真空管太阳能集热器采光量计算方法，并以此为基础分析了真空管太阳能集热器年采光量最大时的最佳安装倾角[5]。由于真空管的采光量取决于太阳光线在真空管横截面上的投影角和拦截面上的入射角，并且这两个变量均随着时间不断发生变化，因此，无论采用哪种理论计算方法，真空管太阳能集热器日采光量的计算都必须借助数值计算技术。真空管散射日采光量的计算往往采用二维天空辐射模型，即假设天空辐射在真空管横截面上的方向强度为各向同性。但Li的最新研究结果显示，倾斜安装的真空管横截面上的天空辐射强度并非各向同性[8]，这意味着采用二维天空辐射模型计算倾斜排列的真空管太阳能集热器散射辐射采光量存在一定的计算误差。

长期以来，测量和评定真空管太阳能集热器的热性能均依据集热器平面接收到的太阳辐照量，这是由于真空管太阳能集热器的实际采光量无法通过直接测量得到，而理论计算的方法又十分复杂[9]，[10]。理论上，真空管间距越大，真空管相互遮挡的面积越少，集热器的热性能越好，但依据现有的检测方法可知，真空管间距越大，集热器单位面积接收到的太阳辐照量越小，其热性能越差[11]。此外，在太阳能热利用工程设计过程中，须要准确计算真空管太阳能集热器的实际采光量。本文在前期研究的基础上，建立了南北向真空管太阳能集热器（Northsouth oriented Evacuated Tube Collector，NSETC）日采光量的简化计算方法，为家用真空管太阳能热水器的性能检测、评定提供了方法和理论基础。

1 南北向真空管太阳能集热器采光量的计算方法

1.1 NSETC日直射辐照量的通用计算方法

假设NSETC与水平面的夹角为β，南偏西放置，方位角为φ，无漫反射板。为了便于分析，本文建立了确定太阳位置的坐标系，如图1所示。图中X轴垂直于真空管太阳能集热器平面；Z轴平行于真空管，并指向北方；Y轴平行于地面，并指向东方（朝向为东偏南，方位角为φ）。坐标系X0Y0Z0为地平坐标系，X0轴指向天空，Z0轴指向正北，Y0轴指向东方。

图1 确定太阳位置的坐标系Fig.1 The coordinate system used to determine the position of the sun

太阳光线在真空管横截面的投影如图2所示。

图2 太阳光线在真空管横截面的投影Fig.2 The projection of light rays on the cross section of a solar tube

图中θp为太阳光线在真空管横截面上的投影与真空管平面法线之间的夹角（以下简称为投影入射角）。

各真空管在任意时刻所接收的太阳直射辐照度Ib，t的计算式为

式中：D1为真空管内管的直径；Ib为法向太阳直射辐照度；θt为太阳光线在真空管拦截面上的入射角；f（θp）为真空管对太阳辐射的拦截系数。

f（θp）的计算式为[6]

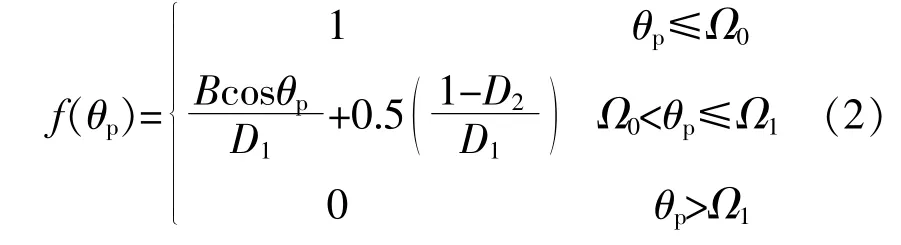
式中：D2为真空管外管的直径；B为相邻真空管的中心距；Ω0，Ω1分别为相邻真空管出现遮挡时和完全遮挡时，太阳光线在真空管横截面上的投影与真空管平面法线之间的夹角。

真空管拦截面的法线与入射光在真空管横截面上的投影重合（图2），因此，光线在真空管拦截平面上的入射角θt的计算式为

式中：ns为入射光线向量，ns=（nx，ny，nz）；ns，XOY为入射光在真空管横截面上的投影向量。

其中，ns，XOY的计算式为

θp的计算式为

其中，nx，ny的计算式分别为[5]

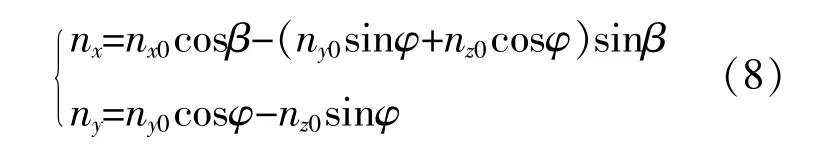
式中：nx0，ny0，nz0为入射光线向量ns在地面坐标系的坐标分量。

nx0，ny0，nz0的计算式分别为[12]

式中：λ为当地地理纬度；ω为太阳时角；δ为太阳的赤纬角。

δ的计算式为

式中：n为1月1日与测试日之间的天数。

假设真空管太阳能集热器由N支真空管组成。真空管能够被太阳光线照射到的长度为L。在不考虑真空管太阳能集热器边缘效应的情况下，真空管太阳能集热器单位面积的日直接辐射采光量Hb，t的计算式为

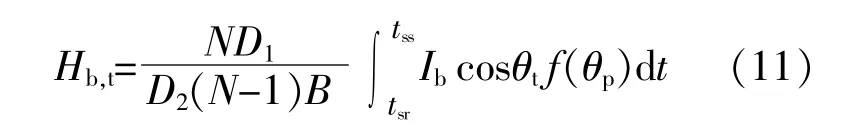
式中：tsr，tss分别为太阳在真空管太阳能集热器平面上的日出和日没时间。

真空管太阳能集热器单位平面上的日直射辐照量Hb，s的计算式为

在实际应用中，通常只能采集到水平面上的太阳辐照量，此时Hb，t的计算式为

式中：Hh为水平面上的日总辐照量；Hb，s为集热器平面接收到的日直射辐照量；Hd为水平面上的月平均日散射辐照量；Hb，t为真空管太阳能集热器单位面积接收到的日直接辐射采光量；Rb，t-s为Hb，t与Hb，s的比值；Rb，s-h为Hb，s与水平面上的日直射辐照量的比值；Rb为单位集热器面积上接收到的日直射辐照量与水平面上接收到的日直射辐照量的比值。

Rb，t-s，Rb，s-h的计算式分别为

式中：t0为地面上的日落时间。

t0的计算式为

式中：ω0为日落时角。

ω0的计算式为

Rb的计算式为

一天的时间长度τday=24 h。如果已知一天内法向太阳直射辐照度随时间的变化规律，则可以通过数值计算直接求出Rb，t-s。Tang通过研究发现，当真空管太阳能集热器安装倾角偏离纬度不大于10°（即|β-λ|≤10°）、方位偏离正南方不大于20°（|φ|≤20°）时，Rb，t-s随倾角β和方位角φ的变化非常小[10]。换言之，在这种情况下，Rb，t-s可按照β=λ，φ=0进行计算。因此，本文基于β=λ，φ=0计算Rb，t-s，根据简化计算方法，基于实际的倾角和方位角计算Rb，s-h。Ib为时间的函数，当β=λ，φ=0时，可以直接推导出Rb，t-s和Rb，s-h的计算式，从而避免采用数值计算方法。

1.2 NSETC日直射辐照量的简化计算方法

当倾角β=λ，方位角φ=0时，cosθt=cosδ，θp=|ω|，此时式（14）可简化为

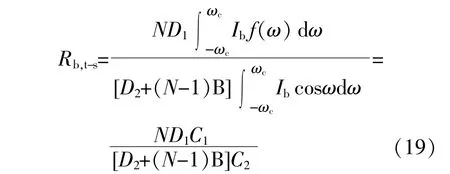
式中：C1，C2均为系数；ωc为太阳在真空管太阳能集热器平面上的日没时角。

其中，ωc的表达式为

如果已知Ib为关于时间t或者太阳时角ω的函数，可以直接根据式（19）推导出Rb，t-s的计算式。在进行与太阳辐射相关的计算过程中，学者们广泛采用当地气象部门提供的多年水平面月总日辐照量或月平均日辐照量（Hh）数据。已知Hh，可利用Collares-Pereira提出的经验公式求得Hd，具体的计算式为[12]

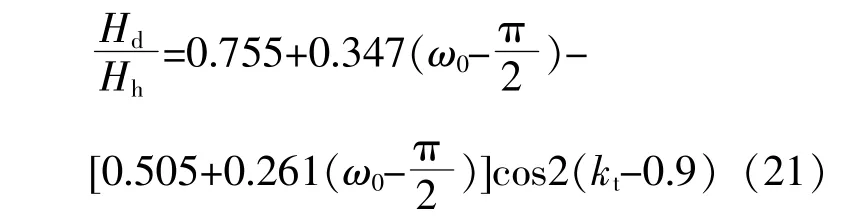
式中：kt为月平均大气透明指数。

kt的计算式为

式中：H0为大气层外水平面上的月平均日辐照量。

H0可以基于各月代表日的δ得到，δ的表达式为

式中：I0为太阳常数，I0=1 373W/m2。

水平面上任意时刻太阳辐照度的相关计算式分别为

式中：a，b为计算系数；Id为水平面散射辐照度；Ih为水平面总辐射辐照度；rd为水平面散射辐照度Id与水平面日总散射Hd的关系式。

a，b的计算式分别为

将式（24）代入式（19）整理得到下面计算

式中：a＇为计算系数；Ωx为临界角。

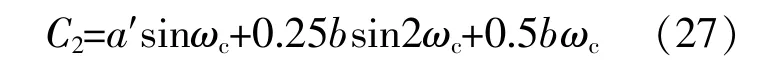
Ωx的计算式为

a＇的计算式为

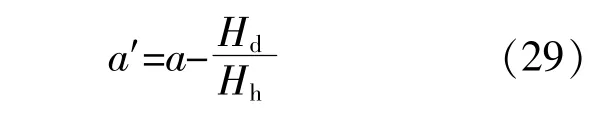
如果Ωx≤Ω0，则C1的计算式为

同样，将式（24）代入方程（15）得到如下关系式。

式中：ωsr，ωss分别为太阳在真空管太阳能集热器平面上的日出、日没时角；A2，B2，C3，D3均为计算系数。

ωsr，ωss可由nx=0，结合水平面日出、日没时间来确定。

当方位角φ=0时，ωsr，ωss和ωs的计算式分别为

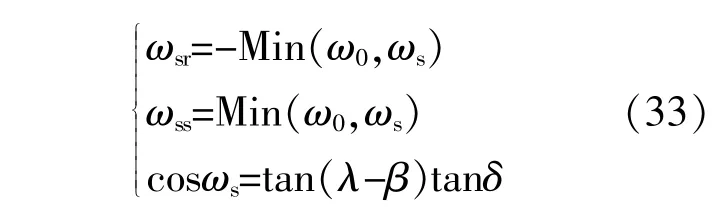
当方位角φ＞0时（南偏西），ωsr，ωss的计算式分别为

式中：ω1，ω2为非正南放置的集热器表面的“视日落”和“视日出”时角。

当方位角φ＜0时（南偏东），ωsr，ωss的计算式分别为

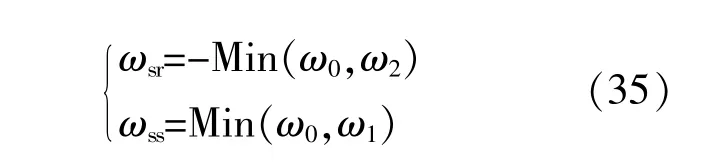
ω1，ω2的计算式分别为

E1，E2的计算式分别为

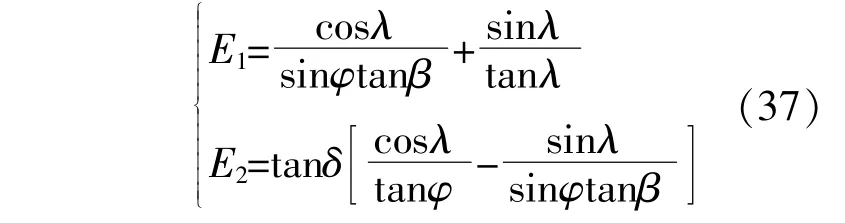
1.3 NSETC所接收的散射辐照量计算

1.3.1 二维天空辐射模型

假设散射辐射在倾斜安装的真空管横截面上的方向辐射强度为各向同性，此时与横截面之间角度为dθp的天空辐射与拦截面之间的夹角θt为0°。在此条件下，单支真空管在任意时刻接收到的散射辐照度为

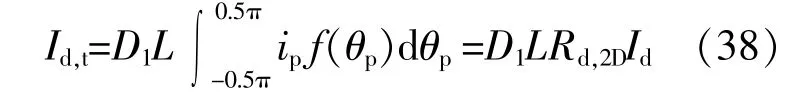
式中：ip为真空管横截面上天空辐射的方向辐射强度；Rd，2D为基于二维天空辐射模型的NSTEC对天空辐射的采光系数。

本文中来自各方向的天空辐射的累计值为真空管平面上所接收到的散射辐照度，其计算式为

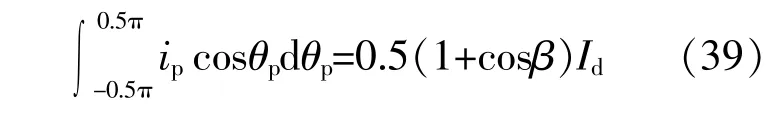
由此得到ip的计算式为

将式（2）代入式（38）得到Rd，2D的计算式为

单位集热器面积所接收到的日散射辐照量Hd，t的计算式为

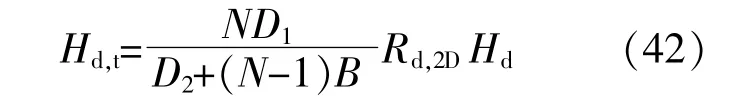
图3为计算天空辐射所用的球坐标。

图3 计算天空辐射所用的球坐标Fig.3 Spherical coordinates used to calculate sky radiation

1.3.2 三维天空辐射模型

Li通过研究发现，对于各向同性的天空辐射，倾斜安装的真空管横截面上的方向辐射强度ip不是常数，与θp有关[8]。因此，真空管所接收到的天空辐射应根据三维天空辐射模型对真空管太阳能集热器平面上方的天空进行积分计算，具体的计算式为

式中：i为天空辐射的方向强度；θin，h为来自微元的辐射光线与水平面之间的夹角；g（θin，h）为控制函数；Rd，3D为基于三维天空辐射模型的NSTEC对天空辐射的采光系数。

令地面所接收到的天空辐射的累计值为Id，其计算式为

由式（44）得到i=Id/π。在图3所示的坐标中，来自天空任意微元（d=sinθdθdφ）的天空辐射的单位向量ns、投影入射角θp和拦截面上的入射角θt的计算式分别为

在图3所示的坐标系中，水平面的法线的单位向量为nh=（cosβ，0，sinβ），因此，可得：

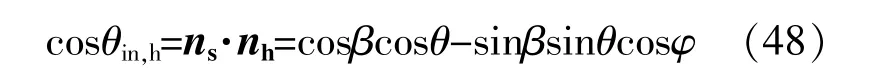
当cosθin，h＞0时，g（θin，h）=1，否则为0。这是由于太阳光线所来自的天空微元位于地面之下，不属于真空管太阳能集热器“所看到”的天空范围。利用上述关系式对真空管太阳能集热器上方的半球空间（0≤θ≤0.5 π，0≤φ≤2π）进行积分，可得到Rd，3D的计算式为

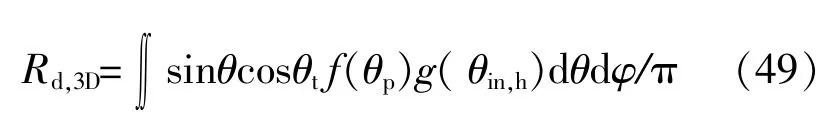
2 估算值与直接数值计算结果的对比

2.1 基于二维和三维模型计算的采光系数对比

图4为基于二维和三维天空辐射模型NSTEC得到的天空辐射采光系数Rd，2D与Rd，3D，以及Rd，2D与Rd，3D的比值随集热器安装倾角β的变化情况。

图4 R d，2D与R d，3D及其比值随集热器倾角的变化Fig.4 Variationsof R d，2D，R d，3D and R d，2D/R d，3D with collector's tilt-angle

由图4可知，Rd，2D/Rd，3D的值与集热器安装倾角β和真空管间距B有关。B越大，Rd，2D与Rd，3D的比值越大，即Rd，2D与Rd，3D之间的偏差越大；当B=80mm时，二者的最大偏差为0.65%，此时，β为59°；而当β=0°，90°时，Rd，2D与Rd，3D相等，这一结果与Li的研究结果相一致[8]。综上可知，对于倾斜安装的真空管，其横截面上接收到的天空辐射强度不是各向同性的，因此，真空管接收的天空辐射须要按照三维天空辐射模型进行计算，但依据二维和三维天空辐射模型计算得到的采光系数差异不大，在实际应用中可以用二维辐射模型来简化真空管天空辐射采光量的计算过程。

由图4还可看出，当真空管太阳能集热器的安装倾角小于38°时，采光系数Rd＞1，表明真空管所接收的天空辐射大于水平面所接收的天空辐射，因此，适当降低真空管太阳能集热器的安装倾角有利于天空辐射的接收，特别是在太阳能资源较差的地区。

2.2 日直射辐照量的估算值和数值计算结果对比

为了评价本文所建立的简化计算方法的可靠性，本文以2020年4月16日（n=106，δ=9.44 °）昆明地区的太阳辐照度实测数据（Hh=23.46 MJ/m2，Hd=8.57 MJ/m2）为基础，对采用简化方法[式（19）～（30）]所得到的Rb，t-s，Rb与采用直接数值计算方法[式（14），（15）]得到的结果进行对比分析。在日直接辐射采光量的数值计算过程中，所采用的时间歩长为1min，各时刻的太阳辐照度可根据每5min的实测值结合线性内插法来确定。

图5为根据经验公式得到的太阳辐照度计算值以及太阳辐照度实测值随时间的变化情况。

图5 太阳辐照度计算值与太阳辐照度实测值随时间的变化Fig.5 The calculated and measured solar irradiance varieswith time

由图5可知，水平面总太阳辐照度的实测值Ih与根据经验公式计算得到的计算值基本一致，标准平方偏差NMBE为-1.8%，但法向太阳直接辐照度Ib的实测值与根据经验公式计算得到的计算值相差较大，并且在早晨二者的差距最大。

依据太阳辐照度实测值，分别采用简化计算方法（估算）和数值计算方法得到Rb，t-s。图6为对于昆明地区管间距B为80mm且面向正南方向安装的真空管太阳能集热器，其Rb，t-s的估算值Rb1，t-s和计算值Rb2，t-s以及二者的比值随β-λ的变化情况。

图6 R b，t-s的估算值和计算值随β-λ的变化情况Fig.6 Comparisons of R b，t-s between estimated and direct numerically calculated

由图6可知，当（β-λ）＞15°时，Rb1，t-s高于Rb2，t-s，但两者的差值很小。当集热器安装倾角偏离纬度值不大于10°时（|β-λ|≤10°），Rb1，t-s与Rb2，t-s之间的相对偏差小于0.4%。

图7为对于昆明地区管间距B为80mm，且非正南方向安装的真空管太阳能集热器，不同安装倾角条件下，Rb1，t-s/Rb2，t-s随φ的变化情况。

图7 R b，t-s的估算值和计算值随方位角的变化情况Fig.7 Comparisons of R b，t-s between estimated and direct numerically calculated

当集热器方位角偏离正南不大于20°（φ≤20°）时，Rb1，t-s与Rb2，t-s之间的相对偏差小于2%。

图8为Rb，t-s的估算值和计算值随集热管间距的变化情况。

图8 R b，t-s的估算值和计算值随集热管间距的变化情况Fig.8 Comparison of R b，t-s between estimated and direct numerically calculated for different tube spacing

由图8可知，当集热管间距B为70～80mm时，Rb1，t-s和Rb2，t-s之间的相对偏差小于0.2%。由图8还可看出，随着集热管间距逐渐增大，Rb1，t-s，Rb2，t-s均呈现出线性下降的变化趋势，表明随着集热管间距逐渐增加，集热器单位面积所接收到的太阳直接辐射采光量逐渐下降。若依据现行的热水器性能评定方法，集热器的性能会随着集热管间距的增加而下降；但实际情况恰恰相反，随着集热管间距逐渐增加，集热管之间相互遮挡情况逐渐减少，集热器的采光量会相应增加，导致其集热性能随之提升[5]。这表明即使集热管的集热性能完全相同，不同管间距条件下真空管太阳能集热器的集热性能不具备可比性。

图9为面向正南方向安装的真空管太阳能集热器，当加热管间距B为80mm时，Rb的估计值Rb，est和计算值Rb，cal以及二者的比值随β-λ的变化情况。

图9 R b的估计值和计算值随β-λ的变化情况Fig.9 Comparison of R b estimated and numerically calcuated

由图9可知，对于面向正南方向安装的真空管太阳能集热器，当集热器安装倾角偏离地理纬度不大于10°时，Rb，est与Rb，cal之间的相对偏差小于0.5%。

图10为对于非正南方向安装的真空管太阳能集热器，当集热管间距B为80mm时，不同安装倾角条件下，Rb，est/Rb，cal随φ的变化情况。

图10 R b的估计值和计算值随方位角的变化情况Fig.10 Comparison of R b estimated and numerically calcuated

由图10可知，对于非正南方向安装的真空管太阳能集热器，当集热器方位角偏离正南方向小于20°时，两者的相对偏差小于2.2%。上述分析结果表明，在实际应用中可依据水平面所测得的日直射辐照量（Hh-Hd）或真空管太阳能集热器平面上的日直射辐照量（Hb，s），以及本文所提出的简化计算方法得到的Rb或Rb，t-s来估算真空管太阳能集热器的日直接辐射采光量。估算值与计算值出现差异的原因有两个：一是实际的辐照度随时间的变化规律与Collares-Pereira提出的经验公式存在差异（如图5所示）；二是本文所提出的简化计算方法是适用于朝向为正南方向、安装倾角为地理纬度的真空管太阳能集热器，而精确的数值计算依据实际的安装倾角和方位角。

2.3 年采光量的估算值与数值计算结果对比

为了验证利用本文提出的简化计算方法计算真空管太阳能集热器年采光量的可靠性，本文基于我国10个典型城市多年水平面月总太阳辐照量，利用两种计算方法分别计算了每天的直接辐射采光量和天空辐射采光量，最终得到真空管太阳能集热器的年直接辐照量Sb和总辐照量Sa，并对估算结果和数值计算结果进行对比。

图11为对于正南方向安装的真空管太阳能集热器，当加热管间距B为80mm时，不同地区Rb，est/Rb，cal随β-λ的变化情况。

图11 不同地区R b，est/R b，cal随β-λ的变化情况Fig.11 Comparison of annual collectible radiation between estimated and numerically calculated

由图11可知，对于朝向为正南方向的真空管太阳能集热器，当安装倾角偏离地理纬度小于10°时，年直射辐照量的估计值与计算值之间的相对偏差小于0.2%。

图12为对于北京地区非正南方向安装的真空管太阳能集热器，在不同β条件下，Rb，est/Rb，cal随φ的变化情况。

图12 R b，est/R b，cal随方位角φ的变化情况Fig.12 Comparison of annual collectible radiation between estimated and numerically calculated

由图12可知，对于非正南方向安装的真空管太阳能集热器，随着集热器安装倾角β和方位角|φ|逐渐增加（由于Collares-Pereira提出的经验关系所计算出来的年采光量关于φ=0°面对称，因此，图12只给出了φ＞0°时的计算结果），Rb，est与Rb，cal之间的偏差逐渐增加，当|φ|＜20°且β＜λ+10°时，Rb，est与Rb，cal之间的相对偏差小于1%。

表1为当β=λ+10°，φ=20°时，利用简化计算方法和数值计算方法得到的我国10个主要城市年直射辐照量和总辐照量。表中：Sa，est为根据简化计算方法和二维天空辐射模型参数Rd，2D计算得到的年总辐照量（MJ/m2）；Sa，cal为根据数值计算方法和三维散射辐射模型参数Rd，3D计算得到的年总辐照量。

表1 当β=λ+10°，φ=20°时，我国10个主要城市年直射辐照量和总辐照量的估算值和计算值Table 1 Comparison of estimated and numerically calculated annual beam and global irradiation for 10 cities

城市 纬度 Sb，estSb，calSb，est/Sb，calcSa，estSa，calSa，est/Sa，calc

由表1可知，除了拉萨、昆明外，随着纬度逐渐增加，Sa，est与Sa，cal，Sb，est与Sb，cal的相对偏差均逐渐增加，但均小于1%。

3 结论

本文在集热器安装倾角β偏离地理纬度λ不大于10°、方位角φ偏离正南方向20°的条件下，分析了Rb，t-s随β和φ的变化情况，并基于Collares-Pereira提出的太阳辐射计算经验公式，提出了计算南北向安装的真空管太阳能集热器日采光量的简化计算方法。

①在|β-λ|≤10°，|φ|≤20°的情况下，Rb，t-s的估算值与数值计算结果之间的相对偏差小于2%。

②Rb的估算值与数值计算结果之间的相对偏差小于2.2%，因此，在实际应用中，当真空管太阳能集热器的安装倾角偏离地理纬度不大于10°、方位角不大于20°时，真空管太阳能集热器的日直接辐射采光量可分别依据估算得到的Rb，t-s和Rb，并结合真空管太阳能集热器平面和水平面所测得的日太阳直接辐射量来估算。

③基于二维和三维天空辐射模型计算的真空管太阳能集热器，对天空辐射的采光系数均与集热器安装倾角有关，当安装倾角小于60°，二者的相对偏差小于0.65%。

④在|β-λ|≤10°，|φ|≤20°的情况下，基于简化的太阳直接辐射和二维天空辐射模型计算得到的真空管集热器年总采光量，与基于数值计算方法和三维天空辐射模型得到的年总采光量之间的相对偏差小于1%。