双馈风电机组HVRT暂态电流计算及其控制策略研究

兰传盛，潘庭龙

（江南大学 物联网技术应用教育部工程研究中心，江苏 无锡214122）

0 引言

近十几年风力发电获得迅猛增长，双馈风力发电机组（DFIG）是目前风力发电系统的首选[1]。电网电压骤升故障会在DFIG定子绕组中产生暂态直流分量[2]，[3]，引起比电网电压跌落更强的双馈发电机定、转子电流的冲击，严重影响机组的稳定运行。因此，研究DFIG的高电压穿越（HVRT）性能显得尤为必要。

电网电压骤升成因一般为低压故障恢复后无功过补偿、负载突降和单相接地故障等[4]。为保证电网运行的安全与稳定性，避免风电机组因电压保护作用而从电网中解列，风电场须具备HVRT能力[5]。转子电流是衡量机组HVRT的重要指标，转子电流取决于电机的控制策略和电磁方程[6]，其暂态特性较为复杂，因此DFIG故障下的电流分析和计算也是当前一个重点[7]，[8]。

与低电压穿越（LVRT）下短路电流相似的是，在电压骤升引起的定、转子电流冲击并入电网后，会对电力系统的距离保护、测试和故障分析等产生影响[9]，且一些HVRT控制策略的制定都须获得转子电流精确表达式[10]～[13]。文献[14]分析了短路电流受LVRT控制策略影响后的变化过程，但未深入分析无功控制下转子电流的变化情况。文献[15]，[16]考虑撬棒投入、网侧变流器及无功控制对转子电流的影响，但未考虑控制切换带来的启动延时问题。文献[17]分析了电网电压骤升及恢复过程中双馈电机电磁过渡过程，但忽略了HVRT过程中crowbar电路一般不投入使用，且未具体分析转子电流波动情况。文献[18]分析了故障发生和切除时转子电流的变化，但忽略了控制启动延时和无功输出带来的影响。

鉴于此，本文研究了电压骤升故障下DFIG转子电流的暂态特性，并考虑无功控制和启动延时带来的电流暂态特性变化，给出了不同状态下电流变化公式，得出故障后转子电流变化模型。利用优化后转子电流表达式，设计了一种对称骤升故障下转子过电流抑制方式，达到高电压穿越的目的。最后，仿真验证了该转子电流计算方法和转子电流抑制策略的正确性。

1 电网电压骤升故障下DFIG特性

本文建立了DFIG数学模型，不考虑磁饱和，电机的定、转子侧采用电动机惯例，归算至定子侧。

两相静止坐标系下DFIG数学模型[19]为

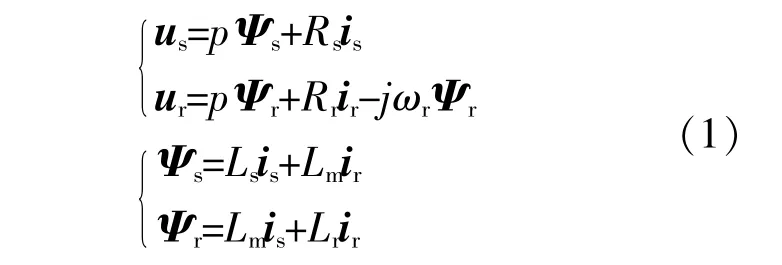
式中：u，i和Ψ分别为电压矢量、电流矢量和磁链矢量；p为微分算子；下标s，r分别为定子和转子分量；R和L分别为电阻和电感；ωr为转子角速度；Lm为定转子间互感。

在t=0时刻，电网发生对称骤升故障，忽略定子电阻的影响，突变前后定子磁链暂态表达式[20]为

式中：Us为电网电压幅值；h为骤升比率；ω1为同步旋转角速度；τs为定子时间常数，τs=Ls/Rs，Rs和Ls分别为定子电阻和定子电感。

根据当前国际并网准则，在h＞0.3 之后，机组可脱网运行[21]，因此本文考虑的h为0～0.3 。故障后定子磁链的自由分量和强制分量决定转子开路电压的两个分量的取值[22]，转子开路电压为

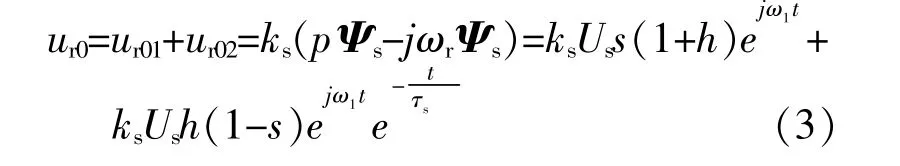
式中：ur01，ur02分别为强制分量和直流分量；ks=Lm/Ls；s为滑差，s=（ω1-ωr）/ω1。

若求转子电流交流分量，可将转子开路电压的两个分量与转子变换器作用于转子侧的电压ur03视为3个独立电源，共同作用后变换到转子侧，其等效电路如图1所示。

基于上述风电机组模型，根据叠加原理，将转子电流交流分量分解为3个电压源同时作用。由于转子开路电压的直流分量表现为以转子速度旋转及转子时间常数τr（τr=σLr/Rr）幅值衰减，因此须转换至转子坐标系，可得转子电流交流分量为

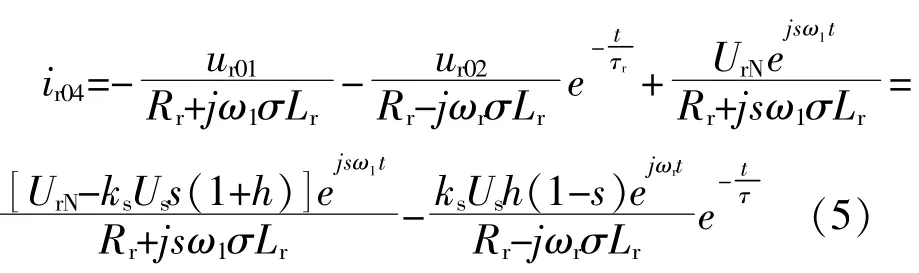
其中τ=τsτr/（τs+τr），由于转子电流流过电感，电流不突变，转子电流在故障时刻前后幅值为

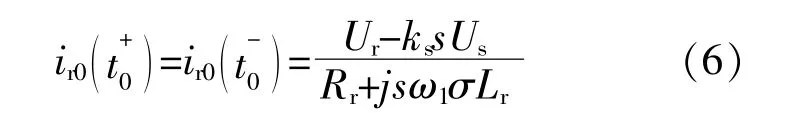
由转子电流的直流分量的衰减τr=σLr/Rr，得到直流分量表达式：

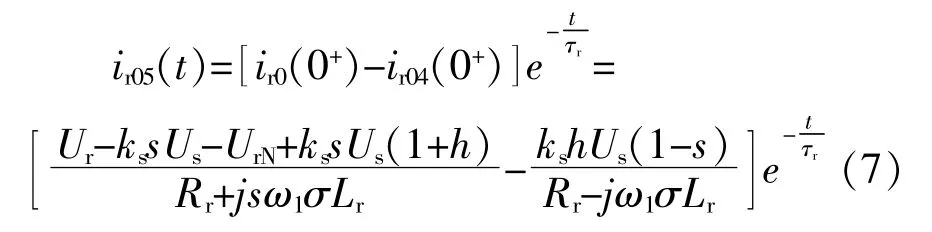
2 HVRT控制下转子电流计算

电网电压骤升故障下，要求DFIG持续工作不脱网，定子电压的突变会引起转子感应电势变化，接着转子侧控制器根据骤升幅度调整控制策略，设置不同的转子电流指令值，实现电压穿越，此时转子电流指令值的变化影响了转子电流的暂态特性。电网电压骤升故障瞬时发生，而转子电流指令值的调整存在延时，须根据骤升幅度改变转子电流指令值。且电网发生骤升故障时，机组为电网提供无功支持，因而转子电流指令值的设置受无功控制影响。

故障后电流变化可分为两个步骤：①在故障发生后Δt时刻内，电网电压骤升，转子感应电势发生变化，导致转子电流迅速变化；②在故障发生Δt时刻之后，转子侧变换器根据故障程度和无功需求调整转子电流指令值，转子电流指令值改变，转子电流随之变化。

针对启动延时和无功控制的影响，本文主要考虑切换状态下边界条件的变化。在t=0 s～无功控制策略投入时不受控制策略切换的影响，转子电流故障边界条件改变时，转子电流值为

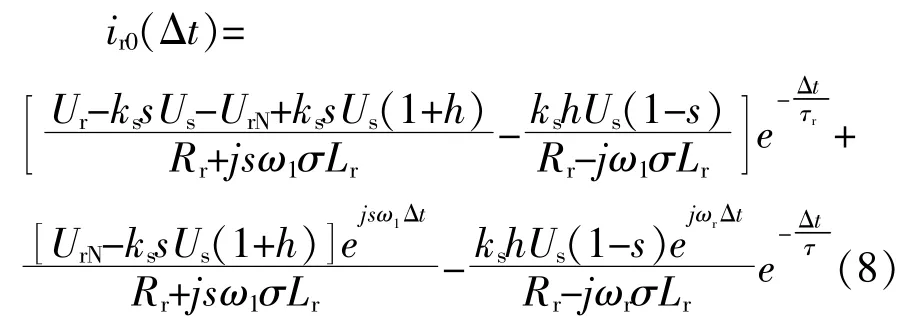
采用文献[23]方法设置有功、无功电流，优先向电网输出一定的感性无功功率，为故障电网提供无功支持。根据电压骤升幅度确定转子电流指令值，有：

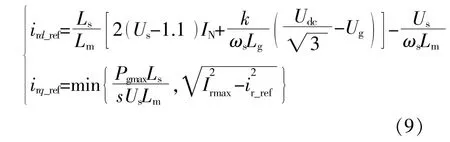
式中：ird_ref，irq_ref分别为d-q轴上转子电流指令值；ir_ref为转子电流指令值；Ug为网测电压额定值；IN为机组额定定子电流；Udc为额定直流侧电压；Pgmax为网测最大输出有功功率；k为防过调制系数。

转子侧变流器采用电流内环控制，表达式[24]为式中：kp，ki分别为PI控制器的比例系数和积分系数。

取切换延时后转子电流ir0（Δt）作为起始值，联立式（1），（2）和（10），可得转子电流微分方程为

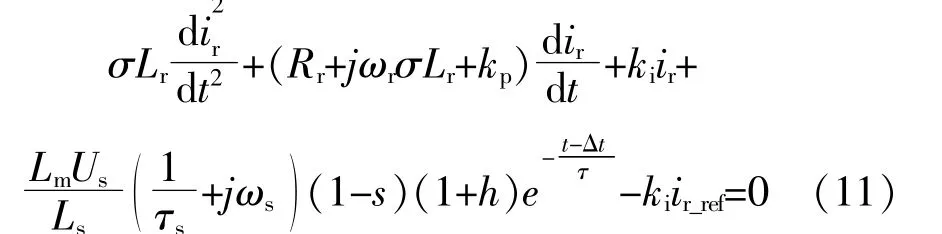
求解该转子电流微分方程，可得方程通解和特解，得到转子电流指令值调整后的转子电流表达式：

3 限流控制策略

本文讨论了无功需求下转子电流指令值的设定以及该转子电流指令值对转子电流的影响，提供了一种求解电压骤升故障下转子电流的思路。切换后的控制策略设置不同，转子电流的暂态特性也随之变化。

由式（5）和式（7）可知骤升故障后和转子电流指令值设定前转子电流的暂态变化，对A相电流进行分析，有表达式：

通过以上分析，为使转子电流在d-q轴上的分量在正常范围内，L值设置为

考虑式（5）和式（7）转子电流变化，综合L值计算过程，本文提出了一种限制转子电流的HVRT控制的计算方法，DFIG转子侧的控制结构如图2所示。转子侧变流器采用定子电压定向矢量，功率外环、转子电流闭环的控制方法，最大风能跟踪和无功功率控制在DFIG转子侧进行。在传统的转子电流闭环控制的基础上，增加转子电流抑制（RCR）控制器，RCR控制器可在故障时加强对转子电流的控制，其设置由式（14）和式（15）确立。当电网正常运行或电网电压Vs＜1.1 p.u.时，通过信号比较器，切换至正常运行状态，给定L=1；当电网故障发生时，信号比较器检测到电网电压Vs＞1.1 p.u.，此时加入RCR控制器，给定L值，然后通过限制器将L值限制在一定范围内，可将转子电流在d-q轴的分量控制在正常范围内，有效避免了转子过流对变流器的影响。

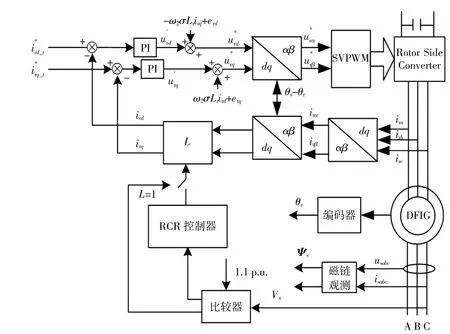
图2 DFIG控制策略流程图Fig.2 Flow chartof control strategy for doubly-fed induction generator

4 仿真分析

为证明本文转子电流计算的精确性与所设计高电压控制策略的有效性，采用文献[23]所提控制策略，在Matlab/Simulink环境下搭建了1.5 MW的DFIG仿真模型，DFIG的主要参数如表1所示。

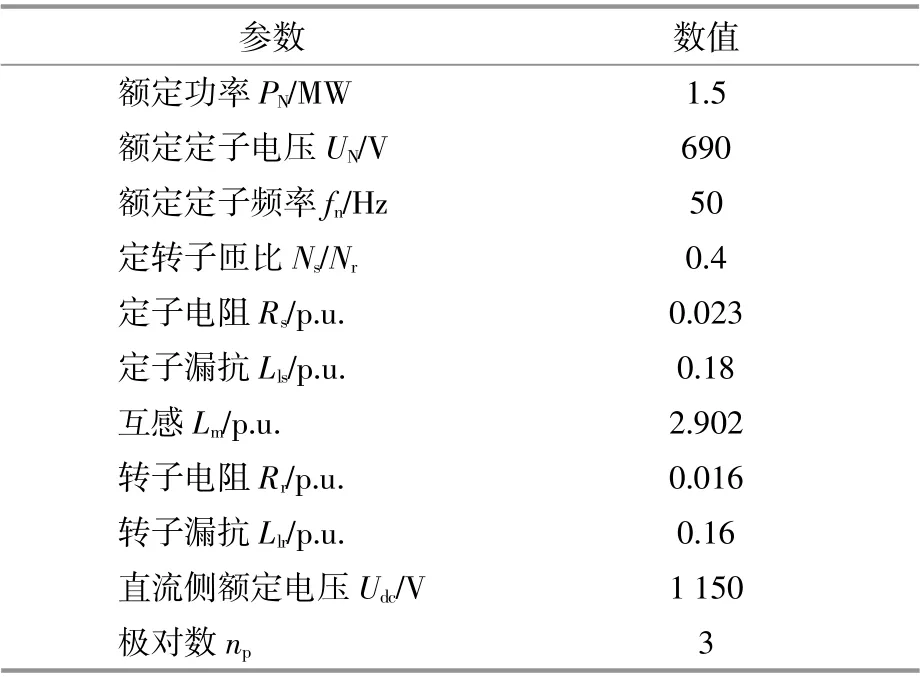
表1 DFIG参数Table 1 Parameters of doubly fed wind turbines

DFIG工作在额定电压条件下，其中，输出有功功率Ps为0.7 p.u.，输出无功功率Qs为0 p.u.，机组转差率为-0.2。在t=1 s时，发生130%的对称电压骤升故障，采用故障检测方法[19]，若检测到电网故障，投入控制策略，持续300ms，故障清除。

4.1 转子电流结果对比

为验证所推导转子全电流表达式的精确性，分别设置DFIG电压骤升幅度为130%和120%。图3和图4所示为对称骤升故障下，基于文献[23]方法搭建的Simulink仿真模型下转子电流波形与采用本文转子全电流计算表达式（5），（7）和（12）绘制的转子电流波形。由图3可知，电压骤升幅度为130%下，转子电流在故障后一个周期最大电流值为2.871 p.u.，计算误差为4.1 %。由图4可知，电压骤升幅度为120%下，转子电流最大值为2.404 p.u.，计算误差为4.9 %，暂态分量衰减较慢。表2为骤升故障下转子电流计算结果对比，可以看出，两种情况的计算结果与仿真结果误差均维持在10%以下，该误差范围能基本满足转子电流计算和分析要求。误差出现的原因是忽略了定子电阻和1/τs的影响以及系统误差。

图3 电网电压骤升130%转子电流波形对比Fig.3 Comparisons of rotor currentwaveforms of 130%voltage surge in power grid

图4 电网电压骤升120%转子电流波形对比Fig.4 Comparisons of rotor currentwaveforms of 120%voltage surge in power grid

表2 骤升故障下转子电流计算结果对比Table 2 Comparisons of rotor current calculations under sudden rise faults

由此可见，本文考虑了控制策略切换延时和无功支持下转子电流指令值的影响，使计算电流值与实际转子电流值相差较小，获得了精确的转子电流暂态表达式，较好地揭示了转子电流变化规律。

4.2 控制策略性能验证

图5为采用文献[23]控制策略，故障后转子电流变化情况。电压骤升故障幅度为130%且300ms后故障切除，按照本文所提控制策略，参考式（15）设计RCR控制器，对L值进行整定，获得转子电流变化波形，如图6所示。在文献[23]控制策略下，转子电流骤升幅度较大，幅值基本超过了2 p.u.，电压穿越效果较差；而本文设计的电流抑制策略能在故障发生30ms后将转子电流维持在安全范围。由于RCR控制器作用，L值突变，转子电流受到扰动，转子电流峰值变大，但在故障发生的很短时间后，转子电流得到抑制，且能在很长一段时间维持在安全范围内。可见，本文控制策略在故障时期的抑制效果明显，比传统只加无功支持的控制策略有着更好的电流抑制性能，且保护了转子变流器等装置，在转子电流抑制上更具优越性。

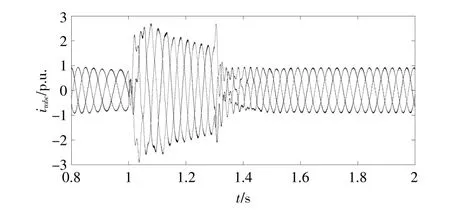
图5 采用文献[23]控制策略故障后转子电流变化Fig.5 Rotor current change after fault under traditional vector control strategy

图6 电流抑制策略故障后转子电流变化Fig.6 Rotor current change after faultunder current suppression strategy

5 结论

针对电网电压骤升故障下转子电流暂态过程复杂，本文提出了DFIG高电压穿越全过程的转子电流计算方法。从DFIG暂态过程出发，推导了骤升故障发生后转子电流的精确暂态表达式，考虑控制切换延时和无功支撑的影响，准确给出了转子电流的计算方法；利用推导后转子电流表达式，设计了一种电流抑制控制方式；最后仿真验证了表达式的准确性和控制策略的有效性，并得出如下结论。

①本文设计的故障后转子电流计算方法，考虑了切换延时和无功支持因素的扰动，反映了故障后电流的变化情况，误差较小，具有较高的准确度。

②本文考虑HVRT准则对于转子电流的要求，取优化后转子电流计算式，提出一种全新的转子电流抑制策略，相比于其他控制策略有着较好的实用性，能有效降低故障后转子电流。