测风塔异常风速数据识别与补齐方法研究

杨 茂，白玉莹

（东北电力大学 现代电力系统仿真控制与绿色电能新技术教育部重点实验室，吉林 吉林132012）

0 引言

风电场历史数据主要包括测风塔气象数据和风机实际功率数据，测风塔气象数据包含风速、风向、气压、温度、湿度等信息，可用来计算理论发电量。将风电场的理论发电量与实际发电量进行对比分析，有利于对风电场的实际发电情况及发电效率进行检测和监察。风速具有间歇性、波动性和随机性[1]～[4]，在实际的风电场运营中，因数据采集通道拥堵或测量环节故障导致风电场数据异常、失真甚至丢失。若直接使用异常数据进行研究，会导致预测结果产生较大误差，严重影响评估结果的准确度[5]。因此，须对测风塔历史风速数据进行筛选识别，并剔除历史数据中的异常值，为后续风电功率预测研究提供优质可靠的数据源。

在异常数据识别与补齐方面，文献[6]提出了组合预测与Bayesian后验比的异常值检测方法，并利用ARIMA方法修正异常风速值，但该方法需要先对风速序列建立组合预测模型，计算过程较复杂。文献[7]分析了异常功率数据产生原因及特点，建立了四分位模型，对异常值进行剔除，根据临近风电场出力具有相似性的特点，采用三次样条多点插值方法补齐缺失数据。但用四分位法识别异常数据，会出现大量被错误识别的数据，且三次样条多点插值方法对数据进行重构精度并不高。文献[8]通过虚拟测风塔技术对测风塔数据进行预处理，但利用了天气预报数据，可能会出现误差累积，并且没有加入校正环节，误识别率较高。

本文充分考虑了测风塔异常风速数据产生原因及特点，提出了一种新型测风塔异常风速数据识别与补齐的方法。该方法首先对4个高度的异常风速数据进行最小二乘滤波处理，得到风速滤波误差后，对其进行肖维勒异常数据识别。由于测风塔不同高度的风速数据都具有一定的关联性，选择相应高度的风速数据对识别结果进行校正，从而提高识别精度，减少误识别率。本文定义了测风塔不同高度风速的属性重要度，按各高度风速的补齐缺失数据，并选择基于马氏距离的相似片段方法，对缺失数据进行重构。实验结果表明，本文所提出的异常数据识别与补齐方法较常规方法识别率更高，补齐效果更好，对不同风电场有一定的通用性，并且使用处理过的风速数据能够提高功率补齐模型的精度。

1 基于最小二乘滤波和肖维勒的异常数据识别方法

1.1 最小二乘滤波

最小二乘滤波法是将输入的原始信号与一个预先假设的含有非周期分量、基波分量和某些整次谐波分量的函数依据最小二乘原则进行拟合[9]。其拟合函数为

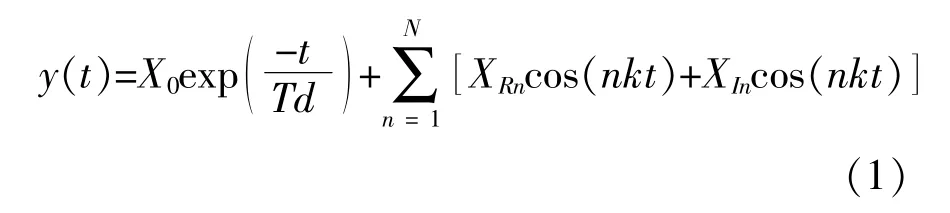
式中：XRn为n次谐波信号的实部；XIn为n次谐波信号的虚部，即XRn=Xncosθn，XIn=Xnsinθn；Xn为信号的幅值；θn为信号的初相角；X0为衰减非周期分量的初始值；Td为时间常数。

考虑到风速序列极少会出现陡升陡降的情况，本文引入最小二乘滤波来平滑原始风速数据，其滤波误差可准确刻画风速骤变的情况，便于后续研究。

1.2 肖维勒异常数据识别

肖维勒异常数据识别准则是指在n次测量实验中，计算数据点误差不可能出现的概率值。其误差不可能出现的概率为

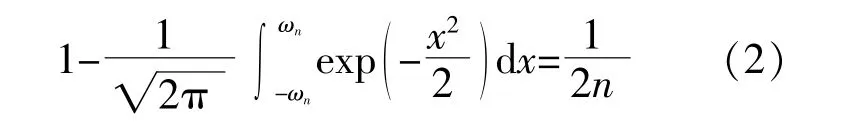
式中：ωn为肖维勒系数，可根据式（2）右端的已知值n，利用标准正态函数表查出。针对某数据xd有：

式中：Vd为数据xd的残差；σ为样本标准差。

肖维勒准则应先计算出待处理数据的平均值和标准差，根据可疑值与平均值之间的差值，选择正态分布函数表，计算给定值处于可疑值的概率，将此概率乘上所选用的数据总数，如果结果小于0.5，则丢弃可疑值。由式（2）可以看出，若采用肖维勒识别方法处理异常数据，该数据应符合正态分布。本文利用该方法，对风速滤波后得到的滤波误差进行肖维勒处理，将超过阈值的部分判定为异常数据，并进行剔除。

1.3 考虑风速波动关联特性的识别结果校正

本文中异常数据识别是在风速不会陡升陡降的前提下，对滤波误差进行肖维勒异常数据识别，但由于肖维勒阈值的设定较为固定，并且难以准确刻画出数据本身产生的剧烈波动，易被误识为风速数据。

考虑到测风塔不同高度的风速数据都具有一定的关联性，若同一时刻只有50m高度的风速出现了陡升或者陡降的情况，而其他3个高度处于平稳波动状态，则该时刻50m高度的风速数据为异常数据。本文选择相应高度的风速数据进行识别结果校正，其表达式为

式中：Eai为待处理高度处第i时刻风速滤波误差；Ebi为对比高度处第i时刻风速滤波误差；wi为滤波差值。

若wi在某一范围内，说明该时刻其他3个高度的风速也有陡升或者陡降的现象，且波动幅度处于正常范围内，则此时的风速数据属于正常波动情况。若超出范围，说明只有当前处理高度的风速出现了陡升陡降，其他3个高度都处于平稳波动状态，则判定该处理高度第i时刻的风速数据异常。

2 基于属性重要度和相似片段的数据补齐方法

2.1 属性重要度

2.1.1 基于属性依赖度的属性重要度

文献[11]利用删除前后属性集的依赖度差，计算属性重要度，即表征了该属性对于整个集合分类能力的贡献大小。其表达式为

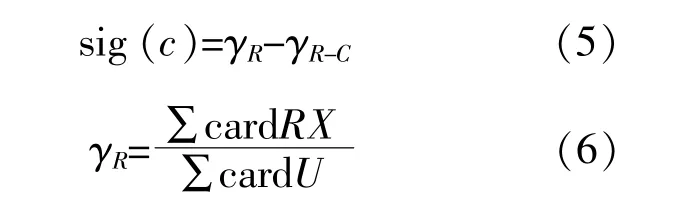
式中：sig（c）为属性C的相对依赖度；card为集合的势；γ为属性的依赖程度；R为所有条件属性的集合，条件属性C∈R；RX为X的近似集。

2.1.2 本文的属性重要度定义

本文属性重要度的计算方法如下。令Si=KKi，i=1，2，3，4，K代表该组数据的最佳聚类数，选取Calinski-Harabasz准则作为确定最佳聚类数的方法，VRCK为准则的量化指标，其表达式为

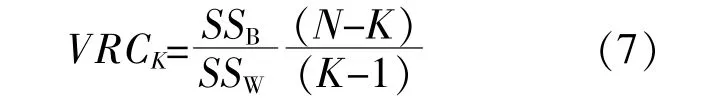
式中：N为该组数据总数；SSB为聚类分组后组与组之间的平方和误差；SSW为聚类分组后组内平方和误差。

由式（7）可以看出，如果组内平方和SSW越小、组间平方和SSB越大，那么聚类效果就会越好，即VRCK值越大，聚类效果越好。确定好最佳聚类数K后，计算Si，按Si大小排序，确定4类数据的属性重要度顺序，Si越大，该类属性对整体数据越重要，影响度越大，则优先补齐该类属性。

2.2 补齐步骤

基于属性重要度的相似片段补齐法，核心思想是按某列数据对整体数据的重要性分先后顺序进行补齐，本文所提识别与补齐算法的流程图如图1所示。

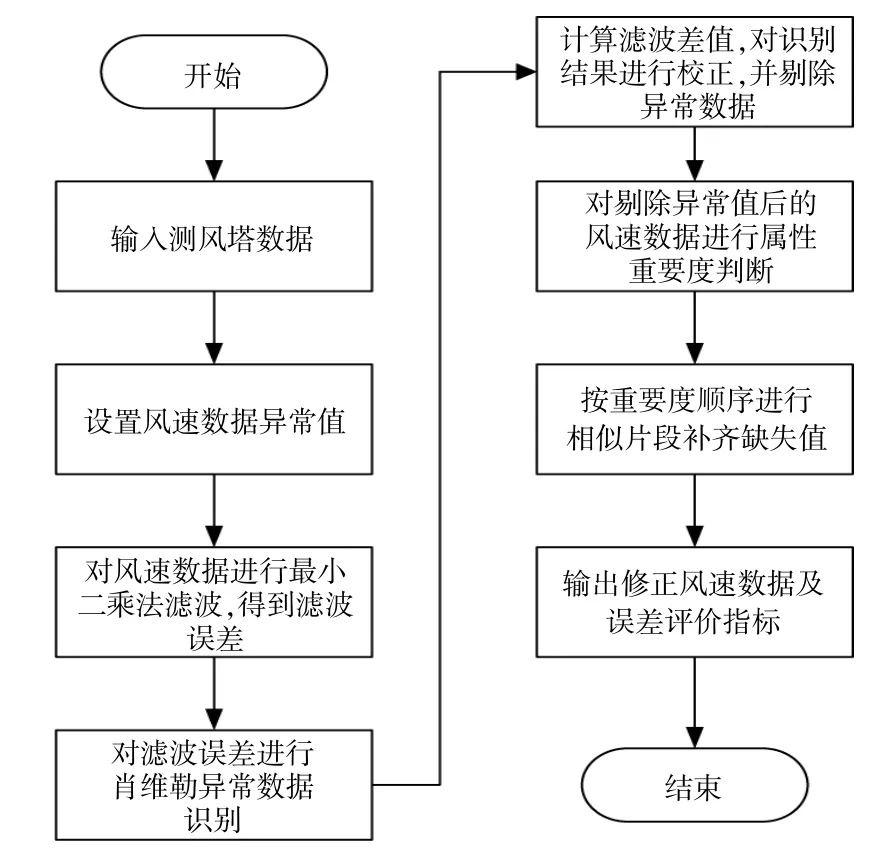
图1 识别与补齐算法流程图Fig.1 Flow chartof identification and completion algorithm

3 评价指标

本文利用总识别率R，正确识别率r与误识别率w 3种指标来对比不同方法的异常数据识别效果。R表示识别出的数据量占总数据量的比值；r表示能够准确识别出的异常数据占总异常数据的比例，能够反映数据识别的效率；w表示误识别的数据个数占总识别数据的比例，能够反映数据识别的准确率。3种评价指标为

式中：nall为算法全部识别出的数据个数；N为数据总数；njud为准确识别出的异常数据个数；n为实际的异常数据个数；nfau为错误识别的数据个数。

对于风速数据补齐效果，每个位置的补齐值及其绝对误差不同，所以将各个补齐位置的绝对误差取绝对值后再求平均值，即选择平均绝对误差（MAE）进行评估，其表达式为

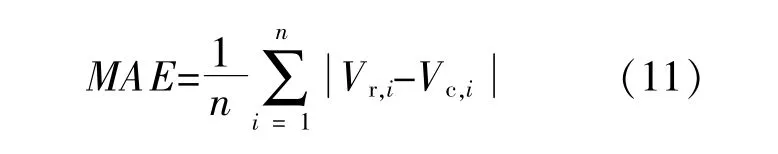
式中：Vr，i为i位置的真实风速；Vc，i为i位置的补齐风速；n为实际异常数据个数。

4 算例分析

为验证本文所提出的测风塔异常风速数据识别与补齐方法的有效性，以东北某两个风电场的测风塔历史风速数据为研究对象，相关信息见表1。其中：A风电场选取2014年2月测风塔4个高度在同一时间段的1 000×4个历史风速数据作为研究样本；B风电场选取2010年10月测风塔4个高度在同一时间段的1 000×4个历史风速数据作为研究样本。考虑到测风塔本身异常数据特性，在每一个高度的1 000个数据中选择100个随机置0作为异常数据。

表1 风电场基本信息Table 1 Basic wind farm information sheet

4.1 异常风速数据识别

本文利用所提模型，对两个风电场测风塔异常风速数据进行识别。图2为A风电场滤波前后10m风速数据及识别结果对比图。

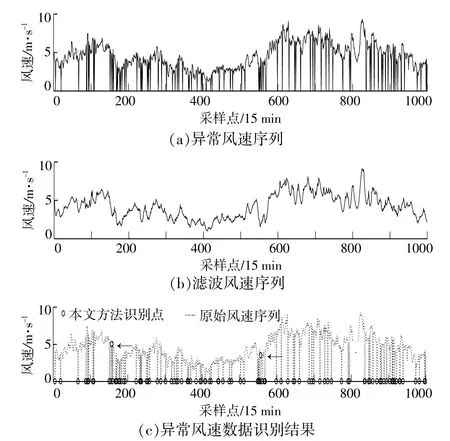
图2 最小二乘滤波前后A风电场测风塔10m风速和识别结果对比Fig.2 Comparison of 10m wind speed and identification results ofwind farm A wind farm wind tower before and after least square filtering

由图2可见，采用最小二乘滤波对原始数据进行处理后，新序列更加平滑，未出现大范围的陡升陡降，方便后续使用数据。在识别剔除异常数据时，由于风速数据并不符合正态分布[12]，直接对其进行肖维勒处理，会出现很多被误识别的数据。本文提出对滤波后得到的滤波误差分布进行拟合，其效果比直接对风速数据进行肖维勒处理好，误识别率低。

4.2 识别结果校正

本文利用A风电场历史测风塔4个高度的风速数据，可得到各个高度与其对比高度的滤波差值范围，数据计算结果见表2。

表2 A风电场各校正高度滤波差值范围Table 2 Range of filter difference for each correction height ofwind farm A

观察wi可知，A风电场中，10～50m和65～80 m风速之间的波动关联度较强，所以本文A风电场选择10m与50m风速数据，65m与80m风速数据互相进行校正。B风电场计算同理，选择10m与30m风速数据，50m与70m风速数据互相进行校正。

由图2可知，与滤波前对比，异常点绝大部分都被识别出来，只存在两个误识别点和一个异常点未被识别。观察两个误识别点的位置（箭头所指位置）都处于大范围陡升陡降区间内，可能因为数据本身存在陡升陡降，其余高度也有陡升陡降，但校正环节计算的滤波差值刚好在区间范围内，所以校正时没有发现；未被识别出的异常点可能是因为该点数据本身存在错误或者陡升陡降不明显，滤波误差较小，导致异常值未识别出来。表3是对两个风电场风速异常数据进行识别剔除后的结果。由表可以看出，滤波误差进行肖维勒处理后，比直接对风速数据进行肖维勒处理准确率高，且加入校正环节之后大大降低了误识别率。

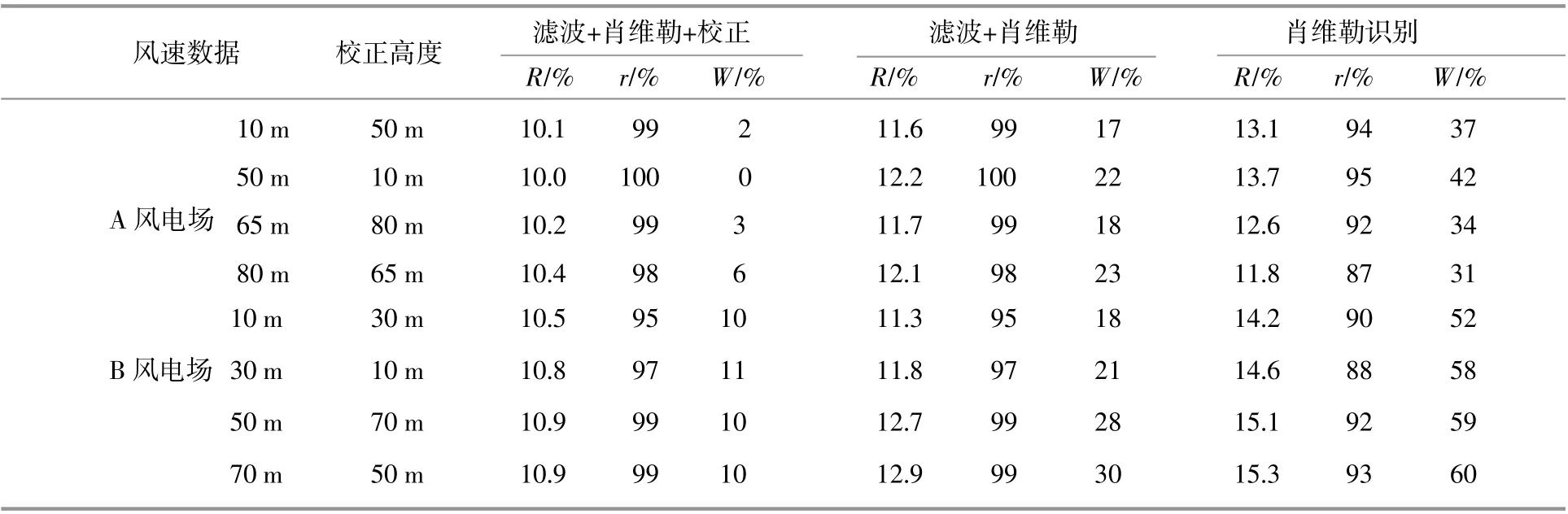
表3 异常风速数据识别结果Table 3 Evaluation table of abnormalwind speed data identification results

4.3 缺失数据补齐

以A风电场为例，利用方差比准则计算出的最佳聚类数k，根据k值得到风速数据属性重要度排序：80 m，65 m，10 m，50 m，即80 m风速对数据集的影响最大。相似片段长度设定根据历史数据试验得出，长度为9时效果最好。同理，B风电场计算风速数据属性重要度排序：70 m，50 m，10 m，30 m，相似片段长度为7时，补齐效果最好。将本文补齐方法与持续法、不考虑属性重要度的相似片段补齐法和灰色关联方法作对比，以A风电场10 m风速为例，利用本文方法的补齐效果如图3所示。

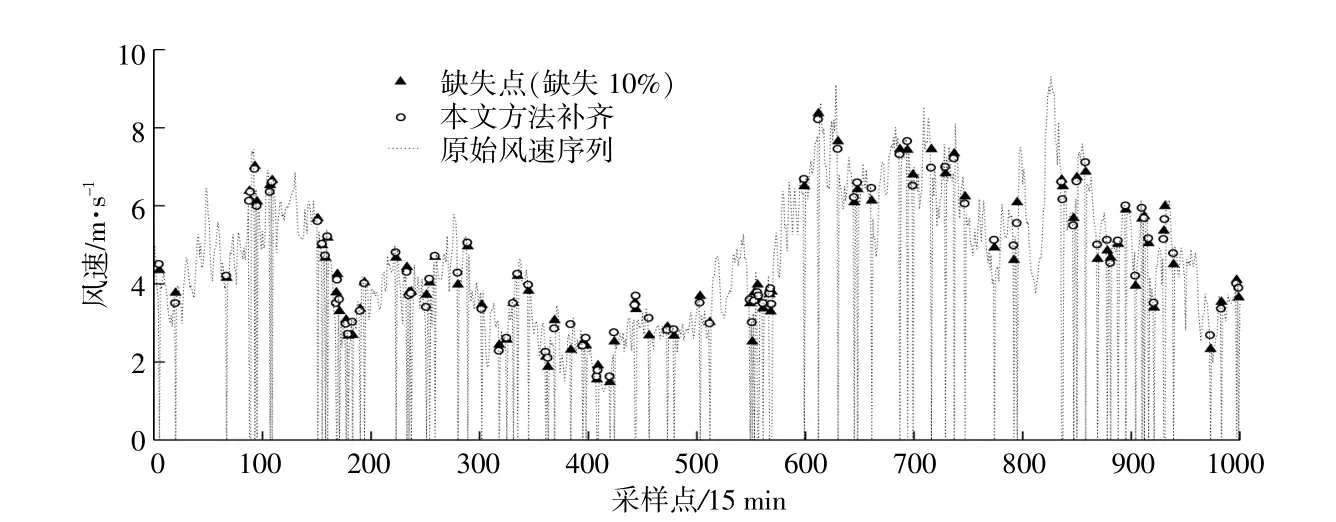
图3 本文方法补齐A风电场10m风速数据效果图Fig.3 Thismethod complements the effectmap ofwind speed data of 10m in A wind farm

表4是针对两个风电场，选择相似片段补齐法、灰色关联补齐方法和持续法与本文所提补齐方法作对比得到的平均绝对误差。 由表4可以看出，对较低的两个高度风速数据补齐的误差普遍要比较高的两个高度风速数据补齐的误差大，这是因为较低的两个高度风速波动较大，曲线毛刺多，而较高的两个高度风速曲线较平滑，用持续法效果也很好。以待补齐时刻为中心，与找相似片段补齐相比，只以一个时刻进行灰色关联补齐效果好；若采用相似片段法进行补齐，应优先补齐对整体风速数据影响较大的某高度风速，从而减小补齐过程中的误差累积。从两个风电场补齐结果来看，A风电场平均绝对误差均小于B风电场，从数据本身分析，其主要原因是A风电场测风数据质量较好。但对于两个风电场，本文补齐方法效果均优于单一方法。

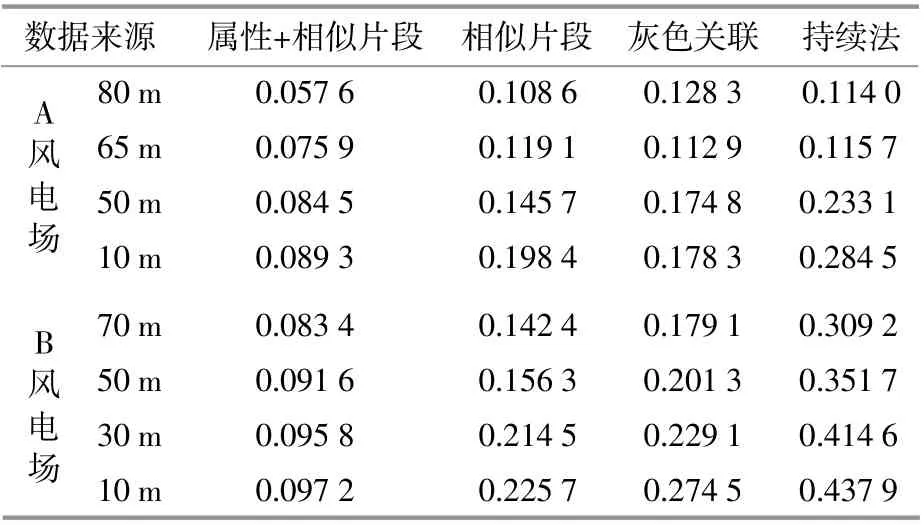
表4 各补齐方法结果Table 4 Evaluationmethod for each complementmethod

4.4 应用分析

为验证对测风塔风速数据进行处理的工程实用价值，本文利用Python平台的Keras深度学习框架，以Theano为后端构建基于LSTM的考虑测风塔信息的整场功率数据补齐模型，数据来源选择黑龙江某风电场测风塔数据和整场功率数据，采样间隔15min，功率数据总量为2 000，缺失率5%，缺失值设置为-200。模型参数如下：模型网络层数为3，各层节点数分别为7，17和1，迭代次数设置为80。

图4为选取一段功率数据直观分析补齐结果。表5为3种补齐方法的MAE值。选择式（11）中的MAE作为评价指标，其中：方法一指使用本文方法处理过的测风塔数据作为LSTM输入进行缺失功率补齐，模型输入为包含缺失值的风电场功率数据、归一化后的测风塔10，30，50m和70 m高度风速及对应风向，模型输出为功率数据的补齐值。方法二为未处理过的测风塔数据作为LSTM模型的输入。方法三为持续法补齐。

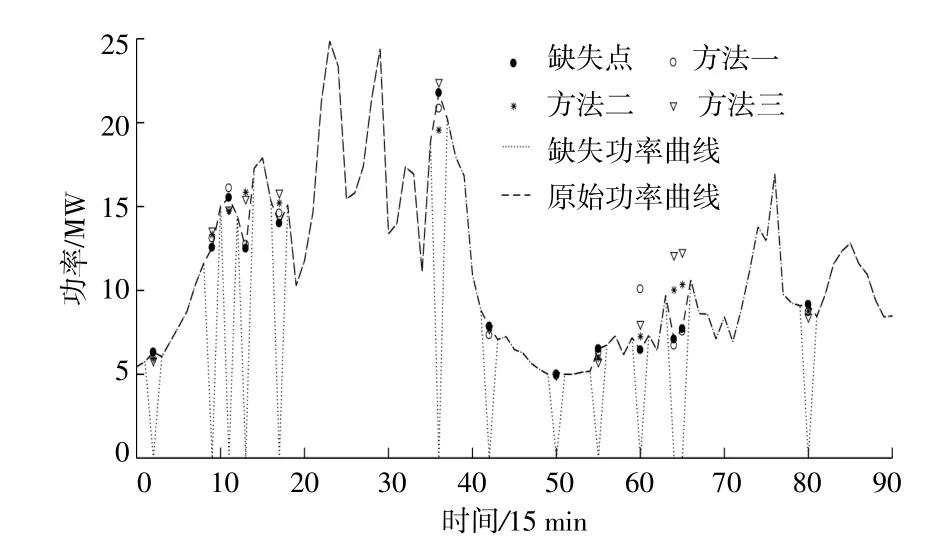
图4 部分功率数据补齐效果图Fig.4 Partial power data fill effectmap

表5 不同输入数据功率补齐结果Table 5 Different input data power completion result evaluation form

由图4和表5可知，使用处理后的测风塔数据作为模型输入，补齐功率缺失数据，可有效提高补齐精度，为后续风电研究提供优质可靠的数据源。

5 结论

风电场测风数据能够真实客观地反映该区域的风能资源情况，且数据质量的好坏对于计算理论发电量有重要意义。本文根据异常风速数据产生原因及特点对异常风速数据进行识别剔除，并在此基础上根据属性重要度和相似片段的方法对缺失的风速数据进行重构。主要结论如下。①提出一种基于最小二乘滤波-肖维勒组合的异常风速数据识别算法，并利用测风塔不同高度风速数据具有波动关联性这一特点，对待剔除数据进行校正，能够提高识别率，减小误识别率。②在数据缺失的情况下，提出一种基于属性重要度-相似片段的数据补齐方法，优先补齐对整体风速数据影响较大的某高度风速，减小误差累积，重构精度高。③算例将本文所提方法与几种常见的异常数据识别与重构方法进行比较，结果表明，本文提出的方法可有效识别异常数据，重构缺失数据，对不同风电场有较强的通用性，并且使用处理过的风速数据能够提高功率补齐模型的精度，具有一定的工程实用价值。