正应力作用下北山花岗岩单裂隙几何特征对辐射流渗流行为的影响研究

范栋珏，赵星光，张海洋，刘 健，刘飞杨

(核工业北京地质研究院，北京 100029)

地下岩体中存在大量的天然裂隙，构成了地下水渗流的潜在通道。地下水渗流可能会导致采掘过程中围岩突水或支护失效。因此，研究裂隙岩体的渗流特性对地下工程安全具有重要意义。地下水在裂隙中的流动形态可分为平行流和辐射流[1]，通常地下水从裂隙一侧向另一侧以平行流方式流动，但对地下工程结构进行开挖时，地下水以辐射流方式从岩体四周流向临空面。因此，辐射流行为是裂隙渗流特性的研究重点之一。

早期，学者们将天然裂隙简化为平行且互相不接触的平板，并将Navier-Stoke方程简化后建立了立方定理[2]。然而，天然裂隙表面粗糙不平，且存在点接触或面接触，其接触面积随应力的增加而增大[3]，若采用传统的立方定理计算将高估裂隙的渗透性能。为了合理描述裂隙渗流行为，许多学者结合室内裂隙渗流试验结果对立方定理进行了修正。王媛等[4]将立方定理的修正方法分为五类：粗糙性修正系数修正法、隙宽密度分布函数修正法、隙宽分布函数直接修正法、节理粗糙度系数JRC修正法以及面积接触率修正法；还有学者[5-8]通过引入等效水力隙宽、平均隙宽、力学隙宽等参数，减少了立方定律带来的误差。此外，许多学者[6,9-15]针对裂隙力学隙宽与等效水力隙宽，结合接触面积、隙宽分布影响系数建立了相应的裂隙渗流计算模型。然而，这些计算模型中采用的隙宽分布影响系数并不能完全表征裂隙内隙宽大小及其非均匀分布对裂隙渗流特性的影响。

对于单裂隙辐射流，BARKE[1]建立了广义辐射流(GRF)模型，描述了常用液压测试形式中的水头变化；CAO等[16]针对辐射流平行板模型提出了修正的立方定率公式，减小了由立方定理计算带来的误差。 然而，目前关于裂隙辐射流渗流特性研究较少，特别是对于辐射流条件下的渗流计算模型鲜有研究。 因此，本文根据裂隙形貌扫描结果，采用地质统计学中变异函数理论对裂隙空隙三维分布进行量化表征。同时，考虑裂隙空隙三维分布特征和接触率为影响因素，提出辐射流等效水力隙宽计算模型，并使用MTS815岩石力学试验系统对裂隙岩样进行不同正应力下的渗流试验，验证计算模型的合理有效性。

1 裂隙渗流特性试验研究

1.1 岩样加工制备

岩样取自我国高放废物处置库北山预选区新场岩体BS33号钻孔附近浅地表。首先，加工4个直径为100 mm、高度为100 mm的圆柱形岩样；然后，将岩样放入劈裂装置中(图1(a))，采用压力机以1 500 N/s的加载速率对岩样进行劈裂，形成人工裂隙；最后，采用水射流切割设备在下部岩样中心打一个小孔，作为平面径向流的中心进水边界，在上部岩样距离侧面边界8 mm处均匀打一圈小孔，并沿小孔打出与界面同心的圆形沟槽作为出水边界(图1(b))。

图1 裂隙岩样示意图Fig.1 Schematic diagram of fracture specimen

1.2 试验方法

采用MTS815岩石力学试验系统对裂隙岩样进行不同正应力下的辐射流试验(图2(a))。首先，使用硅胶密封裂隙岩样的侧缝(图2(b))，待硅胶干燥后利用热缩管将岩样与试验机压头紧密包裹，并将轴向引伸计安装于岩样中部测量裂隙加载过程中的变形(图2(c))。 随后，对岩样施加10 MPa围压，以有效避免水从岩样侧壁与热缩管之间的缝隙内流动。 最后，采用不同的正应力(11 MPa、15 MPa、20 MPa、30 MPa、40 MPa、50 MPa、60 MPa)对岩样进行分级加载，加载过程如图3所示。 分别在每一级荷载作用下采用稳态法测量辐射流流量。 在试验过程中，进水口与出水口水压差恒定为1 MPa，进口流量、出口流量由活塞泵位移与稳定渗流时间计算获得。

图2 渗流试验设备及岩样安装Fig.2 Seepage test equipment and a typical specimen setup

图3 正应力加载过程Fig.3 Normal stress loading process

1.3 岩石裂隙渗流特性分析

根据上述试验方案，获得了不同正应力作用下水在裂隙岩样中的流量变化，如图4所示。由图4可知，在正应力为11～60 MPa范围内，所有岩样流量随正应力的增大表现出相似的变化规律，即流量随正应力的增大而减小，且其衰减速率随正应力增加而减小，表明水在裂隙中的流量变化对低正应力条件(<20 MPa)较为敏感；当正应力大于50 MPa时，各岩样流量值的差异性不再显著。此外，在相同正应力条件下，岩样3的流量显著高于其他岩样，即裂隙内部几何特征存在差异性，致使其表现出了不同的渗流特性。因此，本文对裂隙空隙三维分布进行分析和表征，查明裂隙内部几何特征对其渗流性能的影响规律。

图4 裂隙岩样流量随正应力的变化Fig.4 Variations of flow quantity with normal stressfor the fracture specimens

2 裂隙内部几何特征量化表征

岩石裂隙中存在大量空腔及接触域，它们是影响裂隙渗流特性的关键因素。根据HAKAMI[17]的研究，裂隙内部几何特征主要包括裂隙隙宽、裂隙接触区域、裂隙内部空隙三维分布等。其中，裂隙隙宽可由等效水力隙宽、平均隙宽、力学隙宽等参数进行表征[5-8]，裂隙接触区域可由接触率进行表征。 然而，对裂隙内部空隙三维分布特征表征参数的研究较少。PYRAK等[18]对裂隙内部的隙宽分布进行研究，发现裂隙隙宽分布通常服从正态分布或对数正态分布，但其分布函数无法表示裂隙连通以及裂隙非均匀变化对渗流的影响；陈跃都[19]采用相对分形维数对裂隙隙宽的分布进行表征，但其使用的盒子计数法不适用于圆柱形的辐射流试件。因此，本文根据裂隙面扫描结果，采用变异函数理论对裂隙空隙三维分布特征进行表征，并结合裂隙力学隙宽和接触率参数，对裂隙内部几何特征参数进行量化表征。

2.1 裂隙面形貌特征扫描

为了获得裂隙面的形貌特征，在试验前后采用OKIO-5M三维形貌扫描仪对裂隙面进行扫描(图5(a))，扫描精度为10 μm，典型扫描结果如图5(b)所示。通过三维点云处理软件，采用克里金法[20]将获得的裂隙面三维点云离散在x-y平面上形成等间距的规则点云，并将裂隙上下表面的点云坐标划分成规则网格，且上下裂隙面网格相互对应，以便对裂隙几何特征参数进行计算。随后，采用点云拼接法[18]计算裂隙各网格点处隙宽ei，定义裂隙隙宽ei≤0的网格点为接触点，裂隙隙宽ei>0的点为空隙点，即可获得裂隙间的空隙及接触域的分布大小。

图5 三维形貌扫描设备及裂隙典型扫描结果Fig.5 3D shape scanner and typical scanning results

2.2 裂隙空隙三维变异函数计算

作为地质统计学的基本工具，变异函数既能描述区域变量的空间结构，也能描述其随机性。变异函数r(h)定义为区域化变量的增量平方的数学期望，即区域化变量的方差[21]，见式(1)。

2r(h)=E{[Z(X+h)-Z(X)2]}

(1)

式中：h为数据点间距离；Z(X)、Z(X+h)分别为空间某点位置X和与之相距h的两个区域变化量。

将扫描获得的裂隙间空隙ei作为区域变量即可计算裂隙隙宽分布变异函数。由于辐射流条件下，裂隙内流体流动方向存在不确定性，可用三维经验变异函数r*(h)[22]进行估算，即以h为相隔的任意对点的隙宽值[e(xi+a,yi+b)，e(xi,yi)]间增量平方的算数平均值进行计算，见式(2)。

(2)

式中：N(h)为有效数据对数；e(xi,yi)为点云在(xi,yi)处的隙宽值；a、b为h在x方向、y方向上的分量，即a2+b2=h2。

为获得裂隙隙宽的变异特征，并对裂隙隙宽的三维分布进行统计计算，需要对变异函数散点图进行拟合，进而获得变异函数的理论模型及其参数。常见的变异函数理论模型有球状模型、指数模型、对数模型等。利用式(2)获得岩样1在无应力状态下裂隙隙宽变异函数曲线如图6所示。

图6 变异函数曲线Fig.6 Variogram curve

从图6中可以看出，曲线前段增长较快，中后段水平上下波动，可选取球状模型(式(3))进行拟合。

(3)

需要说明的是，变异函数出现第一个峰值点之后的数据是大于变程a的数据，与函数拟合无关[23]。因此，拟合对象仅选择变异函数的第一个峰值点之前的r*(h)值。

2.3 裂隙内部几何特征量化表征参数计算

获得裂隙空隙的变异函数拟合曲线后，即可采用相关参数对裂隙空隙的三维分布特征进行表征。变异函数球状模型主要参数有变程a、基台值C和块金系数C0。 获得的块金系数C0一般较小，在0左右波动，对变异函数形式影响不大，因此不作考虑。基台C表示隙宽随空间变化的幅度，通常基台C越大，隙宽随空间变化幅度越大。 变程a表示隙宽随空间变化的频率，通常变程a越大，隙宽随空间变化的频率越大，隙宽变化曲线就越平缓。 因此，裂隙隙宽的不均匀程度与基台C成正比，与变程a成反比。本文提出裂隙空隙的三维分布系数CA来对裂隙空隙的三维分布特征进行量化表征，其表达式见式(4)。

CA=C2×a-1

(4)

由式(4)可以看出，裂隙空隙的三维分布系数CA值较大时，基台C或变程a的值较大，此时裂隙空隙随空间的分布不均匀。当CA=0时，裂隙上下表面完全平行，裂隙空隙均匀分布。

根据裂隙面扫描结果，采用点云拼接法[19]计算裂隙在不同应力作用下力学隙宽en和接触率ω。以力学隙宽en为空间变量，采用变异函数理论获得基台C与变程a，并根据式(4)计算裂隙空隙的三维分布系数CA，见表1。

表1 变异函数计算结果Table 1 Fitting results of average aperture

3 辐射流渗流模型建立

目前，单裂隙渗流的研究重点是针对裂隙力学隙宽与等效水力隙宽建立相应的计算模型[6,9-15]，其中应用最为广泛的为YEO[14]建立的模型，见式(5)。

(5)

式中：为裂隙隙宽的平均值，m；s为裂隙隙宽的标准偏差；ω为裂隙的接触率。

YEO模型中(1-2.4ω)和[1-1.5(s/)2]分别代表接触率和裂隙隙宽对裂隙水力学开度的影响。然而，该模型中的裂隙隙宽标准偏差s仅代表裂隙隙宽分布的分散程度，并不能完全表征裂隙内隙宽大小及其非均匀分布对裂隙渗流特性的影响。同时，该模型夸大了裂隙接触率对水力隙宽计算的影响。例如，当裂隙接触率大于0.416时，其接触率影响系数(1-2.4ω)小于0，导致裂隙等效水力为负值，即表明裂隙不具有渗透性，与实际不符。

因此，本文在YEO模型的基础上，对其接触率影响系数进行修正，并使用力学隙宽和空隙三维分布系数来代表裂隙隙宽及对其三维分布的影响，提出了CA计算模型见式(6)。

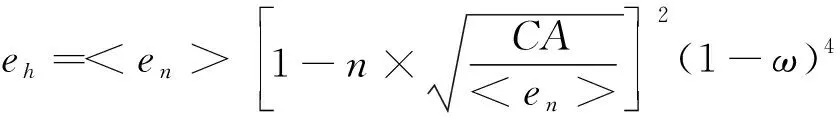
(6)

式中，n为试验拟合参数，对于本试验采用的北山花岗岩裂隙岩样，n=5.9。

为验证CA模型的有效性，将表1中裂隙几何特征参数代入式(6)，获得等效水力隙宽值。随后，采用立方定理计算裂隙流量。考虑到辐射流的扩散特性，使用辐射流立方定理计算[14]，见式(7)。

(7)

式中：Q为流体流量，m3/s；r0和r1分别为岩样内圈半径和外圈半径；ΔH为水头差，m；ν为水的运动黏度，m2/s。将裂隙流量实测值与CA模型计算值进行对比，如图7所示。

图7 各岩样CA模型计算值和试验结果对比Fig.7 Comparison of calculated values of CA models and test results for different samples

从图7中可以看出，采用CA模型获得的裂隙等效水力隙宽与实测值较为接近，由此表明该模型可以合理地描述裂隙几何特性对裂隙渗透特性的影响。此外，对于线性达西渗流而言，其渗透率k与水力隙宽eh存在定量关系，见式(8)。

(8)

将式(6)代入式(8)可得渗透率的几何特征定量表达式，见式(9)。

(9)

对于光滑平行板模型，其接触率ω和裂隙连通空隙三维分布表征系数CA均为0，此时eh=en,式(9)便可简化为式(8)。需要说明的是，该模型的所有参数是在室内岩样尺度上获得，对于其尺寸效应还需进一步研究。

4 结 论

1) 水在裂隙岩样中的流量随正应力的增大而减小，且其衰减速率随正应力增加而减小。

2) 基于变异函数理论对裂隙空隙三维分布进行量化表征，建立了辐射流等效水力隙宽计算模型(CA模型)。该模型考虑了裂隙几何特征对裂隙渗透特性的影响，可定量表征正应力作用下裂隙等效水力隙宽与力学隙宽、凸起接触率和空隙三维分布系数之间的函数关系，模型计算结果与试验结果具有较好的一致性。

由于室内试验条件的限制，本文尚未对更大尺寸的岩石裂隙进行试验。此外，现有手段也无法获取流体在裂隙内的流动轨迹。因此，裂隙辐射流的尺寸效应及渗流轨迹对其渗流特性的影响是下一阶段的研究重点。