旋转二次曲面透镜基点研究

徐海斌 顾菊观

(湖州师范学院理学院 浙江 湖州 313000)

1 引言

透镜在光学教学和光路设计中的应用非常普遍[1,2].透镜参数的选择在很大程度上影响了其效果.因此，对透镜特性的研究具有着重要的意义.

透镜基点位置是描述透镜特征的重要参数.现有光学教材往往只对球面透镜进行阐述，给出傍轴近似下基点位置参数的公式.玻恩在《光学原理》一书中对旋转二次曲面的几何光学成像问题进行了初步探讨，但是并没有给出其具体形式[3].在实际光路设计中，非球面透镜因为其较多的优势，得到了广泛的研究与应用[4～6].基于非球面透镜应用的仿真研究也得到了广泛的开展[7～11].基于几何光学基本原理及二次曲面的数学描述[12]，一些研究者对二次曲面透镜参数进行了理论研究，并在各种近似下给出其基点位置描述公式及成像特征[13～15].由于实际透镜加工的限制和测量的不便，使得这些研究结论并没有得到明确的实验验证.同时，现有研究很大程度仅仅考虑曲面顶点曲率半径对基点参数的影响.而二次曲面conic系数是描述旋转二次曲面特征的重要参数.因此，考虑二次曲面conic系数对透镜基点参数究竟会产生怎么样的影响就变得非常有必要.

作为虚拟仿真软件，TracePro具有简单便捷、容易入门、结果可靠直观、能实现图形显示及可视化操作等优点.该软件一个重要特点就是其利用几何光学的基本原理，采用了光线追迹的方法，对每条光线在光学器件中的传输进行仿真演示.这种虚拟仿真所取得的效果，可以避免傍轴近似所带来的偏差，同时也可以有效克服几何光学实验观察条件限制的不足.以对称旋转二次曲面会聚透镜为例，利用该软件对其进行了虚拟仿真.仿真结果实现了对傍轴近似条件下透镜基点位置描述公式的验证，并对二次曲面conic系数和入射高度对基点位置、焦距及其变化率的影响进行了分析，为具有不同conic系数旋转二次曲面透镜成像的光线选择提供一定的参考.该虚拟仿真方法同样适用于自由曲面透镜特性的研究[16].

2 旋转二次曲面透镜

2.1 基本结构

旋转二次曲面包括最常见的球面、抛物面、椭球面和双曲面，其中conic系数决定了二次曲面的面形.旋转二次曲面的标准面面形公式可以表示为[12]

(1)

图1 旋转二次曲面透镜结构示意图

2.2 旋转二次曲面透镜的基点

对于任意一个旋转二次曲面，假定其左右两侧介质折射率分别为n0和n，则其焦距可以表述为[13]

(2)

对于具有图1的透镜结构而言，可得A界面和B界面的焦距分别为

(3)

(4)

图1中A和B两个界面顶点之间的距离为d，则两层界面之间的光学间隔为

Δ=d-f′A+fB

(5)

(6)

(7)

(8)

由上述透镜基点位置公式并结合图1可以看出，基点位置与二次曲面透镜的conic系数并没有关系.这是在推导上述关系时，进行了一些近似有关.因此，很有必要对不同conic系数下透镜的基点位置进行观察，寻找conic系数对透镜基点位置变化的影响.

3 旋转二次曲面透镜建模及基点位置分析

利用TracePro软件可自由建模二次曲面透镜.对称或非对称旋转二次曲面透镜均可采用同样的建模方法进行仿真研究.为简单直观，这里主要采用具有固定参数的对称旋转二次曲面透镜结构进行仿真研究.

3.1 不同conic系数的曲面特征

现有理论研究结果并没有考虑二次曲面的conic系数对透镜的影响.图2给出了在相同的顶点曲率半径下不同conic系数所对应曲面在yOz平面上的截面图.随着conic系数从1逐渐变化到-1.5，可以发现旋转二次曲面逐渐趋向平坦，因此，conic系数的不同必然会影响光线在曲面折射的效果.这一点尤其是在入射高度较大时，将会变得更加明显.conic系数与典型的旋转二次曲面有一定的对应关系.当k>0时，对应横椭球面；k=0对应球面；0>k>-1对应竖椭球面；k=-1对应抛物面；k<-1对应双曲面.

图2 不同conic系数旋转二次曲面在yOz平面上的截面图

3.2 旋转二次曲面透镜的基点位置

TracePro软件是追迹光线在各种材料及光学器件内传输的几何演示.根据基点的定义，可以找出各种入射高度下基点的几何位置，并给出其变化规律.一方面可以验证理论公式计算的可靠性，另一方面，由于理论公式的推导是基于傍轴近似下的结果，通过利用软件虚拟仿真，可以进一步考查实际基点位置的修正.

图3展示了在虚拟仿真中寻找透镜像方基点位置的示意图.

图3 像方基点位置示意图

3.3 旋转二次曲面透镜基点位置虚拟仿真

为便于比较，仿真实验仅仅对具有相同顶点曲率半径，不同入射高度和不同conic系数下基点位置进行分析.当透镜其他相关参数发生变化时，可以使用同样的虚拟仿真方法进行分析.

当conic系数和光线入射高度发生变化时，透镜的主点位置及其变化率随之发生了变化.从图4(a)可以看出，主点位置随光线入射高度发生较为明显的变化，而对conic系数并不是非常敏感.当光线入射高度越来越小时，像方主点位置趋于理论计算值.图4(b)给出了主点位置变化率随conic系数及光线入射高度的变化特性.当入射高度低于10 mm时，不同conic系数的旋转二次曲面透镜主点位置变化率均小于1%.随着入射高度的增加，其主点位置变化率迅速变大，与conic系数的大小关系不大.图4显示了主点位置及其变化率主要与光线入射高度有关.

(a) conic系数发生变化时主点位置iH变化率随入射高度的变化

(b) conic系数发生变化时主点位置iH变化率随入射高度的变化

透镜焦点位置及其变化率随conic系数和光线入射高度的变化如图5所示.图5(a)中透镜焦点位置随conic系数和光线入射高度变化明显.随着光线入射高度逐渐增加，焦点位置逐渐向透镜靠拢.conic系数越大，这种变化就越明显.当入射高度逐渐减小，不同conic系数的透镜焦点都逐渐趋于理论计算值.图5(b)给出了焦点位置变化率随conic系数及入射高度的变化关系.当入射高度较大时，conic系数越大，焦点位置变化率越大.随着入射高度的减小，焦点位置变化率逐渐趋向于零.图5显示了焦点位置及其变化率与光线入射高度及conic系数有关，并且入射高度越高，conic系数越大，这种变化就越明显.

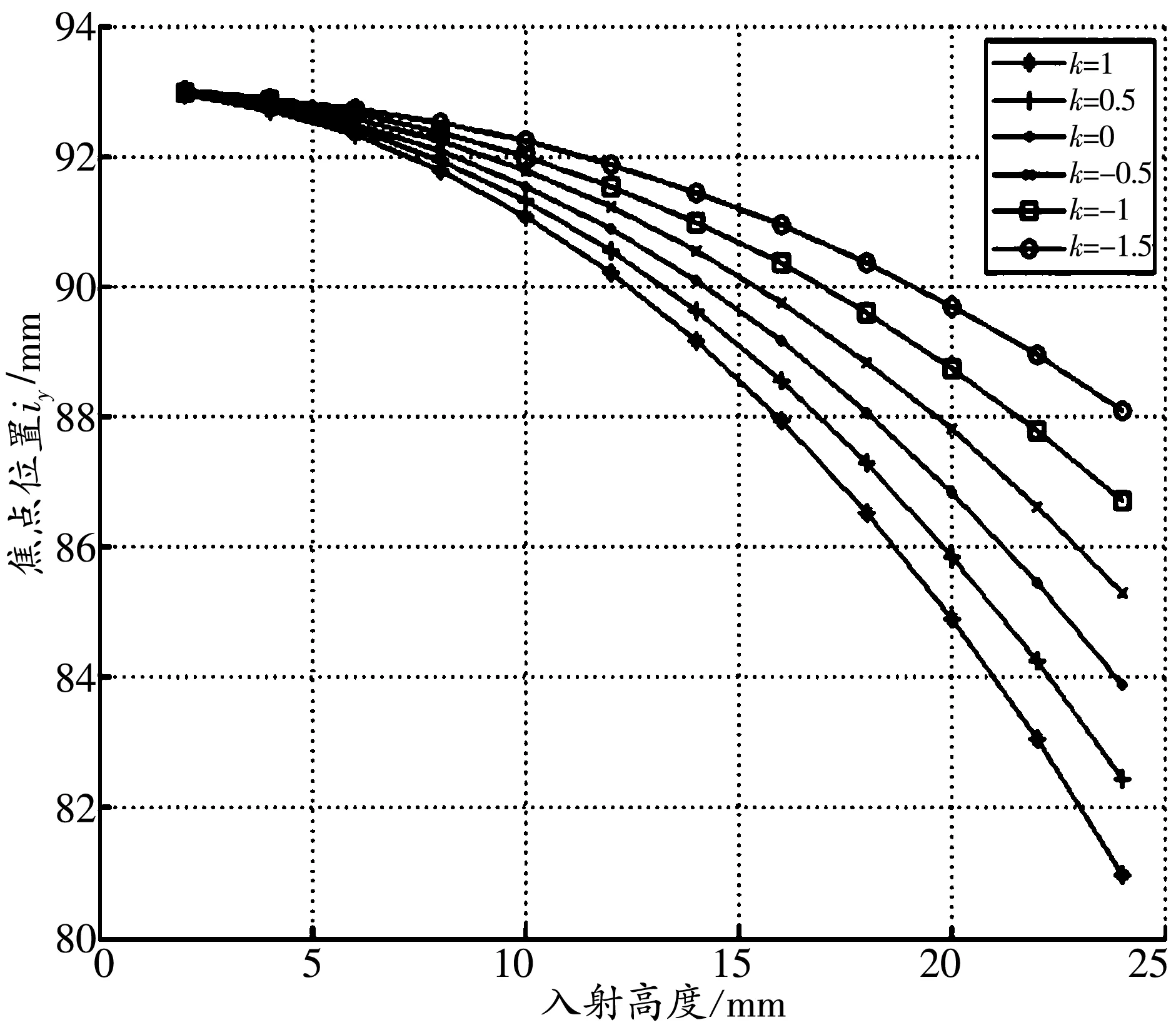
(a) conic系数发生变化时焦距位置iy随入射高度的变化

(b) conic系数发生变化时焦距位置iy变化率随入射高度的变化

透镜焦距及其变化率随conic系数和光线入射高度的变化如图6所示.

图6(a)显示随着入射高度和conic系数的变大，焦距逐渐减小.当入射高度减小时，焦距逐渐趋向理论值，与conic系数无关.

图6(b)显示了焦距变化率随入射高度及conic系数的变化规律.焦距变化率随着入射高度及conic系数逐渐变小，直至趋向于0.图6显示了焦距及其变化率与入射高度及conic系数有关.

通过对图4、图5和图6的分析可知，对于顶点曲率半径相同，不同旋转二次曲面conic系数的透镜在光线入射高度较低时，基点参数与理论计算值基本一致，并且其变化率也较小.当入射高度逐渐增加时，透镜主点位置及其变化率与conic系数关系不大；透镜焦点、焦距及其变化率受conic系数影响较大，conic系数越大，这种变化越明显.

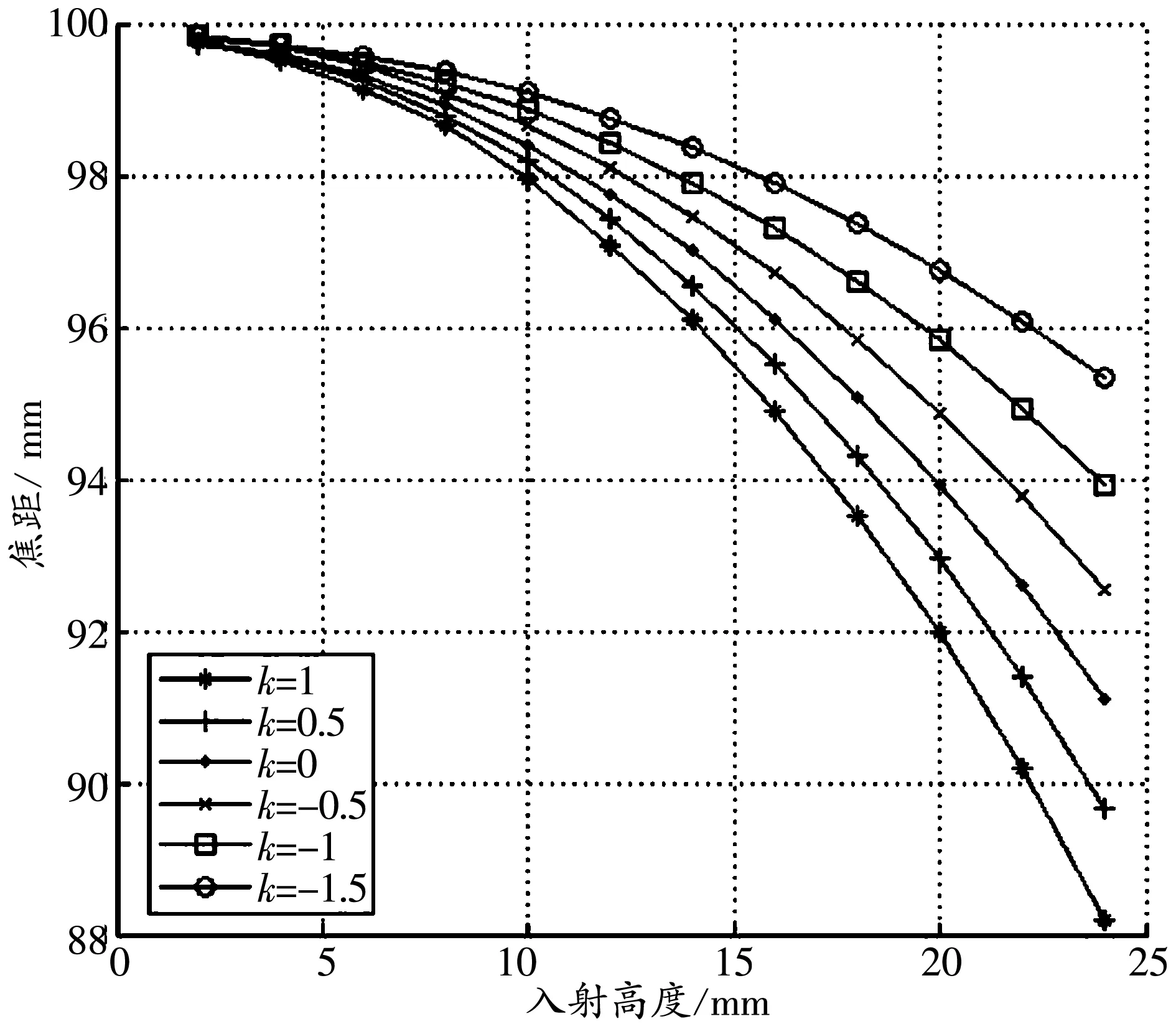
(a)不同conic系数下焦距随入射高度的变化

(b)不同conic系数下焦距变化率随入射高度的变化

4 结论

通过对旋转二次曲面透镜的分析，给出了旋转二次曲面透镜基点位置的计算公式.提出了一种验证透镜基点位置及其变化率的虚拟仿真方案.基于TracePro软件的虚拟仿真结果显示，对于光线入射高度较低的情况下，透镜基点位置的计算公式符合较好.对于光线入射高度逐渐增加时，透镜的主点位置及其变化率主要由入射高度决定，与conic系数关系不大；焦点位置、焦距及其变化率不但与光线入射高度有关，而且与conic系数有关.论文研究结果为透镜成像过程中的光线选择，尤其针对大口径，conic系数不同的二次曲面透镜的光阑选择，提供了定性的参考.该实验方案也可为各种自由曲面的理论参数分析提供一种有效的验证方法.

该虚拟仿真分析方法为不便于实际测量参数的透镜等光学器件测试和光路设计提供一条有益的思路，可拓展大学物理光学教学中球面透镜的教学内容，使得学生对非球面透镜的特征具有更加形象具体的认识.