均匀带电半球面轴线上场强的计算*
白春华 高国明 文丽敏
(云南大学地球科学学院 云南 昆明 650500)
1 均匀带电球面和半球面电场强度的相关计算
电磁学教学中电场强度的计算是一个重要且基础的问题.有关电场强度的计算可以总结归纳出几种常用方法[1,2]:(1)场强叠加原理;(2)高斯定理;(3)电场和电势的梯度关系.上述各种方法中,场强叠加原理是求解电场强度最基本的方法,适用于求解各种电荷分布的带电体的场强分布;高斯定理在求解电荷分布具有高度对称性(球对称、轴对称、平面对称)的几何体的电场时非常简便.除此之外,还可以利用电势和电场强度的梯度关系先求电势再求电场分布.近年来,学者们对均匀带电球面电场的求法以及能否求解球面上的电场进行了反复分析和讨论[3~6].由于不能把高斯面取在带电表面上,所以面上的场强不能由高斯定理直接求出.虽然均匀带电几何面两侧的场强会发生跃变,但面上的电场强度也有唯一的确定值.
我们在教学中发现,当遇到所求问题为均匀带电球面、圆柱面、多层同心球面、同轴柱面等,学生利用高斯定理很容易就能求解出空间电场的分布,但对半球面电场该如何求解并不是很清楚.因为半球面上的电荷分布没有整个球面那样高度的球对称性,所以我们不能利用高斯定理求解.一般而言,适用球面电场的计算方法大多适用于计算半球面的电场.张晓燕等根据叠加原理求解了均匀带电半球面底面上的电势分布和电场强度[7].何海卫等分析了均匀带电半球壳轴线上的电场及其增减性[8].林建福先利用积分法求出均匀带电半球面轴线上的电势表达式,然后利用电场强度与电势的关系导出均匀带电半球面轴线上的电场强度[9].王世芳等利用圆环带法、电势梯度法等多种方法求解均匀半球面球心处的电场强度[10].
上述研究利用多种解法给出了均匀带电半球面的电场强度.作为一种补充,下面我们直接利用库仑定律和场强叠加原理,通过球面积分的方法计算均匀带电半球面在球心、球面上以及球面内外的电场分布,并给出电场分布的E-z曲线.
2 用场强叠加原理计算均匀带电半球面轴线上的电场强度
【例题】设均匀带电半球面电荷面密度为σ,半径为R,求半球面轴线上电场强度的分布.
2.1 均匀带电半球面在球心处的电场强度
取如图1所示的xyz坐标系,半球面位于z轴正半轴.场点P点为半球面轴线上一点,当P点取在球心O处时,在半球面上任取一面积元dS.

图1 半球面球心处的电场
dS=R2sinθdθdφ
面积元dS所带电荷量dq=σdS,在球心O处所产生的场强为
由对称性分析可知,dE垂直于z轴方向的分量相互抵消,沿z轴方向的分量为dEz.
(1)
球心处电场强度的方向沿z轴负方向.
2.2 均匀带电半球面轴线上一点P(0,0,z)的电场强度
图2为场点P位于z轴上不同位置的几种情况.
(1)若0 图2 均匀带电半球面P点处的电场 (2) 采用换元法,令 t2=R2-2Rzcosθ+z2 (3) 由式(3)可得 对式(3)两边分别求导得 tdt=Rzsinθdθ 代入式(2),得 (4) 该电场强度的方向沿z轴的负方向. (2)若z>R,场点P位于半球面外 (5) 该电场强度的方向指向z轴的正方向. (3)当z=R,即P点在半球面上时 (6) 场强方向沿z轴正方向. (4)若0>z>-R,场点P位于球内z轴负半轴,则 (7) (8) 电场强度的方向指向z轴的负方向. (5)若z<-R,被积函数与式(7)形式相同,在z=-R上没有电荷,场强在这点连续,场强表达式与式(8)相同,只是z的取值范围不同. (9) 该电场强度的方向沿z轴的负方向. (6)当z=-R,P点在z轴负半轴与球面交点上 (10) 场强方向沿z轴负方向. 综上,均匀带电半球面轴线上的电场强度分布为 图3是用Matlab软件模拟的均匀带电半球面轴线上的电场强度E随z变化的曲线. 图3 均匀带电半球面轴线上的E-z曲线 对于均匀带电的半球面来说,电荷分布不像整个球面电荷那样高度对称分布,不能用高斯定理求解.其他求解的方法也有多种,最基本的方法还是利用场强叠加原理,再通过面积分求出带电半球面轴线上的场强大小.类似的方法包括分割圆环带法、电势梯度法等.虽然这些解法稍有不同,最终都可归为场强叠加方法的运用.当然,直接用场强叠加原理求解计算量相对要大些,但这种方法适用性最广.同样的解题思路也适用于求解均匀带电球冠电场强度等相关问题.



3 分析与结论

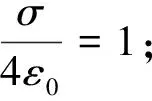
4 总结

