脉冲线性Hamilton系统的Lyapunov不等式

孙月琴，申建华

(杭州师范大学理学院，浙江 杭州 311121)

0 引言

考虑具有脉冲强迫的一阶线性Hamilton系统

(1)

其中N为正整数集.假设系统(1)满足如下条件：

i)脉冲时间序列{tk}是严格单调递增的；

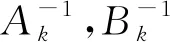
称2n维向量值函数(x(t),y(t))是(1)的一个解，如果它满足(1)，在每个tk是左连续的且存在右极限.当(1)是一个连续系统，即所有的Ak=I且Bk=0时，(1)退化为连续线性Hamilton系统

(2)

或

X′(t)=JH(t)X(t),t∈R,

H(t)为局部可积矩阵值函数

近几十年来，有许多文献研究了连续Hamilton系统的Lyapunov不等式，也已有对于不连续动力系统Lyapunov不等式的研究工作，但结果还不多.有关不连续动力系统的一般理论可参见文献[1].在此，仅列举与本文密切相关的部分研究工作.在2012年，Tang等[2]讨论了系统(2)的Lyapunov不等式，得到了下面的定理1和定理2.

C*(t)≥C(t),∀t∈R,

有Lyapunov不等式

(3)

其中

这里，矩阵测度μ(·)的定义见下节.

(4)

其中C+(t)是由max{0,cii}取代C的对角元素cii(i=1,2,…,n)所得到的.

2016年，Kayar等[3]在文献[2]的基础上研究了脉冲线性Hamilton系统

(5)

的Lyapunov不等式，得到了如下结果.

其中

α(t)=max{[μ(A(t))]+,[μ(-A(t))]+}, [m(t)]+:=max{m(t),0}.

本文的主要目的是运用等价代换和矩阵测度的方法把定理1和定理2推广到系统(1).因系统(1)和(5)具有不同的脉冲强迫，本文对系统(1)所推导出来的Lyapunov不等式比系统(5)的Lyapunov不等式更优(见本文定理4和注1).因此，研究系统(1)的Lyapunov不等式是有意义的.

1 预备知识

对于x∈Rn和A∈Rn×n，定义

分别是向量的Euclidean范数和矩阵的矩阵范数.我们有

|Ax|≤|A||x|,x∈Rn.

(6)

因为

(7)

对于A∈Rn×n，矩阵测度μ(A)[3]定义为

且有

(8)

其中λmax(D)表示矩阵D的最大特征值.

如果V(t,s)是

(9)

的基解矩阵，且满足V(s,s)=I，那么有

(10)

(11)

记

2 主要结果

其中

证明定义M0=I,Mk=AkAk-1…A1,k=1,2,…,m.对于每一个k=1,2,…,m，设

Mku(t)=x(t),Mkv(t)=y(t),t∈(tk,tk+1),

其中a=t0,b=tm+1.

易见上述变换把(1)转化为

(12)

设V(t,s)是(9)的基解矩阵，则有

(13)

把t=t0,ξ=a,b代入式(13)，得到

(14)

和

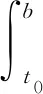
(15)

由式(10)和(14)得

(16)

对不等式(16)应用Cauchy-Schwarz不等式，有

(17)

同理，

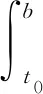
(18)

另一方面，我们容易得到

(19)

和

(20)

对式(19)从a到b积分，并利用式(20)可得

(21)

因为B*(t)≥B(t)，且当t∈[a,b]时有|v(t)|≤|v(t0)|，对式(21)有如下估计：

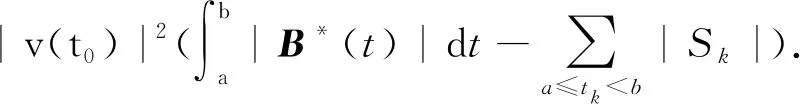
(22)

利用不等式(17)和(18)，从式(22)可得

(23)

其中

因为q1+q2=1，所以

由式(23)得

所以最终得到

注1注意到定理3得到的Lyapunov不等式左边最后的部分是两项之和，而本文得到的定理4中Lyapunov不等式左边最后的部分是两项之差，易见定理4中的Lyapunov不等式要比定理3中的Lyapunov不等式更优.

由定理4自然可得下面的推论.

其中