基于键相信号截取的整周期采样方法

张烨

（西安紫星电子科技有限公司，陕西西安，710072）

0 引言

在进行转子动平衡分析时，需要准确测量转子基频振动信号的幅值A和相位θ。对于采样序列x(1)、、x(2)、…x(N)，基频振动的幅值A和相位θ与FFT基频幅值A1和相位θ1存在关系：A= 2A1/N,θ=θ1，其中N为采样点数（满足N= 2n，n为正整数的条件），因此一般都是通过对振动信号进行FFT来计算A和θ。根据数字信号处理理论可知，对N点采样序列进行傅立叶变换后，如果序列为非整周期截断，则会因为谱泄漏造成FFT幅值和相位的失真[1]，从而不能准确得到基频振动的幅值和相位。解决这个问题的有效办法就是采用整周期采样。

常用的整周期采样方法是通过数字锁相环[2]来实现的。其基本原理是在锁相环和计数器的共同配合下，键相信号在锁相环输入端产生一个脉冲信号，输出端就会输出N个脉冲信号触发A/D转换，实现N倍频的整周期采样。由于当前采样脉冲输出频率是根据上一周期得出的，如果转速波动引起周期变化较大，那么这种方法也并不能真正实现整周期采样。此外，锁相环的时基分辨率对于采样也有较大影响[3]。因此该方法适用于转速较低、波动较小的场合。某型航空发动机转速高、速度波动较大，不适宜采用锁相环来进行整周期采样。针对这个情况，本文利用软件方法，通过键相信号作为振动信号整周期截取的依据[4]，实现了整周期采样。

所谓键相信号，是由安装在转轴上的涡流传感器在转轴每转一圈时产生的脉冲，它的每一个脉冲唯一对应于转子周向一固定点，可以用于确定转子上其它径向振动量信号的相位，该脉冲能为振动信号提供转轴每转一圈时的参考标准。由键相信号产生采样触发信号，即作为振动信号整周期采集的外触发脉冲，同时一通过两个键相信号之间的时间间隔来换算转换记录实时转速值，键相信号也可以用于确定转子上其它径向振动量信号的相位。

根据频谱分析的要求，必须对振动量进行整周期采样以避免傅立叶离散变换时的泄漏效应与栅栏效应。因此，要求振动量采样的触发脉冲频率必须能跟随机组转速的变化而相应变化。另外转速自身作为进行振动分析的一个极其重要的参数,也要求能够准确及时地获得。这些问题，都可通过对转子的键相信号进行实时处理而解决。

键相信号可以用光电式、涡流式、磁电式传感器对转子上的标志区或键槽进行检测来拾取。通常我们用涡流式传感器来检测键相信号，要得到好的信号,关键是键槽的形状、尺寸及在转子上开槽的位置以及传感器安装的位置，键槽及传感器的安装。

旋转机械振动测试中，一般是通过在旋转机械的轴上开一键槽，然后装上振动信号传感器，便可以测得原始键相信号，该键相信号是用来对旋转机械进行测速与振动信号整周期采样的基准信号。

1 依据键相信号的整周期截取

■1.1 整周期截取原理

在旋转机械动平衡时，一般都需要采用键相信号作为计算相位的参考基准。在发动机转子前端的整流罩上贴上反光贴片，光电传感器对准整流罩，当反光贴片转到光电传感器位置时，产生一个键相脉冲。两个键相脉冲之间转子必然正好旋转了一周，两个键相脉冲的时间间隔也必然为信号的周期，因此可以考虑采用键相脉冲作为信号整周期截取的依据。

采用固定采样率连续同时采集若干时间内的键相信号和振动信号（这里采集时间长度t至少应该大于1个周期以便截取数据），如图1所示，两个键相脉冲上升沿之间的时间间隔即为信号周期T，所采集的N个点也必为1个整周期的数据，从而实现了对信号的整周期截取。

图1 键相信号整周期截取原理

由于采用键相信号而不是实现设定好的固定点数作为整周期截取的依据，当周期变大时，截取数据点数会相应增多，当周期减小时，截取数据点数会相应减小，始终保证是整周期截取，从而避免了转速变化的影响。

■1.2 采样率的确定

由于需要根据两个键相信号的上升沿来确定信号的周期T和实际采样点数N，能否及时捕捉到键相信号的上升沿对于决定能否对信号实现整周期采样具有重要意义。如果键相信号捕捉不及时，则必然引起周期测量误差，从而造成非整周期截断。

设信号周期为T，在该周期内的采样点数为N，采样间隔时间，则通过采集两个键相脉冲测出的周期误差将不大于，相对误差为。本文对信号在不同的整周期截断相对误差条件下进行了仿真分析，结果如表1所示。从表2中可以看出当每周期只采集10个点时，幅度误差达到0.169，相位误差更是接近了18°，而当每周期采集200个点时，幅度误差仅为0.0001，相位误差也不超过1°。可见每周期采样点数越多，周期测量越准确，越接近于整周期截断，幅值和相位误差也越小。

综合考虑周期的波动和每周期所需的最小采样点数，则系统的采样率应该要满足：

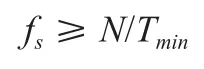
其中Tmin为转子的最小周期。

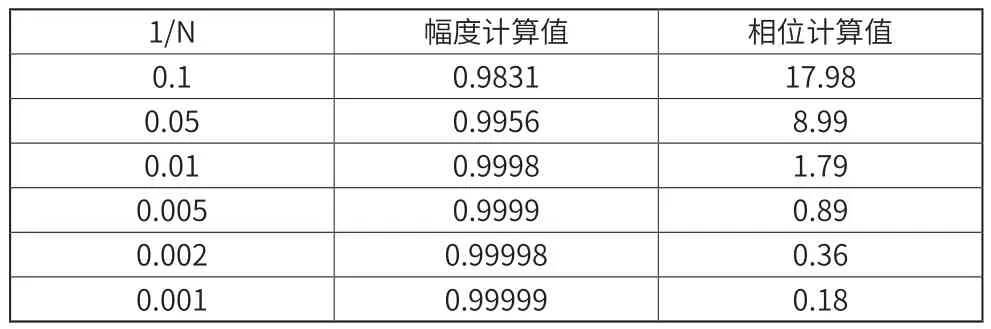
表2 采样点数对分析结果的影响

■1.3 反光贴片的影响

为了保证每个周期内都能捕捉到键相信号，还必须满足采样时间间隔必须Δt小于键相脉冲宽度τ，即T/N＜τ。设反光贴片宽度为w,转子半径为r，又有τ/T=w/(2πr)，则结合两式可以推得w>2πr/N。反光贴片宽度w和转子半径r以及采样点数N必须要满足w>2πr/N的条件才能保证键相信号的采集。

2 键相信号误差分析

键相信号的误差分为频率误差和相位误差。

■2.1 频率误差

因时钟源采用石英晶体振荡器，时钟频率f误差极小，可认为是0。周期误差就是两个键相脉冲的时间间隔t和计数器N所代表时间之间的差值。

假定任一时钟脉冲为时间原点，并把其后的脉冲按顺序标记为1,2,3…,两个相邻的键信号到来的时间分别为t1和t2，紧随其后的时钟脉冲分别为n1和n2。

可知：n1=[t1×f]+1；n2=[t2×f]+1

f：时针分期后f：时针分期后f：时针分期后f：时针分期后f：时针分期后频率f=f∅/64

[]表示取整函数，这样键信号周期的绝对误差：

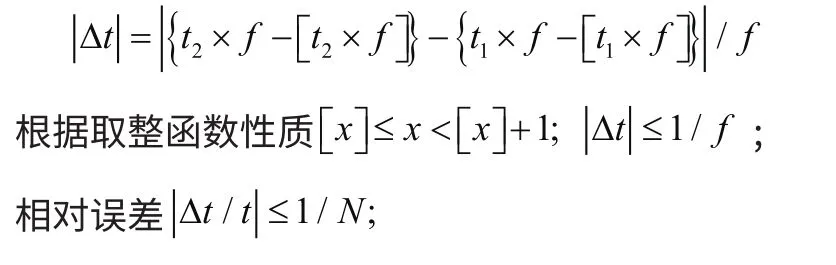
N:计算器的计数值

尤其可得出两个结论：（1）提高时钟频率可减小误差；（2）当转子转速越高测量误差越小。

■2.2 相位误差

针对传感器对轴的径向位移进行整周期采样，要求采样点在轴上均匀，且每一次采样的位置固定。这样才能从采样数据中分离出正确的相位信息。一般用产生键相位的槽作为起点，其他的点均分布在轴上。但是由于安装等各种原因，并不能做到每次采样的位置固定。采样点与这些固定点的偏差即为相位误差。

相位可分为初始误差和累计误差两部分。相位初始误差为第一个采样脉冲和键相信号之间的相位差，相位积累误差是由于采样脉冲和键相信号之间的频率不一致导致的，即：

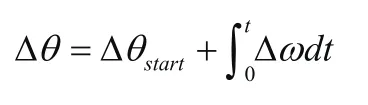
3 信号的插值重构

采用上述方法得到的采样点数N往往都不能满足N= 2n(n为正整数）的条件，不便于进行FFT变换。为此再对采集的N个数据进行插值，重构出能够直接进行FFT变换的N′个点[5]。

插值[6]的方法有多种，本文采用分段二次插值来重构信号。对于任意一个子区间（对应三个节点tk−1,tk,tk+1），均可构造一个二次插值多项式

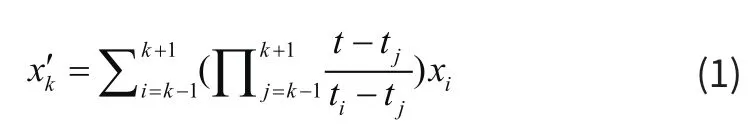
其中tk−1≤t≤tk+1。为尽可能减小插值误差，插值节点的选择应满足如下条件：

设在周期T时间内采N个信号x1,x2,x3…xN′'，其对应的采样时间分别为

t1= 0 ,t2=∆t,t3=2 ∆t, … ,tN′−1= (N− 1 )∆t， 其 中 ∆t=T/N为实际的采样间隔时间。今需要在周期T内插值重构N′个点，则重构的N′个点对应的采样时间分别为：

=其 中 ∆t′=T T/N′为 重 构 的采样间隔时间。分别以为插值点，根据（1）式即可计算出重构后的信号

4 平均处理

不平衡振动量是与转速密切相关的，因此利用不同周期内的数据计算出的振动幅度和相位可能都不同。可以将多个周期内的振动幅度和相位分别进行平均，得到平均状态下的振动幅度和相位以用于指导动平衡。此外，多周期的平均处理也有利于消除随机噪声的影响。

5 结论

（1）采用键相信号作为整周期截取的依据可以有效避免转速波动的影响，克服了锁相环触发整周期采样的缺点。

（2）采样率对于计算结果具有重要影响。采样率越高，越接近于整周期采样。此外提高采样率也有利于减小信号插值重构的误差。

（3）对多个周期内的幅值和相位进行平均处理以减小随机干扰。

键相信号作为输入提供给分析诊断系统用于描述转子的相位，还可提供给偏心测量模块键相信号，用于偏心值的计算，该信号是偏心值计算所必需的。因此键相信号的测量在机组保护监测系统中起着相当重要的作用。

实际转子振动除了基频分量以外，还可能有多次谐波和次谐波分量。对于以不平衡故障为主的转子振动而言，其基频分量占优，谐波分量很小，对整周期截取后谱泄漏的影响很小。当转子存在其它故障时，谐波分量特别是非整数倍谐波分量较大时，按基频信号进行整周期截取后，谐波分量并未能被整周期截取，仍然会造成谱泄漏，影响到基频信号的幅值和相位。因此若存在较大的谐波分量时，可以考虑将其滤掉，以免影响基频信号的分析结果。