结构参数对地铁引起建筑结构噪声影响分析

刘长卿

（上海市环境科学研究院 上海城市环境噪声控制工程技术研究中心，上海 200233）

城市轨道交通以其快速、便捷、节能等优势在大型城市交通网中的作用越来越突出。伴随着城市轨道交通的大力发展，其运行引起的环境振动及二次结构噪声扰民问题也来越受到人们的关注。对于上海、北京、广州等特大城市，地铁下穿居民区的情况十分普遍，地铁引起的振动可直接传递至建筑内引发楼板振动，同时，振动引起的二次结构噪声也给人们的生活带来影响。近年来，国内外研究人员针对地铁引起的振动及结构噪声问题做了大量研究工作。辜小安等[1]对我国城市轨道交通列车运行引起的建筑物二次辐射噪声的预测和参考标准的适宜性进行了探讨。Zou等[2]针对地铁车辆段不同位置引起的建筑振动和二次结构噪声进行了测试分析，对新建地铁车辆段的规划设计提出了建议。邬玉斌等[3]以地铁邻近音乐排练厅为例，对建筑室内振动和二次结构噪声进行了实测与数值仿真，得到了地铁引起的建筑室内结构噪声影响规律并验证了数值计算的可靠性。陈俊杰[4]提出了地铁列车振动影响下建筑结构二次辐射噪声预测方法，并选取北京某邻近地铁建筑进行结构噪声实测，对该预测方法进行了验证。Mouzakis等[5]利用实测传递函数法对地铁引起的住宅建筑内振动及结构噪声进行了评估，并提出了控制建议。杨尚福[6]通过仿真计算研究了软土层、硬土层和硬质岩层3种土体条件下地铁引起的建筑振动及结构噪声影响。张宇明等[7]以某营运中的地下双层地铁停车场为研究对象，通过实测法及数值分析法研究了地铁上盖建筑地铁振动及二次结构噪声影响。我国国家环保部发布的2008版和2018版的《环境影响评价技术导则城市轨道交通》（HJ 453）中均给出了轨道交通引起的建筑结构噪声预测公式。

以往研究成果以结构噪声的预测方法研究为主，未涉及到对影响结构噪声的结构材料参数分析。本文基于以往的研究方法及成果，选取上海某地铁线路及其上盖邻近建筑为研究对象，采用半实测半数值的振动分析方法以及经验公式法计算地铁引起的邻近建筑室内结构噪声，分析建筑结构噪声对混凝土和土层弹性模量、阻尼系数等参数的敏感性，为城市轨道交通引起的建筑室内二次结构噪声降噪设计提供参考。

1 结构噪声计算方法概述

针对地铁引起的建筑室内结构噪声问题，首先采用半实测半数值的振动分析方法，计算得到建筑室内结构的振动响应，即建筑室内楼板垂向振动加速度级（计算方法详见文献[8-9]），然后根据楼板振动预测结果，利用理论公式法，对结构噪声进行预测。

基于Kurzweil模型[10]，被振动激励的建筑物表面辐射的声功率为

式中：W为建筑结构振动激发的声功率，Z0=ρ0c0为空气特性阻抗，σ为声辐射效率。S为室内地板的面积，v为地板表面振动速度。

考虑了直达声和混响声两部分，室内声压可表示为

式中：r是地面到测量点的距离，R为房间常数，与房间内平均吸声系数和房间总表面积有关。

房间内结构辐射声的声压级Lp可表示为

将式（2）代入式（3），得到：

式中：Lv为振动速度级，C为常数，表达式为

地铁振动近似假设为简谐振动，则单频结构噪声声压级Lp,f可表示为振动加速度级的函数：

Ca为常数，表达式为

式中：VLf为振动加速度级频率响应，ω为简谐振动圆频率。

综上，当房间常数R及房间尺寸参数确定时可得到Ca值，在利用半实测半数值的振动分析方法得到室内楼板各频率振动加速度级VLf的情况下，通过式（6）即可求出各频率对应的结构噪声声压级Lp,f。

2 数值模型及结构材料参数设定

本文选取的待分析建筑为地铁邻近上盖住宅建筑，其中地上部分共13层，高度约40 m，地下部分为2层的车库和设备间，深度约10 m。地铁线路从建筑侧下方穿过，其站台上方紧邻住宅地下室，地铁位于地下5层，埋深约30 m。地铁线路与建筑相对位置示意图如图1所示。

图1 地铁线路与建筑位置示意图

根据该建筑与地铁工程设计图，建立三维有限元模型。为减小土层边界反射波影响，模型边界采用黏弹性人工边界。激振力载荷施加在站台轨道道床处，沿行车线施加多点激励单位载荷，计算靠近地铁站台一侧L01～L13楼层房间的结构噪声（结构模型如图2）。

图2 三维有限元结构模型

钢筋混凝土结构材料参数按实际结构设计的混凝土等级设定，如表1所示。土层类型根据该地块地质勘查报告及《建筑抗震设计规范》（GB50011－2010）[11]进行简化，等效参数见表2，其中ρ为土层密度，μ为泊松比，E为动弹性模量。上述材料参数在计算中均作为设计值输入模型。

表1 混凝土等效参数

表2 土层等效参数

3 振动源强

地铁运行过程中，列车与轮轨间的相互作用引起道床振动，并经由隧道结构传递到土层以及邻近建筑中。轨道道床作为振动的源头，其振动特性及振动强度对于环境振动的预测至关重要。由于待分析地铁线路已开通运行，为了准确获取振动源强，对待分析地铁线路进行了道床振动源强测试。道床测试点位照片如图3所示。测试过程中，采用IEPE型加速度传感器KD1050L以及德国HEIM DATaRec 4 Series 24通道数据采集仪连续采集10组列车经过时的道床垂向振动加速度数据，列车车型为A型车。

图3 道床振动源强测点照片

由于篇幅限制，仅展示某一次列车经过时的道床振动加速度时程曲线，如图4所示。将10组列车经过时道床铅垂向振动加速度进行平均处理，得到加速度级1/3倍频程频谱如图5所示。利用该源强频谱结合有限元模型可计算建筑楼板铅垂向振动加速度级。

图4 某列车经过时道床铅垂向振动加速度时程曲线

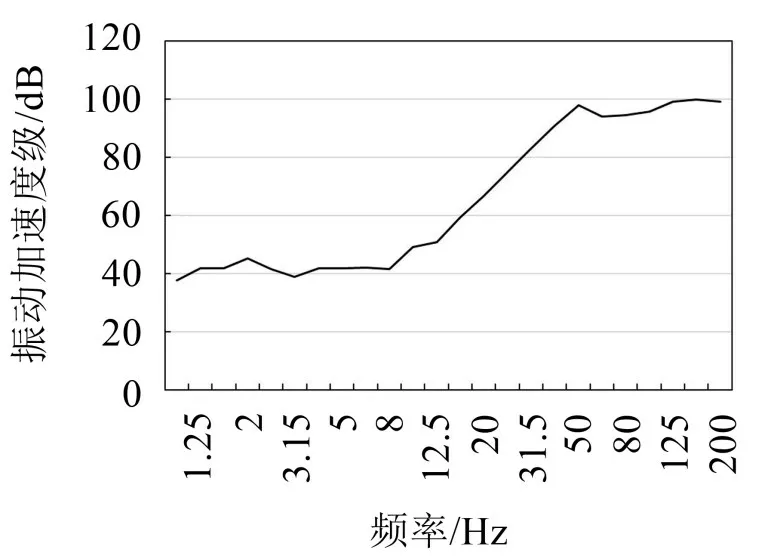
图5 道床振动源强加速度级频谱10列车平均值

4 室内振动及结构噪声分析

4.1 各楼层振动及结构噪声计算结果

根据实测振动源强频谱，利用半实测半数值的振动分析方法，可求解建筑室内楼板垂向振动加速度级。根据《城市轨道交通引起建筑物振动与二次辐射噪声限值及其测量方法标准》[12]，地铁引起的建筑结构二次辐射噪声主要频段为16 Hz～200 Hz，故本文对楼板振动仅计算16 Hz～200 Hz频段内振动加速度级，对结构噪声仅计算16 Hz～200 Hz频段内总的A计权声压级。

对本文待分析房间结构噪声的预测，取空气密度ρ0=1.29 kg/m3，声速c0=340 m/s，声辐射效率σ≈1，室内地板的面积S=10 m2，房间高度为2.8 m，混响时间为0.8 s的一般装修房间常数R=5.64，代入式（7）可求得地面上r=1.2 m处的Ca值为35.7，将半实测半数值法求解的建筑室内楼板不同频率的铅垂向振动加速度级代入结构噪声预测公式（6），可计算得到不同频率的室内结构噪声值Lp,f，利用A计权网络对其1/3倍频带中心频率声压级计权后进行能量叠加，可求出待分析频段内总的A计权声压级。

各楼层靠近地铁一侧的房间楼板垂向振动及结构噪声预测结果如图6至图7所示。结果表明：

图6 楼板振动及结构噪声随楼层变化对比曲线

图7 部分楼层结构噪声频谱对比

（1）结构噪声A声级随楼层升高整体呈减小趋势，但部分楼层有回弹放大现象；

（2）楼板垂向振动与结构噪声呈现正相关，两者随楼层升高变化趋势一致；

（3）结构噪声影响较大的1、4、13楼房间结构噪声1/3倍频程频谱曲线对比可见，随着楼层升高，40 Hz以上较高频段结构噪声迅速衰减，40 Hz以下较低频段噪声略有放大。

4.2 结构参数对室内结构噪声影响分析

分别将结构模型中混凝土和土层的弹性模量E和阻尼系数ξ按表1、表2原始设计值±20%浮动取值计算室内结构噪声，并与原始设计值对应的结构噪声计算结果对比，分析上述参数对室内结构噪声的影响。

各楼层靠近地铁一侧的房间结构噪声对材料参数敏感性分析结果如图8至图11所示。结果表明：

图8 混凝土弹性模量对结构噪声影响

（1）结构噪声对混凝土弹性模量敏感性最强。在混凝土弹性模量设计值±20%浮动条件下，结构噪声对混凝土的弹性模量敏感性最强，建筑室内A声级出现最大8.2 dB的波动，变化比例最大为38.9%；

图9 混凝土阻尼系数对结构噪声影响

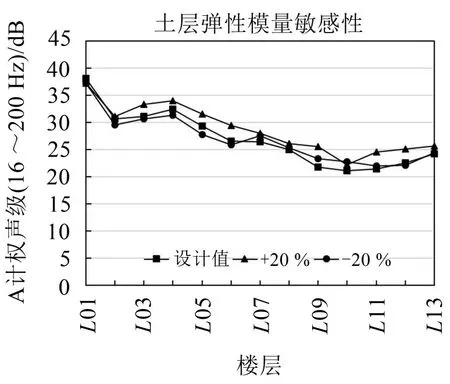
图10 土弹性模量对结构噪声影响

图11 土阻尼系数对结构噪声影响

（2）结构噪声对土层弹性模量敏感性次于混凝土弹性模量，在土层弹性模量设计值±20%浮动条件下，室内A声级最大3.8 dB的波动，变化比例最大为17%；

（3）结构噪声对混凝土阻尼系数敏感性较低，在混凝土阻尼系数设计值±20%浮动条件下，室内A声级最大波动1.7 dB，变化比例最大为6.3%；

（4）结构噪声对混凝土阻尼系数敏感性最低，在土层阻尼系数设计值±20%浮动条件下，室内A声级最大波动0.8 dB，变化比例最大为3.9%。

5 结语

本文利用半实测半数值的振动分析法和经验公式法对地铁引起的建筑室内二次结构噪声进行了计算，分析了混凝土和土层弹性模量、阻尼系数等参数在原始设计值基础上±20%变化幅度的情况下对建筑室内结构噪声的影响，得出以下结论：

（1）结构噪声A声级随楼层升高整体呈减小趋势，但部分楼层有回弹放大现象。楼板垂向振动与结构噪声随楼层升高变化趋势一致。随着楼层升高，40 Hz以上较高频段结构噪声迅速衰减，40 Hz以下较低频段噪声略有放大；

（2）在单项参数±20%浮动条件下，结构噪声对混凝土的弹性模量敏感性最强，建筑室内A声级出现最大8.2 dB的波动，变化比例最大为38.9%；对土层弹性模量敏感性次之，A声级最大3.8 dB的波动，变化比例最大为17%；对混凝土和土层的阻尼系数敏感性均较低，A声级最大波动不超过2 dB，A声级变化均在7%以内；

（3）地铁邻近建筑减振降噪设计中，由于混凝土弹性模量对结构噪声影响最大，在保证结构安全性的前提下，应选定合理的混凝土强度等级，以确保其弹性模量有利于降低室内结构噪声的影响。