变流器穿墙套管安装板在随机载荷下的振动疲劳寿命分析

张强强，史江，刘莉

（1.中车永济电机有限公司，山西 永济 044500；2.西安交通大学 机械结构强度与振动国家重点实验室，西安 710049）

近几年来，我国高速铁路快速发展，动车组运行速度在不断提高，车辆的服役环境也愈发恶劣，给列车各个部件的结构强度带来了更严峻的考验。轨道不平整、气流扰动以及外部环境等因素，都会使动车组列车运行中产生振动[1]。变流器穿墙套管安装板是位于直接安装于车体上部的柜体变流器中，其下部连接着重要的铜排电路，若不能保证安装板在冲击和振动等随机载荷作用下的疲劳性能，则会导致结构内安装的电气元器件无法正常工作，甚至危及列车行驶安全，因此必须对穿墙套管安装板进行疲劳研究[2]。

动车组列车在实际的运行过程中有特殊的规律，承受纵向、横向和垂向的激励载荷，故会引发一定的环境振动。这些振动无法用确定的函数表示却又有一定的统计规律，车辆系统便是处于这种随机振动状态中。随机振动现象在自然界和工程中广泛存在，是导致很多设备故障和结构失效的主要原因，对于许多承受动载荷的工程结构，确保其动力学性能良好至关重要。设计者需要在结构的设计阶段，对所设计的结构在运行工况下的动力学性能进行精确分析预测。结构的动力学性能可通过结构随机振动分析来获得，而随机振动应力和应变响应不能用确定性的时间或空间坐标函数描述，所以只能用概率或统计的方法描述。根据随机过程理论，结构的随机振动响应可以在频域内用功率谱密度函数来描述，所以结构危险点位置的疲劳累积损伤和疲劳寿命可以利用功率谱密度求得[3]。

1 疲劳理论

1.1 Miner线性疲劳损伤累计理论

金属的疲劳破坏不同于其静强度破坏，在交变载荷的循环作用下，疲劳破坏可能在未达到其强度极限的应力强度下发生，并且具有隐蔽性和突发性，所以在结构设计时，必须对疲劳破坏给予关注和考虑。不同的疲劳假设和累计理论，对应着不同的计算模型，Miner理论[4]将疲劳损伤D定义为使用应力下的循环次数n与该应力下材料疲劳寿命N的比：

认为在多级不同应力幅值作用下,疲劳破坏发生时有：

式中：ni为第i阶应力水平下的循环次数。

Ni为第i阶应力水平下的疲劳寿命。

该理论同时假定：

（1）任一给定的应力水平下，每一次循环产生等量的损伤；

（2）累积损伤速度与以前的载荷历程无关；

（3）加载顺序的变化不影响耐疲劳寿命。

图1为两级载荷作用下线性累积损伤规律示意图。横坐标为第一级应力循环比，纵坐标为第二级应力循环比。

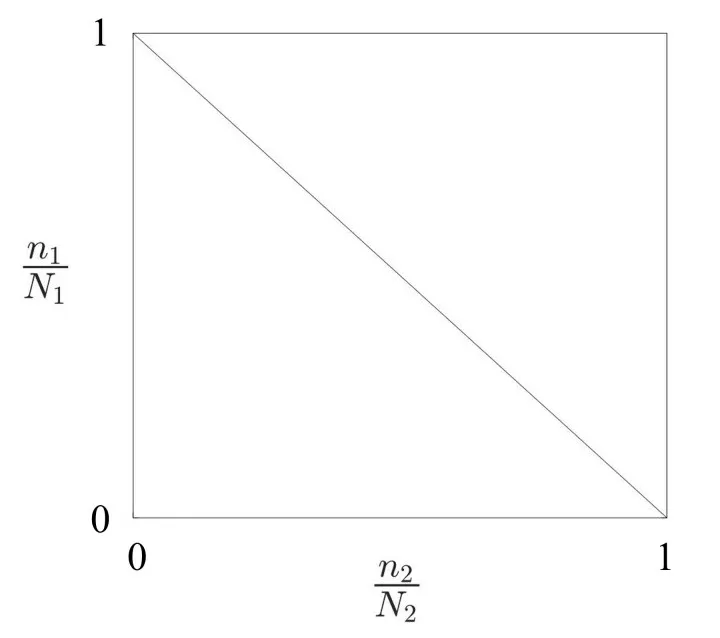
图1 线性累积损伤规律示意图

通过分析可以看出，Miner理论显著简化了疲劳机理，并且由于其表述简洁，便于理解，可抓住问题本质，所以在工程领域广泛应用。

1.2 频域疲劳分析

传统上一般是根据时域载荷信号进行疲劳寿命计算，但在有限元方法中，进行长时间的时域加载信号的处理是十分耗时，所以对于随机载荷的疲劳寿命计算，采用频域疲劳计算方法[5]。频域疲劳分析流程如图2所示。

图2 疲劳分析流程示意图

在ANSYSnCode软件中提供四种方法来评估随机振动载荷的寿命，Narrow Band，Dirlik，Lalanne和Steinberg方法[6]。Lalanne方法是一种通用宽带频载荷处理技术，本文所研究的穿墙套管安装板的工况环境极为恶劣，同时存在着低频和高频的振动环境，故本文采用Lalanne方法。

Lalanne方法应用的公式为[7]

式中：N(S)为在循环应力S下的每秒循环次数；

E(P)为期望的峰值次数；

p(S)为应力范围概率密度函数[8]。

p(S)定义为

2 模态试验测试

模态试验测试分析通常包括以下4个步骤：对结构进行激振、测量力和响应数据、估算传递函数、识别模态参数[9]。本测试采用力锤激振，通过力锤敲击试验件产生脉冲激励，同时加速度传感器测量试验件的响应，经过谱分析得到激励的自功率谱密度和激励与响应的互功率谱密度，由下式计算出频响函数，再由频域直接参数识别方法分析频响函数，得到模态参数。

式中：Gxf(ω)为激励的自功率谱密度；

Gff(ω)为激励与响应的互功率谱密度。

锤击的脉冲激励模态测试系统的基本结构如图3所示。力锤连接在PCB482C05适调仪上，对安装板进行锤击激励。激励信号和由PCB加速度传感器采集的响应信号，通过适调仪传输给比利时LMS公司的多通道数据采集、处理和模态分析系统，并最终在计算机上得到处理和分析。美国PCB公司的集成一体化的压电式（ICP®）加速度和力锤，通过PCB的传感器信号适调仪与LMS系统连接。

图3 脉冲激励模态测试测试系统

变流器穿墙套管安装板及其套管板工装激励分析图可用来说明安装板及其套管板工装的模态特性测试的基本步骤：

（1）在安装板及其套管板工装上选择一系列激振点。同时，传感器的安装位置的总原则是：能反映出被测结构的振动特性，满足测试要求。

（2）在LMS模态分析系统中，标识出测试所使用的总体坐标系，依次建立与激励点相对应的穿墙套管安装板及其套管板工装的几何点、线和面模型。同时，将模型中的各点依次和传感器及激励位置进行相互对应。

（3）确定并装夹穿墙套管安装板及其套管板工装的工况条件，将加速度传感器安装在步骤（1）中布置的某一个点上，然后在步骤（1）中设置的所有激励点依次完成敲击激励和测量。加速度传感器应避免安装在结构振动的节点或节线上，并尽可能地安装在结构响应信号较大的位置，以提高信噪比。

（4）利用LMS模态分析系统，对测量数据进行采集和分析处理，对于实验模态分析而言，数据采集至少包括所有测点的FRF和相干数据。运用稳态图作为参数识别的工具，通过分析从测量数据中提取模态参数（频率、阻尼和模态振型）。

穿墙套管安装板及下部所挂铜排导线如图4和图5所示。图4所示红线内即为所测安装板，黄色圆孔为开孔部位，图5红色方框内为铜排导线。

图4 穿墙套管安装板

图5 安装板铜排导线

受限于实际工作环境，测试点布置后的实验几何模型如图6所示。

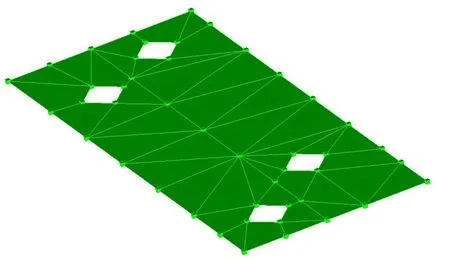
图6 安装板的实验几何模型

根据IEC61373－2010[10]轨道车辆安装设备冲击振动试验标准规定，该板只考虑150 Hz以下的振动，则所测得的主要模态参数如表1所示。

表1 安装板主要模态参数

3 有限元疲劳分析

3.1 模型建立及模态计算

（1）穿墙套管安装板等效有限元模型

安装板主体结构为一带孔的薄板，但在通孔的下部有用螺栓连接的铜排导线，铜排导线是由多片铜箔压制而成，并于底座相连接。该铜排导线并不参与分析，但需要考虑其质量和约束影响。为能够最大程度简化模型且逼近真实工况，采用Mass质量单元来进行简化代替，但实际质量不能直接使用铜排质量，需进行修正，如图7所示，圆孔中间的球形为简化的Mass质量单元。安装板通过焊接连接到变流器柜体，故需考虑四周边界条件的施加方式，通过模态试验结果与预计算结果对比发现，通过施加固定支撑边界为最合理边界。

图7 有限元模型示意图

（2）有限元模态计算

通过所建立的等效有限元模型，采用默认网格划分单元进行划分，并在孔端附近细化，设置材料为不锈钢，并对Mass质量单元修正。最终可得仿真与实测结果对比，如表2所示。

表2 仿真与实测结果对比

仿真与实验前3阶模态振型图如图8(a)至图8(c)。可以清楚地看到仿真结果可以很好的符合实验结果，同时验证了有限元模型建立的合理性。

图8 前3阶振型对比图

3.2 疲劳计算

在对该安装板进行振动疲劳仿真分析前，首先应对其有限元模型进行谐响应分析，获得用于振动疲劳分析的频率响应函数，本文选择模态叠加法进行谐响应分析的计算。基于目前铁路行业通用的IEC61373－2010轨道车辆安装设备冲击振动试验标准，根据设备在车辆上的安装位置，标准的试验值分为车体安装、转向架安装和车轴安装，而变流器属于1类A级车体安装部件，图9为1类A级设备的功率谱密度（ASD）曲线，根据上述标准，图9中x取0.532，f2取150。阻尼比在疲劳计算中也起着很大的作用，不合适的选取，会带来较大误差乃至错误的结果，但本文在疲劳计算前已对安装板进行过试验模态分析，通过表1可以看出，安装板阻尼比在1%附近，所以选取1%为阻尼比即合理。

图9 1类A级设备ASD频谱

将所有计算和选取好的参数（频响函数、ASD频谱、阻尼比、N-S曲线和Lalanne方法）输入nCode疲劳计算软件，可得如图10所示的疲劳寿命云图和图11所示的损伤云图，可以看出损伤主要集中于中间通孔连接处。

IEC61373－2010标准采用5小时的长寿命随机振动试验模拟列车安装设备25年，由图10可知，安装板寿命为9.152×105s，约为254 h，远大于5 h，并且由图11可知，其疲劳累积损伤最大值为1.093×10-6，远小于1，仿真分析疲劳寿命满足设计要求。

图10 疲劳寿命云图

图11 疲劳损伤云图

图12为损伤最大处的Mises应力在频域内的功率谱密度曲线，由图可知，在22.4 Hz附近有一波峰，这是因为在22.244 Hz上具有1阶的振动模态，可以看出在随机振动中，1阶模态振型占主要比重。

图12 最大损伤处的应力谱密度

4 结语

（1）本文通过试验模态测试，得到模态参数，然后建立有限元模型，保证了有限元模型的合理性，并且通过试验得到了疲劳分析重要的参数阻尼比。

（2）本文采用随机振动理论，结合ANSYS和nCode有限元分析软件对变流器穿墙套管安装板在频域随机振动下的疲劳寿命进行了仿真分析，比较准确地找到了安装板强度薄弱的区域，对于工程实际中安装板的振动分析具有一定的指导意义。

（3）穿墙套管安装板在随机载荷中主要表现形式为1阶模态振型，即安装板中间有较大的位移，并且由于开孔的存在，在中部连接下部所悬挂铜排导线时，要确保其螺栓连接或者焊接的可靠性，以防由于铜排掉落而引发的事故。

（4）相较于其他随机疲劳估算方法，基于频域特性的随机载荷下的疲劳强度方法有明显的高效性和高精度特性，具有更高的推广和研究价值。