基于振动测试的水下牵引机转向舵结构动力修改

王志斌，宁凡，刘聪，王志伟，高志鹏，赵坚

（天津城建大学 控制与机械工程学院，天津 300384）

波浪滑翔器是海洋中一种新型海洋自主移动观测平台，能对海洋进行持续观测，可实现大范围海表温度、湿度、盐度以及远距离海面海风、气压等环境参数的实时测量。波浪滑翔器主要有水面母船与水下牵引机组成，其前进动力主要依靠波浪能，其中转向舵是控制水下牵引机运行方向的主要机构[1]。

转向舵是当前控制水下牵引机的运行姿态的主要机构，转向舵受水下海浪涌动等的影响，其自身易产生振动，从而影响水下牵引机运行姿态的准确与稳定。国内外学者已对水下牵引机及转向舵进行了大量研究，Wang等[2]学者建立了波浪滑翔器的4自由度数学模型，使用势流理论和经验公式计算了流体力学参数，并进行了波浪滑翔器的运动仿真，为波浪滑翔器的设计提供了指导与参考；Zhou等[3]提出一种建立波浪滑翔器动力学模型的方法，同时进行了试验验证，且从模型中得到了最佳结构参数，为波浪滑翔器性能仿真及优化设计提供了基础；孙秀军等[4]等采用牛顿-欧拉方程建立了波浪滑翔器水翼动力学模型，同时进行了CFD仿真，并将仿真结果与试验结果进行了对比，得出两者数据总体趋势相近的结论；曹守启等[5]设计提出一种波浪滑翔器，其由水面母船、水下牵引机与柔性缆绳3部分组成，并对水下牵引机进行了水动力仿真研究，得出水下牵引机最大摆角在20°时推进效果最佳的结论；李小涛[6]通过对波浪滑翔器的推进动力量化分析，选取了波浪滑翔器的总体外形参数，使用ADAMS和MATLAB相结合的方法实现了建模与运动仿真分析；李灿[7]建立了波浪滑翔器动力学模型，分析了水面母船与水下牵引机的受力，仿真得到其在典型海况下的动力学特性，并对波浪滑翔器进行了海试试验；宋甜等[8]基于船舵测试数据采集的实际要求，将数据采集卡应用于船舵测试，且具有高准确性、实用性等特点，并在试验中得到证实；刘昕等[9]利用MSC.Patran和MSC.Nastran软件建立复合材料舵与钢质舵的模型并进行模态分析，得到两者各阶固有频率及振型，并比较了两种舵结构的模态节线图，分析了整舵弯曲、扭转及耦合振动模态；苏华昌等[10]采用振动台基础激励技术和激光测振仪非接触测量方法，对多面热模态特性进行了分析，并获得了1阶弯曲频率及扭转频率随加热时间和温度的变化规律；王永历等[11]对复合材料舵及钢质舵分别进行了振动特性试验，对比得出虽两者模态振型基本相同，但复合材料舵的对应固有频率高于钢质舵以及复合材料舵在局部壳板振动抑制方面优于钢质舵等结论。

1 转向舵试验模态分析

转向舵是水下牵引机的主要零部件，转向舵的动态特性直接影响到水下牵引机的运行姿态，进而影响着水下牵引机的安全运行，因此对转向舵进行模态分析是必不可少的。

本文以某水下牵引机的转向舵作为参考，对其进行模态分析。建立原始转向舵的三维模型，并导入至有限元分析软件中。转向舵由结构钢材料制成，设置其材料属性如表1。

将初始水下牵引机转向舵几何模型导入至有限元分析软件并进行网格划分，如图1所示。

表1 转向舵材料属性

图1 转向舵网格划分

对转向舵进行锤击法模态测试，使用高弹性海绵垫置于转向舵底部，采用单点激励单点响应的方法，使用冲击力锤在模态参考点施加激励，使用加速度传感器拾取响应信号，在转向舵上布置15个测点，选择11号测点作为激励点，测点布置如图2所示。采用随机子空间法（SSI）识别原始转向舵的试验模态参数。模态测试系统原理如图3所示，试验系统搭建如图4所示。

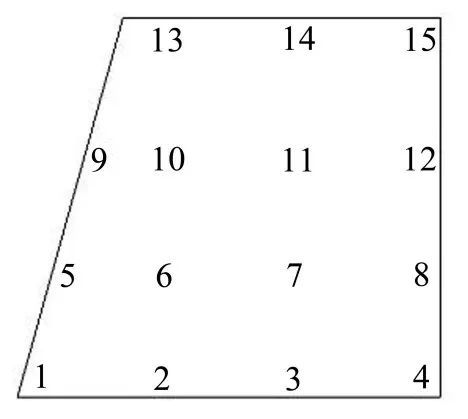
图2 转向舵测点布置图

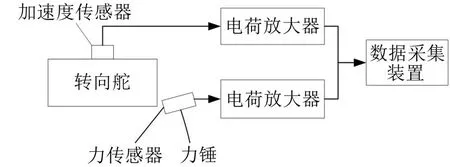
图3 试验系统原理图

图4 试验系统搭建图

采用有限元分析软件及锤击法模态测试对转向舵进行了模态分析，对转向舵进行自由模态分析，剔除刚体模态和虚假模态后选取转向舵的部分模态结果，即得到转向舵的固有频率及振型。转向舵计算模态频率和试验模态频率结果对比如表2所示，振型如图5和图6所示。

由表2中转向舵计算模态分析和试验模态分析的结果对比可知，频率最大误差发生在2阶模态处为3.3%，同时结合两者的振型结果，可以看出两种结果的模态振型具有较高的一致性，由此可以通过试验模态测试验证转向舵有限元模型的准确性。

表2 转向舵计算模态与试验模态频率对比

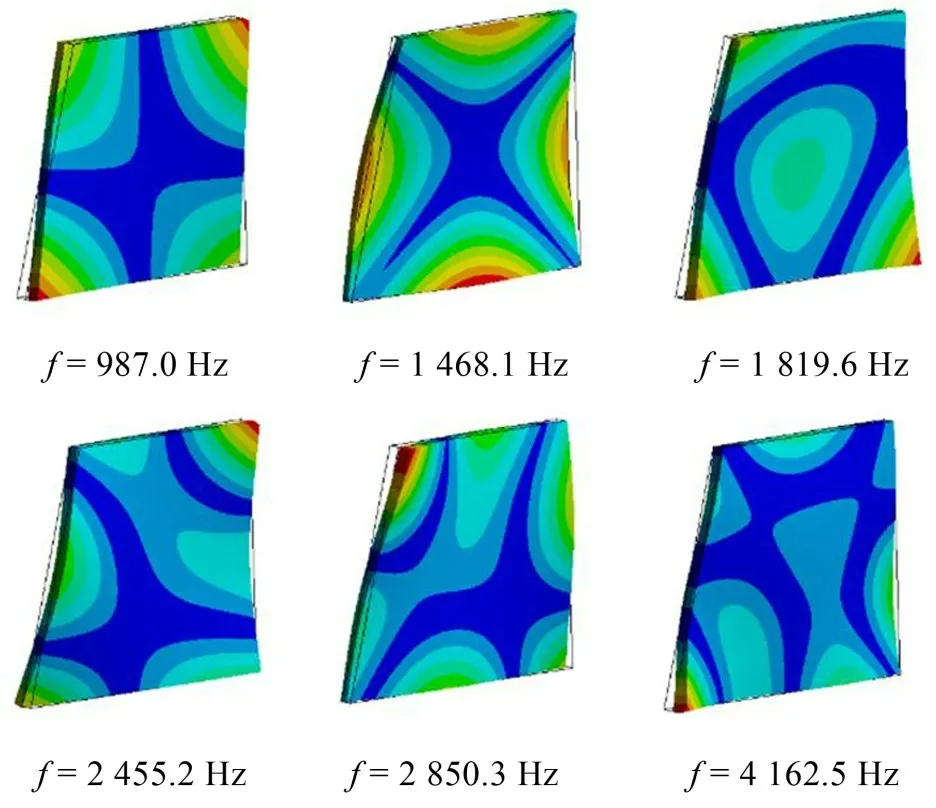
图5 转向舵计算模态振型

水下牵引机所处的海洋环境中海面状况多为轻浪，对应的海风多为和风，其中转向舵位于水下，不同于海水表面的波浪起伏，水下的海水流速极为缓慢，常见的流速为0.001 5 m/s～0.003 m/s，根据深水波公式，海浪频率为

提升抗灾能力可从农田的基本建设入手，如最大限度地发展水利、改良土壤、平整土地等。在干旱灾害多发地可以建立防护林；坚持因地制宜的原则，根据各地灾害的发生规律，推行防灾抗灾农业技术措施，在灾害来临时最大限度地减轻或避免损失。

图6 转向舵试验模态振型

其中：g为重力加速度，C为海水流速，由此可得出当前海水频率范围约为520 Hz～1 040 Hz，由此可知转向舵低阶模态频率处于海水频率范围内，极易发生共振现象，因此对水下牵引机转向舵进行结构动力修改是非常必要的。

2 转向舵结构动力修改

本文基于转向舵的模态试验结果，分析其易产生变形的原因及变形部位，提出一种水下牵引机转向舵的结构动力修改方案。修改方案在初始转向舵基础上以NACA00xx系列翼型作为参考，将初始转向舵主表面平均厚度由15 mm调整为25 mm，并根据水下牵引机的运行姿态要求，将转向舵稳流板做圆角处理，即使得水下牵引机易于破浪前进；在转向舵稳流板上方水平设计一块六边形方板，且使方板锥子头向前，使其便于调整水下牵引机运行姿态。得到修改后的新转向舵几何模型如图7所示。

图7 修改后转向舵模型

采用固定界面模态综合法[12]对修改后转向舵进行计算模态分析，其基本原理如下。

选择合适的界面，将整体结构划分为若干子结构，每个子结构作为一个超单元。将超单元的节点自由度分为边界节点自由度B集和内部节点自由度O集，从而超单元质量矩阵[Mff]和刚度矩阵[Kff]可表示为

计算超单元主模态：

式中：[Moo]和[Koo]分别表示超单元内部节点的质量矩阵和刚度矩阵；ωk和{φoo}分别表示超单元固定边界时的特征值和特征向量。

计算超单元在单元边界位移作用下的约束模态：

式中：o和b为内部节点和边界节点的自由度；φob为单位边界位移作用下的内部节点特征向量；{Ibb}为单位矩阵；{Pb}为界面结合力。

由上式可得：

式中：[Gob]为变换矩阵。

超单元在约束边界下的模态表示为

由主模态和约束模态组成超单元假设模态,也就是广义坐标变换矩阵：

用广义坐标变换矩阵同时左乘质量矩阵与右乘刚度矩阵，可分别得到缩减后的超单元广义质量矩阵[Maa]和超单元广义刚度矩阵[Kaa]：

将超单元矩阵组合至一起，得到整体结构的缩减矩阵方程，从而得到整体结构的动力学平衡方程，对整体结构进行求解。

依据模态综合法基本原理[13]，将修改后的新转向舵划分为转向舵稳流板与副板两个子结构，分别将两者导入至有限元软件中，同时设置与转向舵相同的材料属性及网格划分。子结构网格划分如图8所示。

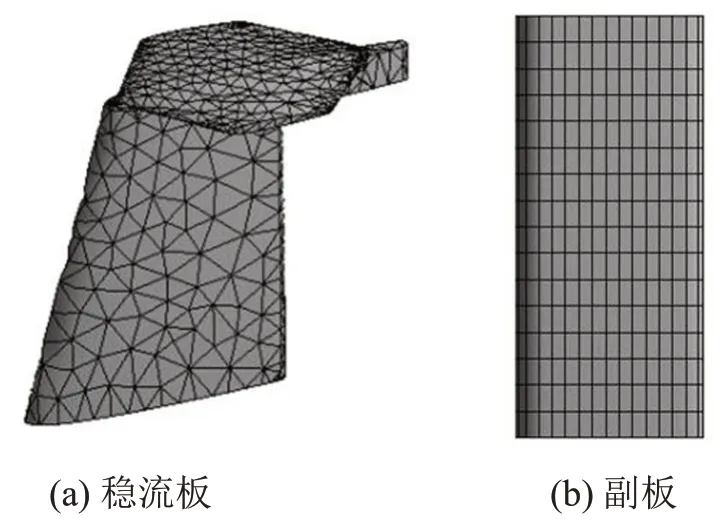
图8 子结构网格划分

对修改后转向舵的稳流板与副板进行计算模态分析，得到两者模态频率如表3所示。模态振型分别如图9及图10所示。

通过对稳流板与副板进行模态分析，得到模态参数及振型，生成超单元模型，在调用子结构超单元数据时，修改后转向舵的模态阶数小于各子结构所求模态阶数。由于子结构均为实体，在有限元软件中采用TARGE170与CONTA173接触对，生成转向舵整体三维模型，对模型进行求解。经过表2中参数指导，进行动力修改后得到的新转向舵的计算模态频率如表4所示，模态振型如图11所示。

表3 子结构模态频率

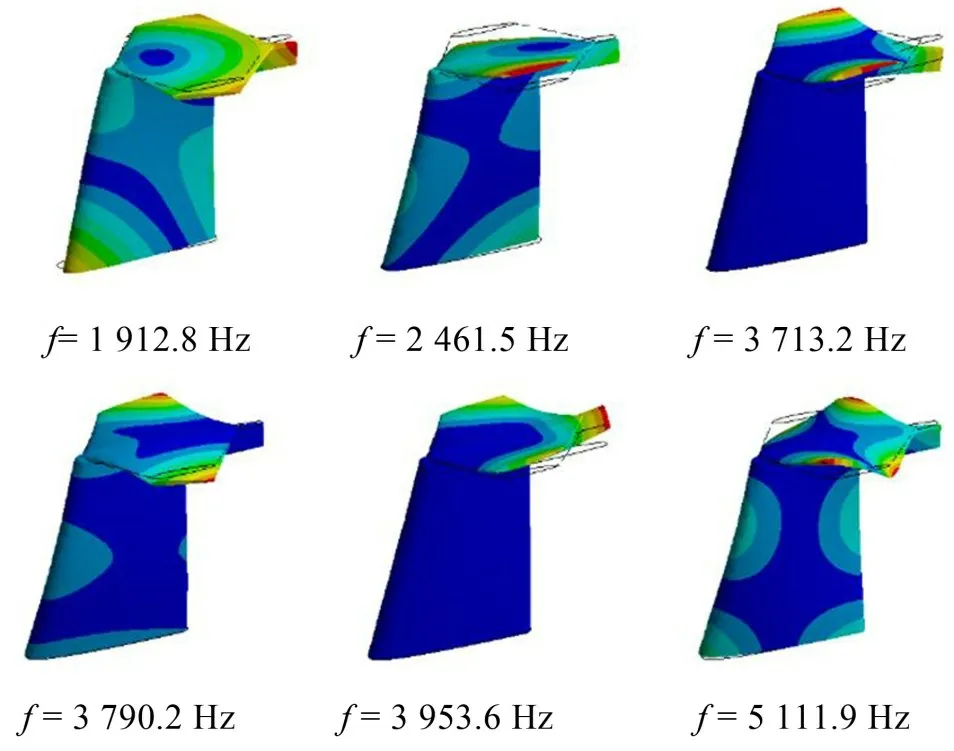
图9 稳流板振型

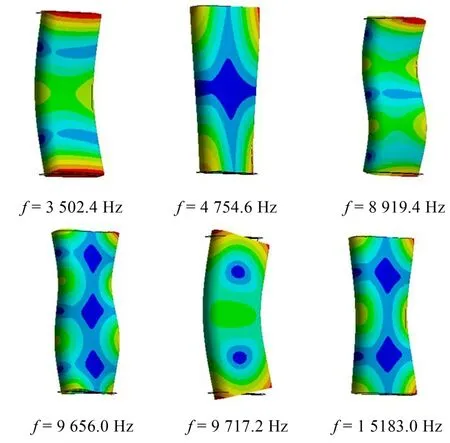
图10 副板振型

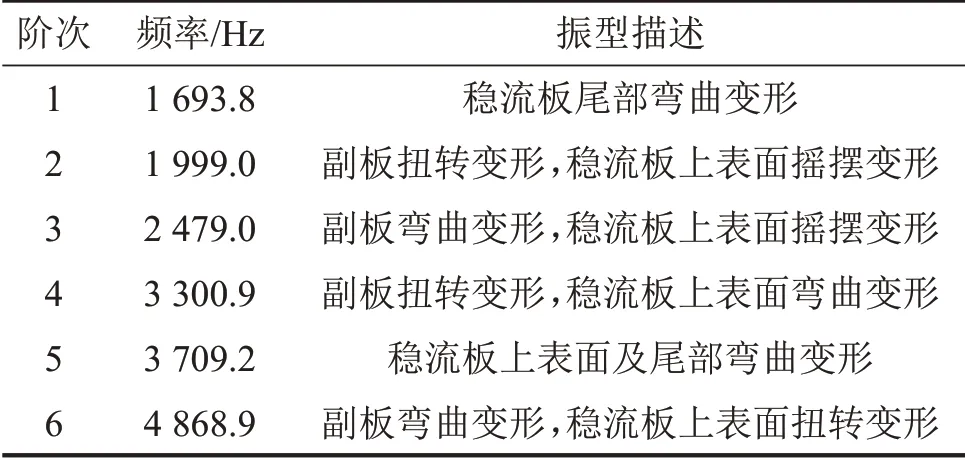
表4 修改后转向舵模态频率

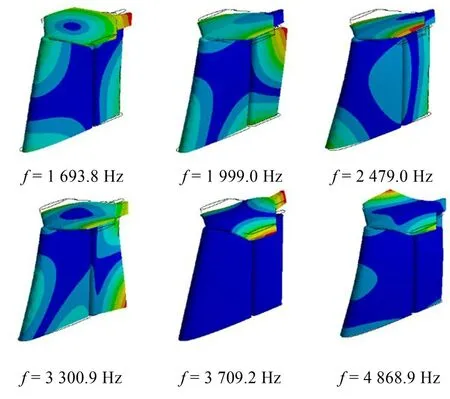
图11 修改后转向舵振型

3 结语

本文完成了某水下牵引机转向舵的锤击法模态测试，并对其进行计算模态分析，分别得到转向舵的低阶模态频率及振型，通过分析两者之间的的各阶频率，发现误差仅在3.3%以内，验证了转向舵有限元模型的准确性。

基于转向舵的计算模态和试验模态分析结果，提出转向舵稳流板添加六边形方板及将转向舵拆分为稳流板及副板的结构动力修改方案，并采用模态综合法对修改后的转向舵进行计算模态分析，修改后的转向舵各阶频率均得到不同程度提高，且避开了转向舵所在水域的频率范围，为水下牵引机转向舵的进一步结构动力修改提供了可靠数据。