一种新型Lv-cos混沌系统的弱信号检测方法研究

王伟豪，刘树勇，杨庆超

(海军工程大学 动力工程学院，武汉430033)

混沌系统对初始条件和参数具有敏感性，故可用于舰船故障弱信号检测，即系统初始条件和参数的微小变化会导致系统相轨迹发生显著变化[1-3]。目前利用混沌检测弱信号的研究用的较多的仍然是非自治的Duffing系统。王冠宇等[4]对白噪声干扰下的Duffing系统的弱信号检测进行了研究，从理论上证明了其用于弱信号检测的可行性。林红波等[5]提出了一种提取混沌噪声背景下微弱谐波信号的GRNN检测方法，验证了信噪比在-36 dB时可以检测出谐波。Li等[6]在高斯色噪声背景下检测被测信号的信噪比可达-108.45 dB。任学平等[7]通过一种改进的Duffing振子检测微弱信号系统，可检测固有频率较大的微弱信号，此系统受故障干扰时更易进入大尺度周期状态。Ma等[8]通过对Duffing振子内置频率的调整实现相同临界混沌状态下弱信号的检测。但Duffing系统在检测微弱信号时仍存在检测域度不够大的问题，当待测信号幅值超过Dufing系统本身能维持周期态的范围时系统又回到混沌状态，极大地降低了检测的范围和准确度。

三维混沌系统研究较多，但用于弱信号检测领域的系统较少，且可用的三维混沌检测系统仍些许不足。孟玲玲等[9]提出了混沌和类周期态两种状态的Lorenz检测系统。Xu等[10]利用Rosser系统与比例微分结合控制的方法检测微弱信号，增强了系统周期态的稳定性，但以上两项研究未解决收敛性与窄域性等问题。王梦蛟等[11]对陈氏混沌系统施加非共振参数激励，数值仿真得到控制参数使受控系统迅速达到稳定状态，可检测出强噪声背景下的微弱谐波信号，但是由于利用参数达到抑制状态，其稳定性和检测精度较差。刘剑鸣等[12]将周期函数嵌入典型的三维Liu混沌系统，构成了带有余弦函数的新混沌系统，该系统存在明显的由混沌到大周期态的变化，且可检测域度较宽。基于此构造原理，将谐波函数嵌入到吕系统中，获得带有余弦函数的新三维Lv-cos混沌弱信号检测系统，可检测待测信号信噪比低至-66 dB。在此基础上将变尺度系数法应用到该系统，并通过仿真实验实现仅用一组参数条件检测任意频率、任意初相位的特征信号。

1 Lv-cos混沌系统检测特性

1.1 Lv-cos混沌系统特性

2002年，吕金虎等通过混沌反控制得到混沌Lv系统，作为一种连接Chen系统和Lorenz系统的桥梁，Lv系统得到了广泛研究[13-14]。但是由于Lv系统的收敛速度较慢，限制了其混沌弱信号检测领域的的应用，本文将余弦信号嵌入到三维Lv混沌系统，得到一种新的带有余弦函数的Lv-cos系统，方程为

其中：a=35，b=3，c=28，rcos(ωt)为系统内置激励信号，利用内置激励信号幅值进行混沌系统特性分析。为简化分析，取参数ω=1，令初始条件x0=0.5,y0=0.8,z0=1，用4阶Runge-kutta法进行求解，步长取0.001 s，对稳定后的点进行特性分析，当r=30时，相空间轨迹图，时间序列图、y-z平面的庞加莱截面图和功率谱图如图1所示。利用Jcobian方法计算Lyapunov指数得λ1=0.265,λ2=-0.585,λ3=-37.26。由图1可知，相空间轨迹为混沌状态，时间序列为无序，庞加莱截面出现密集点，功率谱连续，且由最大Lyapunov指数大于0，判断当r=30时，系统(1)为混沌状态。

图1 Lv-cos系统在参数r=30的响应

1.2 Lv-cos混沌系统弱信号检测特性及数值仿真

使用Lyapunov指数可以表征混沌系统在相空间中相邻轨道间平均收敛或发散的快慢程度。当系统的Lyapunov指数为正时，平均指数率发散，系统处于混沌状态，反之为大周期状态。保持系统参数和初始条件不变，令ω=1，内置信号幅值r的变化范围为0～40 V，对Lv-cos混沌系统进行Lyapunov指数仿真和分岔图分析，结果如图2所示，由仿真结果可知：Lv-cos混沌系统在足够大范围内存在唯一临界阈值点rd，当信号幅值r＞rd时，最大李雅普诺夫指数大于0，即Lv-cos系统为混沌状态，在激励信号幅值r超过临界阈值点之前，lyapunov指数一直为负，系统相轨迹为单一周期状态，因此该Lv-cos系统能够很好地用于弱信号的检测。通过图2还可以看出此系统的大周期状态范围足够长，即对未知强度信号可检测范围足够大，因此Lv-cos系统对于同频输入信号具有广域检测性。

式(1)中，令参数r=rd，设计微弱谐波信号检测系统如下：

式中：输入信号μ(t)=d(t)+n(t)，d(t)=f·coswt,表示待检测信号或有用信号，n(t)为背景噪声。利用传统的方法难以从背景噪声中识别出待测信号，Lv-cos系统检测原理为，将检测系统调整为混沌临界状态，当输入待测信号时，系统过临界点，进入大周期态，相空间轨迹发生明显变化，未知信号被检测出来。由Lyapunov指数谱，当最大李指数过零线时，系统吸引子状态发生变化，此时的幅值r为临界值，图2(b)分岔图验证了此临界值的准确性，通过大量数值仿真分析临界值附近的相轨图最终得出较为精确的临界值为rd=26.048 49。

当输入信号μ(t)=0时，Lv-cos系统处于混沌临界状态如图3(a)所示，加入待测信号d(t)=f·cost，令f由0逐渐增大，系统开始发生变化，当f=5×10-5时，系统突变为大周期态如图3(b)所示，由图3的相轨迹变化表明系统检测到同频信号。此时加入功率P=0.01W的高斯白噪声，该条件下信噪比为SNR=≈-66 dB，系统相态仍维持在大周期态，由于噪声的干扰作用，各周期的轨迹并不完全重合，图4(a)、图4(b)分别为含噪声信号的波形图和输入含高斯白噪声信号后系统相轨迹图。

用方差为1的非高斯白噪声通过一个4阶带通滤波器产生非高斯色噪声。所设计的数字带通滤波器的传递函数为

滤波器的截止频率分别为0.3和0.4，得到非高斯色噪声如图5(a)所示，其功率为0.008 W，将其混入待检测信号中并输入Lv-cos系统中，得到输入含非高斯色噪声信号后系统轨迹图如图5(b)所示，系统相态过渡到大尺度周期态，由于有色噪声的影响，周期轨迹并不完全重合，在有色噪声背景下的信噪比为SNR=10 lg≈-65 dB。

综上所述，待测信号中含有一定量的背景噪声并不影响系统对待测信号的检测，Lv-cos混沌检测系统对不同背景噪声具有免疫性。

2 Lv-cos系统信号检测研究

2.1 待测信号频率对检测的影响

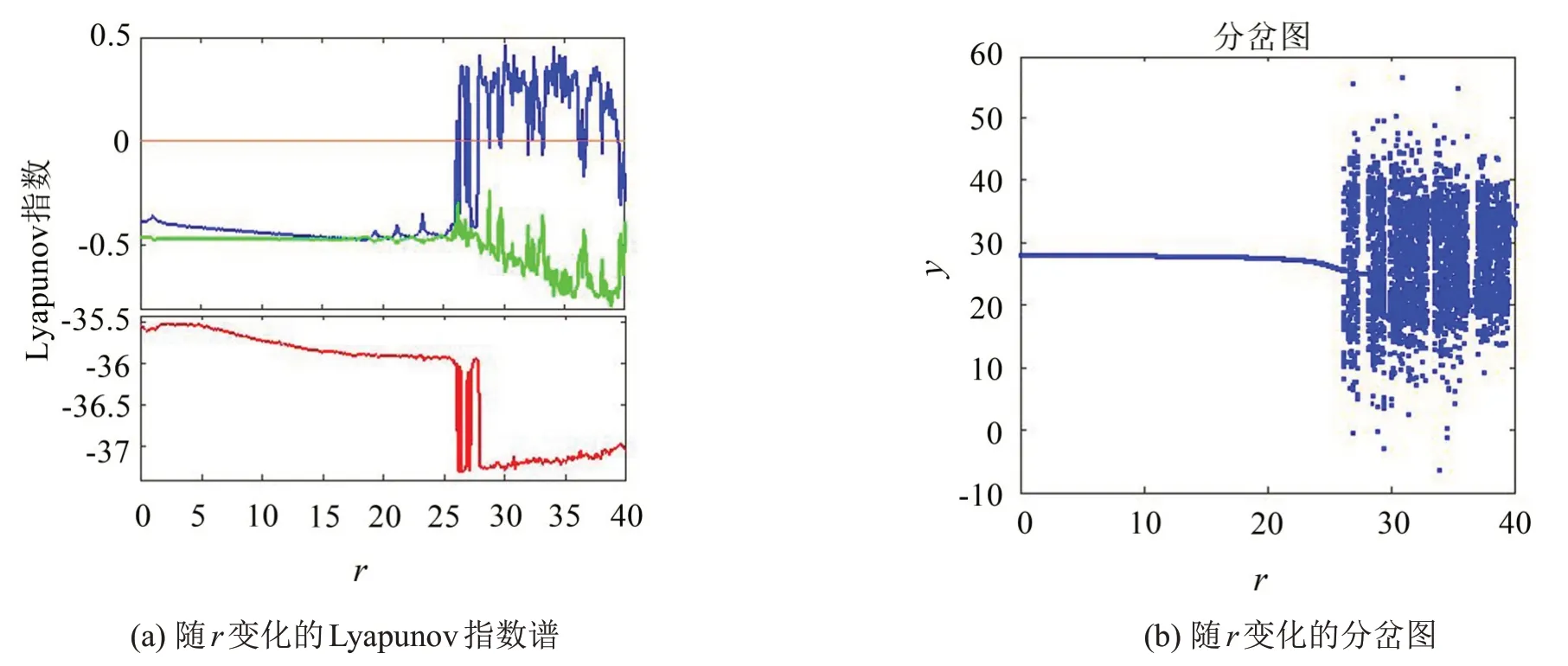
图2 Lv-cos系统的Lyapunov指数谱图和分岔图

图3 Lv-cos系统在检测弱信号时的响应图

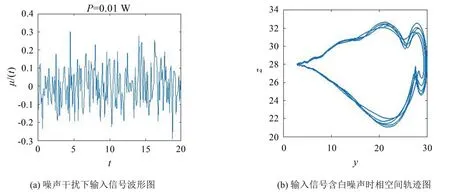
图4 输入含有白噪声信号时的系统响应

图5 输入含非高斯色噪声信号时的系统响应

以上研究是在待测信号频率与内置激励信号频率相等的情况下进行的，对于实际待测信号而言，频率往往很难确定，即使事先知道频率值，并将内置信号频率设为与它相等，也要经过大量仿真重新计算该频率参数条件下的系统临界幅值rd，如果每检测一次信号重复这个过程，显然是繁琐和不经济的。因此，采用尺度变换可很好地处理针对不同频率待测信号的检测问题[15-17]。

由变尺度思想，在不改变数值的情况下，在时间尺度上进行压缩或放大，应用于Lv-cos混沌检测系统，即将不同频率的待测信号尺度变换到已知的系统内置激励信号频率。假设待检测信号d(t1)=h·cos(ω1t1)，通过时间尺度变换令ωt=ω1t1，cosωt为原系统激励信号，得到，则d(t)=h·cosω1t1相当于待测信号频率在频率轴上压缩了倍，时间间隔增大了倍，对于三维系统表现为当三维变量对时间求导时，系数统一扩大了倍，系统由式(2)变为式(4)：

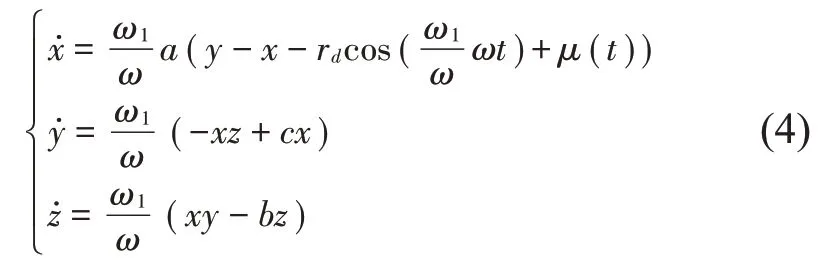
式中，仿真参数与式(2)相同，当输入信号μ(t)=d(t)=0.01cos(10t)，用式(2)和式(4)分别进行仿真研究得到图6变尺度检测结果。

图6(a)为用式(2)检测，未进行尺度变换的结果，系统状态为混沌状态，图6(b)为用式(4)检测的结果，显然通过尺度变换系统响应由混沌轨迹突变为大周期态，结论与之前的研究吻合，可以判断输入信号中含有频率ω=10 rad/s的信号成分。

2.2 待测信号初始相位对检测的影响

在上述的研究中，内置激励信号与待测信号相位等于0，而在实测工程中，待检测信号初始相位为0的可能性不大，且大小未知，因此关于待测信号相位对检测影响的研究十分有必要[18]。

在式(2)中，设待测信号初始相位为φ，内置激励信号初始相位为α，且α,φ∈[-π,π]，则信号形式可写为

通过前面分析可知，Lv-cos系统对噪声具有较好的免疫性，因此为简化分析令n(t)=0，α=0，且将待测信号频率设为ω=1，则式(5)简化为

其中：β=arctan[fsinφ/(-r+fcosφ)]。

通过上式运算，将待检测信号与系统内置激励信号合并成一个余弦函数项，β的取值只会影响相图轨迹的初始位置，对Lv-cos系统从混沌状态过渡到大尺度周期状态的阈值不会有影响。因此，只需要考虑对系统检测有影响的余弦函数的幅值，其满足下列关系式：

系统就可以从混沌变为大尺度周期状态，从而检测出微弱信号。由于待测信号相位的影响，将r取得比临界阈值rd稍大些，为相位计算留有一定裕度，取r=26.1，若已知待测信号的幅值f，则可通过式(6)求出待测信号相位φ的范围。下面以f=0.08为例进行分析说明。

取临界值rd=26.048 49，由上式可求得f=0.08时φ的取值范围是[-51.25°,51.25°]，由于φ∈[-π,π]，而f=0.08时，能检测的范围φ∈[-51.25°,51.25°]有限，其检测概率只占28.5 %，对于未能被检测出的相位可以对式子式(5)进行处理，在不改变待测信号幅值大小的情况下在幅值前加负号，即由“+”改写为“-”，则式(5)和(6)变为

通过计算，当f=0.08时，对于微弱信号能够检测出的相位范围为φ∈[-180°,-128.75°]⋃[128.75°,180°]，此时还不能对φ∈[-π,π]的检测范围达到100%，可通过引入驱动信号相位α对未能覆盖到的待测信号相位进行补偿达到检测。为方便计算，可以取内置激励信号的相位α=π/2，利用式(5)和式(7)得到如下求解相位范围的形式：

图6 尺度变换对输入信号μ(t)检测结果的影响

式中：sinφ=cos(φ-π/2)，利用式(9)和式(10)求得待测信号初始相位的检测范围分别为φ∈[38.75°,141.25°］和φ∈[-141.25°,-38.75°]。由此可知，对于幅值大于0.08的待测信号的检测，可以通过这种方式进行处理，分别令α=0和α=π/2，再各自代入方程式(5)和式(7)中得到四个方程，这4个方程可检测的相位覆盖了φ的整个区间。

以上分析是在待测信号幅值设定为f=0.08的情形下计算的，实际检测过程中，对于未知相位的检测会受到待测信号幅值的影响，当r=26.1，预估此条件下对于待测信号初始相位的检测应满足的幅值f的范围，由(6)式可得：

满足相位φ有解，得：

将rd=26.048 49代入其中，得f∈[0.05,52.15]。由此看来，以上分析设定的参数条件可检测待测信号的幅值范围满足机械故障弱信号的检测范围，可用于对待测信号初始相位的检测。

下面给出一个仿真实例，假设待测信号d(t)=0.08cos(10t+80°)，背景噪声为P=0.05 W的高斯白噪声，将待测信号与噪声信号输入到以上四个检测方程中，利用变尺度系数法求得系统的相轨迹如图7所示，(a)、(b)、(c)、(d)分别为α=0时式(5)和式(7)以及α=π/2时式(5)和式(7)进行输入信号检测的结果，只有式(5)在α=π/2时发生了由混沌向周期态转换的突变，能将ω=10 rad/s的待测信号检测出来，如图7(c)所示，其余3个检测方程均为混沌状态，不能将含有相位的待测信号检测出来。

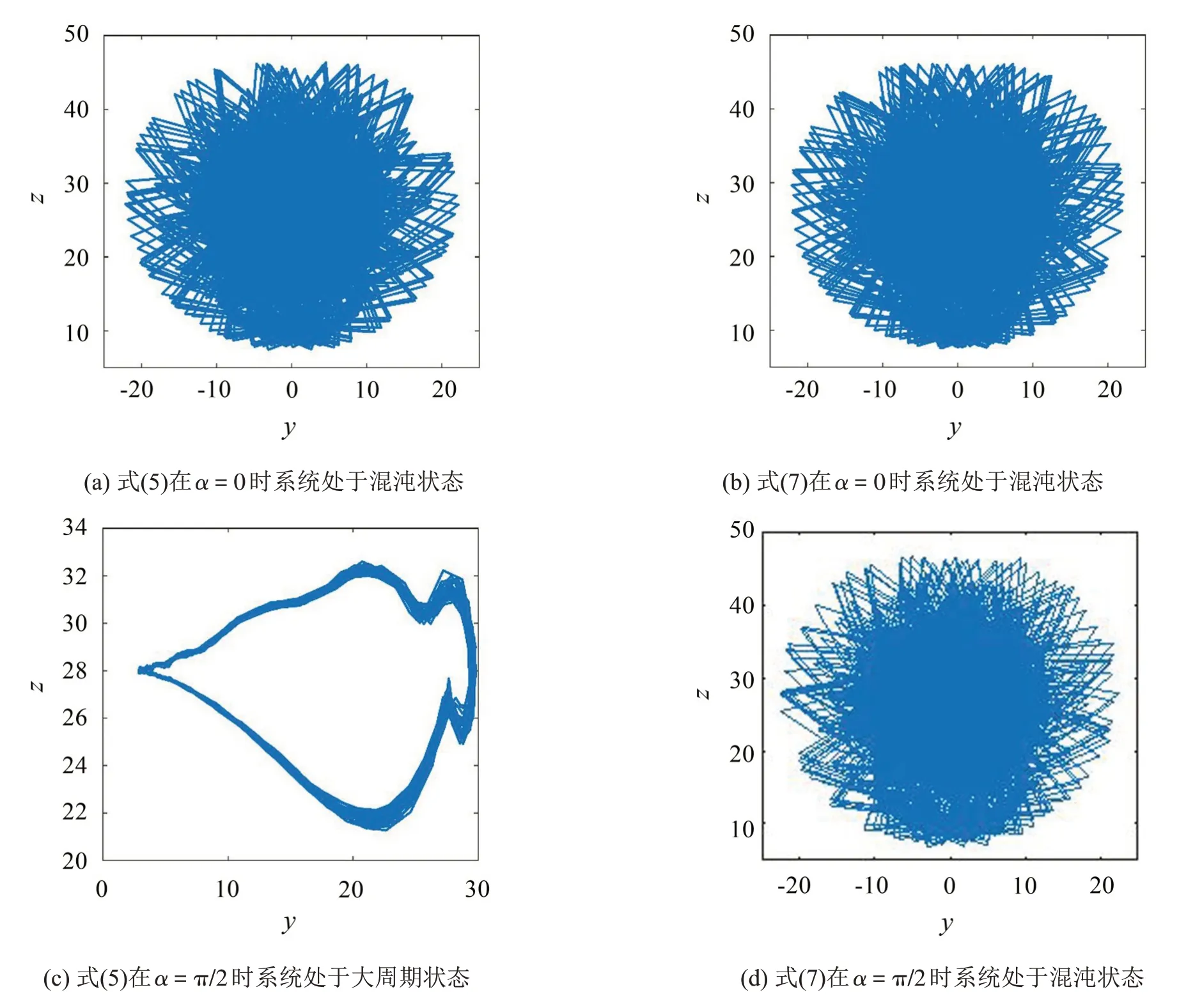
图7 待测信号相位角为80°时不同检测方程的检测效果

综上所述，当满足一定幅值条件（如h≥0.08）的待测信号中初始相位不为0时，通过考虑相位因素将方程变形为4个检测方程，通过数值分析4个检测方程的相轨变化，其中一个发生大周期突变，便可将含有频率的待测信号提取出来。

3 工程应用检测步骤

上述仿真实例表明，基于原始Lv系统构造的新Lv-cos混沌系统动力学特性丰富，对于弱信号检测是可行的，在实际工程应用时，其检测步骤为

(1)对在检测的工程信号进行初步强度估计和降噪处理，将信号强度控制在可检测范围(由系统对称性和Lyapunov指数谱可知Lv-cos系统可检测幅值范围为0.000 05～52.097)；

(2)确定系统方程参数，如初始值a=35，b=3，c=28，步长0.001 s，ω=1，r=26.1；

(3)将预处理后的待测信号输入到Lv-cos方程式(4)和式(6)中并依次取α=0和α=π/2得到4个检测方程如以上式(6)、式(8)、式(9)和式(10)4个式子；

(4)将采集的信号频率ω′通过尺度变换到与内置信号频率ω=1rad/s相同，尺度变换系数为，采用4阶Runge-Kutta法进行计算，分别求解4个检测方程得到轨迹图；

(5)通过调整尺度变化系数的值，只要有一副相轨迹图发生由混沌状态转变为大尺度周期态，即可检测到未知信号，其频率值为ω1。

4 结语

根据以上研究，可以得到如下结论：

(1)新构造的Lv-cos混沌系统能够有效地对弱信号进行检测。当系统参数处于检测阈值时，弱信号输入条件下将导致吸引子的相轨迹发生变化，由混沌变为周期；

(2)针对传统方法对待测信号大频率检测的限制，本文利用尺度变换实现了仅利用一组特定条件的参数取值完成对任意频率成分信号的检测，且操作简单；

(3)利用被测信号与内置信号进行合并后得到的幅值进行混沌到大周期状态的临界判断，解决了被测信号的相位不确定对系统检测造成的影响，可检测的相位覆盖率为100%；

(4)新构造的Lv-cos混沌系统的弱信号检测具有良好的噪声免疫性和广域检测性，在高斯白噪声背景下可检测信噪比低至-66 dB，在有色噪声背景下可检测信噪比低至-65 dB，对于强度较大的待测信号也能检测出来，这是传统Duffing振子检测系统不具备的特性，因此该系统在噪声背景下的弱信号检测有广阔的发展前景。