BTA深孔钻杆系统稳定性

马国红，杜娟

（太原科技大学 机械工程学院，太原 030024）

BTA钻杆系统是一个内部相互作用复杂的系统。钻杆的动力学行为会对加工质量产生不良的影响，例如圆度、直线度和孔表面粗糙度[1-4]。

研究人员对钻杆动力学行为的研究非常重视，开展了大量的研究。文献[5-6]建立三维动力学模型来研究深孔钻杆的固有频率。文献[7-8]为了研究钻杆系统的非线性动力学响应，构建钻杆的动力学模型，该模型考虑了切削力波动和质量偏心的影响。此外，还提出一种修正的打靶法，得到钻杆运动的周期性轨迹，并分析了钻杆系统的非线性动力学行为。文献[9]建立两种不同的动力学模型：Timoshenko梁模型和Euler-Bernoulli梁模型，分析旋转钻杆的固有频率，考虑了流体流动和轴向力的作用。文献[10]提出了一种研究颤振的模型，考虑了钻杆的支撑位置，例如在输油器、辅助支撑和基座等位置，研究了钻杆的动态稳定性。文献[11]在工件和钻杆之间，以内力的形式引入系统激励来研究深孔钻杆的涡动。

在本文中，BTA钻杆系统被视为瑞利梁模型，该模型考虑内部流体、扭矩、轴向力和支撑约束的影响。基于流固耦合和转子动力学理论，建立钻杆横向振动动力学方程，考虑流固耦合效应、转动惯量、运动约束效应、陀螺效应以及由周围流体引起的摩擦阻尼，研究了钻削深度对系统固有频率和稳定性的影响。

1 系统运动方程

在深孔加工过程中，刀具边旋转边轴向进给，而工件始终保持静止状态。图1所示为深孔钻削原理示意图，刀具以转动角速度ω进行旋转，并且其内部流动着流速为U的切削液，同时，还承受着扭矩、轴向力和支撑约束的作用。将刀具等效为瑞利梁，其中刀具的尾部视为固定端，刀具的刀头部位视为简支端。

图1 深孔钻削原理示意图

构建钻杆系统横向振动动力学模型，该模型考虑扭矩、轴向力、支撑约束、转动惯量、流固耦合、因转动引起的涡动效应和由周围切削液产生的摩擦阻尼等因素。基于转子动力学和流固耦合理论，钻杆系统横向振动控制方程：

式中：ρp和ρf分别为钻杆和切削液的密度；di和de分别为钻杆的内径和外径；Ap=π()/4为钻杆的横截面面积；Ip=π()/64为钻杆的横截面惯性矩；Af=4为钻杆内孔的横截面面积；If=/64为钻杆的横截面惯性矩；P为钻头所承受的轴向力；T为对钻头所承受的扭矩；Ka,Ca和Kb,Cb分别为位于xa和xb处的支撑刚度和阻尼系数；wx和wy分别为沿x和y方向的横向振动位移。

令w=wx+iwy,且i=并将式(1)和式(2)进行合并，得到：

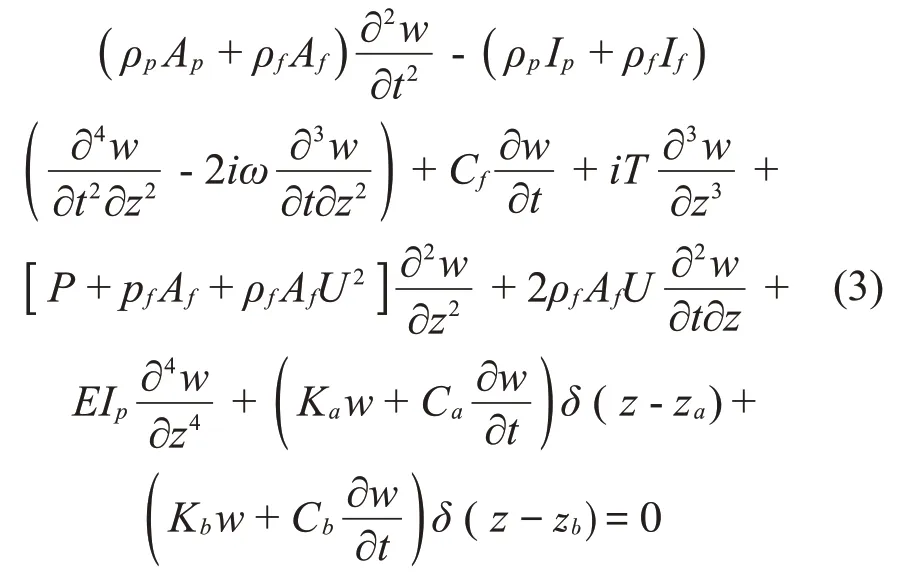
引入无量纲变量：

将上述无量纲变量全部代入方程(3)中，经化解整理可得：

2 求解方法

采用Galerkin方法对无量纲四阶偏微分方程(4)进行离散。假设任意点ξ无量纲位移可以表示为

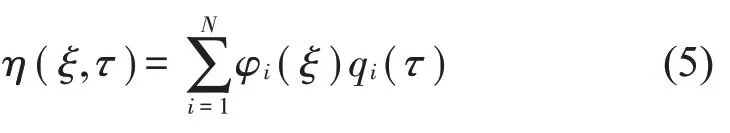
式中：qi(τ)为广义时间坐标，φi(ξ)为固定-简支梁正交模态函数，φi(ξ)的表达式为

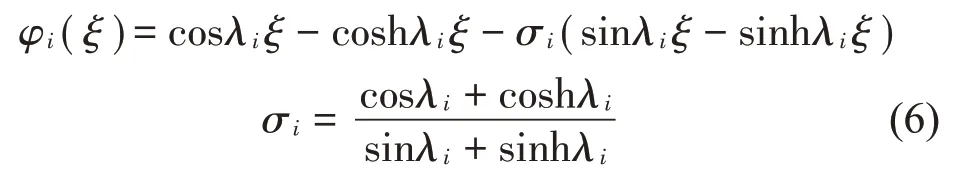
式中：特征值λi是特征方程式(7)的解。

特征方程式(7)的前10阶特征值λi列在表1中。

表1 λi的值

将式(5)代入式(4)中，并在式(4)两边同乘以jth模态函数φj(ξ)，然后对式(4)从0到1进行积分，经过化解整理可得：

式中：M=B0-γB2，C=2iγΩB2+cfB0+F=caB5+cbB6，，H=kaB5+kbB6。

其中：B0～B6的元素可表示为

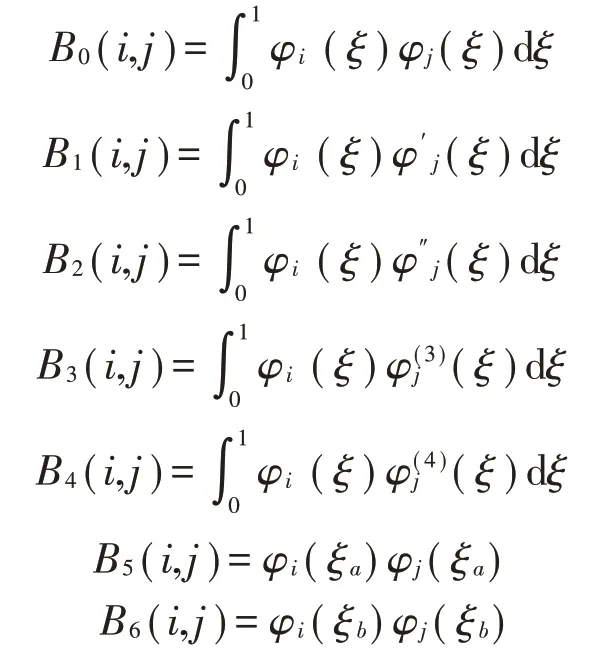
为了方便求解，引入状态向量：

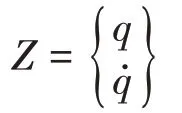
从而，式(8)由2阶微分方程转变为1阶微分方程：

取式(9)的解的形式：

式中：λ为待求的特征值，B为任意常数向量。

将式(10)代入式(9)中，假设存在特征方程(11)，则特征方程(11)有非平凡解：

其中，特征方程(11)解λ的虚部Im(λ)代表钻杆系统的各阶模态频率，而λ的实部Re(λ)符号决定钻杆系统的稳定性，当实部符号全都为负时，则系统渐进稳定；当实部符号中至少有一个为正时，则系统不稳定；当实部为零时，则系统处于临界稳定状态。

3 数值结果与分析

系统仿真参数：钻杆长度l=6 m，钻杆内径和外径分别为di=25×10-3m和de=36×10-3m，杨氏模量E=2.14×1011Pa，切削液和钻杆密度分别为ρf=0.865×103kg/m3和ρp=7.8×103kg/m3，支撑约束的初始位置为ξa=0.677和ξb=0.833，转速n=282 r/min，ω=，流速Q为切削液流量，Q=120 L/min，Π=4.28×10-5，Γ=2.65，Ka=1×107，Kb=1×108，Ca=5×104，Cb=5×105，Cf=1.72×10-5。

如图2所示。为钻杆系统模态频率随加工孔深增加的变化规律。第1阶模态频率随着孔深的增加而逐渐增大。在深孔加工过程中，选取合适的支撑位置，有助于钻杆伸入工件内依然能够保持第1阶模态频率不减小。第2阶模态频率随着孔深的增加先增大后减小。第3、第4阶模态频率随孔深的增加呈波动变化。

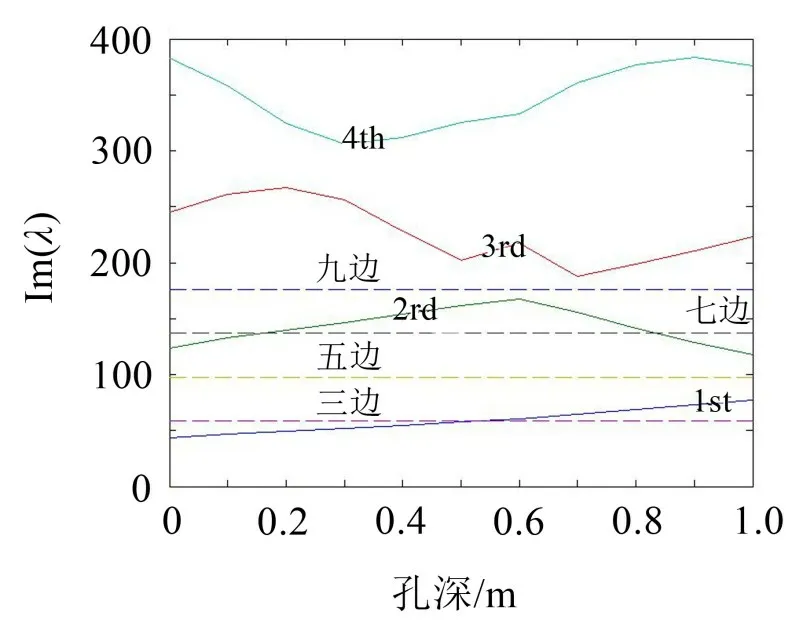
图2 前4阶模态频率随孔深增加的变化曲线

从图2可以看出1阶模态频率曲线与“三边形”虚线有一个交点，其所处的位置为0.540 6 m。2阶模态频率曲线与“七边形”虚线有两个交点，其所处的位置分别为0.155 1 m和0.839 1 m。这些交点意味着在深孔加工过程中工件内表面会产生“三边形”和“七边形”波瓣形貌。

如图3所示为前4阶实部随孔深增加的变化规律。从图3可以看出，第1阶实部呈减小的趋势，在0.6 m位置附近出现突变点，而该点位置与图2中第1阶模态频率曲线与“三边形”虚线的交点位置相近；第2阶实部先减小后增大再减小，在孔深0.7 m位置附近处为最高点；第3阶实部先增大后减小再增大，在孔深0.2 m位置附近处为最高点；第4阶实部先减小后增大。此外，在整个加工过程中前4阶的实部符号始终都为负，表明系统始终处于稳定状态。然而，各阶稳定性程度随孔深变化各不相同。

图3 前4阶实部随孔深增加的变化曲线

4 实验结果与分析

工件长度为1 060 mm，直径为74 mm，材料为40 Cr。刀头直径为44 mm，钻杆外径为36 mm，内径为25 mm。在深孔钻削过程中，选取主轴转速为282 r/min，进给量为15 mm/min。如图4所示为试验工件装夹实物图。图5为钻削试验测试系统图，采用加速度传感器采集钻杆振动信号。

图4 工件装夹

图5 钻削试验测试系统图

图6所示为在深孔加工过程中钻杆系统振动加速度信号的频谱图。钻杆的前4阶模态频率分别为15.8 Hz、41.6 Hz、60.8 Hz、85.2 Hz。

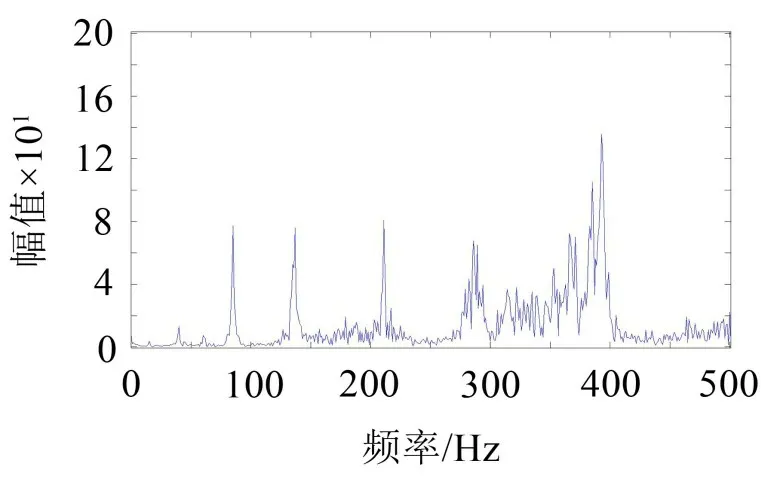
图6 钻杆系统振动加速度信号频谱图

图7所示为工件内孔表面形貌。在工件加工完成后，将内窥镜伸入工件内部，发现在工件的内表面上沿轴向明显地均匀分布着3条波瓣。本实验主轴转速为282 r/min，将该数据转换成频率为4.7 Hz，其接近于钻杆系统一阶模态频率的1/3，因此，实验结果与所建立的钻杆系统模型仿真分析结果较为吻合。

图7 工件内孔表面形貌

5 结语

本文建立了钻杆系统动力学模型，分析了钻削深度对系统固有频率和稳定性的影响。在深孔加工过程中，钻杆系统各阶模态频率随孔深的变化规律并不相同。此外，这种变刚度现象会对深孔加工稳定性和工件质量产生一定的影响，而且会直接影响内孔表面的波瓣形貌，这与系统第1阶固有频率有着密切的关系，从仿真结果和实验结果也可同时得到验证。