低雷诺数下的Ahmed模型绕流流场结构分析

张彦杰，张光德， 严运兵, 朱冬涛，周文韬

(武汉科技大学汽车与交通工程学院，湖北 武汉，430065)

汽车在行驶过程中所受气动阻力对其油耗影响较大。从阻力产生的机理来看，气动阻力主要由压差阻力、诱导阻力及干涉阻力构成，其中压差阻力主要来自汽车尾部[1]，而诱导阻力及干涉阻力均与车辆周围的涡结构密切相关，与尾涡相关的气动阻力占汽车所受总气动阻力的40%左右[2]，因此，研究车辆周围的涡系结构对于车辆减阻的重要性不言而喻。

1984年，Ahmed等[3]提出一种典型的钝体模型(Ahmed模型)用于研究汽车周围流场结构与气动阻力，自那时起，该模型一直是研究陆地车辆各种气动特性的最通用模型。基于Ahmed模型，Thacker等[4]研究了雷诺数(Re)为2.2×106条件下模型斜面上部流场的分离与附着结构； Zhang等[5]通过研究尾部倾角为25°的Ahmed模型在Re为(0.45～2.4)×105条件下的流场结构，获得了其外部流线拓扑结构；Tunay等[6]考察了尾部倾角为25°的Ahmed模型在Re为1.48×104时的尾迹区域流场结构，并分析了该区域的流场特性；Akira等[7]讨论了Re为7.44×104时，具有30°尾部倾角的Ahmed模型尾迹区域处两种分离涡与气动阻力的关系；杨小龙等[8]在Re为2.7×106条件下研究了Ahmed模型尾部倾角对于整车力学系数、尾迹区域流场结构与压力分布的影响；杨志刚等[9]在Re为2.81×106条件下比较了4种不同的湍流模型对MIRA(motor industry research association)模型外部流场的预测能力；张英朝等[10]研究了Re为4.48×104时射流孔的位置、孔径、喷射角度等参数对尾部倾角为25°的Ahmed模型外部流场结构的影响，从而确定了可获得最小阻力系数的喷射口配置。此外，王冰心等[11]利用大涡模拟(LES)成功预测了Re为7.78×105时类车体尾迹区域的涡系结构与流场特性，并论证了大涡模拟用于流场研究的可靠性；范亚军等[12]借助风洞试验研究了方背Ahmed模型在Re为9.98×104条件下的非定常尾迹流动特征；张勇等[13]采用计算流体力学(CFD)方法预测了较高Re(2.24×106)条件下不同模型尾部参数对尾迹流场结构的影响，从而确定了气动阻力最低模型的几何参数。鉴于实验和仿真均能有效反映类车体模型周围的流场特征且LES在流场数值模拟研究中应用较广[14-15]，本文利用LES方法对Ahmed模型的绕流流场进行数值模拟，通过分析该模型周围不同位置处流场参数的时变信息以及监测点的速度频谱来研究模型周围的非定常流场特性并探讨Ahmed模型周围涡系结构的演化规律。

1 数值仿真模型与模拟方法

1.1 数值仿真模型

基于文献[6]所报道的较低Re(1.48×104)条件下的Ahmed模型外部流场水洞实验，采用LES方法对该类车体模型的绕流流场进行数值模拟。模型尾部倾角为25°，长(L)、宽(W)、高(H)分别为261、97.25、72 mm，模型具体几何参数如图1所示，其中x轴沿模型长度方向(流向)，z轴沿模型宽度方向(展向)，y轴沿模型高度方向(垂向)，以类车体底面尾端宽边中点为坐标原点o。在数值模拟过程中，计算域尺寸与文献[6]中的水洞尺寸相同，为2.088 m×0.36 m×0.36 m，类车体Ahmed模型车头距离计算域入口0.522 m，车尾距离计算域出口1.305 m(见图2)。

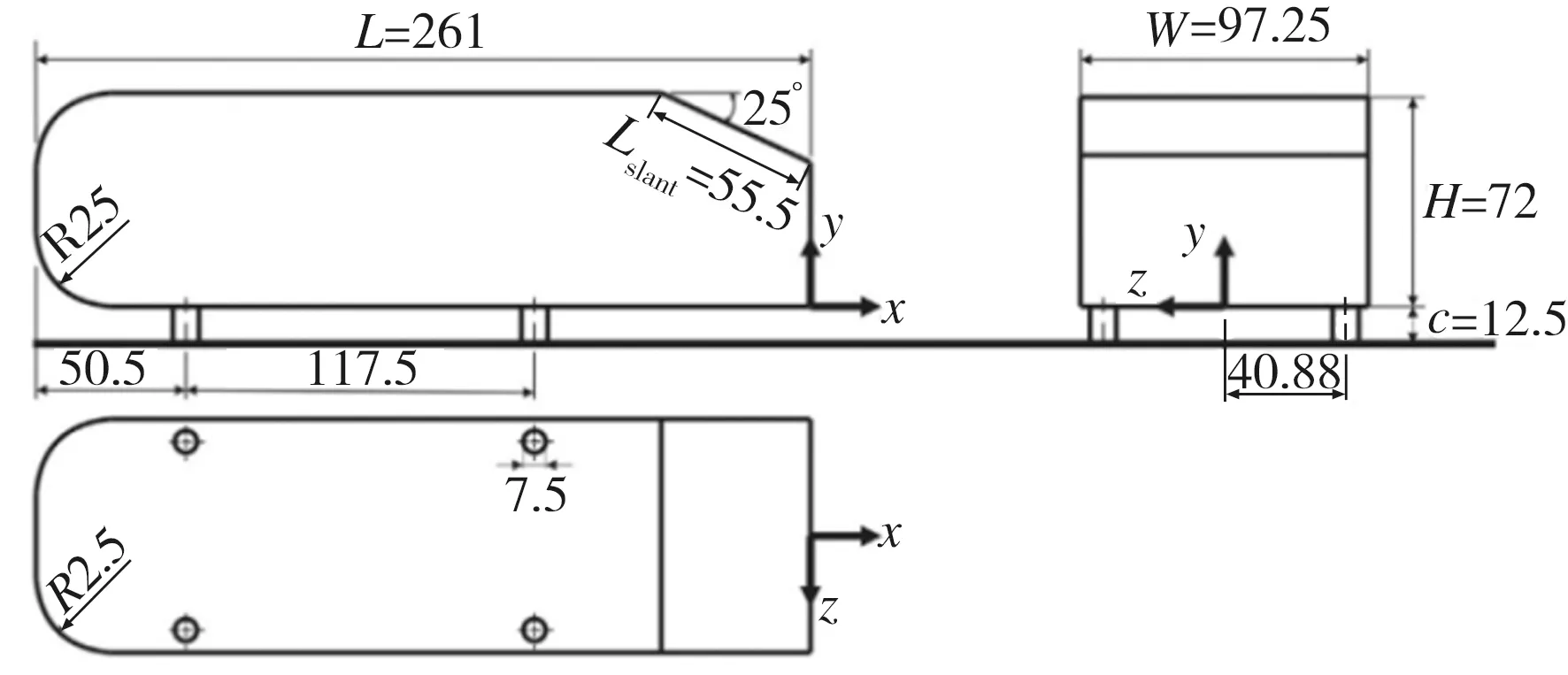
图1 Ahmed模型几何参数

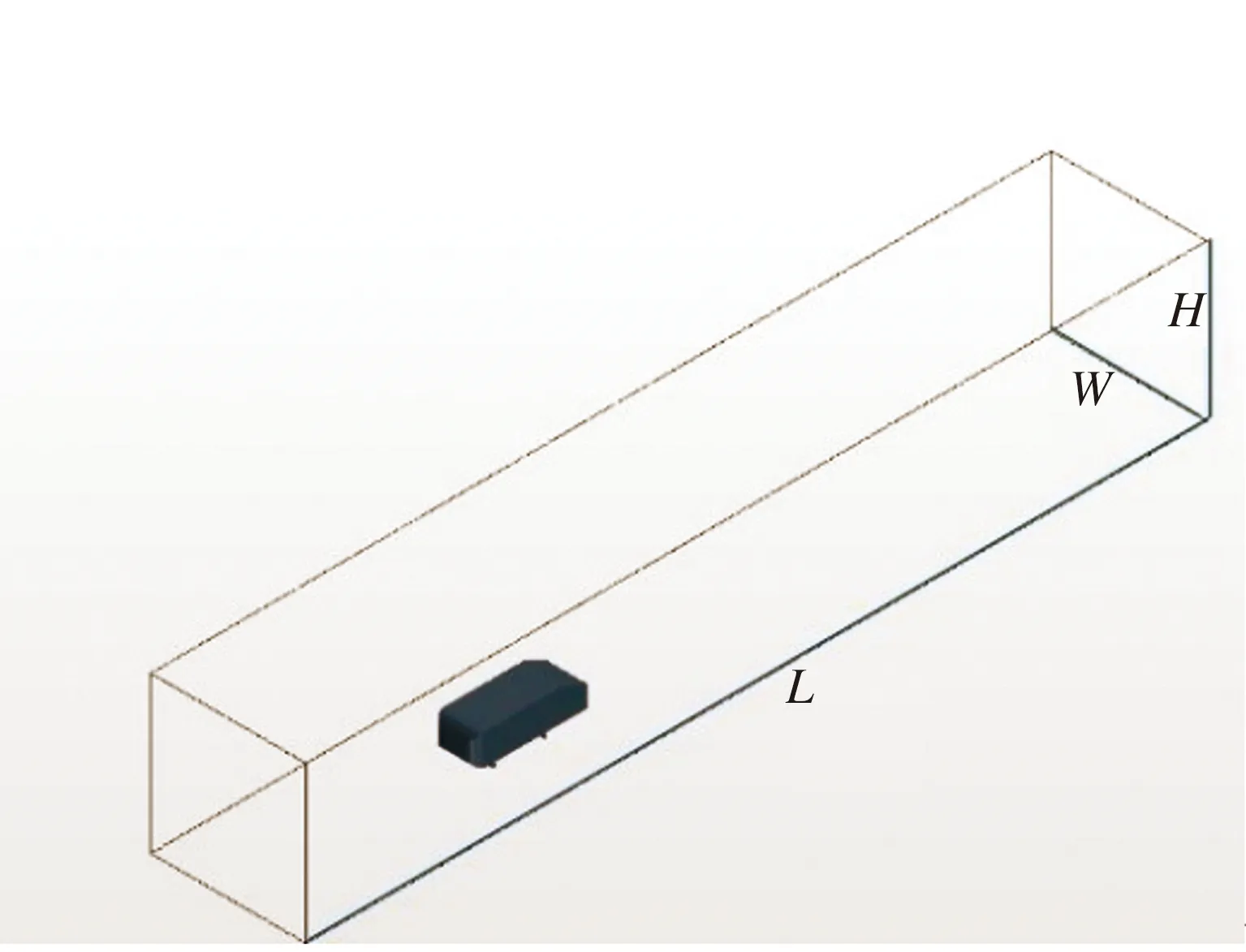
图2 计算域

利用Ahmed模型高度H(72 mm)对空间三维坐标x、y、z进行无量纲化处理，相应表达式为：

(1)

采用笛卡尔网格划分计算域内部，同时对Ahmed模型周围以及模型的尾迹区域进行细化，在车身表面沿法线方向向外依次构建5个边界层，紧贴车身表面的第1层边界厚度为0.5 mm，第2～5层边界厚度均为前一层边界厚度的1.1倍，Ahmed模型周边沿计算域长度方向的中截面xoy(z*为0)网格结构如图3所示。此外，调整网格尺寸以确保壁面参数Y+值不高于1.9，在本研究中，计算域网格总数为806万，相应壁面参数Y+值云图见图4。

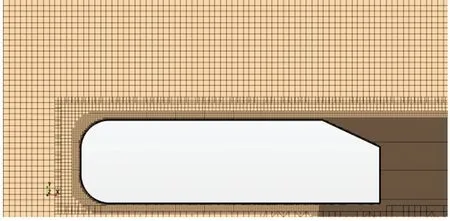
图3 网格结构

图4 Y+值云图

1.2 数值模拟方法与流场参数

借助STAR-CCM+仿真平台模拟流场结构，湍流模型采用LES框架中的动态Smagorinsky亚格子模型。涡黏系数μt的计算公式为：

μt=ρΔ2S

(2)

式中，ρ为密度，Δ2为变量函数，S为平均应变率张量，Δ2和S的表达式分别为：

(3)

(4)

式(3)～式(4)中，CS是Smagorinsky亚格子模型常数，默认值为3.5；V为体积微元；为Hamilton算子；为平均速度。模拟计算所涉及的主要边界条件如表1所示。

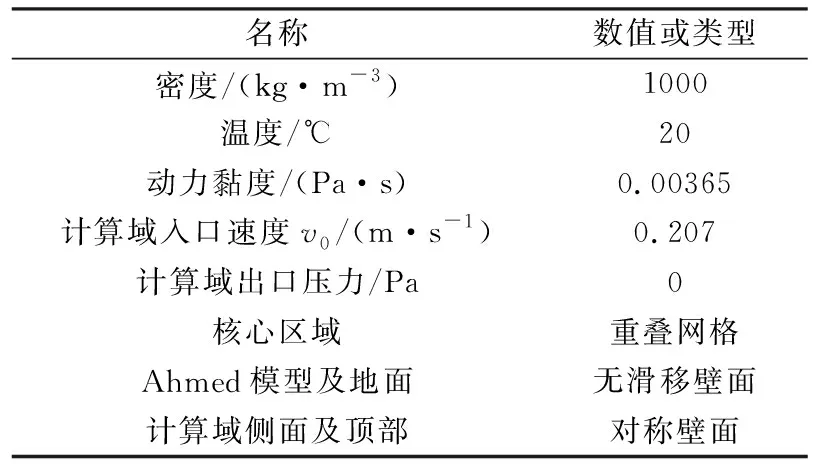
表1 边界条件

在模拟过程中，时间步长为1×10-3s，对单位时间步长进行25次迭代，每个时间步长内残差均可收敛至1×10-3。整个模拟过程共经历23000个时间步长，折合物理时间23 s，对最后10000个时间步长即物理时间第13～23 s期间的模拟结果进行统计以获得相关流场信息，其中借助所得流场时均流线图可分析类车体Ahmed模型周围区域的流场结构；通过对模型尾部区域流场时均模拟结果进行分析可获得该区域涡系结构特征，再基于涡系结构选取监测点进行频谱分析有助于明确相应流场的非定常特性，同时，对模型非尾部区域涡系结构进行频谱分析以追溯模型前端来流与尾迹区域流场的关系及演化过程，最终可获得Ahmed模型周边的整体流场结构。对整个模拟过程进行计算共耗时432 h，计算环境为Xeon E5-2630 CPU平台40核并行。

1.3 数值模拟方法初步验证

为验证本文LES数值模拟方法的有效性，将利用该法所得Ahmed模型周围区域时均速度分布与文献[6]利用粒子图像测速(PIV)技术所得相应的实验结果进行对比，图5所示为模型尾迹区域特定位置流向时均速度u与垂向时均速度w分布的模拟结果与实验结果对比情况。由图5可见，在Ahmed模型尾迹区域不同高度截面处流向速度与垂向速度的数值模拟结果均与相应的实验结果基本吻合，表明本文所用LES数值模拟方法有效可行。

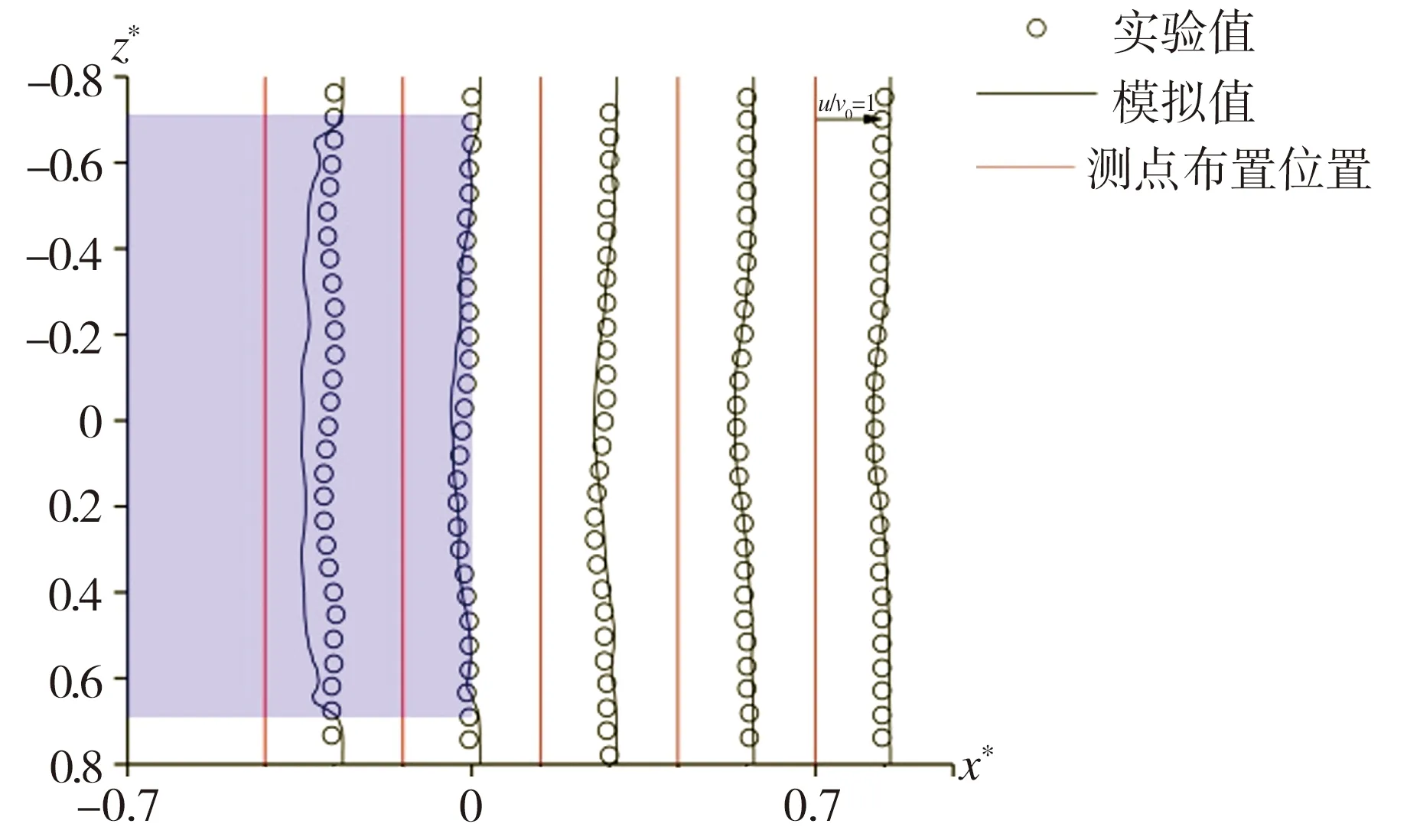
(a) y*=1，流向速度分量

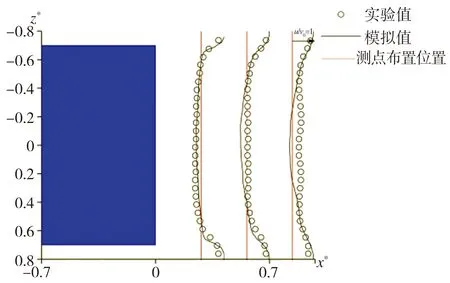
(b) y*=0.14，流向速度分量

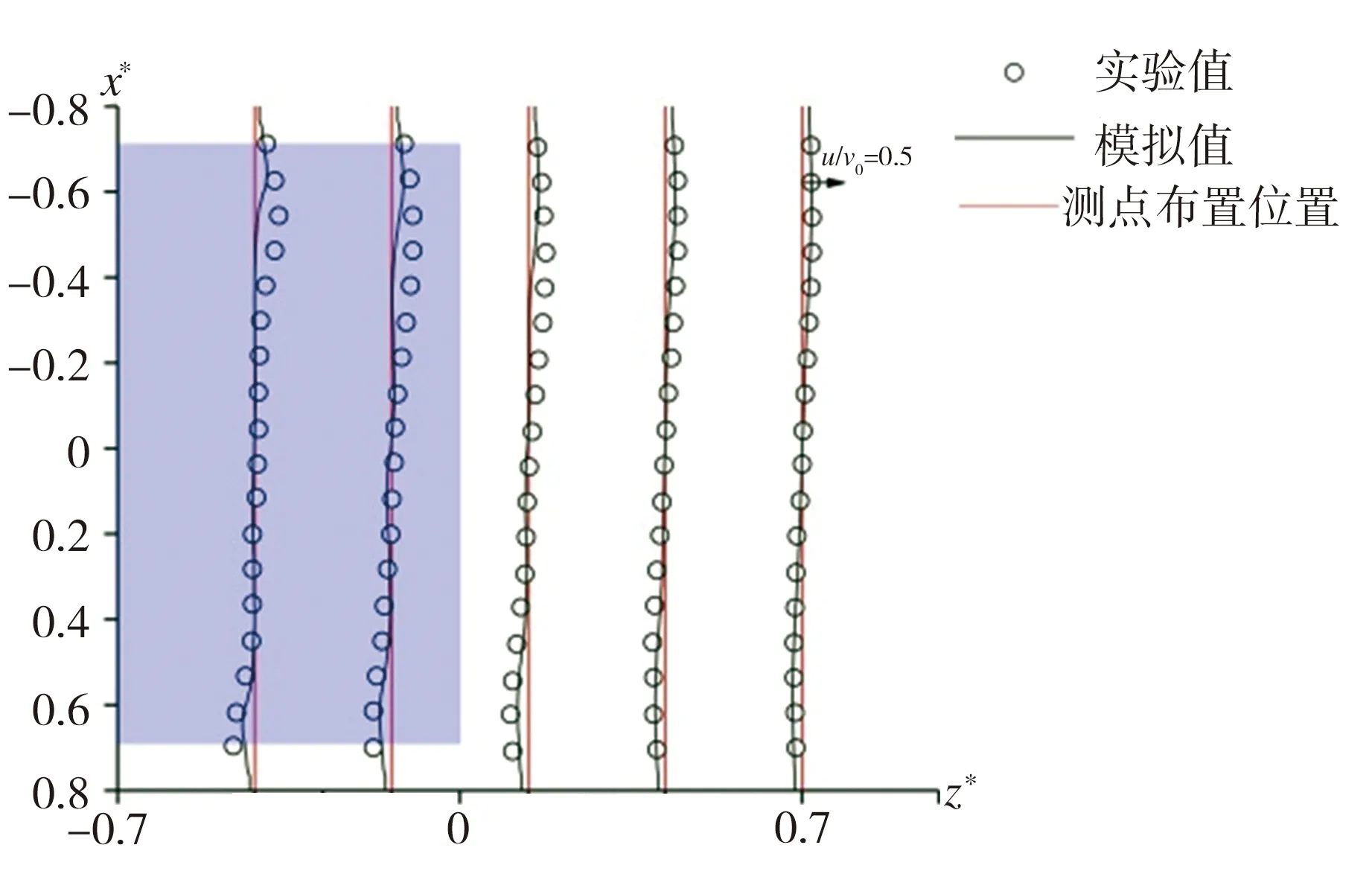
(c) y*=1，垂向速度分量

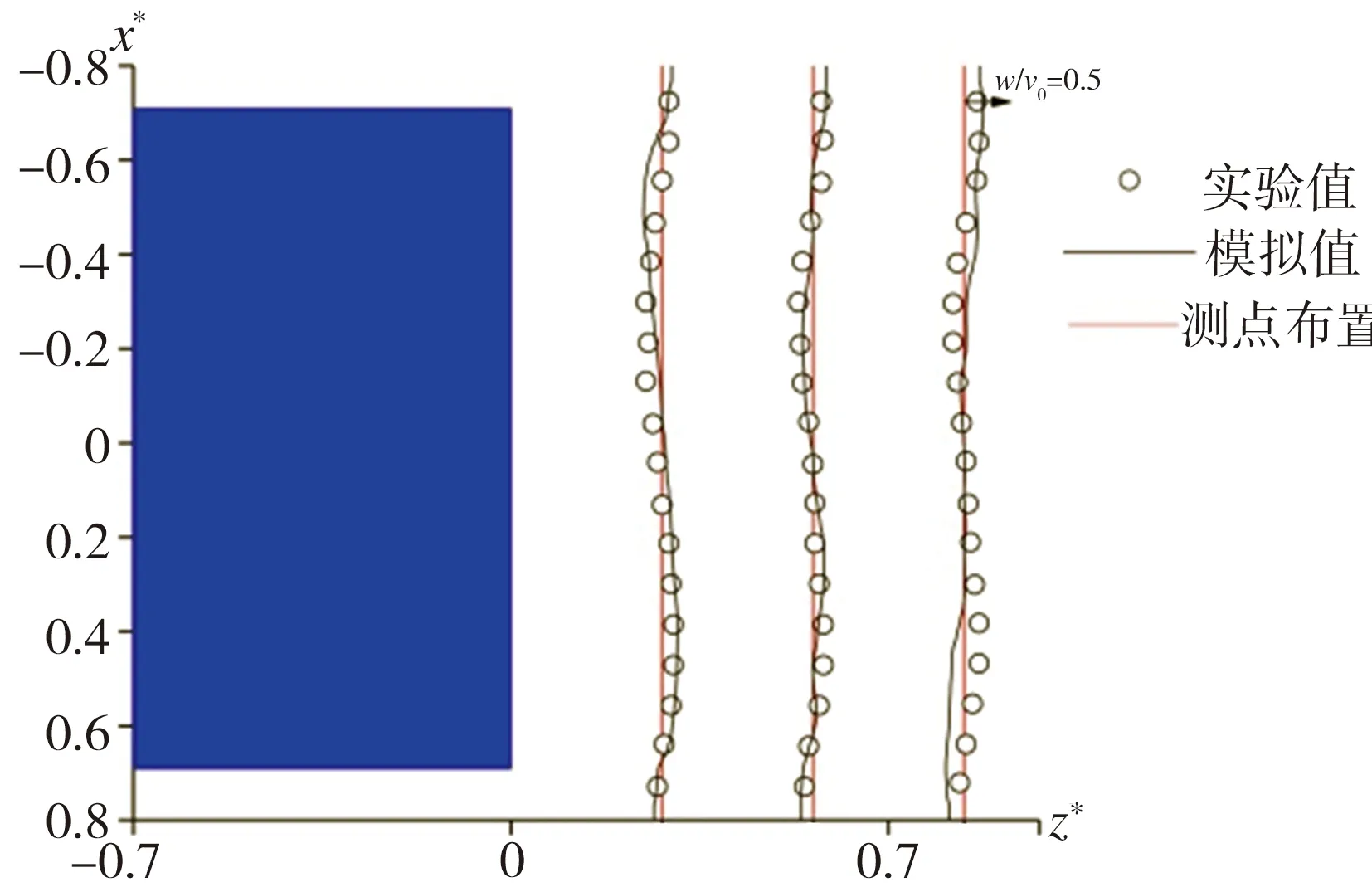
(d) y*=0.14，垂向速度分量

2 数值模拟结果与分析

2.1 时均流线图分析

在Ahmed模型周围不同高度水平截面(y*分别为1、0.89、0.78、0.67、0.35、0.14)处的流场时均流线分布数值模拟结果如图6所示。从图6中可以看出，分布于Ahmed模型周围不同高度水平截面处的流场大体上都以z*为0的中截面xoy为对称面，并且模型前部与尾迹区域均存在明显的涡系结构，在y*为0.89的水平截面模型尾部区域可捕捉到流线分叉线(图6(b))，而y*分别为0.78和0.67的水平截面(图6(c)～6(d))上则出现了较复杂的流场结构，其中在靠近模型前端及尾迹区域的流场均存在1对关于中线(z*为0)对称的焦点，在模型尾迹区域中心地带还能清晰地捕捉到分叉线与鞍点。当水平截面高度降至y*为0.35处时，靠近模型尾迹区域的流场除了1对关于中线对称的焦点外，还存在1个鞍点和1个节点(图6(e))。进一步降低水平截面高度，由图6(f)可见，在接近模型底面的截面(y*为0.14)上，模型尾迹区域流场中心部位存在1个节点，同时在该节点附近靠近尾迹区域边缘处还捕捉到1个单独的焦点。综合分析上述时均流线图可以推断，在模型两侧靠近前端的流场区域存在1对侧向涡，大致位于y*为0.67～0.78这一高度区间；而模型尾迹区域的来流情况较为复杂，首先在模型尾部倾斜表面上方存在2种涡团，一种是存在于该处中间位置的分离泡，另一种则是在模型尾部倾斜表面与侧面交汇处产生的1对关于xoy面(z*为0)对称的C柱涡；此外，在近尾迹区域还存在一对较大的关于xoy面(z*为0)对称的分离泡。

(a)y*=1

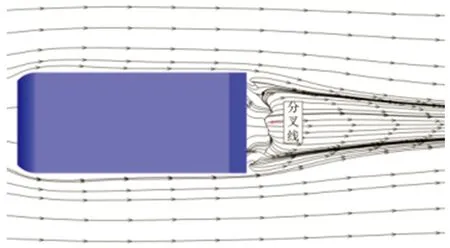
(b)y*=0.89

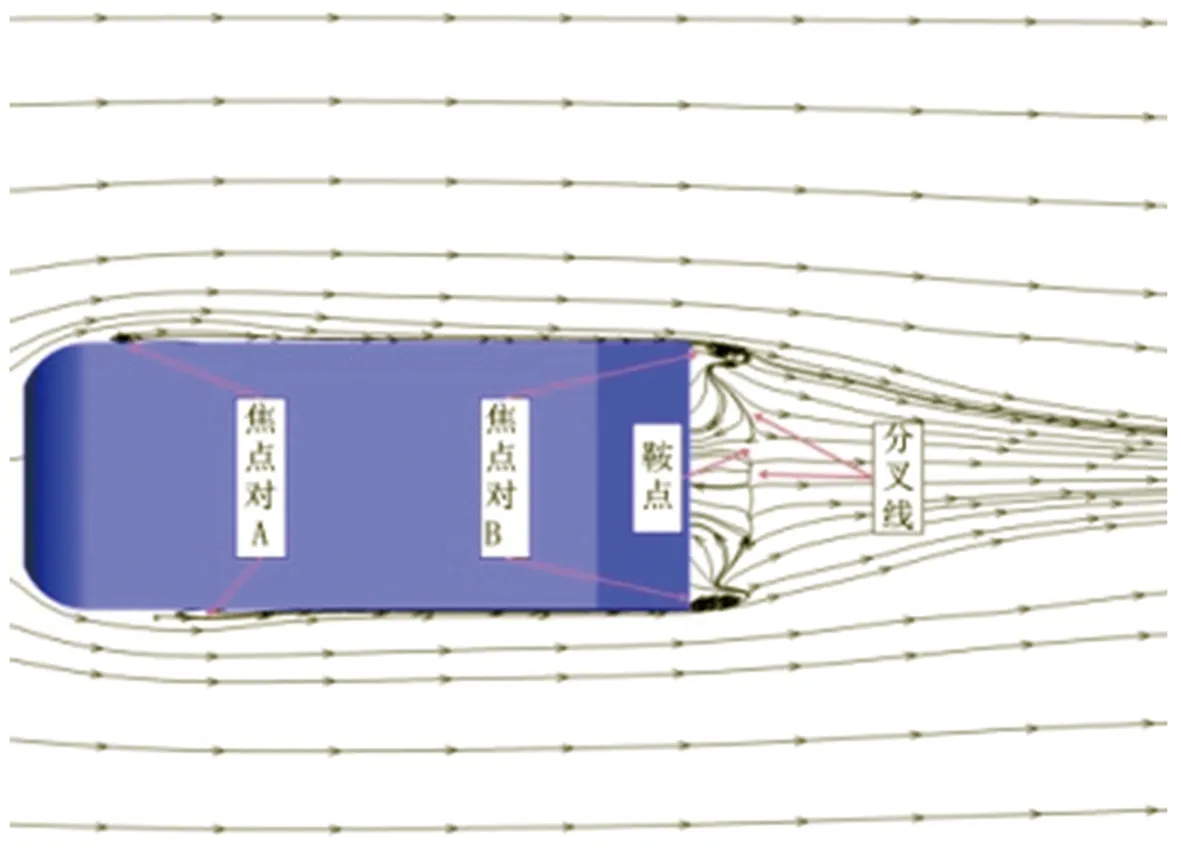
(c)y*=0.78

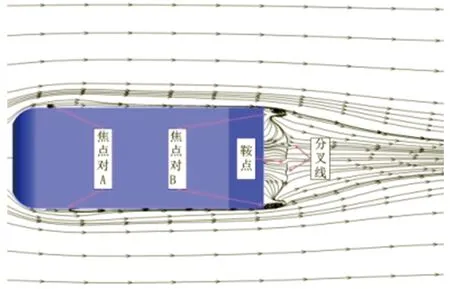
(d)y*=0.67

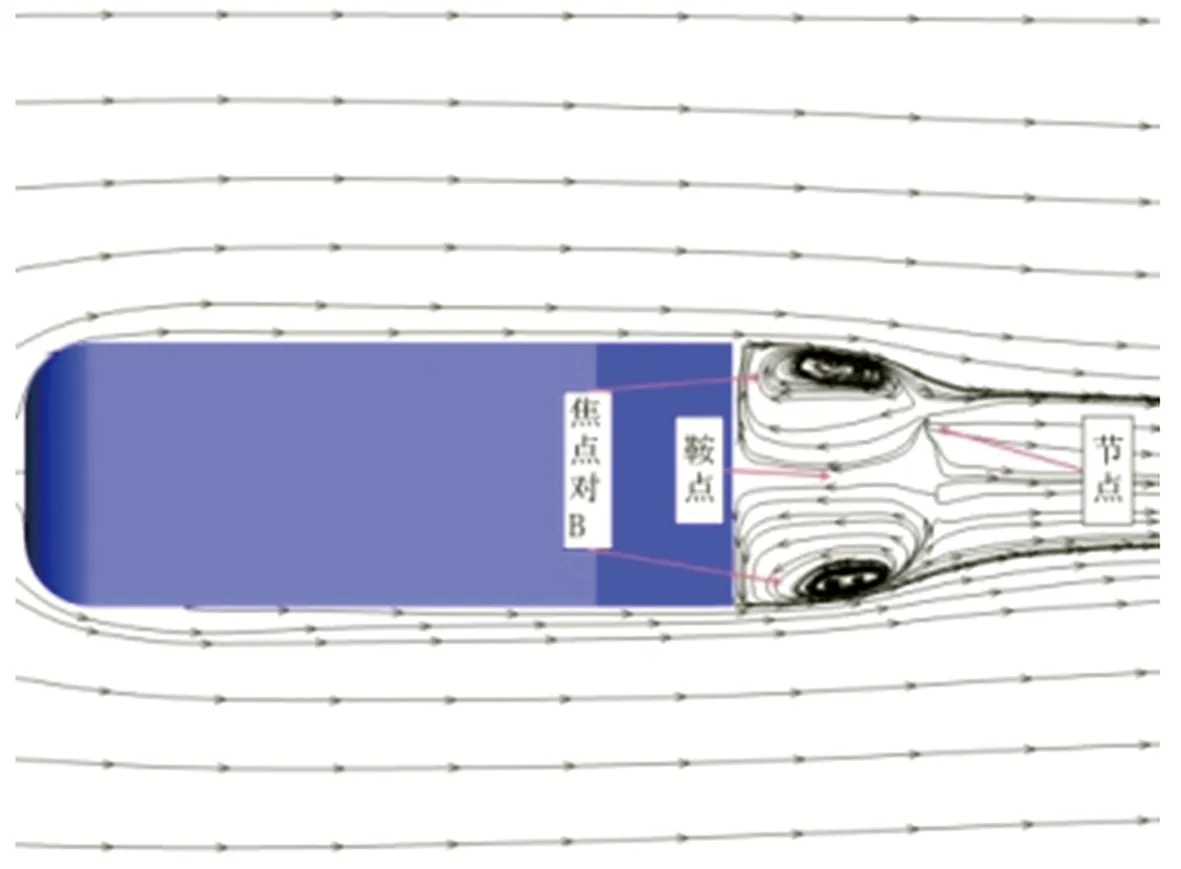
(e)y*=0.35

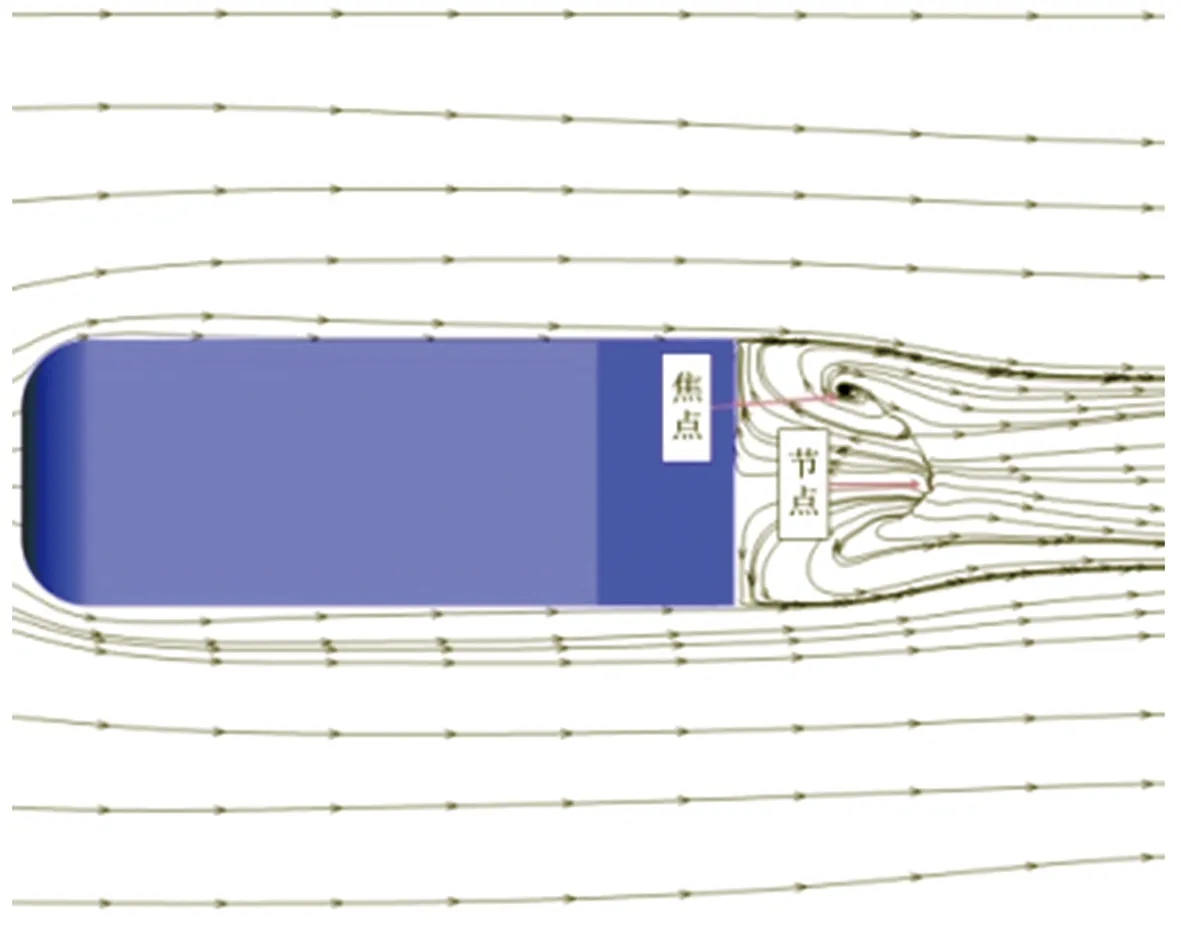
(f)y*=0.14

2.2 模型尾部区域流场的非定常特性

2.2.1 模型尾部倾斜表面上方流场的非定常特性

在模型尾部倾斜表面附近y*为1的水平截面上分别布置A1～A5(x*均为-0.59)、B1～B5(x*均为-0.21)、C1～C5(x*均为0)3横排共计15个监测点，每排监测点按序号1～5所对应的z*值依次为0、0.16、0.34、0.42、0.68，监测点具体布置情况以及根据模拟期间第13～23 s所收集流场流向速度信息做出的各监测点处流场功率谱密度曲线如图7所示。由图7可见，在模型尾部倾斜表面上方不同监测点处流场功率谱密度分布的主要特征基本相同，如A3、A4、B3、B4、C1、C2、C3、C4监测点处的流场功率谱密度曲线均出现了与相应位置涡结构对应的Strouhal数(St)为0.107的特征峰，其中以z*为0.42的监测点处最为明显，该特征峰强度随着z*值的减小呈不断减弱趋势，在x*不为0、z*均为0.16的A2、B2处已然消失，不过在x*为0、z*为0的C1处仍能观察到St为0.107的特征峰，这是因来流的剪切层在倾斜表面上方分离并卷曲形成了分离泡所致。流场功率谱密度曲线中还出现了St为0.214的特征峰，对应模型尾部倾斜表面与侧面交界附近z*为0.68的A5、B5、C5处的涡结构，并且该峰沿流向方向更趋于明显，这与文献[11]通过对Ahmed模型尾迹区域压力进行频谱分析所得结果类似，据该文献报道，在Re为7.78×105的条件下，流场中出现的C柱涡所对应的特征峰St为0.3。文献[11]中C柱涡出现的位置与本研究基本一致，同时，该文献还指出，此类C柱涡产生的原因可能是：模型顶部来流在倾斜表面上方边缘分离并产生低压区域，使得侧面来流在倾斜表面侧边位置形成压差，导致来流向内卷曲产生C柱涡，而C柱涡的诱导作用又造成顶流沿斜面下洗，从而影响尾迹区域的流场结构。

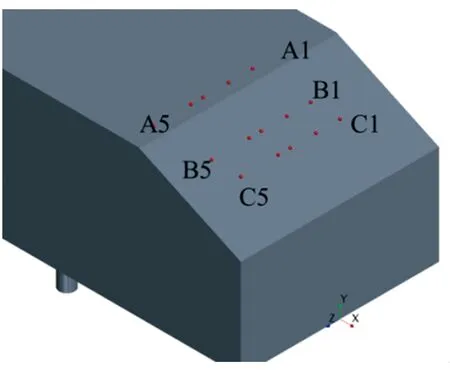
(a) 监测点分布

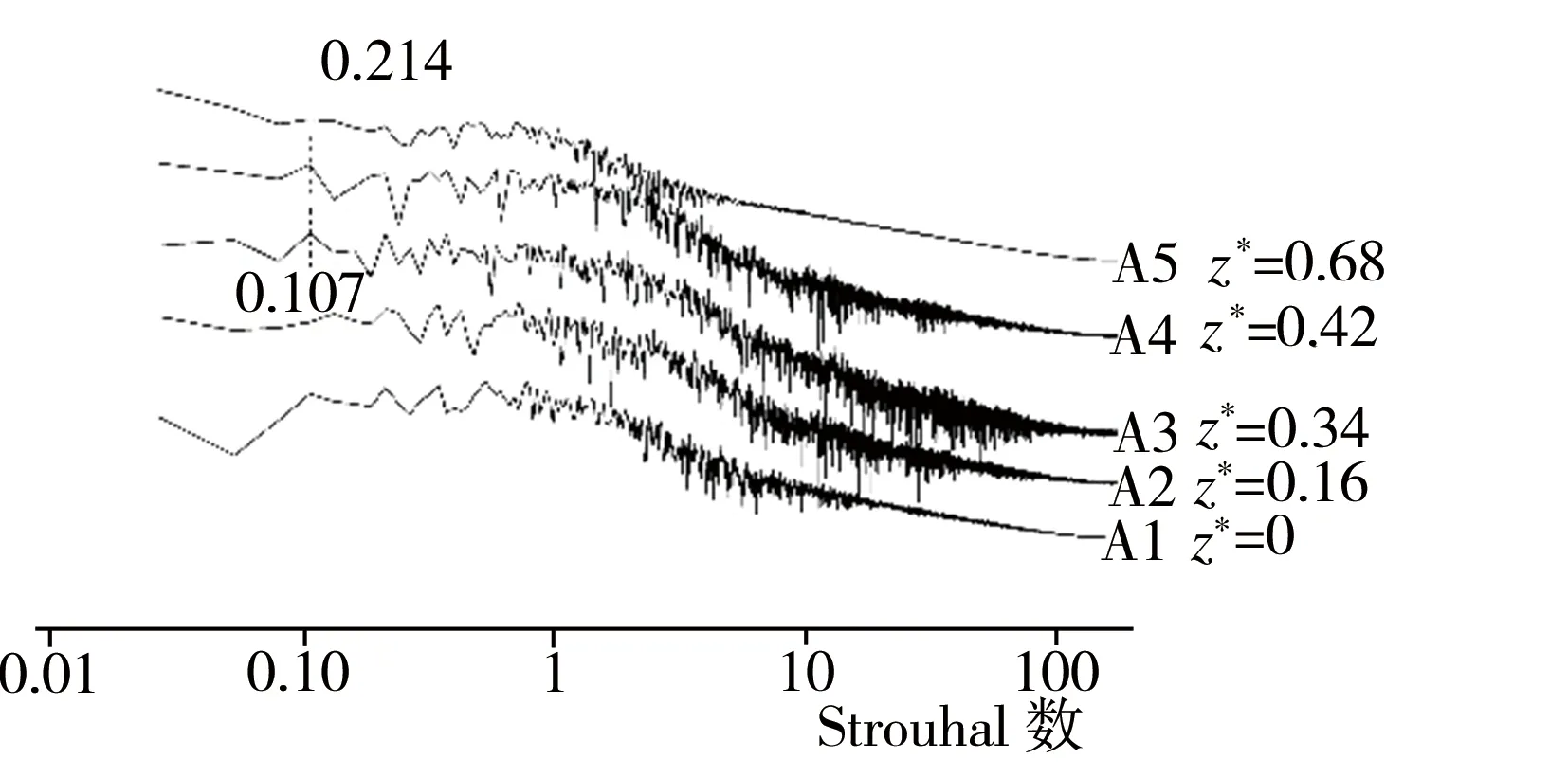
(b) A1～A5(x*为-0.59)功率谱密度

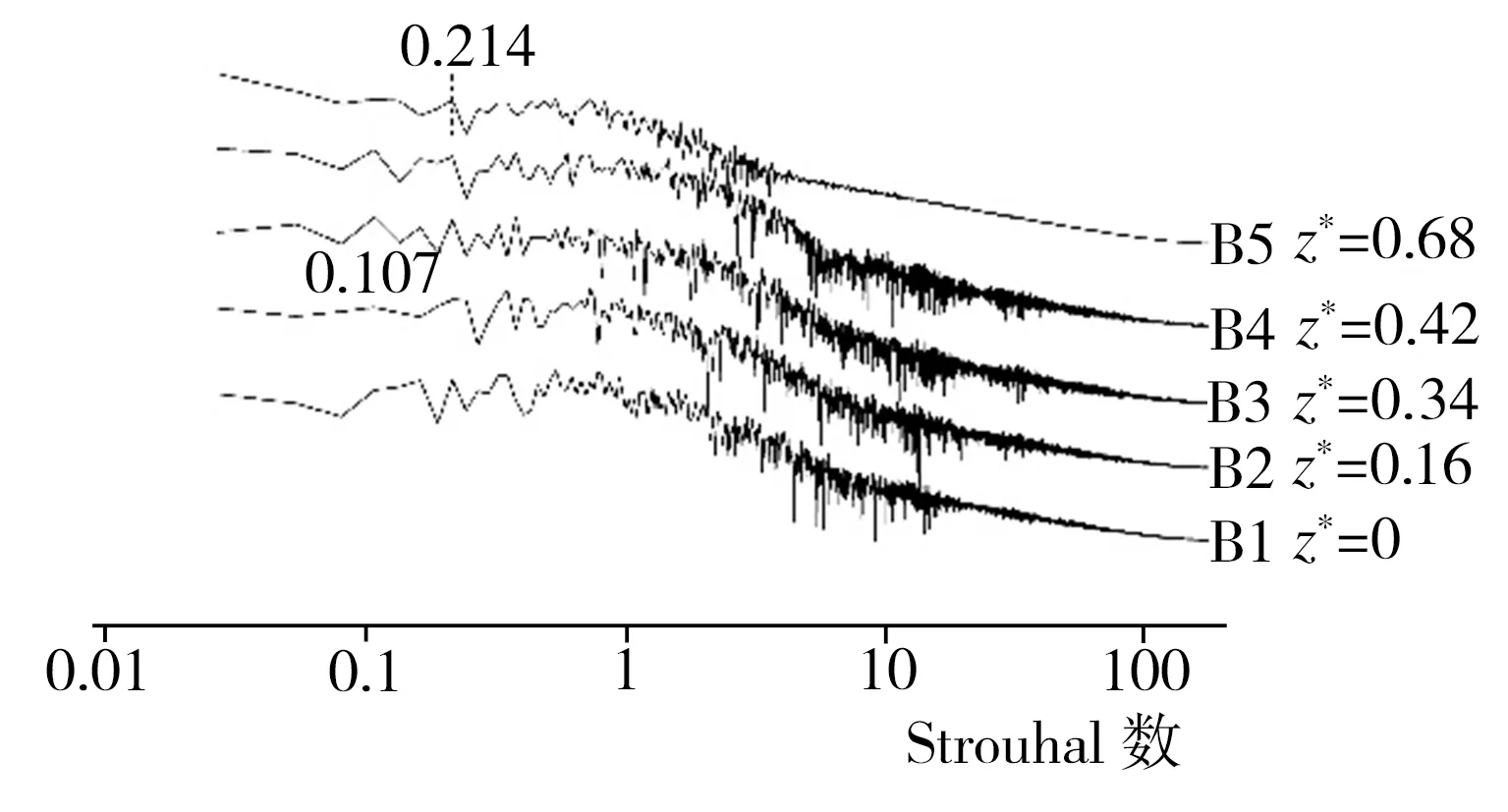
(c) B1～B5(x*为-0.21)功率谱密度

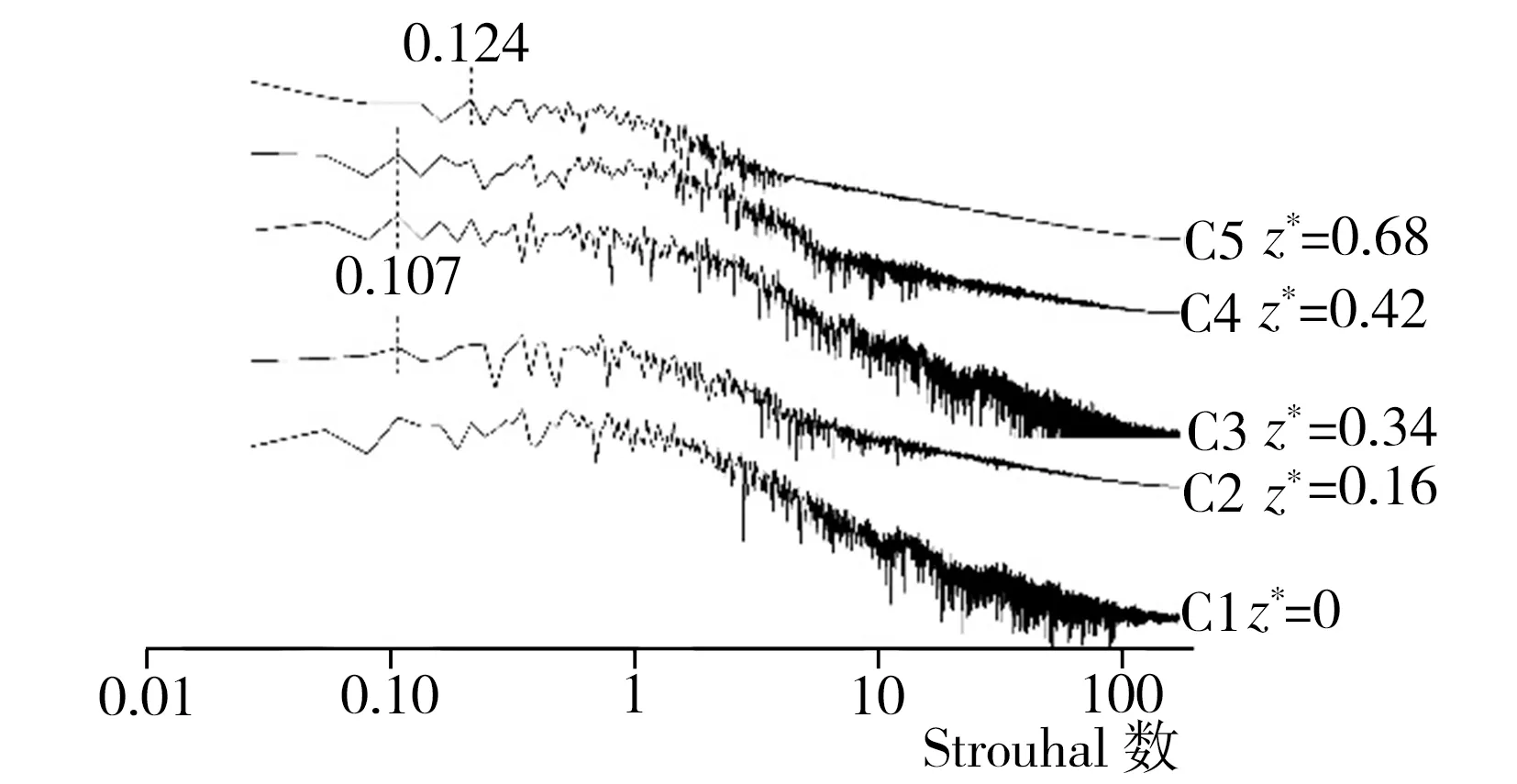
(d) C1～C5(x*为0)功率谱密度

2.2.2 模型尾迹中心区域流场的非定常特性

在模型尾迹中心区域z*为0的中截面xoy上分别布置D1～D5(x*均为0.46)、E1～E5(x*均为0.92)、F1～F5(x*均为1.84)3竖排共计15个监测点，每排监测点按序号1～5所对应的y*值依次为0、0.10、0.21、0.32、0.64，监测点具体布置情况以及根据模拟期间第13～23 s所收集流场流向速度信息做出的各监测点处流场功率谱密度曲线如图8所示。由图8可见，在x*均为0.46的D3、D4、D5处监测到体现相应涡结构的St为0.133的特征峰，尤其以y*为0.21的D3处最为明显，但随着高度降低，在x*同为0.46的D1(y*为0)和D2(y*为0.10)处已很难观察到特征峰的存在。而靠近尾迹下游区域x*均为0.92的E1～E5处流场功率谱密度分布监测结果与D1～D5处类似，在y*值较小的2个监测点E1和E2没有出现对应监测点处涡结构的特征峰，当高度升至E3(y*为0.21)处时才观测到与该处涡结构对应的St为0.133的特征峰，不过，继续升高至E4(y*为0.32)位置时，对应该处涡结构的特征峰St变为0.107，而最高处y*为0.64的E5监测点则又出现了St为0.133的特征峰。至于在模型尾迹区域距模型较远的F1～F5监测点(x*均为1.84)，除了位置最低的F1(y*为0)以外，其余监测点均能观测到与相应涡结构对应的St为0.133的特征峰。

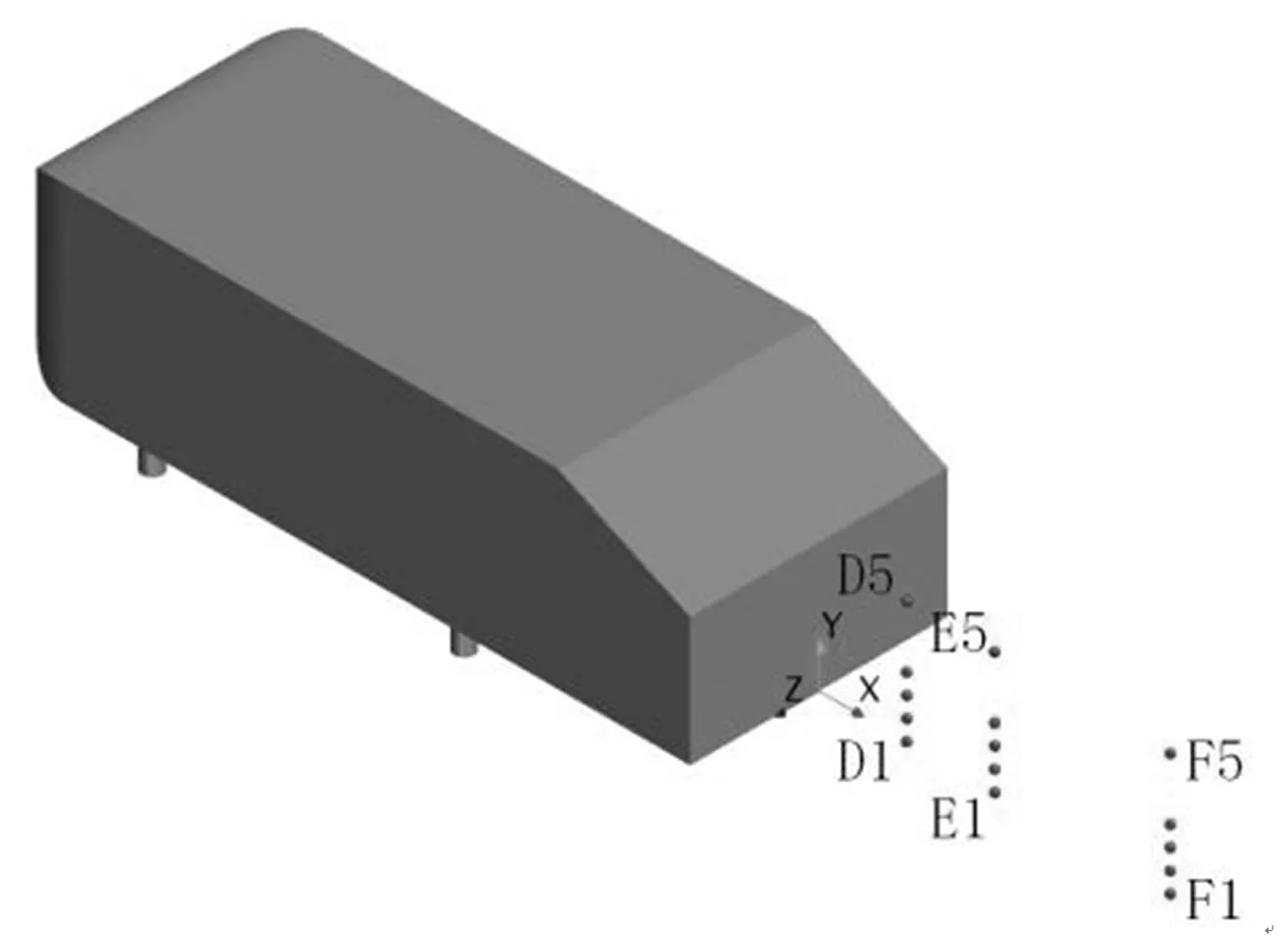
(a) 监测点分布

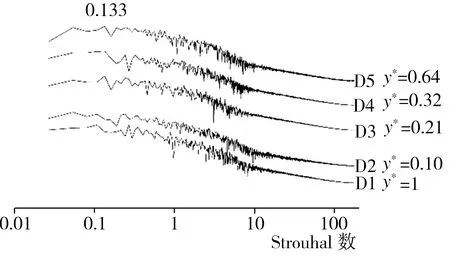
(b) D1～D5(x*为0.46)功率谱密度

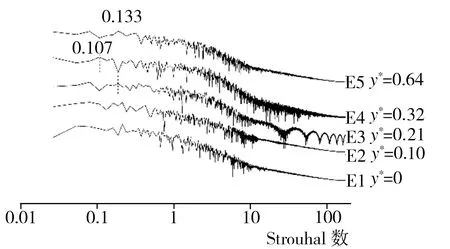
(c) E1～E5(x*为0.92)功率谱密度

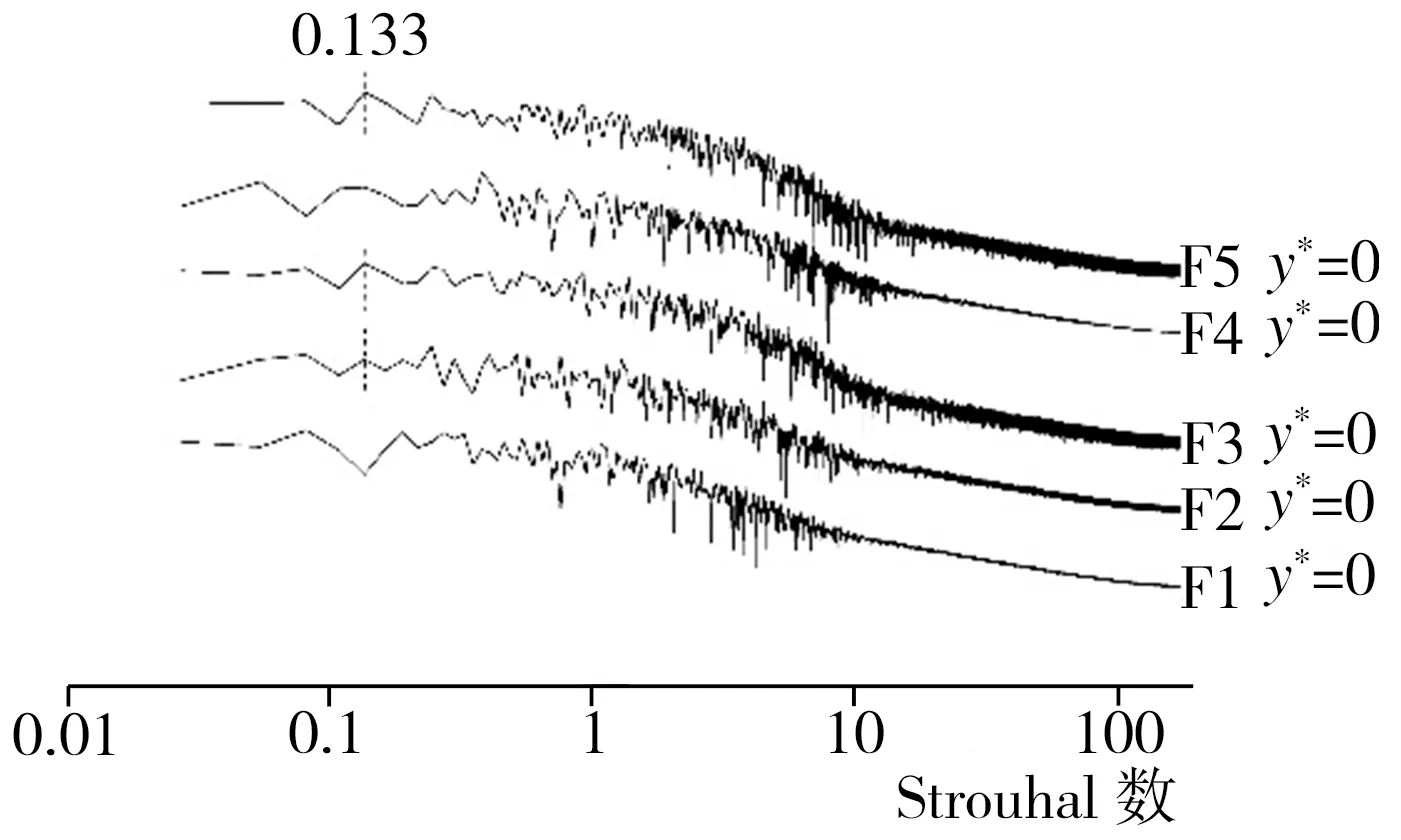
(d) F1～F5(x*为1.84)功率谱密度

为了探究模型尾迹区域涡系结构的三维特性，再分别以D1～D5、E1～E5、F1～F5在z*为0.52、0.67且与中截面xoy平行的两个纵向截面上的垂直投影点为监测点，相应标注为G1～G5、H1～H5、I1～I5以及J1～J5、K1～K5、L1～L5，监测点具体布置情况以及根据模拟期间第13～23 s所收集流场流向速度信息做出的各监测点处流场功率谱密度曲线如图9所示。由图9(a)～9(d)可知，在z*为0.52的纵截面上出现的主要功率谱密度特征峰St为0.133，这与中截面处的模拟结果相同，不过，当x*为0.46时，在中截面上位置较低的D1(y*为0)和D2(y*为0.10)处很难观察到St为0.133的特征峰，而在z*为0.52的纵截面上与D1高度相同、最接近地面的G1处即可监测到该峰的存在，并且随着监测点高度的增加，St为0.133的特征峰在与D2高度相同的G2处最为明显，之后在更高的监测点处虽然仍能观测到该峰，但峰强度已略有减弱；当x*增至0.92时，相应H系列监测点处出现了包括St为0.133的特征峰在内的多种功率谱密度特征峰，其中，除了在位置最低的H1(y*为0)处没有监测到明显的与该处涡结构对应的特征峰外，随着监测点高度的增加，在H2(y*为0.10)处出现了St为0.107的特征峰，而在H3(y*为0.21)处则首次出现St为0.133的特征峰，当高度升至H4(y*为0.32)处时，相应特征峰的St变为0.080，最后，在位置最高的H5(y*为0.64)处再次出现St为0.133的特征峰；当监测点距类车体模型尾部较远(x*为1.84)时，在I2(y*为0.10)、I3(y*为0.21)、I5(y*为0.64)处均观察到了St为0.133的特征峰，而在I1(y*为0)和I4(y*为0.32)处出现的特征峰St则分别改变为0.107、0.160。至于紧贴类车体模型侧面、z*为0.67的纵截面，由图9(e)～9(f)可见，该截面与z*为0的中截面及z*为0.52的纵截面涡系结构特征不同，前者存在的主要特征峰St分别为0.668、0.692等，其中，当x*为0.46时，在J2(y*为0.10)、J3(y*为0.21)处均监测到了St为0.668的特征峰，在位置较高的J4(y*为0.32)处所监测到的特征峰St变为0.692，而位置最高的J5(y*为0.64)处又出现了St为0.668的特征峰；当x*为0.92时，K3(y*为0.21)及K5(y*为0.64)处的特征峰所对应的St均为0.668，而K4(y*为0.32)处则出现了St为0.615的特征峰；在尾迹区域下游位置(x*为1.84)所监测到的多数特征峰St均为0.160，主要分布在L2(y*为0.10)、L3(y*为0.21)及L5(y*为0.64)处，此外，L1(y*为0)和L4(y*为0.32)处特征峰所对应的St分别为0.133、0.240。因xoy面为中截面,所以上述监测点处的涡结构在z*负方向也关于xoy面呈对称分布。

综合上述类车体模型尾迹区域流场频谱分析结果表明，该区域存在两种主要的涡系结构，其中一种是分布范围较广的分离泡，所占据的空间位置沿流向从x*为0.46处一直延伸至x*为1.84处，沿展向从对称中面(z*为0)处开始向侧面延展并最终到达|z*|为0.52处，沿垂向则从y*为0处直达y*为0.64处，该类涡结构所对应的St为0.133，应是尾部斜面下洗流与底部上洗流相互作用所致；另一种涡系结构主要存在于靠近区域侧边界的纵截面(z*为0.67)上部位置，其功率谱密度曲线特征峰所对应的St为0.668，该涡系结构产生的机理可能与C柱涡产生机理相似，是因模型尾迹区域中部产生分离泡而造成该处压强低于侧面来流压强，导致侧面来流流至尾迹区域后端时向内卷曲从而形成新的涡系结构。

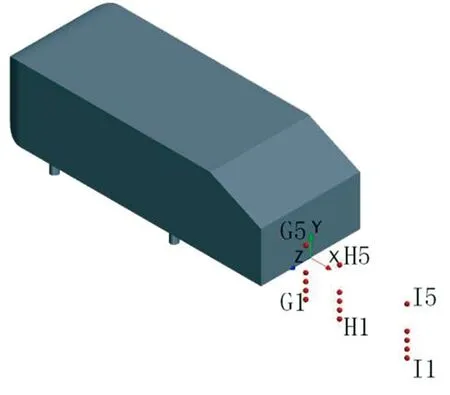
(a) 监测点分布(z*为0.52)

(b) G1～G5(x*为0.46)功率谱密度

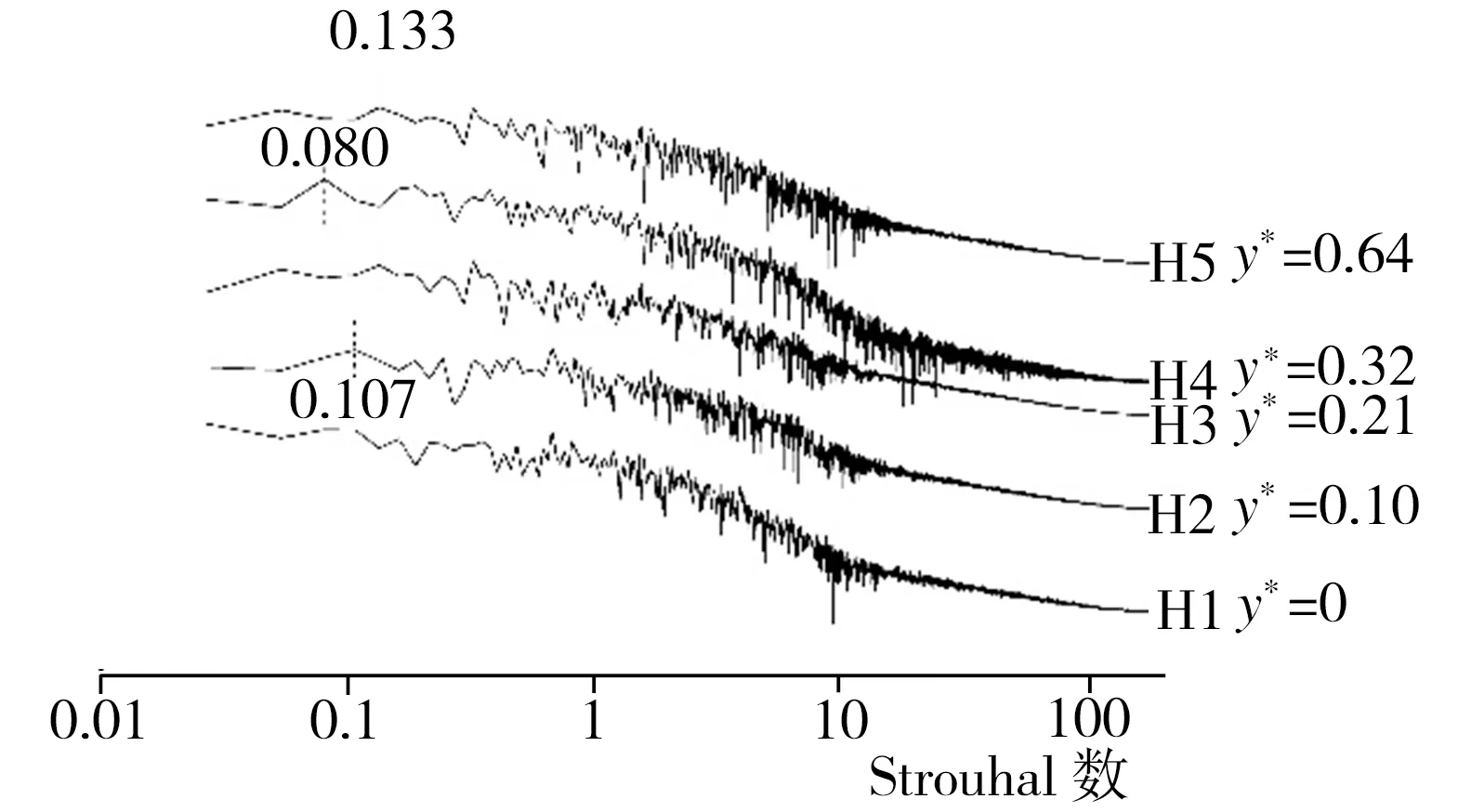
(c) H1～H5(x*为0.92)功率谱密度

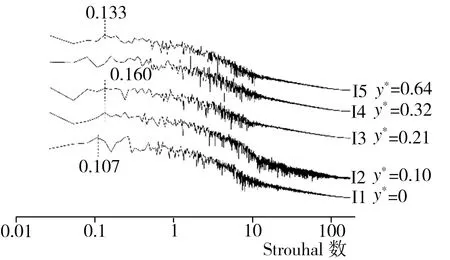
(d) I1～I5(x*为1.84)功率谱密度

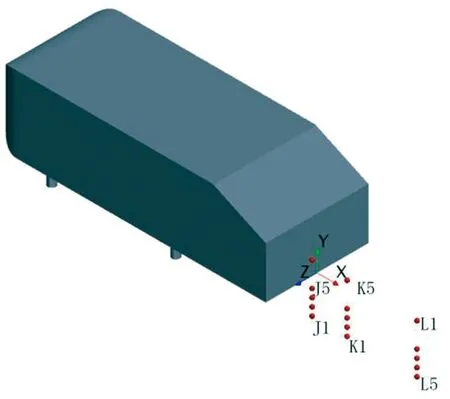
(e) 监测点分布(z*为0.67)

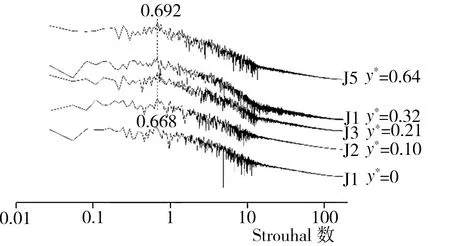
(f) J1～J5(x*为0.46)功率谱密度

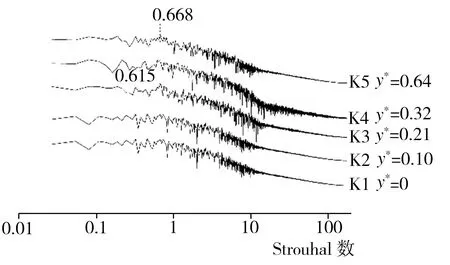
(g) K1～K5(x*为0.92)功率谱密度

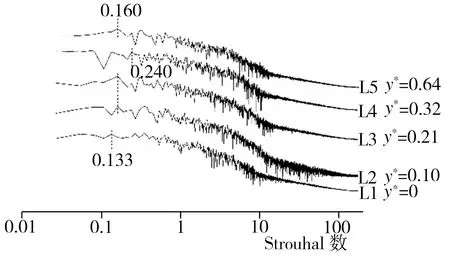
(h) L1～L5(x*为1.84)功率谱密度

2.2.3 模型尾迹区域底部流场的非定常特性

在模型尾迹区域y*为0的xoz水平面上布置M1～M6(x*均为0.10)6个监测点，监测点按序号1～6所对应的z*值依次为0.42、0.58、0.76、0.84、0.92，其具体布置情况以及根据模拟期间第13～23 s所收集流场流向速度信息做出的各监测点处流场功率谱密度曲线如图10所示。由图10可知，模型尾迹区域底部存在两种主要的涡系结构，第一种涡系结构特征峰的St为0.294，主要分布在z*分别为0.58、0.76、0.84、0.88的M2、M3、M4及M5处，第二种涡系结构特征峰的St为0.668，主要分布在M6(z*为0.92)处，这与文献[5]的研究结果类似，据该文献报道，在Re为0.62×105的条件下进行风洞试验并借助PIV技术分析模型尾迹区域流场时，发现该区域底部与本研究位置相似处也出现了两个典型特征峰，相应St分别1.76、2.11。本研究中M2～M5处出现的涡系结构(特征峰St为0.294)可能是因模型底部来流被模型支撑阻碍后形成了类似卡门涡街的涡脱落所致，而M6处出现的涡系结构(特征峰St为0.668)应该是模型侧面来流在模型底面与模型下方地板之间位置产生的一种侧向间隙涡。

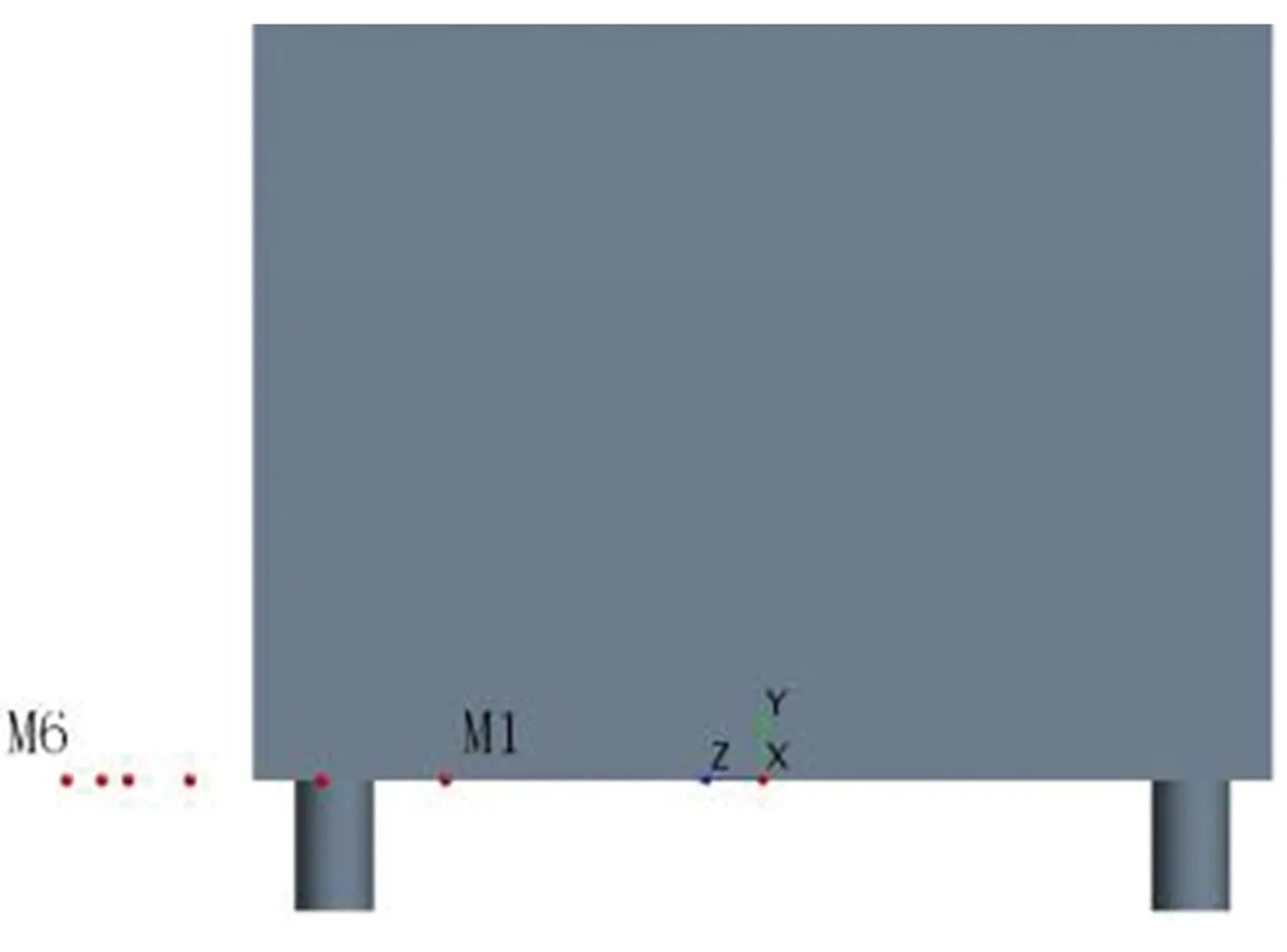
(a)监测点分布

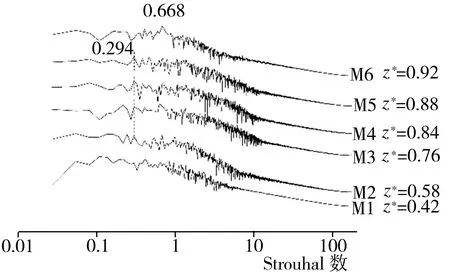
(b)M1～M6(x*为0.10)功率谱密度

2.3 Ahmed模型外部绕流流场拓扑结构

通过对Ahmed类车体模型尾部区域流场进行频谱分析，基本明确了该区域主要涡团的位置与特性，为了深入了解相关涡系结构之间的联系及演化过程，还需对类车体模型非尾部区域流场结构展开研究。首先，在类车体模型车顶y*为1.1的水平面上布置O1～O6(x*均为-2.71)、P1～P6(x*均为-1.48)、Q1～Q6(x*均为-1.04)3横排共计18个监测点，每排监测点按序号1～6所对应的z*值依次为0、0.16、0.26、0.34、0.42及0.67，监测点具体布置情况以及根据模拟期间第13～23 s所收集流场流向速度信息做出的各监测点处流场功率谱密度曲线如图11所示。由图11可知，在类车体模型车身上方y*为1.1的水平面上存在两种主要的功率谱密度特征峰对应该处的典型涡结构，相应峰值St分别为0.107和0.214，具体到O系列监测点(x*为-2.71)(图11(b))，在O1(z*为0)、O3(z*为0.26)处并未发现明显特征峰，在O2(z*为0.16)处则出现了St为0.107的特征峰，而O4(z*为0.34)、O5(z*为0.42)及O6(z*为0.67)处虽监测到特征峰的存在，但该峰St已变为0.214。至于x*为-1.48的P系列6个监测点，不仅全部出现了St为0.214的特征峰，而且在P4(z*为0.34)与P5(z*为0.42)处还存在St为0.107的特征峰。此外，在最靠近模型尾部倾斜表面边缘的Q系列监测点(x*为-1.04)中，Q4(z*为0.34)、Q5(z*为0.42)、Q6(z*为0.67)处均出现了St为0.107的特征峰，同时，在Q4和Q1(z*为0)处仍存在St为0.214的特征峰。结合2.2.1节分析结果可知，在类车体模型车身及尾部倾斜表面上方均出现了St为0.107的功率谱密度特征峰，这表明在类车体模型前端上方形成的涡结构对于车顶以及车尾倾斜面区域上方的流场分离具有显著影响，而St为0.214则是顶部涡功率谱密度最显著的特征峰值，在靠近车尾的Q系列监测点处，该峰的分布点已明显减少，表明顶部涡在此区域已近乎消散。其次，再讨论类车体模型车身侧面来流对模型尾迹区域流场的影响。在z*为0.74且与中截面xoy平行的纵截面上布置R1～R6(x*均为-2.71)、S1～S6(x*均为-1.48)两竖排共计12个监测点，每排监测点按序号1～6所对应的y*值依次为0、0.16、0.42、0.63、0.73、0.92，监测点具体布置情况以及根据模拟期间第13～23 s所收集流场流向速度信息做出的各监测点处流场功率谱密度曲线如图12所示。由图12可知，在此纵截面上主要存在两种不同的功率谱密度特征峰，其中一种St为0.668的峰出现在靠近地面位置的R1、S1、R2、S2处，另一种St为1.257的特征峰出现在位于车身中上部的R4、R5、R6及靠近车尾的S3、S4、S5、S6处，在与S3高度相同的R3处并未检测到该峰，由此推断St为1.257的特征峰对应于因模型侧面偏上方位置来流卷曲而形成的侧向涡，而在靠近地面处出现的St为0.668的特征峰则与尾迹区域出现的对应相同St的涡系结构(见2.2.2及2.2.3节)存在关联，该尾迹区域涡系结构的演化过程应为：类车体模型侧面偏下方的来流在车体与地板间隙处形成了间隙涡，间隙涡到达模型尾迹区域后在压差作用下上洗并向中面卷曲。最后，基于Ahmed模型周边不同涡系结构的频谱分析、分布状况及内在关联，推导出较低Re(1.48×104)条件下Ahmed模型外部绕流流场拓扑结构示意图如图13所示。

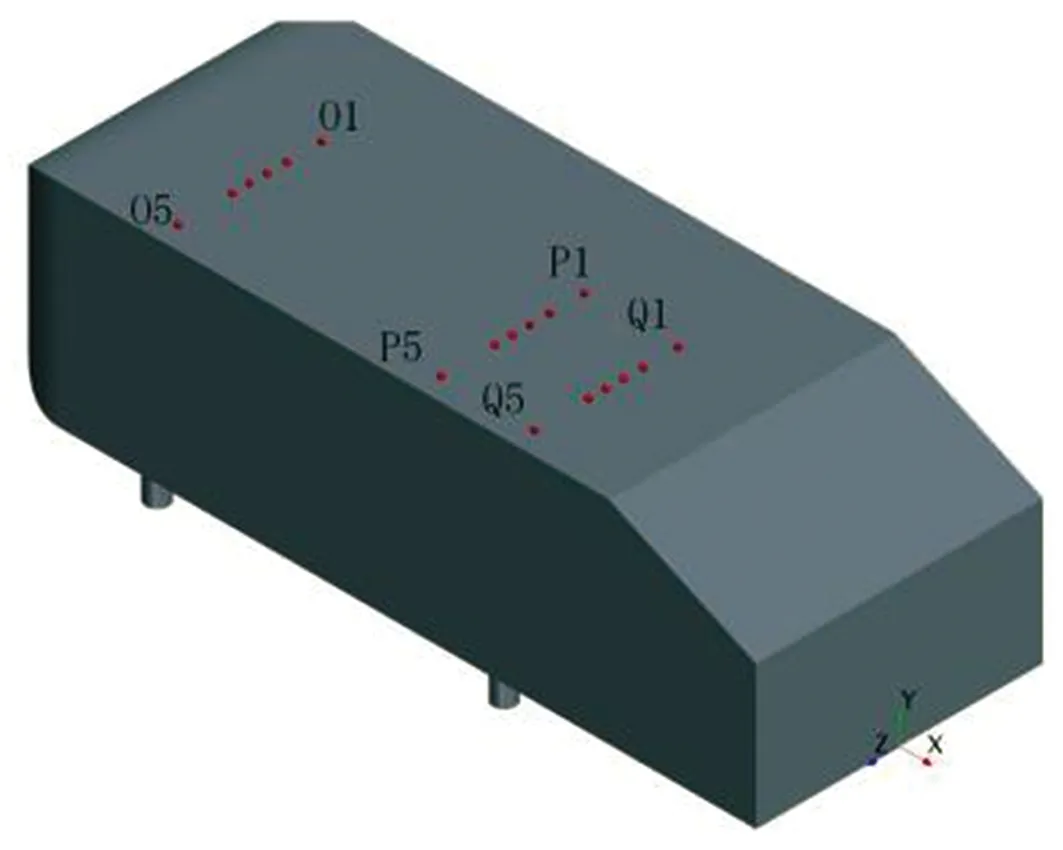
(a) 监测点分布

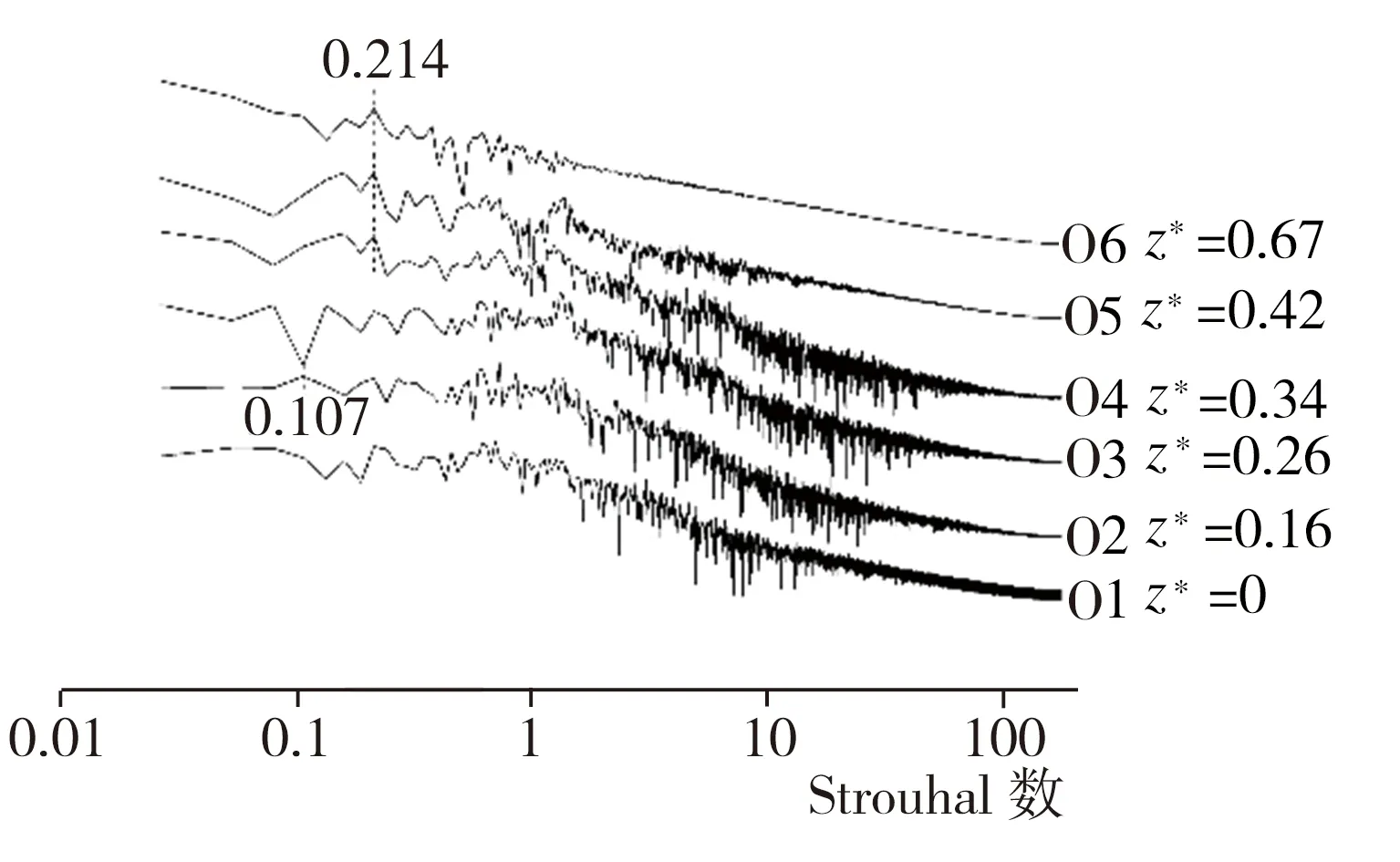
(b) O1～O6(x*为-2.71)功率谱密度

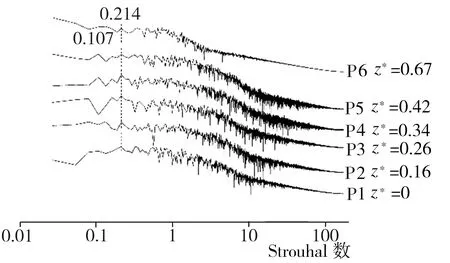
(c) P1～P5(x*为-1.48)功率谱密度

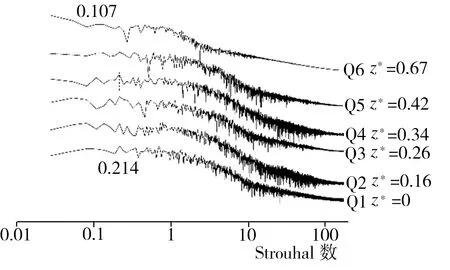
(d) Q1～Q5(x*为-1.04)功率谱密度

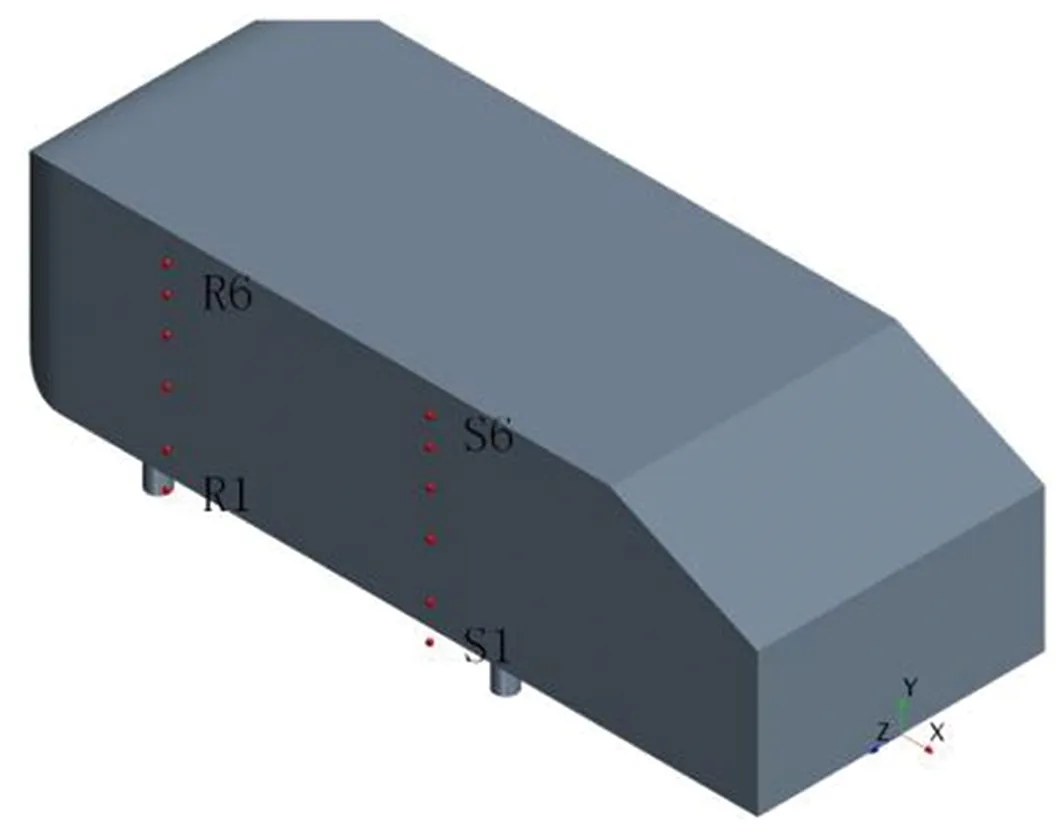
(a)监测点分布

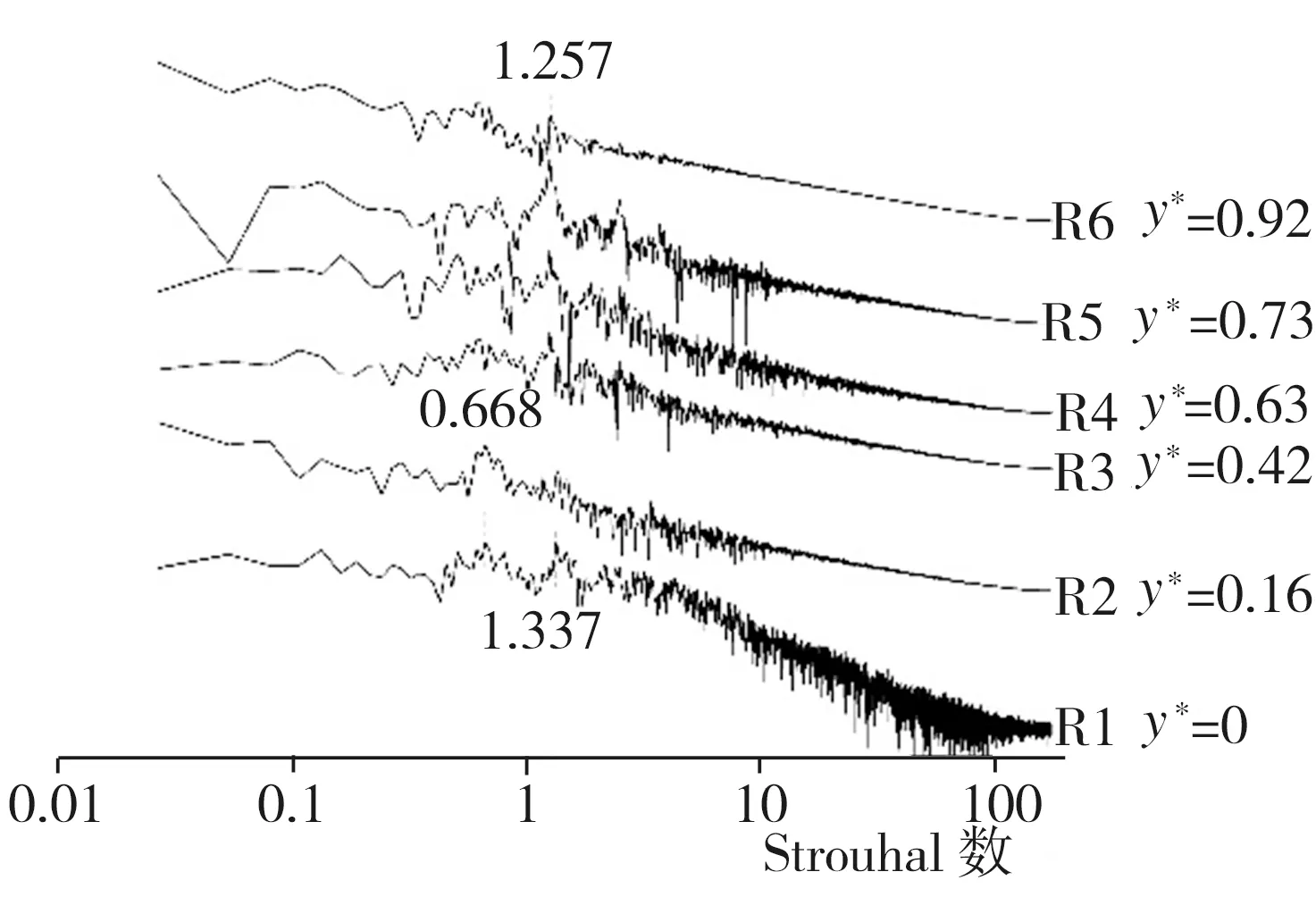
(b) R1～R6(x*为-2.71)功率谱密度

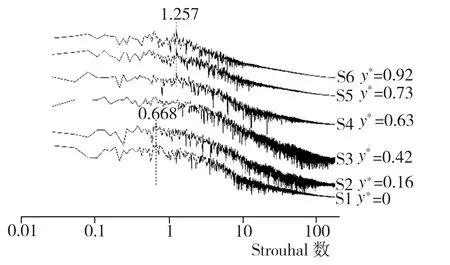
(c) S1～S6(x*为-1.48)功率谱密度

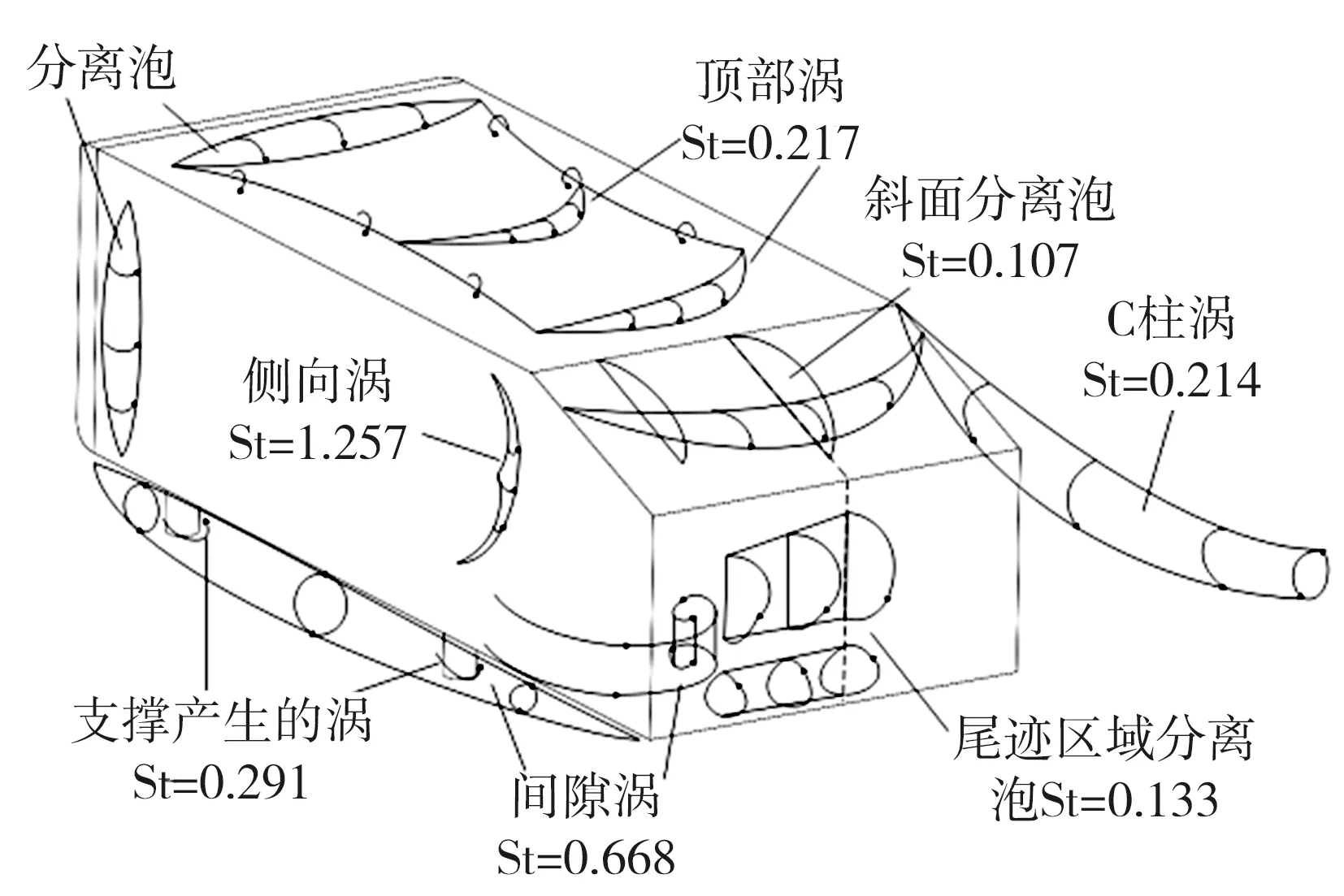
图13 外部流场拓扑结构

3 结语

车辆行驶过程中所受气动阻力对车辆油耗影响较大，而气动阻力主要来自汽车尾部并与尾部流场密切相关，为了明确尾部流场结构的特点与演化规律，本文基于低雷诺数下Ahmed模型的水洞实验，采用大涡模拟方法，先根据模型尾部区域流场时均流线轨迹来确定该区域的涡结构分布状况并于相应位置布置监测点，再借助频谱分析获取监测点处涡结构的特征值，然后结合模型非尾部区域的流场非定常特性追溯尾部涡结构的演化机理并绘制出Ahmed模型绕流流场的拓扑结构。分析结果表明，当来流经过Ahmed模型前端时会发生分离，并于模型前端上方与侧面发生卷曲分别形成顶部涡与侧向涡。在来流向下游即模型尾部继续流动的过程中，顶部涡强度逐渐减弱，基本消散于模型顶面与尾部倾斜表面交界处，与此同时，一部分顶部来流在模型尾部倾斜表面上方分离，并于该表面中部上方形成分离泡，另一部分顶部来流则与侧面来流在模型尾部倾斜表面两侧形成C柱涡。模型尾部倾斜面上的下洗流与模型底部上洗流在尾迹中心区域相互作用从而形成了分布范围较广的分离泡。此外，模型前端下方来流与侧面偏下方来流也在模型尾迹区域底部附近分别形成了底部与侧向间隙涡。