求解带序列相关准备时间双边装配线平衡问题的改进模拟退火算法

赵瀚明，唐秋华，蒙 凯，李梓响，张子凯

(1.武汉科技大学冶金装备及其控制教育部重点实验室，湖北 武汉，430081;2.武汉科技大学机械传动与制造工程湖北省重点实验室，湖北 武汉，430081)

在现代化生产中，装配线已经成为制造过程的核心和终端环节。根据布局的不同，装配线可分为单边装配线、双边装配线和U型装配线等。与传统的单边装配线相比，双边装配线在整线长度、物料搬运成本、设备利用率等方面具有明显优势[1]，因而在汽车等大型产品的制造过程中得到广泛应用。

双边装配线平衡是将装配任务依次分到装配线两边的各工位中，以实现成对工位数最少、总工位数最少、生产效率更高、负载更均衡等目标[2]。由于工艺流程的限制，装配任务之间存在优先关系约束，每个任务须等待其前序任务全部完成后才能开始。特别地，一个任务需等待同一成对工位内对面工位中的前序任务完成之后才能开始，这种情况下产生的等待时间称为与序列相关的空闲时间[3]。此外，装配线上的物料搬运、工件更换、模具准备等因素会导致机床需要额外的准备时间去执行某个既定任务，这种准备时间可分为与序列无关和与序列相关两种，前者时长固定，后者时长取决于同一工位内前后两个加工任务的工艺要求[4]。序列相关空闲时间和序列相关准备时间这两者都会对双边装配线造成一定影响，在双边装配线平衡时合理规划任务分配和任务序列，可以增加任务执行的并行度，提高生产效率[5]。

双边装配线平衡属于NP难问题[6],现有求解方法有精确算法[7]、群智能算法[8-10]和局部优化算法[11-12]。精确算法能找到问题的最优解，但计算时间很长，不适合在大规模和超大规模问题上使用。群智能算法鲁棒性强，受问题维数影响较小，具有较高的运行效率，但算法易陷入局部最优，收敛速度慢且优化性能受参数设置影响较大。与群智能算法相比，局部优化算法更关注问题特征，运算更快捷，所用参数更少[13]。模拟退火(Simulated Annealing，SA)算法是一种应用较广的局部优化算法，根据双边装配线平衡问题的特点对SA算法进行改进，能有效提升算法性能，实现全局搜索和局部搜索的均衡，更快找到性能更稳定的解。

Özcan等[14]首次提出带序列相关准备时间的双边装配线平衡问题(Two-sided Assembly Line Balancing Problem with Sequence-dependent Setup Times，TALBPS)，并设计了混合整数规划模型和启发式规则。Delice[15]采用融合10种启发式规则的遗传算法求解此问题。上述研究虽然考虑了序列相关准备时间和双边装配线平衡的集成，但在大规模算例上的搜索性能略显不足。Li等[16]证明以序列相关空闲时间最小化作为二级目标，能实现对大规模双边装配线问题的深度搜索。

为此，本文提出一种改进的模拟退火算法，用来求解带序列相关准备时间的第I类(最小化工位数)双边装配线平衡问题，以序列相关空闲时间为二级目标，并设计了基于分级位置权重的启发式初始化策略和改进的收敛准则，最后通过双边装配线标杆案例尤其是大规模案例,对算法的合理性和有效性进行实验验证。

1 问题描述

第I类双边装配线平衡问题最常见的优化目标是同时最小化成对工位数和总工位数[13]，即：

minf1(X)=wnm·nm+wns·ns

(1)

式中：nm和ns分别是分配完成后的成对工位数量和总工位数量；ωnm和ωns为参数，在双边装配线中，一般2个工位组成一个成对工位，因此参数ωnm和ωns的值分别设为2和1。

双边装配线平衡需要满足多种约束：节拍约束、方向约束和优先关系约束，并将加工任务按照一定的序列依次分配到各个成对工位上。图1所示为一个小规模案例的任务优先关系，图中包含12个任务，圆圈内的数字表示任务的编号；箭头指向表示任务之间的优先关系，由前序加工指向后序加工；括号内的数字表示任务的加工时间，文字表示任务的方向，其中，左/右表示任务必须分配到成对工位的左/右边，任意表示可分配到任意一边。

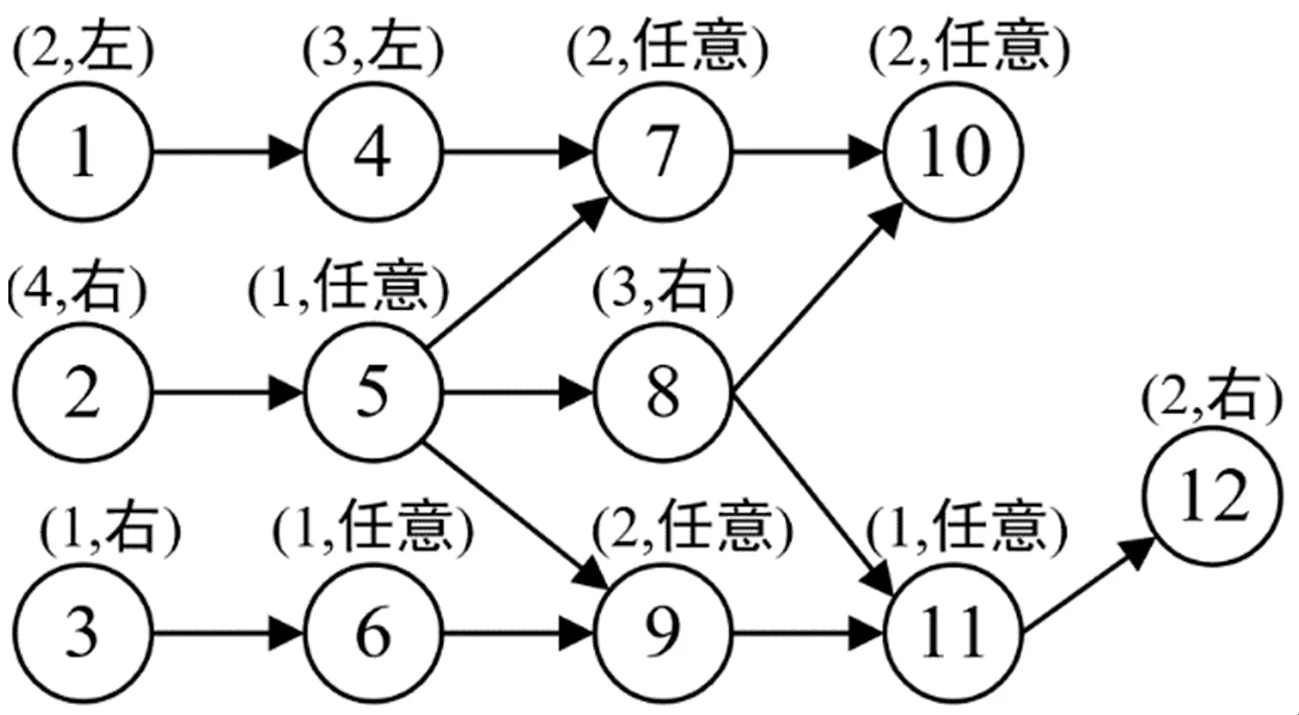
图1 12个任务的优先关系

在双边装配线上，由于优先关系的约束，工位中会产生与序列相关的空闲时间。此外，在同一工位内执行两个连续的装配任务时，还会产生序列相关的准备时间，在以前的文献中大多忽略了此准备时间[4]。在实际生产中，当准备时间比空闲时间短时，可以将其包含在空闲时间内，此时确实可以忽略准备时间对装配线的影响;然而当准备时间比空闲时间长时，准备时间包含在空闲时间内会导致后续加工任务延后。针对图1所示案例，图2(a)和图2(b)展示了装配线节拍为5时不考虑准备时间与考虑准备时间的两种任务分配结果。图2(b)中，任务1、5和任务3、7之间，准备时间比空闲时间短；任务9、11之间，准备时间比空闲时间长。从图中可以看出，考虑序列相关准备时间时所需要的成对工位数和总工位数均多一个。由此可知，序列相关准备时间对生产效率具有显著影响，在装配线平衡时不能将其忽略。

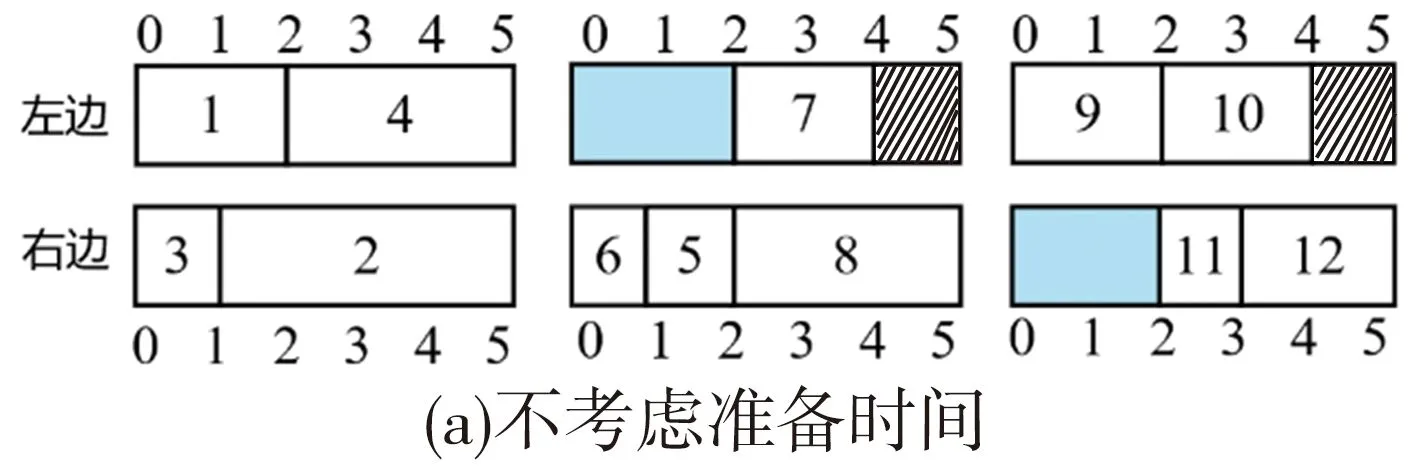
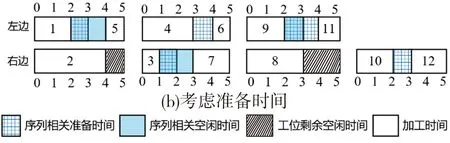
图2 考虑准备时间与不考虑准备时间时的任务分配

2 改进的模拟退火算法

2.1 编码及解码

针对双边装配线平衡问题的编码，目前主要有基于任务序列、基于工位和基于分区等6种方式。Li等[13]测试了所有的编码方式，认为基于任务序列的编码是最优方案，故本文采用此方式进行编码，即根据任务之间的优先关系，按照实数编码生成初始解。例如，对于图1所示的优先关系，可生成一个初始解：{3, 2, 1, 5, 4, 8, 6, 7, 9, 10, 11, 12}。

关于解码，目前存在着任务-工位和工位-任务等10种解码方式，本文采用文献[13]所证明的最优解码方式ST5，即优先选择当前工位余量更大的边进行分配，余量相同则选择左边，再根据任务优先策略选择可优先分配的任务进行分配。而针对TALBPS问题，还要对ST5中的任务优先策略进行调整，在选择可优先分配的任务时需要额外限制考虑准备时间后的任务总时长仍然在节拍内。

2.2 基于分级位置权重的初始化

原始的模拟退火算法采用的是随机初始化，随机性导致初始解的质量较差，需要进行改善。分级位置权重(Ranked Positional Weight，RPW)是装配线平衡领域中性能较优的启发式初始化方法，具有提升工位平均负荷、降低装配平衡延迟率和生产线平滑性指数等优势[5]。每个任务的位置权重等于其加工时长与所有后序任务的加工时长的总和，具体计算步骤为：

(1)根据优先关系找出每个任务的全部后序任务。

(2)按照下式计算每个任务i的RPW权值。

(2)

式中：n为最大任务数；ti为任务i的加工时间；当任务j是任务i的后序时，δij=1，否则δij=0。

(3)按照RPW值从大到小排序，生成初始解。

位置权重越大的任务意味着其后序任务总时长越大，优先分配可使得其后序任务尽早开始，从而减少在制品堆积，使得各工位工时分配接近满载。这样就有可能减少装配线上序列相关的空闲时间，总的工位数量也可能减小。

2.3 改进的收敛准则

模拟退火算法是基于迭代求解策略的一种随机寻优算法，其基本原理是由当前解通过邻域搜索产生一个新解，并采用Metropolis准则决定是否接受这个解。以式(1)中的目标作为适应度值，计算出SA算法的原始Metropolis收敛准则为

(3)

式中：df1=f1(X2)-f1(X1)，其中f1(X1)为当前解的适应度值，f1(X2)为新解的适应度值；T为温度控制参数，T=T0q，其中T0为较大的初始值，q为衰减系数，一般取值为0.8～0.99。

式(3)表示：当新解比当前解更优(df1<0)时，采用新解替换当前解；否则，按照一定的概率接受恶化解，且概率exp(-df1/T)的值随着温度递减而逐渐减小。Metropolis准则对新解的收敛方向直接决定了SA算法的搜索性能。

然而对于双边装配线平衡问题，由于方向约束、优先关系约束等限制条件的复杂性，当算法迭代到一定次数后，得出的解的适应度值f1(X)往往相同[13]，难以区分出性能更优的解。此时若采用SA算法原始的Metropolis准则，接受新解的概率很低，算法容易陷入局部最优，因此本文提出改进的Metropolis收敛准则，见式(4)。

(4)

式中：df2=f2(X2)-f2(X1)，其中f2(X)为工位空闲时间函数，计算公式为：

f2(X)=

(5)

式中：J为成对工位集；CT为装配线节拍；j和k分别代表成对工位和方向；STjk为分配到工位(j,k)上的任务时间，故CT-STjk为工位(j,k)上的空闲时间。

从式(4)可以看出，改进Metropolis收敛准则对解的性能作了进一步的区分，并按照不同的概率接受性能不同的解。针对TALBPS-I问题，改进收敛准则中的工位空闲时间函数f2(X)赋予越靠前的成对工位上序列相关的空闲时间越大的权重，在一级目标f1(X)相同的情况下，二级目标f2(X)越小意味着前面的成对工位负载更饱满。在算法迭代过程中尤其是迭代后期，当df1=0、df2<0时，按照概率1接受新解。此外，改进的收敛准则又区分了工位数量更大(df1>0)和工位数量相同、工位空闲时间更长(df1=0、df2≥0)两种不同劣解的情况，分别以概率exp(-df1/T)和略小于前者的概率exp(-df2/T)来接受劣解，增大了跳出局部极值的可能性。

2.4 改进的模拟退火算法流程

融合上述算子设计的改进SA算法流程见图3。首先，采用基于分级位置权重的启发式初始化

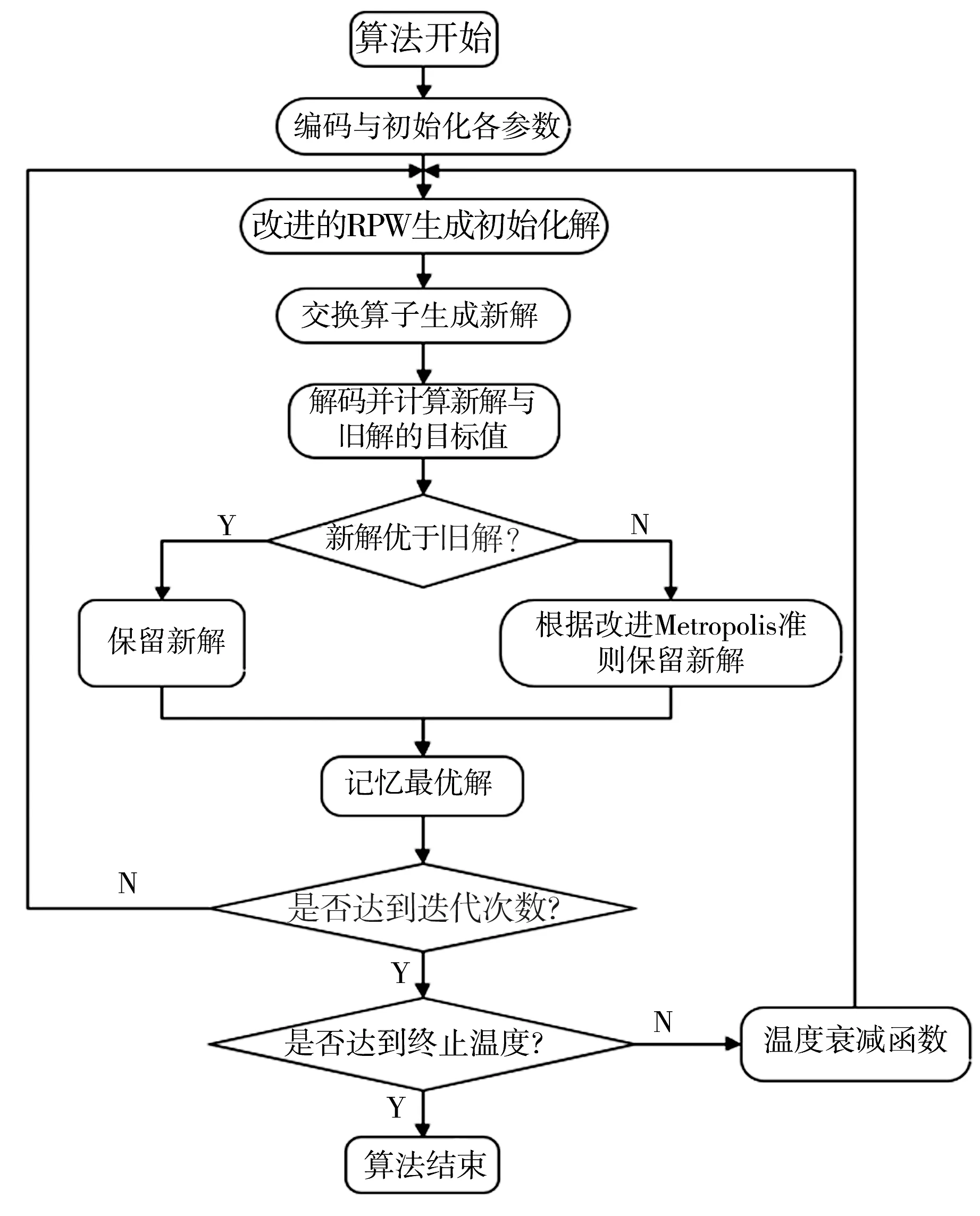
图3 改进模拟退火算法的基本流程

策略，并进行局部搜索使用交换算子产生新解；然后，通过解码得出新解与旧解的适应度值，并执行改进的Metropolis收敛准则，保留性能最优的解，通过一定的概率接受性能较差的解；最后通过温度衰减直至达到终止条件。

3 实验结果与分析

算法采用MATLAB语言编程，所有实验都在Intel(R) Core(TM) i5-9300H CPU 2.40 GHz 7.79 GB RMA个人电脑上使用Microsoft Windows10系统进行测试。为了保证算法对比的公平性，采用Ni×Ni×ρms作为终止条件，其中Ni为测试案例的任务数量，ρ一般取值5、10、15等。这个公式保证了算法运行时间随着问题规模的增大而增大，对不同规模案例的计算有了相对一致的终止准则。每次实验的性能通过相对百分比偏差(Relative Percentage Deviation，RPD)来衡量[16]。

(6)

式中：Somesol和Best分别为任意一种参数组合获得的工位数量和所有参数组合获得的最优工位数量。RPD值越低意味着算法的性能越好。

3.1 算法参数校验

参数设置对算法性能影响很大，故需要进行参数校验。对于SA算法，有4个可调整的控制参数：初始温度T0、结束温度Tend、降温速率q、每个温度下的迭代链长L。每个参数设置3个水平：T0∈{500，1000，1500}，Tend∈{0.01，0.1，1}，q∈{0.9，0.95，0.98}，L∈{50，100，150}。设计4因素3水平的正交实验，共有27种参数组合。考虑到大规模案例的参数对中小规模案例同样有效，故求解最复杂的大规模标杆案例P205[10]并取最大节拍2832，以运行时间Ni×Ni×5 ms为终止条件，每个实验运行5次。以5次实验中的最小RPD作为最终响应值，对所有实验组合采用田口分析法，信噪比(SNR)均值越大表示该参数水平性能越好[17]。实验结果如图4所示，最佳参数组合为{T0=500，Tend=0.1，q=0.9，L=100}。为了保证实验的公平性，以上方法也用于后文中进行对比的其他智能算法的参数校验。

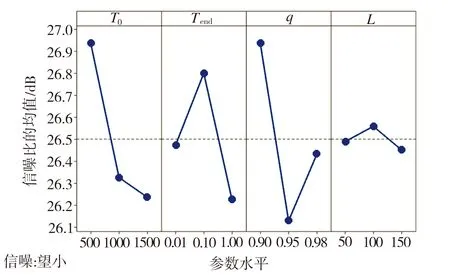
图4 模拟退火算法参数的信噪比主效应图

3.2 改进算子性能测试

与原始SA算法相比，本文算法提出了两点改进：基于分级位置权重的初始化以及改进的收敛准则。为了验证两点改进策略的有效性，将原始SA算法、只加入基于分级位置权重初始化策略的SA算法(SA_RPW)、只加入改进的收敛准则的SA算法(SA_Met)和本文改进SA算法进行对比实验。

为保证改进策略的普适性，分别对大规模案例P65[10]、P148[1]和P205[10]进行求解，由于每个案例设置有不同的节拍，故一共有22个案例。以运行时间Ni×Ni×5 ms为终止条件，每个实验运行5次，取最小RPD值和平均RPD值进行分析。采用方差分析对4种算法的所有结果进行统计，得到RPD值的95%置信区间，如图5所示。由图5可以看出，SA_RPW和SA_Met两种算法求得的RPD值都要比原始SA求得的RPD值小，证明所提出的两点改进策略都是有效的。同时，本文SA算法性能最佳，这是因为两种改进策略之间存在较强的互补性：分级位置权重减少了整条装配线上序列相关的空闲时间，使得各工位尽量以满负荷进行生产作业，达成工位数量最小化的目标；改进收敛准则使序列相关空闲时间向后面的成对工位集中，减少了所需的成对工位和总工位数量，促使解的性能更优，此外，改进收敛准则还进一步区分出解的性能，以不同概率接受劣解，避免算法陷入局部最优。

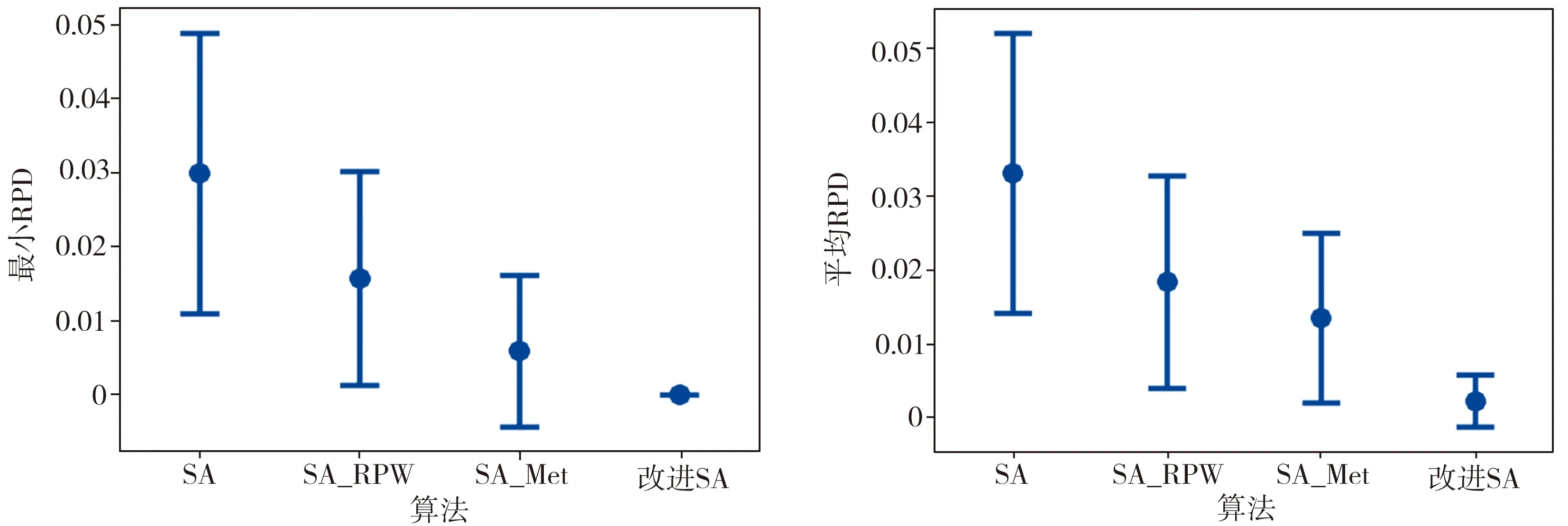
(a)最小RPD值

3.3 算法求解

为了分析准备时间对装配线上工位数量的影响，采用本文算法求解TALBPS标杆案例，包括4组小规模案例(P9[8]、P12[8]、P16[10]、P24[8])和3组大规模案例(P65[10]、P148[1]、P205[10])，其中P148案例的部分任务的加工时间按照文献[10]进行调整。每组案例设置有不同的节拍，总共有37个案例。为保证计算公平，每次计算以运行时间Ni×Ni×10 ms为终止条件，每个案例求解5次。此外，对两个水平的准备时间分别计算，低水平准备时间在区间U[0，0.25·min∀i∈ITi]内随机产生，高水平准备时间在区间U[0，0.75·min∀i∈ITi]内随机产生，其中，Ti为每个任务的加工时间，I为所有任务的集合。计算结果如表1所示，其中，NM[NS]表示5次结果中的最小成对工位数量和总工位数量，LB表示两种水平准备时间下理论上的最小工位数量[14]，BWS表示目前已知文献中标准双边装配线平衡问题标杆案例的

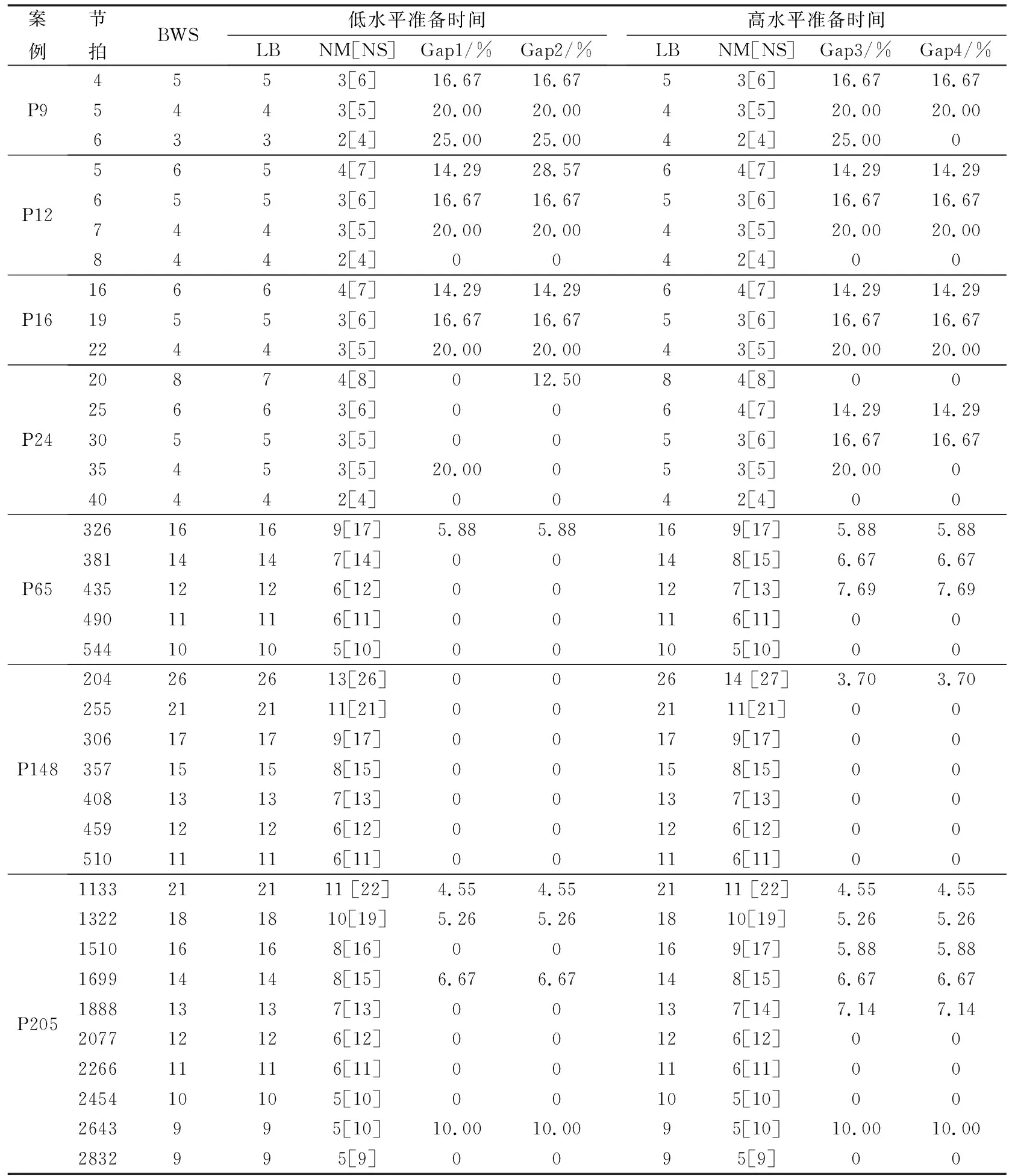
表1 标杆案例计算结果

最优解[18]，Gap1、Gap3和Gap2、Gap4分别表示两种水平准备时间下所求NS值与BWS和LB之间的相对百分比偏差。

从表1可知，在给定的运行时间内，本文改进SA算法均能求解出所有大规模标杆案例的结果，其中，低水平准备时间下的相对百分比偏差Gap1和Gap2的平均值分别为5.84%和6.02%，高水平准备时间下的相对百分比偏差Gap3和Gap4的平均值分别为7.51%和6.30%。而在文献[14]中，对应的结果与BWS之间的相对百分比偏差分别为Gap1=8.67%、Gap3=12.69%，在文献[15]中，对应的结果与LB之间的相对百分比偏差分别为Gap2=13.86%、Gap4=20.73%，这是笔者已知的现有文献取得的最优结果。相比较而言，本文提出的改进SA算法取得的结果明显更优。

3.4 算法对比

为了进一步验证本文算法的性能，将其与另外5种应用较多的典型算法进行了比较，包括遗传算法(Genetic Algorithm，GA)[15]、迭代贪婪算法(Iterated Greedy Algorithm，IG)[13]、变邻域搜索算法(Variable Neighborhood Search，VNS)[18]、禁忌搜索算法(Tabu Search，TS)[13]、粒子群算法(Partical Swarm Optimization，PSO)[13]，前面3种算法基于相应文献中的改进对它们进行了重新编码和调整，后面2种算法采用本文提出的两点改进策略进行了重新编码和调整。通过实验可知，这5种算法每次均能求得案例P148在表1中全部节拍下的最优解，故本节实验只针对大规模标杆案例P65和P205，其他实验条件与3.3节相同，表2所示为6种算法求得的最小RPD和平均RPD值。

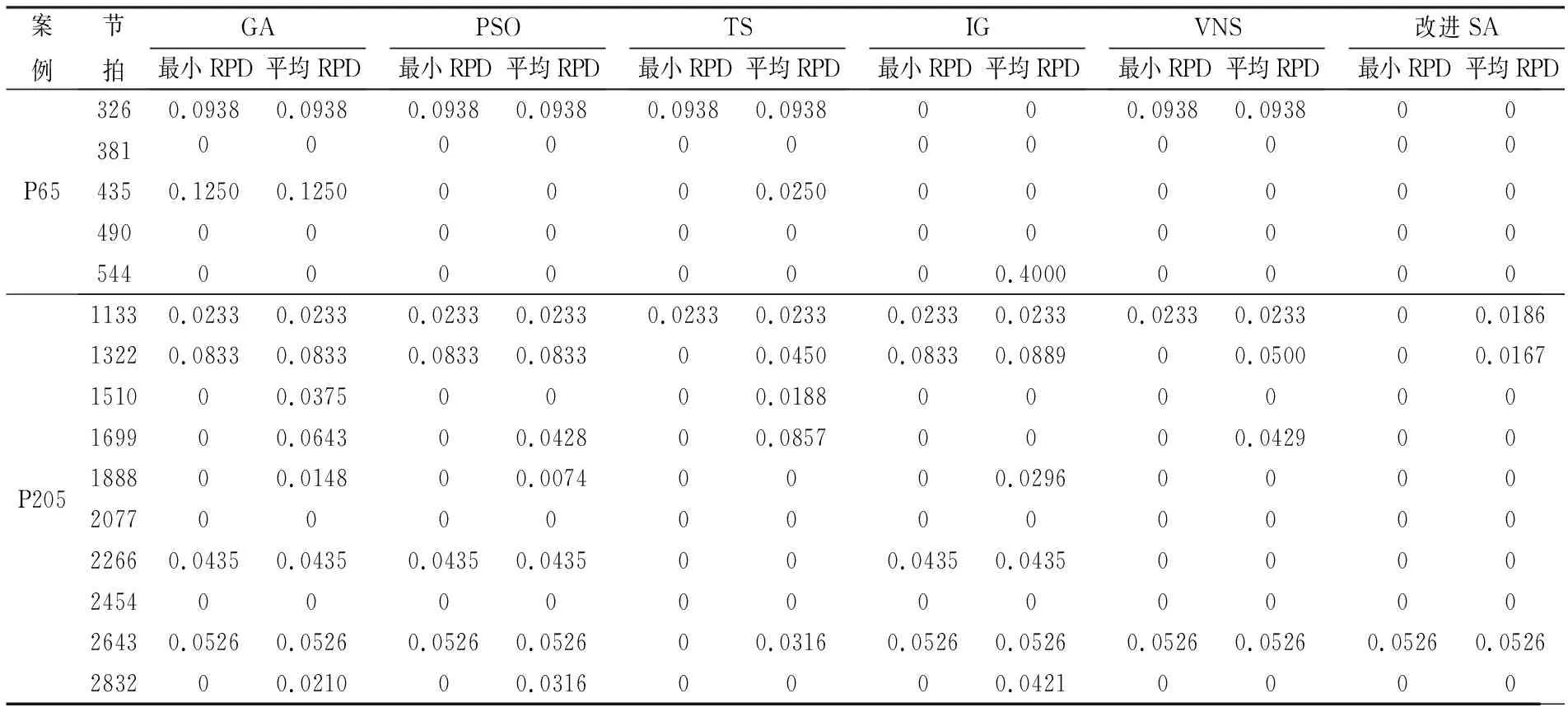
表2 改进SA算法与其他5种对比算法的性能比较

从表2可以看出，在相同的终止条件下，本文提出的改进SA算法几乎在所有案例中都表现出优于对比算法的性能。通过方差分析对6种算法的RPD值进行统计，结果如图6所示。由图可见，在95%置信区间上，改进SA算法的最小RPD和平均RPD这两个指标都要显著优于其他5种算法，并且局部优化算法IG、VNS和TS的性能略优于群智能算法PSO和GA，展现出改进的局部优化算法跳出局部最优而收敛于全局最优的能力，也印证了算法允许在一定程度上接受劣解的必要性。

(a)最小RPD

4 结语

本文针对带序列相关准备时间的第I类双边装配线平衡问题，提出了一种改进的模拟退火算法，其中包含两种不同的改进算子：基于分级位置权重的初始化策略以及改进的收敛准则。对比实验证明这两点改进是非常有效的，且两个改进策略之间存在一定的互补性，其综合应用性能最佳。应用本文算法求解不同规模的TALBPS标杆案例，计算结果与理论最小工位数目更为接近，优于已知文献中的最优结果。与其他5种典型算法(变邻域搜索算法、粒子群算法、遗传算法、迭代贪婪算法和禁忌搜索算法)相比，本文算法在最小相对百分比偏差和平均相对百分比偏差两个性能指标上显著更优。未来研究将考虑工位间需要准备时间情形下的双边装配线平衡、并行双边装配线平衡以及双边装配线平衡与预防维护的集成优化等问题。