液压伺服被动柔顺关节的柔顺特性分析

刘纯键，蒋 林,2，任利胜，潘孝越，周 玲，赵 慧,2

(1.武汉科技大学冶金装备及其控制教育部重点实验室，湖北 武汉，430081；2.武汉科技大学机器人与智能系统研究院，湖北 武汉，430081)

液压伺服柔顺关节作为液压机械臂类机器人的主要部件，具有输出力矩较大、传动平稳、结构简单、响应速度快以及精度高等特点，但因其负载刚度较大，当发生人机物理碰撞时，对人或设备所造成的伤害程度也更严重[1-3]。为了解决输出力矩较大的液压机械臂类机器人的人机物理接触安全性问题，需有效提升液压驱动机构在意外碰撞发生瞬间对碰撞及时做出反应的能力。已有研究表明，增强机器人关节柔顺性有助于化解或降低人机物理接触时的撞击力，其中机器人关节柔顺性又可分为被动柔顺性[4]和主动柔顺性[5]，前者指机器人藉由柔性机构在与外部环境接触时表现出的自然顺从，后者则是在力反馈作用下，机器人通过主动控制输出力而表现出的一种柔顺性。不过，产生力反馈需要一定的时间，而实际中人机碰撞的发生具有不确定性，并且作用时间通常很短暂，机器人关节主动柔顺性控制往往来不及发挥作用，伤害就已经造成，因此开发具有被动柔顺性的机器人关节就显得尤为重要。当前，随着智能材料和新型驱动技术的发展，被动柔顺关节虽已得到广泛应用[6-8]，但仍存在一些实际问题，例如张亚平等[9]在电机输出端面设置弹性环，通过弹性环的挤压变形实现了关节输出刚度可变，然而弹性环控制精度不足，难以满足传动平稳的要求；Wolf等[10]设计了具有双电机并联结构的柔顺关节，利用功率较小的电机即可调节关节输出刚度从而实现模拟人类行走步态的仿生控制，但双电机驱动无法支持较大力矩的输出；田柳滨等[11]通过在传统机器人关节的刚性结构内部嵌入磁流变传动机构，兼顾了其刚性与柔性,同时提出一种新型机器人柔顺关节设计理论并进行了运动学建模研究，但未利用相关的仿真实验对该理论进行验证。为了给柔顺关节设计提供新的思路，以拓展液压关节的功能性，本文设计了一种液压伺服被动柔顺关节并根据该关节基于液压伺服原理的数学模型构建相应的MATLAB/Simulink仿真模型，借助碰撞仿真实验研究了在意外碰撞发生瞬间液压伺服被动柔顺关节对碰撞进行处理的能力，从关节位置响应和柔顺度的角度对该关节的柔顺性进行了分析与验证。

1 液压伺服被动柔顺关节的结构与工作原理

液压伺服被动柔顺关节结构如图1所示，其主体由液压驱动机构及安装在液压驱动机构阀体输出轴上的力矩传递机构组成，其中液压驱动机构即液压转角自伺服柔顺随动机构是由先导级伺服阀柔顺驱动器改进而来，同时结合具有浮动位的大流量液压转角自伺服机理，采用阀芯穿过阀体与力矩传递盘连接的设计使该回转关节具有被动随动特性，通过机构整体运转实现关节在撞击发生时的随动控制[12]，而力矩传递机构则是实现液压伺服关节被动柔顺性的关键部件，该机构主要由托盘、支撑轮机构、力矩传递盘等组成(见图2)。当关节末端所受碰撞干扰力矩传至力矩传递机构且力矩大小超过阈值时，力矩传递机构将从高刚度模式转换为低刚度模式[13]，此时支撑轮机构连同力矩传递盘与连接阀体输出轴的托盘分离，之后力矩传递盘带动阀芯转动即阀芯相对阀体旋转，同时液压自伺服阀体输出轴也被动跟随阀芯运动，造成输出力矩减小，从而提高了人机物理碰撞的安全性。当碰撞干扰力矩撤销后，支撑轮机构将重新弹回至卡口，同时与其连接的力矩传递盘也带动阀芯恢复原状，使得液压关节输出力矩正常化，即碰撞干扰力矩撤销后液压关节又重返稳定状态。至于力矩传递机构的高、低刚度模式切换机制，则由其托盘的轮廓曲线方案(见图3)所决定，从图3所示的托盘轮廓曲线可以看出，轮廓曲线整体可分为高、低2种刚度区域并存在3个刚度转换点，其中处于正常工作模式下的高刚度区域即卡口位置，处于碰撞模式下的低刚度区域即斜坡位置，3个刚度转换点分别是非工作状态下支撑轮底部水平相切位置、达到触发被动柔顺性临界值时卡口轮廓与斜坡相接的位置以及到达斜坡最高点时支撑轮与垂直壁接触时的位置。通过分析、设计托盘轮廓，可实现液压关节在发生碰撞时从高刚度模式到低刚度模式的转换，从而提升其使用安全性，同时还能保证液压关节在正常工作模式下处于高刚度及快速响应状态。

(a)关节模型

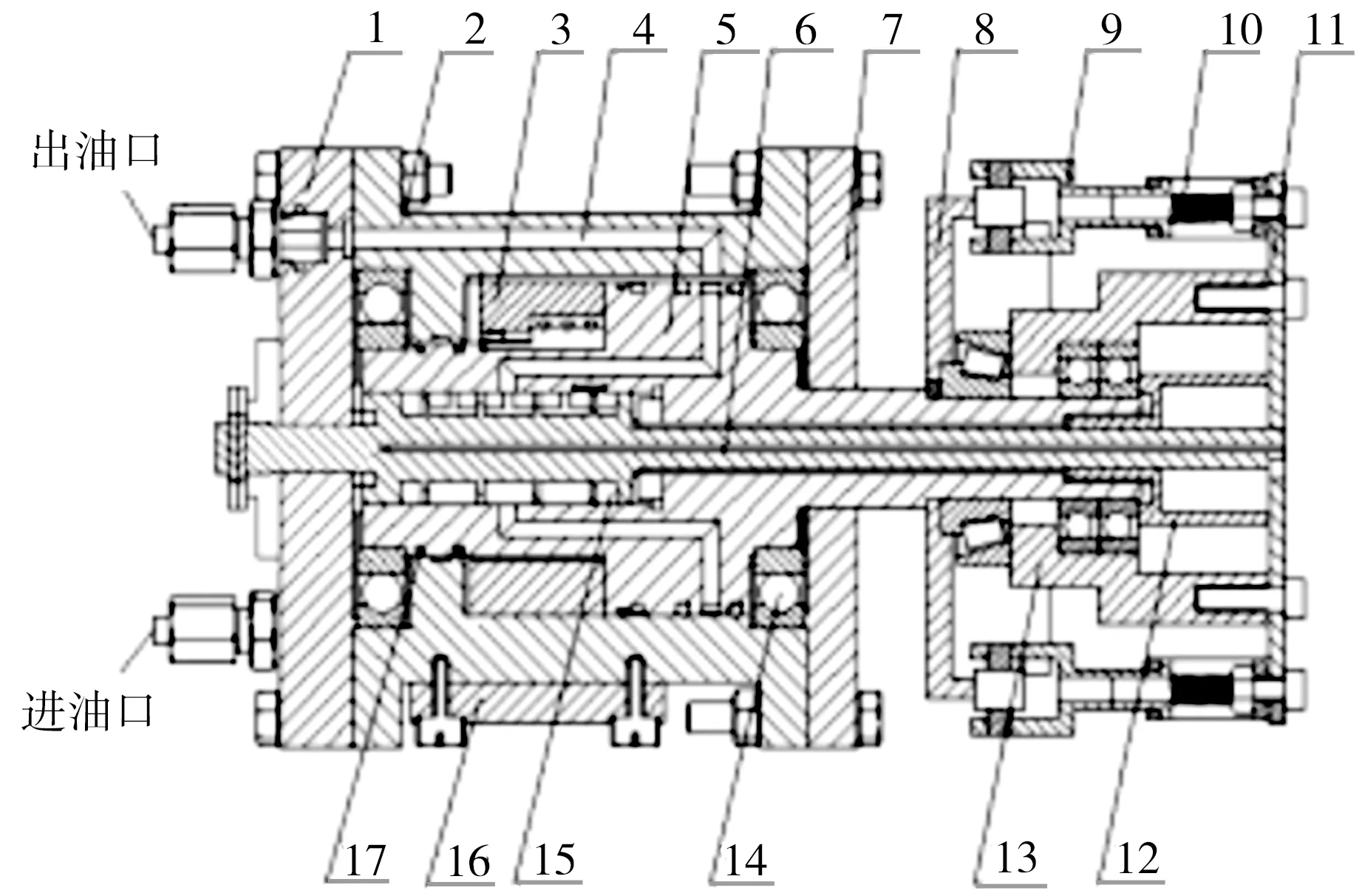
1—左端盖;2—缸体;3—叶片;4—低压油通道;5—阀体;6—阀芯;7—右端盖;8—托盘;9—支撑轮;10—弹簧;11—力矩传递盘;12—支撑套;13—定位套;14—深沟球轴承;15—阀套;16—固定挡块;17—密封圈(b)关节剖视图图1 液压伺服被动柔顺关节示意图

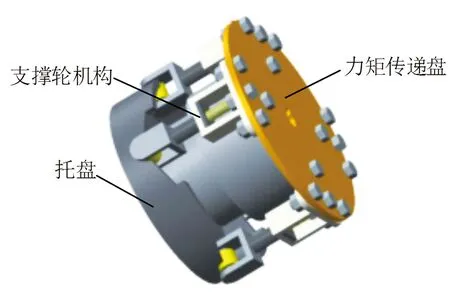
图2 力矩传递机构

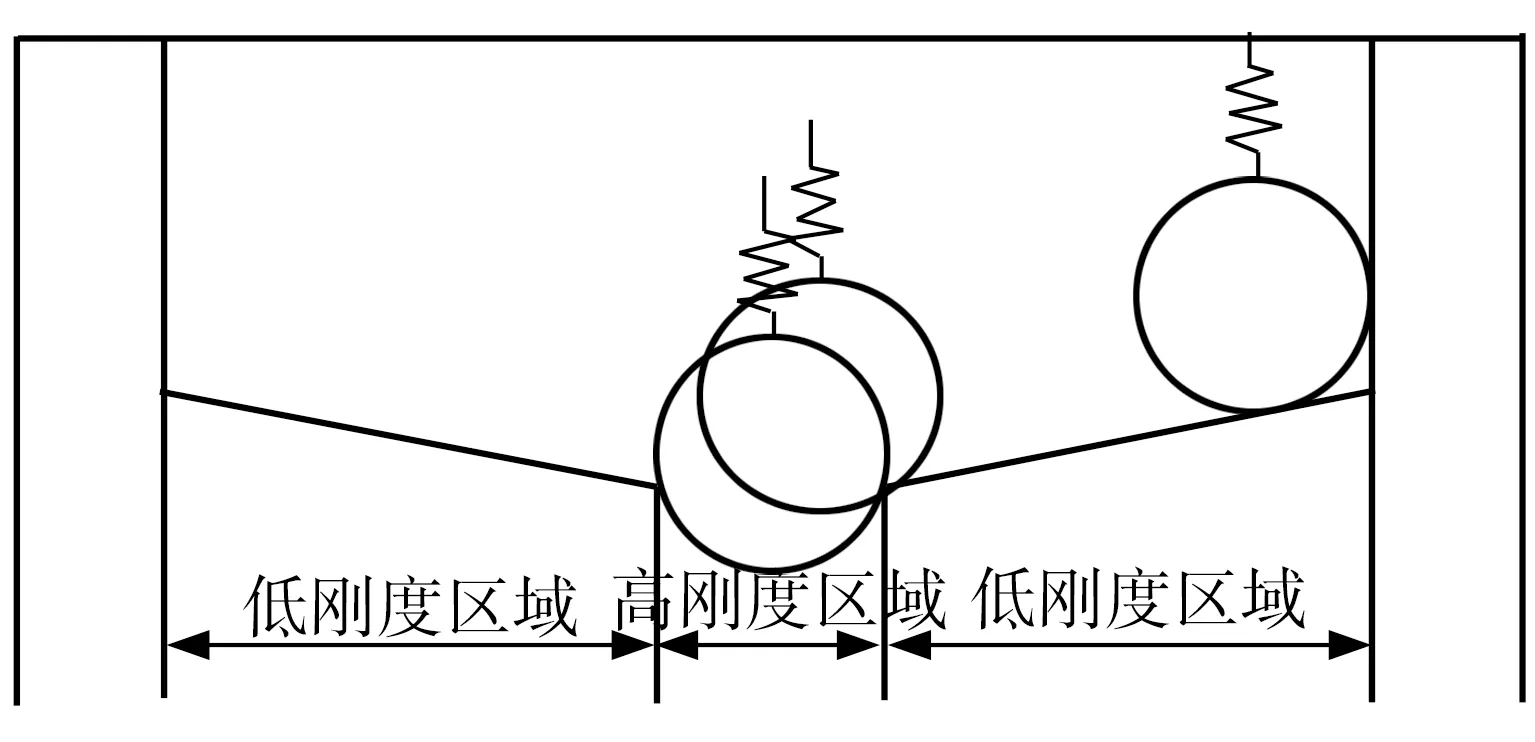
图3 托盘轮廓曲线

2 液压伺服被动柔顺关节的动力学模型

2.1 力矩传递机构的动力学模型

力矩传递机构是控制液压伺服关节被动柔顺性的主要部件，也是搭建关节数学模型的基础。当关节输出轴末端所受作用力传至力矩传递机构并超过阈值时，力矩传递机构的力矩传递盘将带动阀芯转动，其转动状态示意图如图4所示。

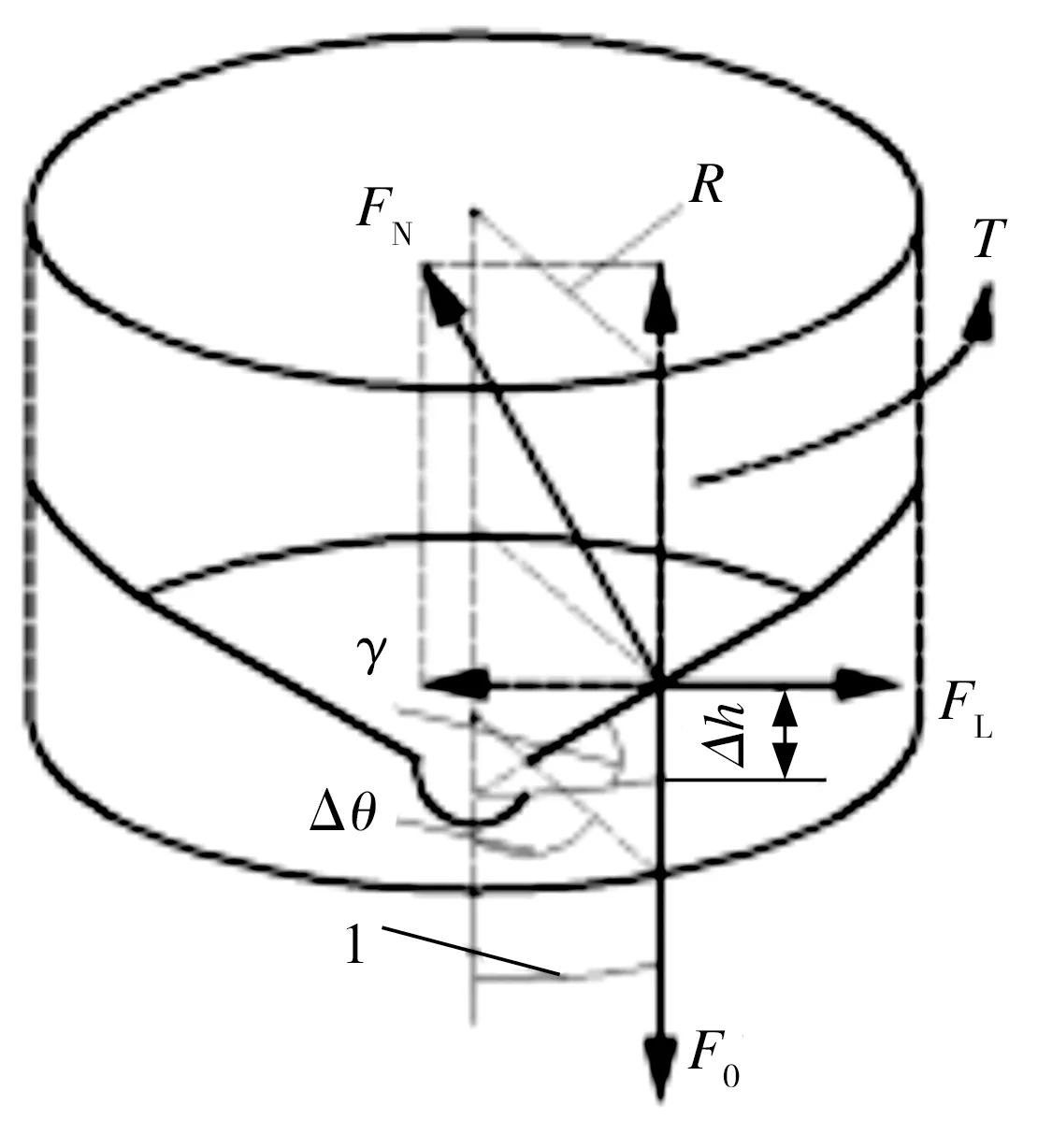
图4 力矩传递机构的转动状态

在图4中，力矩传递盘(半径为R)受碰撞干扰力矩T作用发生回转，阀芯回转角度为Δθ，托盘斜坡角度为γ，力矩传递盘转动弧线的长度为I。因本研究所设计的力矩传递机构中共有4个支撑轮，加之该机构结构紧凑，故可认为所有支撑轮受力均匀，对单个支撑轮进行受力分析，FN为托盘斜坡对支撑轮的支撑力，F′L为碰撞干扰力矩T折算到单个支撑轮上的外部作用力，F0为支撑轮机构中的弹簧弹力，弹簧压缩量为Δh。

根据图4，F′L、F0与FN之间存在如下关系：

(1)

设总的碰撞干扰力为FL，则有：

(2)

(3)

设支撑轮机构的弹簧刚度系数为k，则F0的计算公式为：

F0=Δhk

(4)

此外，图(4)中所示的几何量存在如下关系：

(5)

l=ΔθR

(6)

联立式(1)～式(6)，消除中间变量，最后可得阀芯回转角度Δθ为：

(7)

又因：

(8)

式中，kR为力矩传递机构的转动刚度，则有：

kR=4R2ktan2γ

(9)

基于式(9)，通过改变γ及k，对转动刚度kR进行数值仿真模拟，结果如图5所示。

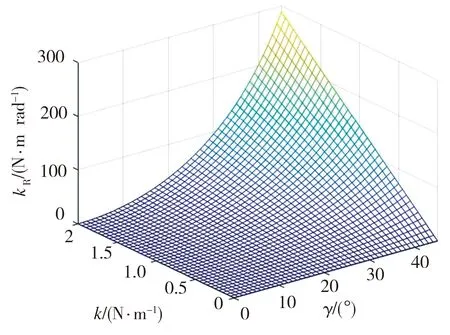
图5 转动刚度数值模拟结果

2.2 阀口流量方程

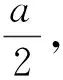
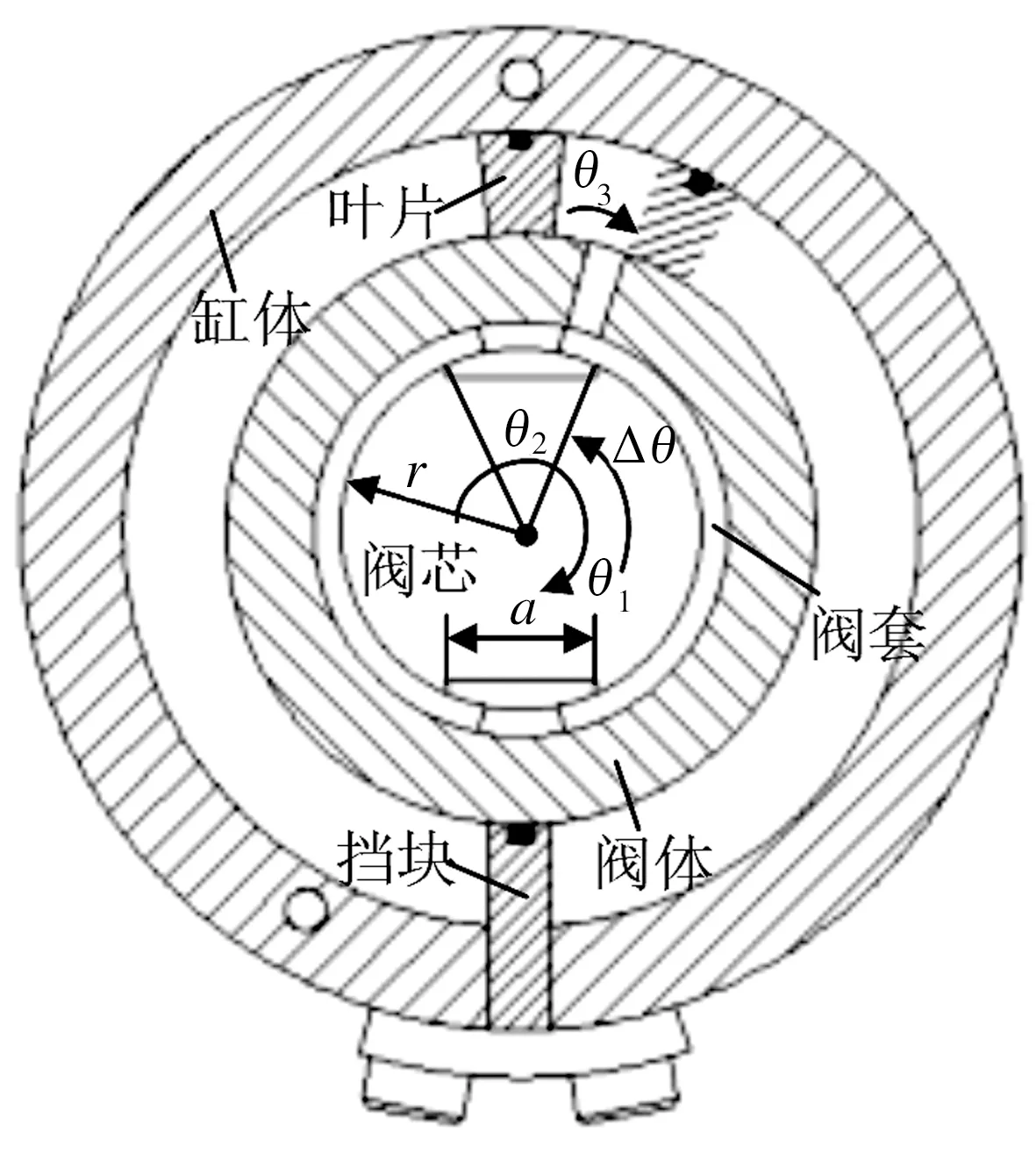
图6 阀口几何关系图

当阀芯相对于阀套顺时针转动时，开口面积变化有以下几种情况:

(10)

由液压系统流量平衡原理[14]可知，阀口负载流量qL的计算方程为：

(11)

式中，Cd为阀口流量系数，ps为系统供油压力，pL为负载压力，ρ为油液密度。

2.3 关节工作腔流量连续方程及负载力矩平衡方程

假定液压伺服被动柔顺关节连接管道中的压力损失和管道动态可以忽略，且液压关节所有工作腔内各处压力相等，在不考虑弹性负载影响的条件下，关节工作腔流量连续方程及阀体输出力矩与负载力矩的平衡方程分别为[15]：

(12)

(13)

式(12)～式(13)中，Dm为工作腔的角弧度排量，Ctp为工作腔总泄漏系数，Vt为工作腔及管道的总容积，βe为油液的体积弹性模量，J为关节和负载折算到配流轴上的总惯量，Bm为关节和负载的黏性阻尼力系数，TL为作用在输出轴上的任意外加负载力矩。

3 关节被动柔顺性分析

3.1 液压伺服被动柔顺关节的仿真模型与实验

基于式(7)～式(13)等关节动力学模型，借助MATLAB/Simulink工具箱，建立液压伺服被动柔顺关节系统的仿真模型如图7所示，该模型中各参数的初始值设置见表1。

图7 系统仿真模型图

表1 参数设置

往系统中分别输入单位阶跃信号和正弦信号(幅值为1)，采用变步长ODE45算法仿真，仿真时间为10 s，通过研究液压伺服被动柔顺关节在有、无碰撞干扰力矩条件下的位置跟随响应及柔顺度变化来分析与验证关节的柔顺性。此外，因仿真模型中的碰撞干扰力矩T不仅是液压被动柔顺关节高、低刚度模式切换的触发条件，同时也是碰撞发生以后关节柔顺性调节的重要依据，故而设计如图8(a)所示的半实物仿真试验台来采集碰撞干扰力矩。由于本研究中的液压关节采用被动柔顺控制，且整个碰撞过程持续时间较短，所以在无主动控制的情况下，可以通过上位机结合开发板及处理器调节电机来输出合适转速，同时使用电机配合柔性力臂来替代液压关节与加装了弹性装置的手持力传感器发生碰撞，当获取了碰撞干扰力矩T的数据散点之后，再利用MATLAB软件拟合出相应的碰撞干扰力矩曲线如图8(b)所示，将所得实验数据经理论力学计算处理后用于仿真模型碰撞实验，以此确保仿真结果更加准确。

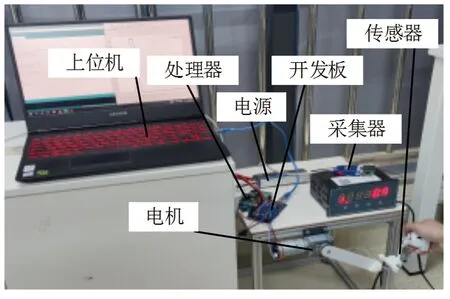
(a)碰撞干扰力矩采集实验台

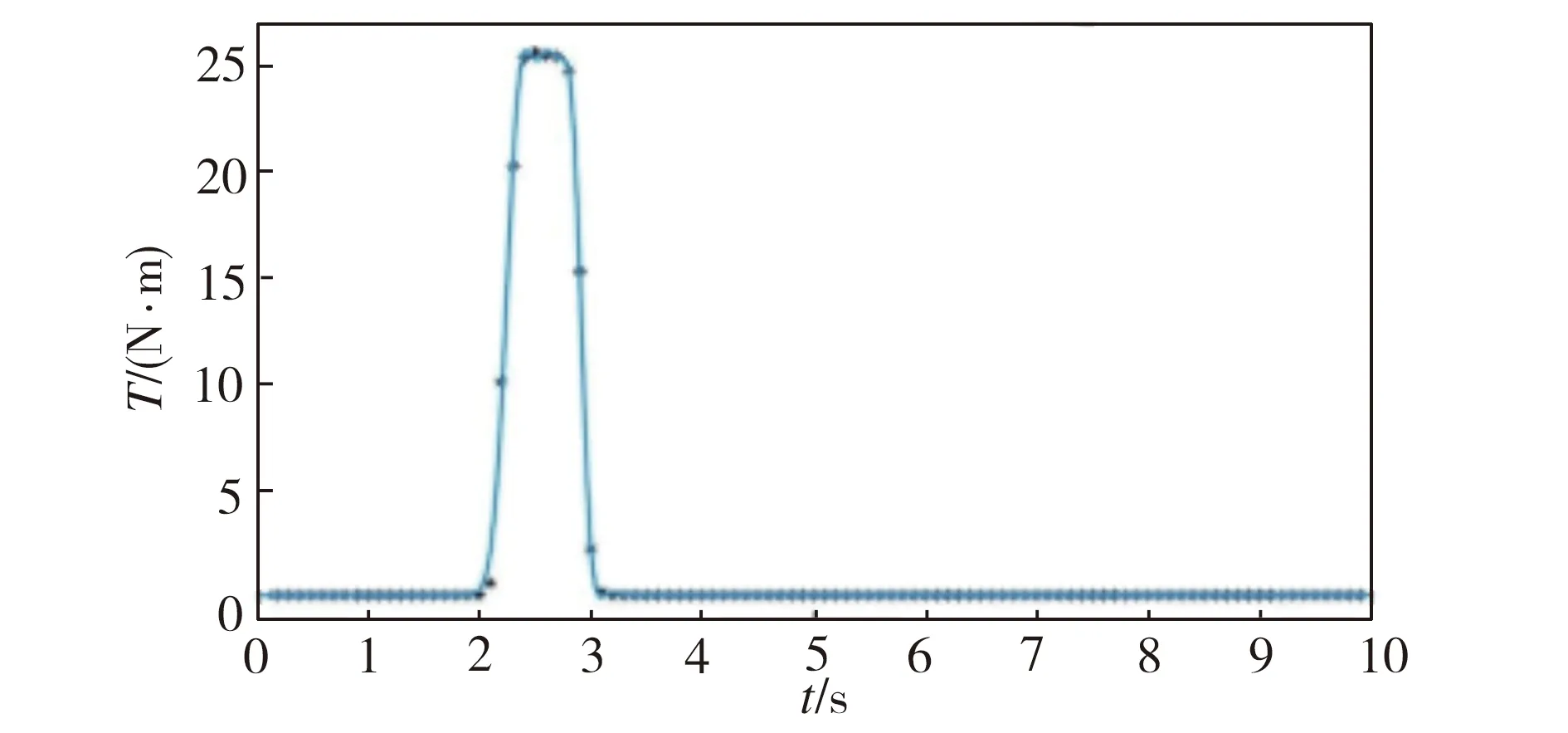
(b)碰撞干扰力矩曲线拟合

3.2 仿真实验结果与分析

往系统中输入一个幅值为1 rad的单位阶跃信号时，液压伺服被动柔顺关节的位置跟随响应仿真模拟结果如图9所示。从图9(a)～9(b)中可以看出，当关节未受碰撞干扰时，关节阀体输出转角经过0.72 s跟随转动1 rad并达到稳态,位置误差小于0.01 rad且超调量也较小；而由图9(c)～9(d)可见，当关节受到碰撞干扰时，阀体输出转角开始明显且迅速地回调，并在2.42 s时回调至谷底值0.473 rad，当碰撞结束后，液压系统随动性迅速恢复且未出现明显位置振荡现象。当系统输入信号为正弦信号时，液压伺服被动柔顺关节的位置跟随响应仿真模拟结果如图10所示。从图10(a)～10(b)中可以看出，在关节未受碰撞干扰时，其阀体输出转角变化曲线与正弦信号曲线基本重合，最大位置跟随误差不超过0.02 rad；而由图10(c)～10(d)可见，一旦关节发生碰撞，关节输出转角将产生位置回调以减小所受冲击，碰撞结束后关节随动性又立即恢复。仿真实验结果证明，本研究中的液压伺服被动柔顺关节不仅具有良好的位置随动性，同时也能对碰撞做出快速反应，表现出较好的柔顺性。

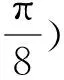
(a)无碰撞干扰力矩

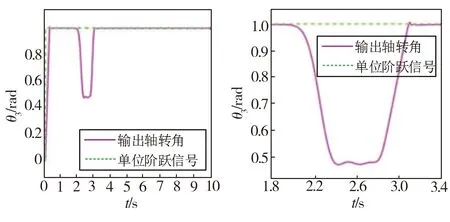
(c)有碰撞干扰力矩

(a)无碰撞干扰力矩

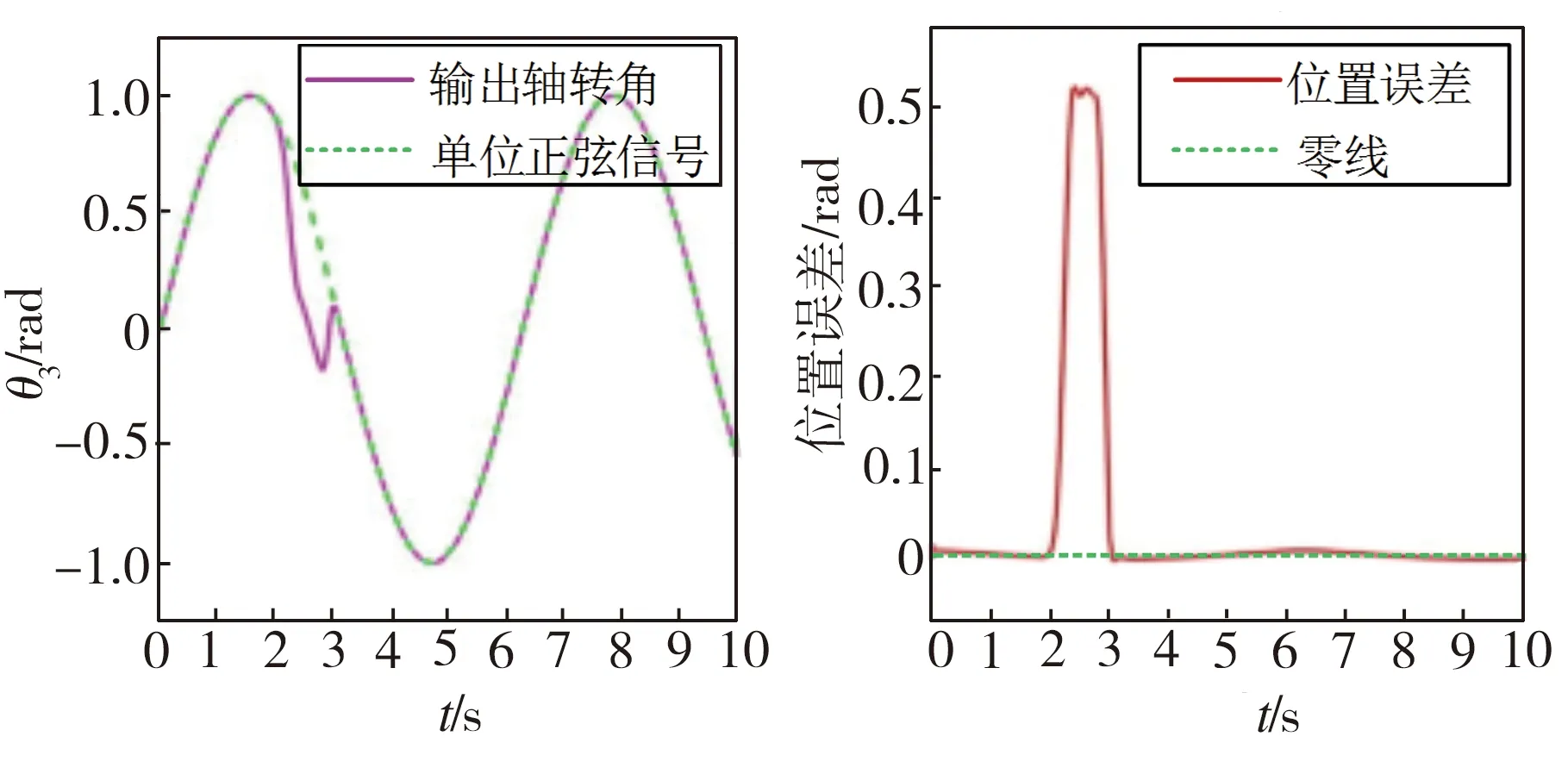
(c)有碰撞干扰力矩

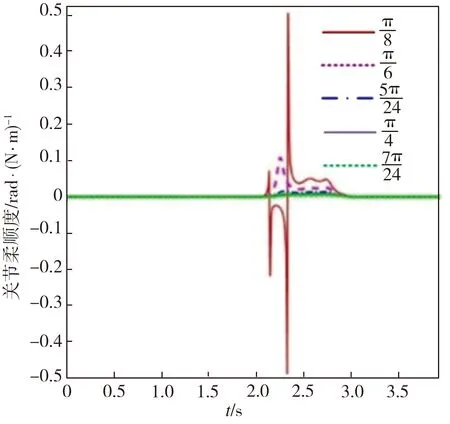
(a)不同斜坡角度γ,k=16000 N/m

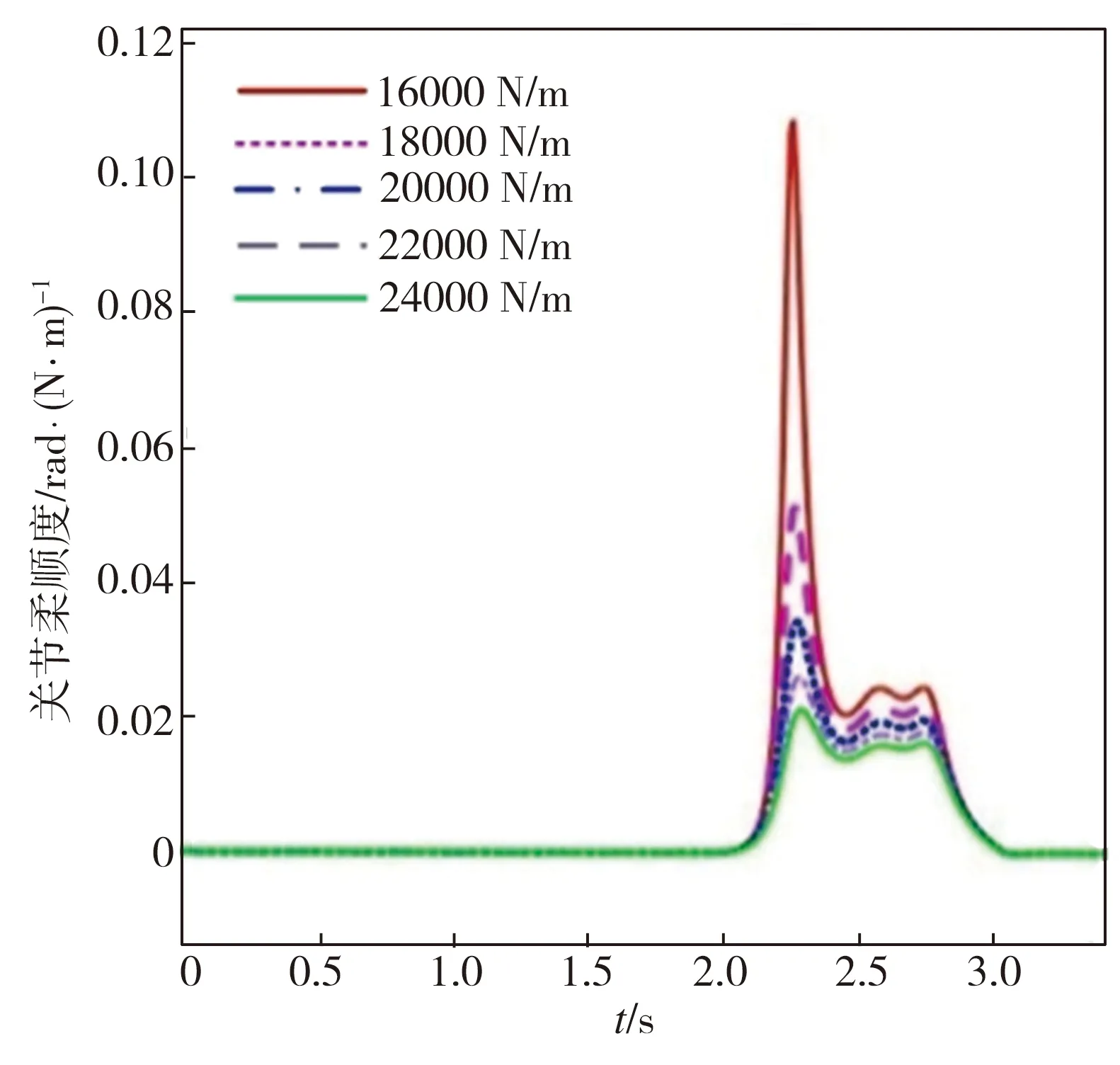
(b)不同刚度系数

4 结语

为了解决输出力矩较大的液压机械臂类机器人的人机物理接触安全性问题，本文在已有研究的基础上设计了一种液压伺服被动柔顺关节。首先对该关节的结构、工作原理和动力学模型进行了详细说明，然后通过MATLAB/Simulink工具箱建立关节仿真模型并进行了碰撞仿真实验，对关节的位置响应以及柔顺度进行分析，评估了意外碰撞瞬间液压伺服被动柔顺关节对碰撞进行处理的能力。仿真实验结果表明，该液压伺服被动柔顺关节具有良好的撞击随动特性，关节在发生碰撞时能够实现被动位置响应，向减小碰撞冲击的方向偏移，在碰撞结束后又迅速恢复位置随动性，且位置误差较小，基本能够按照设计的工作原理稳定运行，符合预期要求。此外，还引入了液压关节柔顺度的概念对该关节进行初步的参数优化。在后续工作当中，为了更好地验证和优化液压伺服被动柔顺关节的柔顺性，需要进一步对关节结构进行参数优化并制作关节样机，借助不同工况下的物理碰撞实验来提供更多的实验支撑。