超低频振荡主导机组的在线监控方法
马骞,杨荣照,朱泽翔,邓韦斯,李鹏,陈亦平,付超,姚文峰
(1. 中国南方电网电力调度控制中心,广州510663;2. 南方电网科学研究院,广州510663)
0 引言
近年来,实际电网出现的超低频振荡现象引起了工业界与学术界的广泛关注。在国际上,2011年哥伦比亚电网发生了由水轮机主导的超低频振荡现象[1];在国内,天广直流[2]、锦苏直流孤岛试验[3]、云南电网异步试运行期间[4 - 5]出现了振荡周期分别为10 s、14 s和20 s的超低频振荡现象,严重威胁电网的安全稳定运行。此外,相关研究表明,高水电占比的西南电网与华中电网异步运行后,存在超低频振荡的风险[6]。区别于传统的低频振荡,此类超低频振荡有如下特征:1)振荡频率低,一般低于0.1 Hz,远低于低频振荡0.2~2.5 Hz的范围;2)系统各节点频率同调变化,属于频率稳定范畴[7],与调速器强相关,区别于机电模式振荡。
研究表明,超低频振荡一般发生在高比例水电经直流送出系统[8 - 10]。文献[11]基于简化模型,揭示了超低频振荡是由水轮机一次调频控制过程小扰动不稳定导致的,退出负阻尼机组一次调频可平息振荡。文献[12 - 13]将全网机组的转子运动方程聚合,提出多机系统的超低频振荡分析模型。文献[14]研究表明超低频振荡阻尼与调速原动系统的阻尼转矩密切相关,水轮机调试原动系统在一次调频过程中提供负阻尼转矩。
在超低频振荡的抑制措施方面,文献[15 - 16]提出对水电调速器的PID参数优化提高超低频振荡模式阻尼。文献[17]提出一种基于Prony 分析的水电机组调速器PID 参数切换方法,用不同的控制参数实现分段控制,使得调速器能够同时兼顾一次调频性能和动稳阻尼水平。文献[18 - 19]通过在调速器侧增加附加阻尼控制环节,在提高超低频振荡阻尼的同时,兼顾一次调频的动态性能。
目前,超低频振荡的机理分析已相对成熟,但超低频振荡的在线监测及控制等相关研究仍较少,上述文献提出的离线参数优化由于受到模型与参数准确性的制约,难以完全规避系统超低频振荡的风险[20]。因此,亟待提出一种基于现有监控系统数据,准确可靠地对超低频振荡主导机组进行在线监控的方法。
本文分析机械转矩的阻尼特性,提出机械转矩阻尼的在线评估方法,为在线监测超低频振荡主导机组奠定了理论基础;进一步,基于现有监测系统的机组电磁功率与频率数据,提出一种超低频振荡主导机组在线识别与紧急控制的方法;最后,通过4机2区域系统仿真及实际PMU录波曲线对本文提出的方法进行校验。
1 超低频振荡阻尼特性分析
1.1 单机单负荷系统阻尼转矩分析
单机单负荷模型中水轮机原动调速系统一次调频过程的框图如图1所示。本节基于单机单负荷模型,研究超低频振荡过程中各状态的关系。

图1 一次调频控制过程框图
发电机的转子运动方程如式(1)所示:
(1)
式中:TJ为发电机惯性时间常数;Δω为角频率增量;ΔPm为机械功率增量;ΔPe为电磁功率增量;D为发电机阻尼。
忽略网损,发电机电磁功率增量ΔPe等于负荷有功增量ΔPL, 即ΔPe=ΔPL, 同时负荷只考虑频率调节效应,则ΔPL=KLΔω,KL为负荷频率调节效应系数。设调速原动系统的传递函数为Gm(s), 对式(1)进行拉氏变换,有:
TJsΔω=-Gm(s)Δω-(KL+D)Δω
(2)
式中s为超低频振荡主导特征根,s=σ+jωn, 则在其他特征根快速衰减后,有:
TJωnjΔω+(KL+D+TJσ)Δω=ΔPm(σ+jωn)
(3)
由此,可得到单机单负荷系统在振荡过程中,机械功率增量ΔPm、 电磁功率增量ΔPe以及角频率增量Δω在相平面上的关系图,如图2所示。
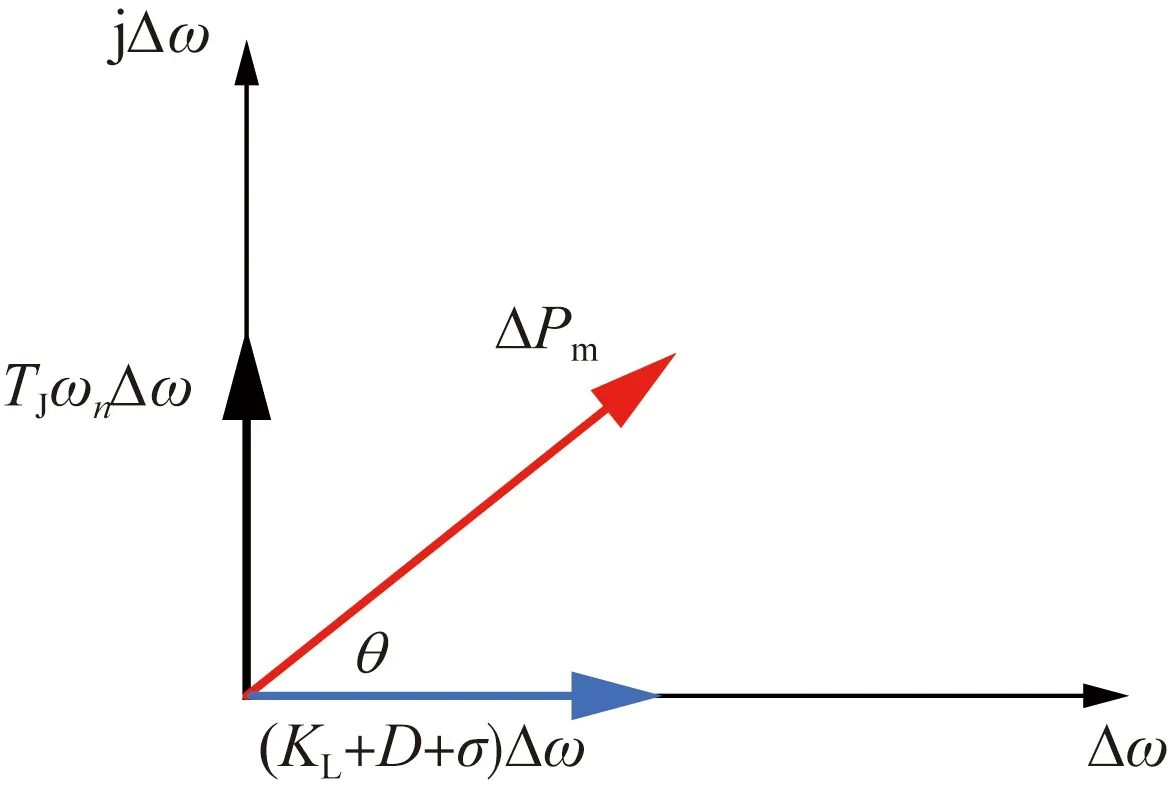
图2 振荡过程中的变量在相平面的关系图
对于单机单负荷闭环系统,在相位上,忽略网损和负荷的电压调节效应时,电磁功率增量ΔPe与角频率增量Δω同相,提供正阻尼。同理,发电机阻尼D亦提供正阻尼。
设调速原动系统传递函数为Gm=Kmd+jKms(Kmd为机械转矩的阻尼转矩;Kms为机械转矩的同步转矩),则机械功率在相平面上可分解为ΔPm(s)=-KmdΔω-jKmsΔω。 调速原动系统的阻尼性质与其相位滞后有关,由于原动系统输入量是-Δω, ΔPm超前/滞后-Δω的角度小于90°时(ΔPm位于第二、三象限),提供正阻尼,ΔPm超前/滞后角度大于90°时(ΔPm位于第一、四象限),提供负阻尼。
当Kmd+KL+D<0时,系统超低频振荡模式主导特征根实部σ>0, 系统整体阻尼为负。对于一般高比例水电大规模送出系统而言,认为发电机绕组阻尼D与负荷阻尼系数KL之和约为1,因此,当机组ΔPm在-Δω轴上的投影Kmd<-1时,认为该机组为超低频振荡主导机组,提供强负阻尼。
1.2 多机系统的阻尼转矩分析
在多机系统中各发电机状态方程可描述为:
(4)
式中i为第i台机组。
超低频振荡其中一个主要特征为系统各节点角频率近似相同[11],即:
Δω1=Δω2=…=Δωn=Δω
(5)
系统各发电机转子运动方程叠加,可得:
(6)
忽略网损,发电机电磁功率之和近似与总负荷功率相等,且全网角频率相同,仅考虑频率调节效应下,总负荷功率增量是角频率增量Δω的KLT倍,即:
(7)
因此,对式(6)进行拉氏变换,有:
(8)
式(8)与式(2)具有一致的形式,揭示了并列运行的各机组可以看做一个刚体,每台发电机机械转矩阻尼对系统超低频振荡模态阻尼的影响是线性叠加的,而各发电机阻尼转矩相互解耦[7]。因此,当系统发生超低频振荡时,可通过录波曲线识别主导机组,并退出其一次调频,从而抑制频率的振荡。
2 超低频振荡主导机组的在线监控方法
现有监测系统不能监测机组的机械功率,导致运行人员无法识别超低频振荡主导机组,无法快速平息超低频振荡。本节分析机械转矩的阻尼特性,提出机械转矩阻尼的在线评估方法,实现超低频振荡主导机组的在线辨识,并通过紧急退出主导机组一次调频,抑制系统超低频振荡。
2.1 机械转矩的阻尼特性分析
多机系统频率振荡过程中,若忽略机组阻尼D, 机组i的转子运动方程在频域上可描述为:
TJisΔω=-Gmi(s)Δω-ΔPei(s)
(9)
在单机单负荷模型中,由于只有发电机一个电压源,则不存在功角差,发电机电磁功率完全由负荷决定,电磁功率完全与角频率同向。而在多机系统振荡中,虽然机组电磁功率不再与角频率同向变化,但仍然满足单台机组的转子运动方程。因此,可通过转子运动方程转矩相量图分析机械功率增量ΔPm、 电磁功率增量ΔPe以及角频率增量Δω关系,从而利用监控系统的电磁功率与角频率的幅值与相角关系间接评估机组机械转矩的阻尼特性。
超低频振荡一般发生在高比例水电经直流送出系统中,由于直流频率限制器(FLC或FC)以及限幅环节的存在,振荡迅速到达等幅波动(即σ=0)。由此,在多机系统振荡过程中,令s=jωn, 不同阻尼机组的转矩相量的关系如图3所示。
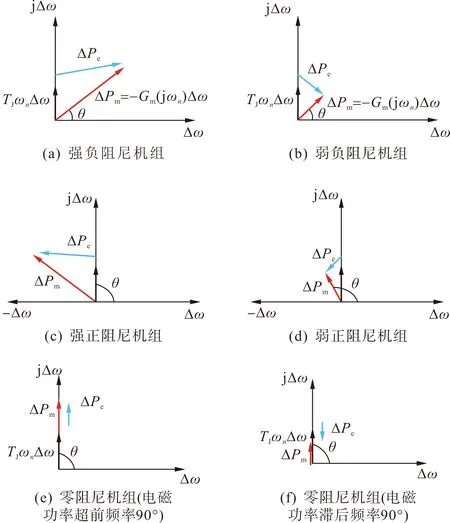
图3 转矩相量关系图
由图3振荡过程转矩相量图可知以下结果。
1)机械转矩提供负阻尼:此时,电磁功率增量ΔPe超前或滞后角频率增量Δω(0,90°), 机械功率增量ΔPm超前于电磁功率增量ΔPe, 如图3(a)、(b)所示。当机械转矩负阻尼足够大时,电磁功率增量ΔPe与角频率增量Δω近似同变化,如部分调速器采用联网参数的云南水电机组。
2)机械转矩提供正阻尼:此时,电磁功率增量ΔPe超前角频率增量Δω(90°,270°), 机械功率增量ΔPm滞后于电磁功率增量ΔPe, 如图3(c)、(d)所示。当机械转矩提供阻尼足够大时,电磁功率增量ΔPe与角频率增量Δω近似反向变化,如大部分一次调频调节性能良好的火电机组。
3)机械转矩提供零阻尼:此时,电磁功率增量ΔPe超前或滞后角频率增量Δω90°,如图3(e)、(f)所示。
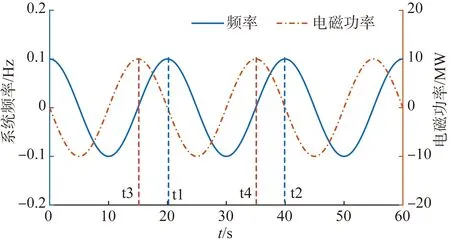
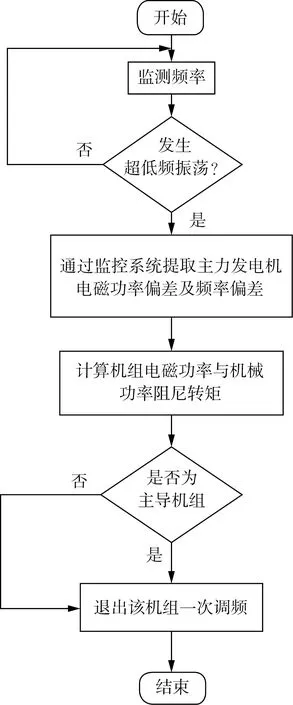
4)电磁功率增量ΔPe与角频率增量Δω的超前滞后关系:当机械功率增量ΔPm在该振荡模式的同步转矩较大时(即|Kms|>TJωn), 电磁功率增量ΔPe超前于角频率增量Δω;当机械功率增量ΔPm在该振荡模式的同步转矩较小时(即|Kms| 由图3相量关系图可得出在弱阻尼振荡中各变量间在相平面的数学表达式,有: ΔPmi(jωn)=jTJiωnΔω+ΔPei (10) 式中:ΔPmi为第i台机组机械功率增量;ΔPmi为第i台机组机械功率增量;ΔPei为第i台机组电磁功率增量;TJi为第i台机组惯性时间常数; 与机械功率相似,将发电机电磁功率在相平面上分解,即: ΔPe(jωn)=KedΔω+KesjΔω (11) 式中:Ked为电磁转矩的阻尼转矩;Kes为电磁转矩的同步转矩。 因此,式(10)可化简为: -KmdiΔω-KmsijΔω= TJiωnjΔω+KediΔω+KesijΔω (12) 由于实部虚部分别满足相等,对于单台机组的阻尼转矩和同步转矩,应满足: (13) 由式(13)可知,在零阻尼/弱阻尼振荡的情况下,机组机械阻尼转矩与电磁阻尼转矩大小相等、方向相反。 结合式(11)与(13),机组i的机械转矩的阻尼转矩为: (14) 式中:ΔP′ei为机组i的电磁功率增量标幺值;Δω′为系统角频率增量标幺值;Δθi为机组i电磁功率与角频率的相角差。 在Δθi的计算中,本文采用相邻过峰值计算方法,即通过检测ΔPei和Δω的各自两个连续的峰值点时刻,计算ΔPei与Δω的相角差,如图4所示。 图4 ΔPei与Δω的相角差关系示意图 由图4可得机组i电磁功率与角频率的相角差Δθi: (15) 式中:t1和t2分别为角频率增量Δω在一个周期内连续两个峰值的时刻;t3和t4分别为电磁功率增量ΔPei在一个周期内连续两个峰值的时刻。 因此,即便监控系统无法检测机组机械功率,也可通过电磁功率与角频率幅值、相位关系等信息,在线评估机组调速原动系统对超低频振荡的影响。 由上文分析可知,当系统发生零阻尼或弱阻尼的超低频振荡时,发电机机械阻尼转矩与电磁阻尼转矩大小相等,方向相反。因此,本文提出一种超低频振荡主导机组的在线监控方法,通过监测振荡过程中发电机电磁功率与角频率的振荡幅值及相位关系,间接计算机组机械功率提供的阻尼转矩,判定各发电机对超低频振荡的阻尼和参与情况,准确识别超低频振荡的主导机组,并退出其一次调频,抑制超低频振荡,如图5所示。 图5 超低频振荡主导机组的在线监控方法流程图 计算步骤如下所示。 S1:检测系统各主站节点频率,判断电网是否发生超低频振荡。若是,则触发策略。 S2:通过数据采集与监控系统提取主力发电机组的电磁功率ΔPei以及角频率增量Δω, 并进行归一化处理,得|ΔP′ei|与|Δω′|。 S3:基于式(15)计算主力发电机电磁功率增量ΔPei与角频率增量Δω的相角差Δθi。 S4:基于式(14)计算机组机械转矩的阻尼转矩Kmdi, 判断各主力机组机械阻尼转矩是否小于-1,即Kmdi<-1。 若是,则认为该机组为主导机组,并退出该机组的一次调频。 由于超低频振荡一般发生在高比例水电系统,本文基于BPA电力系统仿真软件建立4机2区域系统,系统共4台水轮机,每两台水电机组形成一个区域,两区域间通过交流联络线连接,如图6所示。发电机采用6阶模式,包含水轮机调速原动系统、励磁系统以及PSS。其中,G1-G4机组除调速器参数外均一致,额定容量为770 MW,机组开机容量700 MW,G4为平衡机。通过调整调速器参数,设置G1和G2为强负阻尼机组,设置G3和G4为正阻尼机组。系统超低频振荡模式阻尼比约为0。 图6 4机2区域系统 在第1 s施加15 MW的负荷扰动,机组G1、G2和G3的电磁功率及频率曲线如图7所示。如图7(a)所示,监控系统发出振荡警告,且各节点角频率同调变化(ΔωG1=ΔωG2=ΔωG3=ΔωG4), 判断系统发生超低频振荡,策略启动。 图7 4机2区域系统仿真曲线 通过数据采集与监控系统,有|Δf|=0.112 Hz,|ΔPeG1|=|ΔPeG2|=4.2 MW, |ΔPeG3|=2.2 MW, 归一化可得: (16) 式中:PbG1和PbG3分别为机组G1和G3的额定容量,Δf为频率增量;ω0为额定角频率;f0为额定频率。 如图7(b)、(c)所示,通过相邻过峰值方法,计算有ΔθG1=ΔθG2=3.213 4°,ΔθG3=223.966 0°。 因此,机械阻尼转矩有: (17) 由式(17)可知,G1与G2机组调试原动系统(机械功率)在振荡过程中提供强负阻尼,为主导机组;G3机组在振荡过程中提供正阻尼。退出G1与G2机组一次调频后,系统频率恢复稳定,如图7(a)所示。 云南电网异步试运行期间,在某直流功率调整小扰动试验中,云南电网出现振荡周期为20 s,频率在49.89~50.11 Hz之间的波动,持续约25 min,运行人员下令退出12台主力水电机组的一次调频后波动平息。图8给出了频率振荡过程中某水电厂和火电厂的电磁功率以及500 kV主变的频率。 图8 超低频振荡PMU录波曲线 如图8所示,监测到系统发生超低频振荡后,以40~80 s时间段计算。有系统频率增量幅值|Δf|=0.11 Hz, 水电电磁功率幅值|ΔPe水电|=5 MW, 火电电磁功率幅值|ΔPe火电|=17 MW, 归一化可得: (18) 式中Pb水电和Pb火电分别为某水电机组和某火电机组的额定容量。 如图8所示,通过相邻过峰值方法,计算有Δθ水电=-16.54°,Δθ火电=200.48°。 因此,机械阻尼转矩有: (19) 由式(19)可知,异步试运行期间,该水电机组调试原动系统(机械功率)在振荡过程中提供强负阻尼,该火电机组在振荡过程中提供正阻尼。运行人员退出12台主力水电机组一次调频后(12台机组共计发电功率约6 000 MW,约占当时云南机组总发电功率的27%),超低频振荡平息,印证了本文的分析结论。 本文基于阻尼转矩法,分析了多机系统振荡过程中机械阻尼转矩和电磁阻尼转矩的关系,提出一种超低频振荡主导机组的在线监控方法。主要结论如下。 1)基于阻尼转矩分析,从理论上推导证明了在弱阻尼/零阻尼振荡过程中,机组的机械转矩的阻尼转矩与电磁转矩的阻尼转矩数值相等,方向相反。 2)通过监控系统的电磁功率及频率数据,间接评估机组机械转矩的阻尼转矩,准确识别超低频振荡主导机组,并通过退出主导机组的一次调频,抑制系统超低频振荡。 3)通过4机2区域BPA仿真算例及实际系统超低频振荡录波曲线验证了本文所提方法的正确性与实用性,为运行人员提供理论与技术支持。2.2 机械转矩阻尼的在线评估
2.3 超低频振荡主导机组的在线评估与紧急控制
3 算例分析
3.1 算例1:4机2区域系统
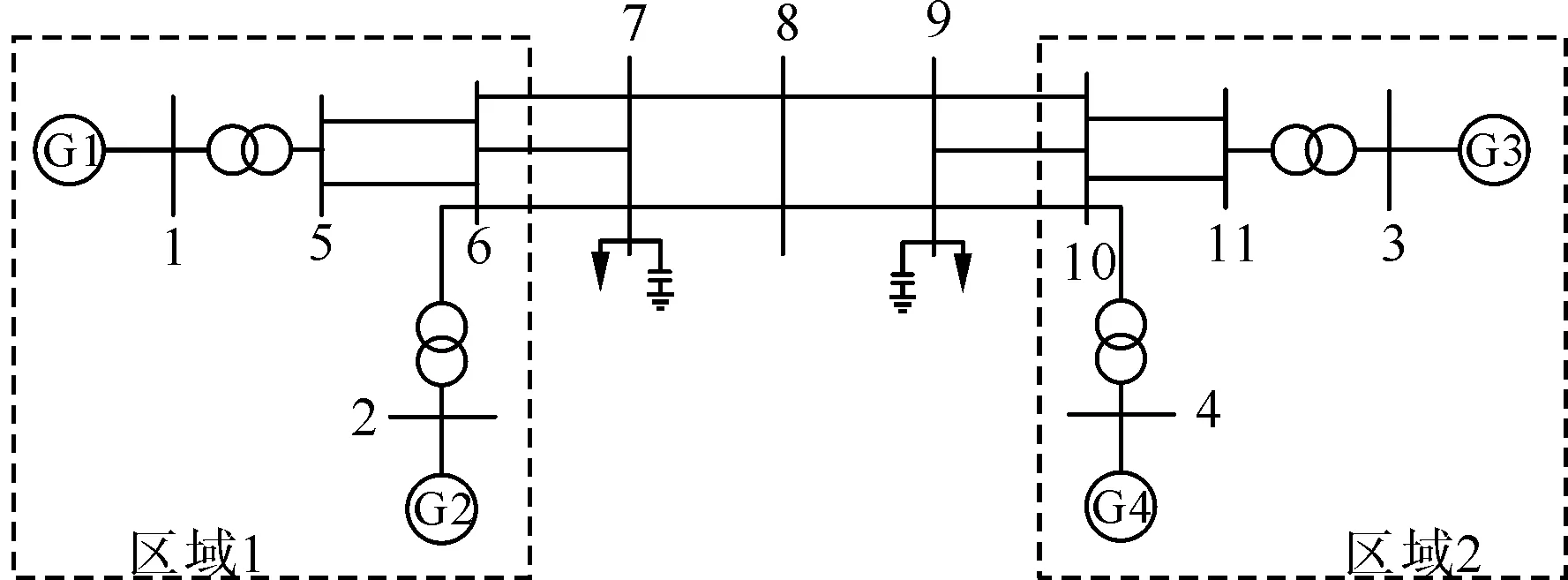

3.2 算例2: 实际系统超低频振荡PMU曲线分析

4 结论

