基于拓扑分群等值的不同拓扑下方向过流保护整定计算方法

陈朝晖，漆家炜，郑茂然，张弛，张静伟，吴江雄，李银红

(1. 中国南方电网电力调度控制中心，广州510663；2. 强电磁工程与新技术国家重点实验室(华中科技大学电气与电子工程学院)，武汉430074)

0 引言

采用反时限原则的方向过流保护(directional overcurrent relay，DOCR)具有原理简单、经济性好、易于协调配合等特点，在国外电网中已得到广泛应用[1 - 2]。国内电网也正尝试引入反时限过流保护[3 - 5]。考虑网络拓扑变化即不同拓扑下的DOCR整定计算是保障电网安全的一项重要基础工作。在实际的电力系统中，一旦遭遇如线路故障跳闸等紧急事件、设备运行维护和网络重新规划配置等运维需要后，电网拓扑则会受到不同程度的影响。当网络拓扑变化后，基于常规运行拓扑所得定值往往难以使得保护满足电网不同拓扑运行方式要求，容易带来主后备保护组失配的重大隐患[6 - 10]。此外，在我国当前保护装置定值普遍采用的“离线整定，在线不变”预整定模式的背景下[11]，保护离线整定计算必须考虑系统不同运行方式，以确保在线运行时不同拓扑下仍能正确动作。因此，开展计及不同拓扑的DOCR整定计算研究对于保障电网安全稳定运行具有重要意义。

在DOCR优化整定计算模型中，为了求得满足选择性的保护定值，需要将上下级线路的主后备保护组动作时间加以时间级差(coordination time interval，CTI)限制。当网络拓扑发生变化后，对于网络中的同一故障点而言，流经每个线路上DOCR的故障电流将会发生改变，从而导致保护的动作时间发生变化。因而考虑不同网络拓扑后，需要将在每种拓扑下的主后备保护动作CTI约束添加到传统反时限保护优化整定模型中。然而，这种做法不可避免地导致约束数量大幅增加。特别地，对于大型互联电力系统来说，本身主后备保护配合组数目就很多，再考虑不同拓扑下(即使考虑电网N-1事件)的级差约束，模型中不等式约束数量也会成倍数增加，很容易达到上万规模。由此导致优化整定计算模型难以甚至无法求解和定值性能欠佳的窘境，是面向不同网络拓扑下DOCR整定计算需要解决的一个关键难题[6 - 9, 12 - 13]。

针对考虑不同网络拓扑的反时限保护优化整定计算模型，文献[6]引入混合遗传算法来解决该非线性非凸优化模型中包含大量整定约束的难题，其具体做法是将该问题分解为两个子问题，并利用遗传算法求解非线性子问题以获得启动电流定值，然后利用线性规划算法确定时间定值。文献[7]通过将每对主后备保护组对应的一组不等式约束转化为区间约束，进而将该模型描述为区间线性规划模型，并基于数学理论化为标准线性规划问题，以此达到显著减少CTI约束数量的目的。上述文献所提方法的不足在于，求取定值的操作过程均较为复杂。文献[9]提出了部署双向配置反时限特性曲线DOCR和低带宽通信链路的解决方案，并引入了一种新的动态目标函数，最终实现保护的最佳配合。同样基于简单通信链路方案，文献[12]则利用数字保护装置提供的多定值区功能，提出用聚类技术实现每套定值对应一类拓扑的整定配合方案。然而，上述文献所提方案均依赖于通信技术，且对保护装置本身也提出了较高要求。

为了解决上述问题，本文试图从降低约束维度角度出发，提出了一种基于拓扑分群等值的不同拓扑下DOCR优化整定计算新方法。首先建立适用于整定计算的电网拓扑描述模型，并采用层次聚类法对拓扑进行分群，然后基于拓扑轨迹相似度指标计算每个拓扑集群的等值特征拓扑，最后建立仅含少量代表约束的基于等值特征拓扑的DOCR整定计算模型。利用IEEE 30节点算例验证了所提方法的有效性和优越性。

1 适用于整定计算的电网拓扑描述模型

电力网络拓扑指的是电力系统中主要的电气元件(发电机、变压器或电力线路等)互相连接所呈现的网架物理结构。然而，由于电网中发生紧急跳闸事件(如线路接地故障)、日常运行维护需要(如变压器停电检修)或者电力系统重新规划配置等导致该网络架构发生变化，则产生了不同电力网络拓扑。一旦拓扑发生变化后，网络中潮流分布也会改变，同理一旦发生故障，网络中的短路电流水平也会发生变化。对于安装在每条电力线路上的DOCR来说，不同拓扑下故障时测得的故障电流不再一样，因而根据动作曲线求得相应的动作时间也将发生变化。因此，在保护整定计算中，最直接反应每种网络拓扑不同属性的电气物理量便是每条线路上流过的故障电流。基于上述分析，故考虑利用故障电流建立适用于整定计算的不同电网拓扑描述模型。

设装设在所有支路两端的DOCR的总数为n， 不同网络拓扑的总数量为m， 则适用于整定计算的电网拓扑描述模型可表示为m种拓扑下流经n个保护的故障电流分布轨迹，如式(1)所示。

G=[G1,G2,…,Gi,…,Gm]T

(1)

式中拓扑i下的故障电流分布轨迹Gi定义为：

(2)

2 不同网络拓扑分群

2.1 电网拓扑分群指标

基于故障电流分布轨迹的拓扑描述模型很好地刻画了不同拓扑对于保护整定计算的影响程度。然而，每种拓扑下的不同网络结构影响了系统的节点阻抗矩阵，导致每种拓扑下各个支路上流过的故障电流水平完全不同，进而导致拓扑分群时使用的距离度量受此影响，因此直接应用上述拓扑描述模型很难准确对所有拓扑进行合理分群。为了更合理地实现对所有拓扑进行分群，必须构建在同一尺度下的拓扑分群指标。

变异系数是广泛用于概率论与数理统计学中的一种数据离散程度归一化量度的统计量，其定义为样本标准差与均值的比值。相比于单独的均值统计量反映数据平均水平或标准差反映数据离散程度，变异系数不仅综合了这2个统计量的特点，同时具有消除不同样本间测量尺度的优势。为此，可选取拓扑分群指标(topological grouping index，TGI)为：

(3)

2.2 电网拓扑分群算法

聚类是数据科学领域中常用于对不同的数据对象进行分组的一项无监督学习方法。对于给定的数据集，可以通过聚类算法将其划分成不同的群组。理论上，每个群组是一类特定数据对象的集合，数据间具有相同的属性或者特征，而不同群组数据间存在较大的属性或特征差异。利用聚类分析对数据进行分组后，可以更清晰地获取到一类数据信息。当前，聚类技术已在数据科学领域得到广泛应用，例如数据挖掘、模式识别、矢量量化、故障监测、语音识别等。迄今为止研究者们已经提出了许多聚类算法实现数据分群，常见的包括划分法(partitioning methods)、层次法(hierarchical methods)、基于网格的方法(grid-based methods)、基于密度的方法(density-based methods)、基于模型的方法(model-based methods)等[14]。

相比于其他聚类算法，层次聚类算法不需要预先指定集群的数目，允许使用者根据聚类层次结构结果选择最佳的集群数目以满足研究需要。再加上对数据间距离度量的选择不敏感，层次算法是众多聚类算法中较为流行的一种方法。具体地，层次聚类算法又可以分为“自底而上”和“自顶而下”两种实现方案。其中，凝聚层次聚类(aggregation hierarchical clustering，AHC)算法是采用自底向上形式对给定的数据集进行层次分解的方法。其基本思想是通过将每一个数据对象视为单个集群开始，不断地进行迭代凝聚，最终形成一个最大的集群。

本文选用AHC算法作为电网拓扑分群的算法。具体来说，对于给定的m种拓扑分群指标数据集，基于采用平均距离AHC算法的电网拓扑分群计算流程如下。

1)将每一个拓扑分群指标对象看作为一类，分别计算两两之间的平均距离；

2)选择距离最小的2个类合并为一个新类；

3)重新计算新类与余下所有类的平均距离；

4)重复步骤2)、3)，直至所有类合并成一类，形成层次结构。

其中，上述过程中求解2个类ci和cj之间平均连接距离dist(ci,cj)的计算公式为：

(4)

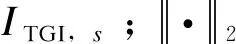
利用AHC算法进行拓扑聚类，最终形成所有拓扑种类构成的树状层次结构，根据需要指定集群数目后，得到每一集群中的拓扑种类。

3 等值特征拓扑计算方法

基于第2节的分析，拓扑集群是具有相似属性或特征的一种或多种拓扑的集合。这种相似属性或特征具体表现为每类拓扑集群下所有流经保护的线路出口故障电流的平均水平和离散程度较为相似。如此意味着反时限保护可以将这些相似拓扑视为某一种特定拓扑进行应对。每一集群下的这种特定拓扑，即为等值特征拓扑。

等值特征拓扑反映了所在拓扑集群的总体均值水平，因此最直接的计算方法是求取所有拓扑的均值。然而，由于适用于整定计算的电网拓扑模型是采用流经网络中所有保护的线路出口故障电流分布轨迹进行描述的，所以对所有拓扑下的故障电流进行均值计算所得结果仅仅是故障轻重程度的表征，其数据大小并不能代表系统中某一种真实存在的网络拓扑。因此，本文提出了基于轨迹相似度的等值特征拓扑计算方法。

基于轨迹相似度的等值特征拓扑计算方法，首先计算出拓扑集群的“虚拟等值拓扑”。假设对系统中所考虑的拓扑进行分群后共有k个拓扑集群C={c1,c2,…,ck}， 对于含有w种拓扑的任意一个集群ci={G1,G2,…,Gw}， 利用所有拓扑下故障电流均值水平表示该集群的虚拟等值拓扑模型，即：

(5)

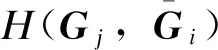
(7)

(8)

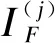
对于拓扑集群ci中w种拓扑分别计算与拓扑 间的双向Hausdorff距离，求得最小值的距离，即：

(9)

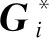
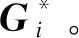
4 基于特征拓扑的DOCR整定计算模型

DOCR优化整定计算模型本质上以保护速动性作为目标函数，将选择性和灵敏性作为约束条件进行考虑。不失一般性，基于特征拓扑的DOCR整定计算模型建立如下。

1)优化目标函数

考虑速动性，取所计及的拓扑下所有保护动作时间之和最小为目标函数，即：

(10)

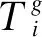
(11)

2)整定配合约束

为了保证同一条线路故障时不会发生越级跳闸事故，需要上下级线路保护构成的主后备保护配合组间满足级差约束。

(12)

(13)

(14)

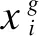
3)决策变量边界

考虑电力保护系统实际物理需求，对待求TDS定值和PCS定值加以上下限限制，用公式表示为：

TTDS,min≤TTDS,i≤TTDS,max

(15)

IPmin≤IPi≤IPmax

(16)

式中：TTDS,min、TTDS,max分别为TDS定值下限和上限；IPmin、IPmax分别为PCS定值下限和上限。

一般地，决策变量TTDS,i下限和上限分别取0.1和1.1；决策变量IPi下限考虑保护所在线路最大负荷电流，上限考虑其最小故障电流。

在不影响本文所提整定计算方法实施效果下，出于简单考虑，本文将上述DOCR整定计算模型考虑线性规划问题，即仅以TDS定值为决策变量，而PCS定值根据略大于负荷电流原则进行选取。相应地，上述模型可改写为：

(17)

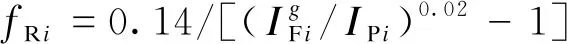
5 算例分析

5.1 测试系统概况

选用IEEE 30节点标准系统验证所提整定计算方法。系统接线图如图1所示，网络详细参数见文献[17]。该系统中包括6台发电机组、41条线路(含4条变压器支路)。基于环网线路两端配置反时限保护原则装设DOCR共82个，分别编号R1—R82。发电机采用简化次暂态模型，G1—G6次暂态电抗参数为：0.181、0.120、0.135、0.135、0.135、0.124。电力负荷采用恒定阻抗模型。

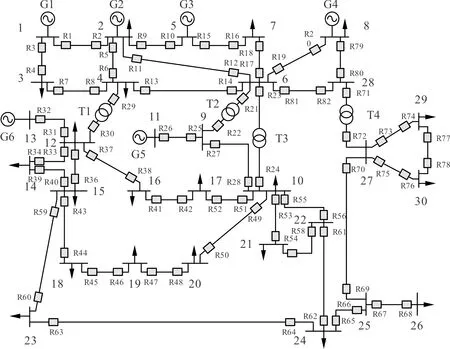
图1 IEEE 30节点系统单线图

沿用电网分析常用N—1原则生成不同网络拓扑，即考虑每条支路断开后的拓扑，加上主拓扑，则该网络共有42种不同网络拓扑，分别编号#1—#42。表1给出了每个DOCR按照1.2倍所有拓扑下支路最大负荷电流原则求取的PCS定值。

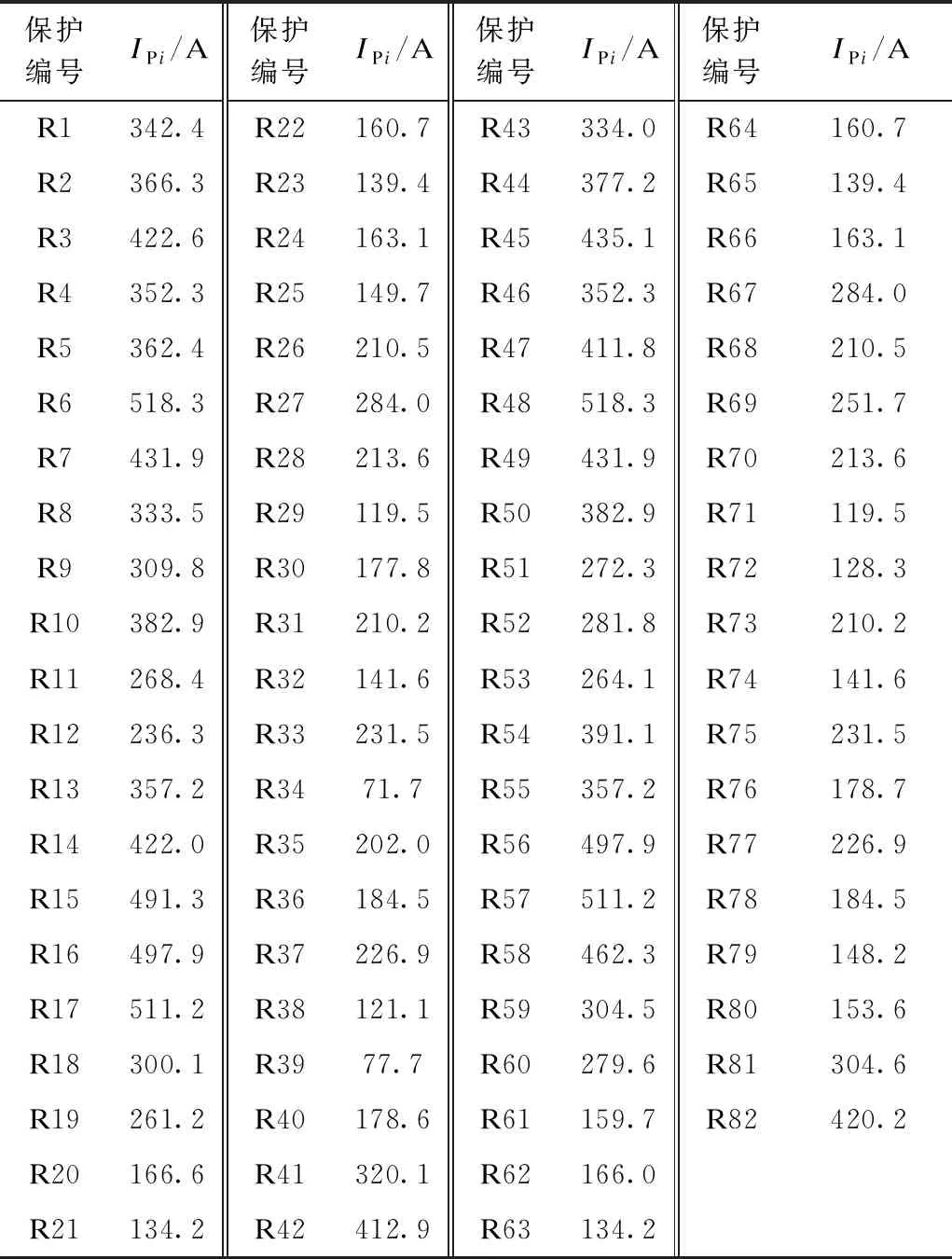
表1 保护启动电流定值

5.2 拓扑分群等值结果

对所考虑的42种不同网络拓扑利用所提方法进行层次聚类后的结果如图2所示。从图2中可知，使用层次聚类算法可以得到所有网络拓扑的层次关系。在所得拓扑层次关系树状图中，可根据需要设定拓扑集群数量k。 本算例中以6类拓扑集群和10类拓扑集群为例进行方案验证，即k=6和k=10。

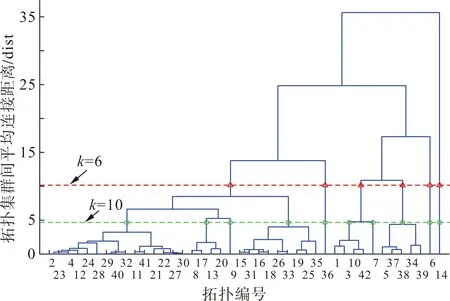
图2 拓扑分群所得层次关系树状图

结合图2可以发现，指定拓扑聚类的数目后，对应于每一类拓扑集群里面的详细拓扑编号顺应层次关系树状图向下搜寻即可得到。对于k=6和k=10两种情形下的每类拓扑集群下拓扑分群情况及等值特征拓扑结果，分别列于表2和表3中。

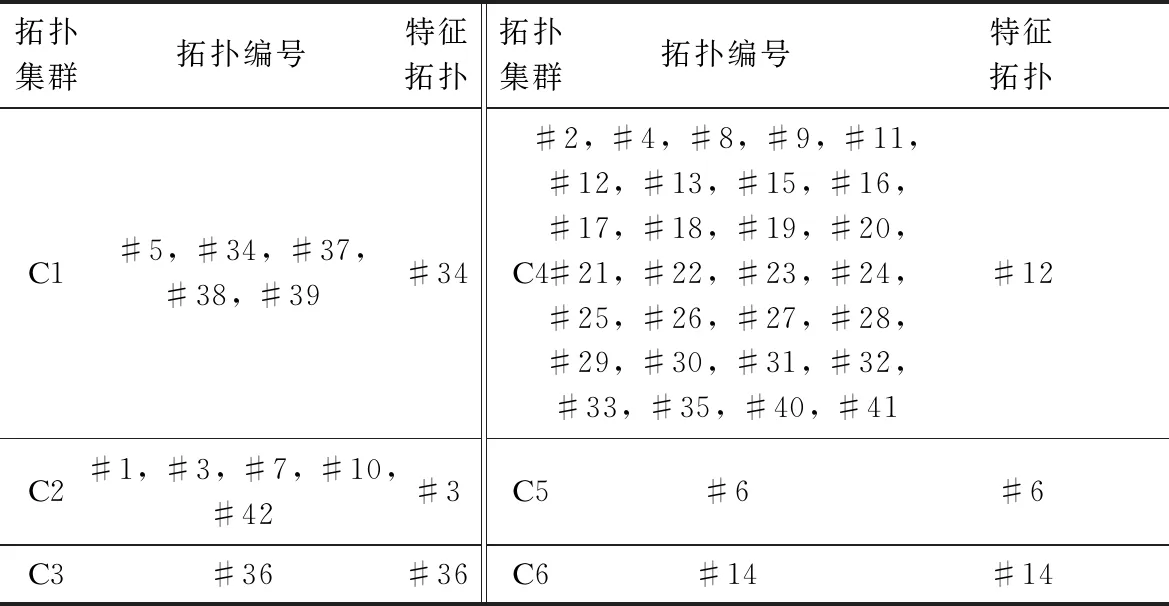
表2 拓扑分群等值结果(k=6)

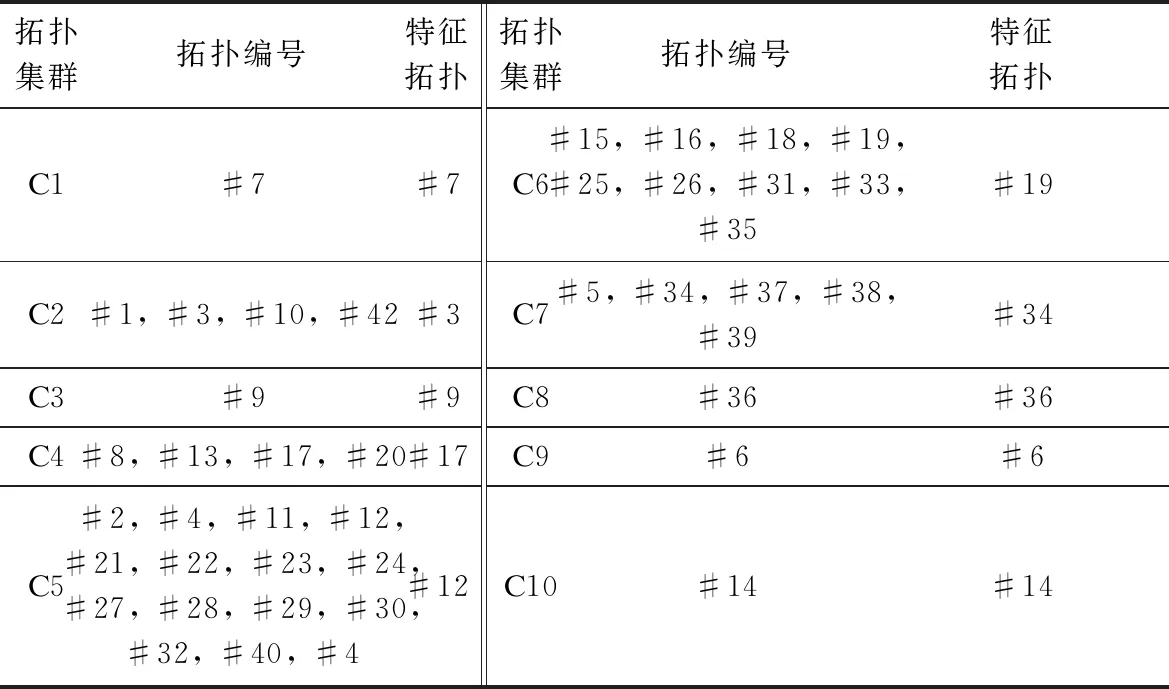
表3 拓扑分群等值结果(k=10)

在表2和表3中，每个拓扑集群下的拓扑种类数量是不完全一样的，具体每类拓扑集群下的拓扑种类是由该拓扑下故障电流轨迹分布决定的。以划分6个拓扑集群中C1为例。拓扑#34、#37、#38、#39分别对应于线路25- 26、27- 29、27- 30、29- 30退出运行后的网络结构。结合IEEE 30节点系统单线图可以看到，这4条线路相当于独立于环网主结构外的线路，结构上与环网结构耦合并非十分紧密，且所在节点无发电机电源，对其他线路故障点的短路电流贡献不大，所以在4条支路单独退出后的每个网络拓扑中，故障电流分布轨迹较为相似，即意味着所有保护测得的故障电流均值水平和离散程度大小较为接近。如此结果也表明，拓扑进行聚类分群后，所得每类拓扑集群下的拓扑具有相似属性或特征。

考虑篇幅限制，任取所得拓扑聚类分群结果中的一个拓扑集群(以设定k=6时拓扑集群C1和设定k=10时拓扑集群C6为例)，作出流经全网所有保护的故障电流分布轨迹，分别如图3所示。需要说明的是，由于某一支路退出运行后，该支路上的DOCR也将不再工作，故认为流经这条支路上2个保护的故障电流值为0，因而图3中对应该拓扑下的故障电流分布轨迹是不连续的。由图3可以看出，无论k=6时拓扑集群C1还是k=10时拓扑集群C6，其分别包含5种和9种拓扑下对应的故障电流分布轨迹均为形状高度一致的曲线，表明拓扑聚类结果的有效性。

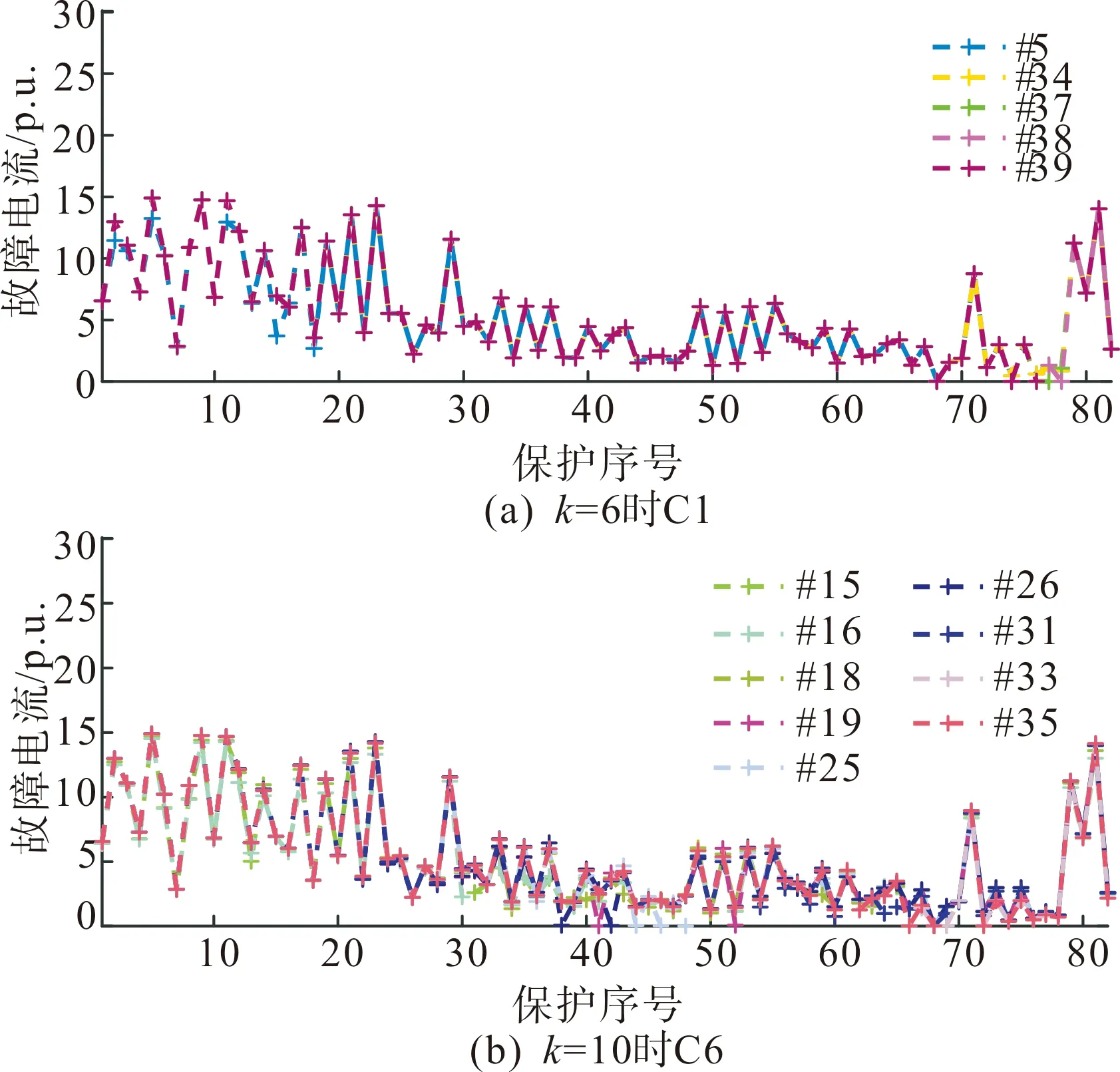
图3 拓扑集群中各拓扑对应的故障电流分布轨迹

进一步地，利用所提方法计算得到每一类拓扑集群的等值特征拓扑，分别列于表2和表3中对应拓扑集群的最后一列。可以看到，每类拓扑集群下均计算得到与之对应的唯一等值特征拓扑，因此保证特征拓扑数量与设定的拓扑集群数量保持一致。限于篇幅，同样仅以设定k=6时拓扑集群C1和设定k=10时拓扑集群C6为例，分别给出了拓扑集群中每个拓扑与对应的虚拟等值拓扑的相似度，相应结果分别如图4所示。

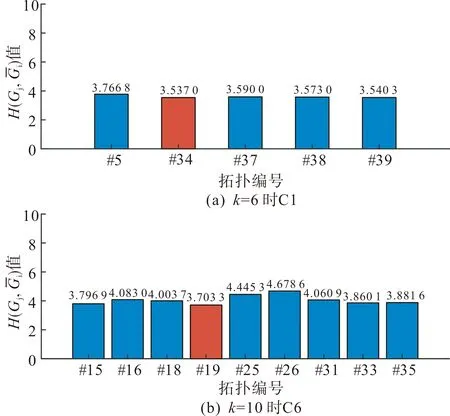
图4 拓扑集群中各拓扑与虚拟等值拓扑的轨迹相似度

在拓扑集群C1，由于拓扑#34与该类拓扑集群的虚拟等值拓扑间的双向Hausdorff距离值仅为3.537 0，相比于其他拓扑是最小的，因而选取拓扑#34作为拓扑集群C1的等值特征拓扑。同理得到拓扑集群C6的等值特征拓扑#19。同时可以发现，由于图3(a)拓扑集群C1中5种拓扑下故障电流分布轨迹几乎一致，因而图4(a)的每个拓扑与对应的虚拟等值拓扑的相似度值也十分接近；相比之下，拓扑集群C6中9种拓扑下对应的故障电流分布轨迹有个别地方存在不同，因而对应于图4(b)中的每个拓扑的相似度值存在一定差异。

5.3 所提方法下整定计算结果

以设定10个拓扑集群为例。利用所得10个等值特征拓扑建立DOCR优化整定计算LP模型，CTI值取0.3 s，TDS值上下限分别取0.1 s和1.1 s，调用MATLAB中LP求解器计算所得各保护TDS定值如表4所示。

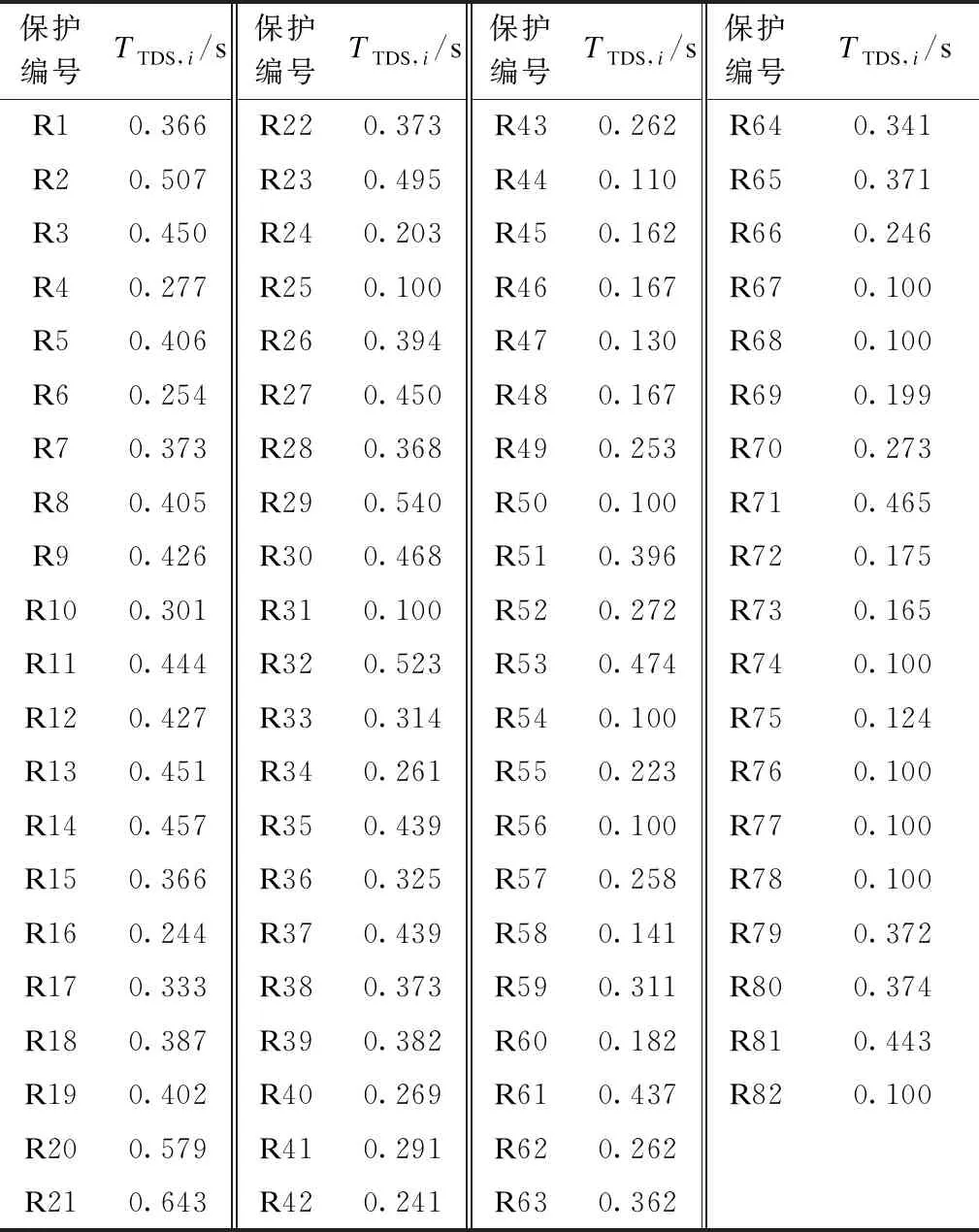
表4 所提整定方法下的待求时间定值

为了验证该方法下所得保护定值能够确保DOCR在不同拓扑下准确动作，需要判断每种拓扑下主后备保护组的选择性。限于篇幅，仅选取部分主后备保护组在部分拓扑下的动作时间进行比较。表5给出了保护组(R7, R3)和保护组(R42, R51)两对上下级线路主后备配合组在8种不同线路退出运行产生的拓扑中的主后备保护动作时间和时间差。可以看出，表5中所有保护组的Δt值均大于0.3 s，说明选择性能够有效保障。

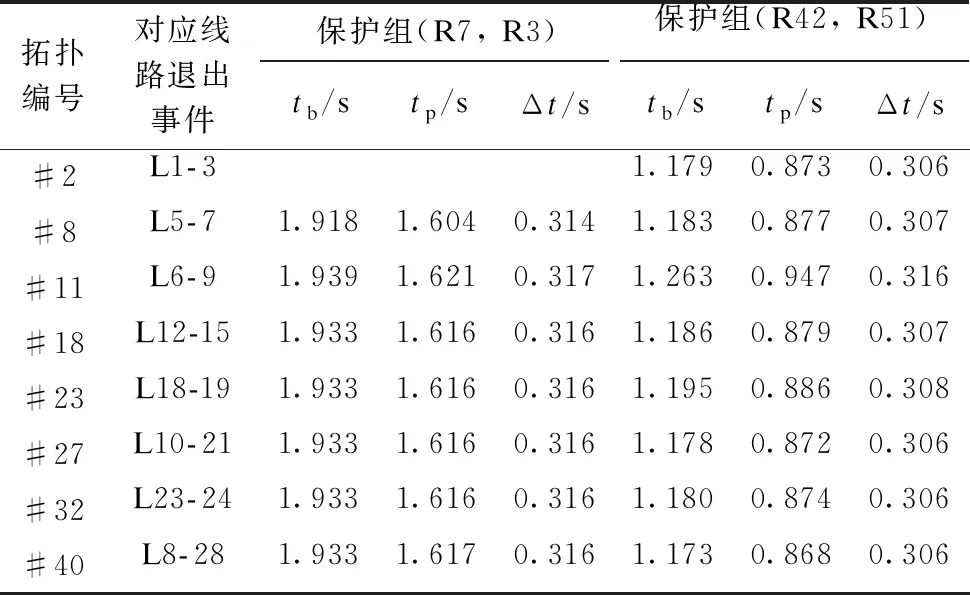
表5 不同拓扑下主后备保护组动作时间

5.4 与其他方法对比

为了验证所提整定方法的优越性，分别采用如下4种不同整定计算方法进行DOCR优化整定并将计算结果进行对比，结果如下。

1)方法1：仅考虑常规运行拓扑下的保护整定计算(即主拓扑#42)；

2)方法2：考虑所有不同拓扑下的保护整定计算(即拓扑#1—拓扑#42)；

3)方法3：本文所提方法下的保护整定计算(选取k=6和k=10两种场景)；

4)方法4：随机产生与方法3等数量拓扑下的保护整定计算(随机产生拓扑数量N分别取6和10)。

上述4种不同整定计算方法下的结果比较如表6所示。

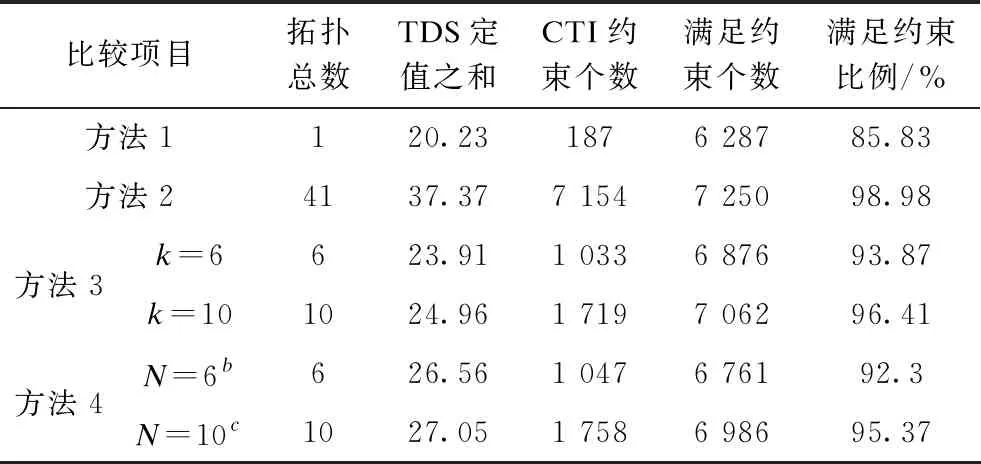
表6 4种不同整定计算方法的结果对比

1)满足约束比例/%：所有考虑的不同拓扑下CTI约束(不等式条件)总数量为7 325个；2)N=6b：b表示随机选取的6种不同拓扑分别为：#9, #28, #30, #32, #35, #42；3)N=10c：c随机选取的10种不同拓扑分别为：#2, #4, #11, #12, #13, #14, #15, #27, #28, #38。

由表6可知，方法1中由于仅考虑了常规运行拓扑，因而在所有方法下定值速动性能最优，即TDS之和最小，但是对于保护来说，凭借该方法下所得定值应对电网不同拓扑时，很多工况下主后备保护组失去了选择性，表现在所有拓扑下满足CTI级差约束比例最小，仅约86%。

为了提升保护面向不同拓扑的适应能力，方法2将所有不同网络拓扑全部考虑在优化整定模型中，然而求解该LP问题发现无最优解。由于本文研究重点并非寻找模型中的冲突约束，故尝试通过试错法移除拓扑#41后，即考虑余下41种拓扑后得到了该模型的最优定值，可以发现这种方法下保护选择性得到很好的保证，CTI约束满足比例接近99%，但不足的是TDS定值之和最大，达到了37以上，意味着较大地牺牲了保护速动性能。

方法3中基于拓扑分群等值，考虑拓扑数量仅为设定的拓扑集群数量，如此一来可以看到设定10个拓扑集群的场景下模型中只考虑1 000多个约束条件，仅为方法2中的1/4，所得保护TDS定值之和仅为24.96，相比方法1来说TDS定值之和只增加了5 s左右，但是CTI约束比例提高了约11个百分点，达到了96.41%。同时，k=6和k=10两种场景对比表明，适当增加拓扑集群数量，有利于提高保护定值的性能。因此，在确定实际电网的拓扑集群数量时，可以尝试选择不同的集群数量，比较求解的难度和定值性能，最终确定合适的集群数量。考虑到目前整定计算均为离线进行，增加部分计算时间在工程上是可接受的。

在方法4中，随机选取相同拓扑数量进行保护整定。需要说明的是，方法4中展示的结果是随机选取拓扑后得到的一组较好的结果。事实上方法4存在极大不确定性，所得结果优劣不均，且缺乏合理有效的理论支撑。由表6中最后2列给出的随机选取拓扑整定结果可知，同等条件下，与随机选取相同数量拓扑进行整定计算相比，所提方法下保护TDS定值之和更小，且所有拓扑下满足CTI约束比例更大，表明所提方法更能保证所求保护定值面向不同网络拓扑的优越性能。

综上分析，通过4种方法所得结果对比可以发现，与仅考虑常规运行拓扑下优化整定相比，所提整定计算方法可以较大提升保护面向不同网络拓扑的适应能力；与考虑所有不同拓扑整定方法相比，所提方法能有效避免约束过多导致优化模型无法找到最优解，并且在极大降低约束维度的同时，有效保证定值的优越性能。

6 结语

为了解决实际电网考虑不同拓扑后DOCR优化整定模型中庞大数量的不等式约束可能导致模型难以甚至无法求解的问题，本文从降低约束维度思路出发，提出了一种基于拓扑分群等值的反时限过流保护优化整定计算方法。在所提方法中，首先建立了适用于整定计算的拓扑描述模型，进而根据电网拓扑分群指标和聚类算法对网络拓扑进行聚类分群，然后基于拓扑轨迹相似度计算每个拓扑集群对应的等值特征拓扑，最后利用等值特征拓扑建立DOCR优化整定计算模型。在标准的IEEE 30节点系统中对所提整定计算方法的合理性与有效性进行了验证。算例分析结果表明，采用所提整定方法大大减少了优化整定模型中的约束数量，便于现有优化算法求取保护定值，同时所得定值能够满足保护面向不同网络拓扑运行的性能要求。下一步将开展自适应定值数目的保护优化整定计算方法研究，主要解决拓扑聚类时如何更加优化地选择拓扑集群数量的问题，从而在确保整定计算效率的同时优化定值的性能。