激光吸收涂层性能研究

张 磊，谢贤忱，吴 勇，王 平，武俊杰

（西北核技术研究所 激光与物质相互作用国家重点实验室 陕西西安 710024）

1 引 言

随着激光器向高功率、高能量方向发展，激光能量直接测量难度越来越大，国内外对激光能量直接测量方法开展了大量研究。目前，对激光能量的直接测量方式主要有吸收体式和水流式，通过测量吸收体或水的温升计算出入射激光能量。无论是吸收体式还是水流式测量方式，都需要在吸收体表面制作激光吸收涂层，用于提高入射激光的吸收效率，并将激光能量迅速转换为吸收体或水的热量。而涂层的厚度、吸收系数及热导率等参数决定了其对激光能量的吸收率[1-3]，同时也决定了能量在吸收体内的分布，从而影响了测量过程中热能损失的大小，进而影响到测量的准确度。研究激光能量吸收涂层特性对激光能量测量结果的影响对于激光能量测量装置的设计及能量反演计算具有重要的意义[4-6]。

本文建立了激光加载涂层样品模型，对激光能量光热耦合过程进行了简单模拟，得到了涂层反射率及涂层厚度对吸收体温升的影响。在Ф40 mm，3 mm厚的铜基底上制作了碳氮化硅(SiCN)材料，作为激光吸收涂层，对涂层表面反射率、漫反射特性及激光辐照下的损伤性能等开展了实验研究。

2 激光加载涂层样品模型与计算

考虑激光吸收涂层的具体应用场景及验证实验的可行性，建立了激光加载涂层样品模型，如图1所示。激光正入射到吸收体表面的涂层上，涂层吸收激光能量后使得自身及吸收体的温度迅速升高，激光加载过程中在吸收体背表面利用冷却水流对吸收体进行冷却。吸收体尺寸为Ф40 mm×3 mm，入射激光能量为Ein。换热过程中保持冷却水流温度及流速恒定。

图1 激光加载涂层样品模型Fig. 1 The model of coating sample irradiated by laser

入射激光能量被涂层吸收以后，通过热传导的方式将基底铜加热，使得基底温度迅速升高。根据传热学基本理论，涂层吸收的激光能量Q可以表示为[7]：

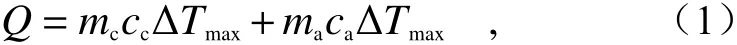
式中，mc、cc分别为涂层的质量和比热，ma、ca分别为吸收体的质量和比热，ΔTmax为温升。

入射激光能量为Ein，涂层样品对入射激光的吸收率为η，忽略传热过程中因对流、辐射等方式耗散给外界的热能以及涂层与基底温度梯度的影响，则可以得到温升ΔT与入射激光能量之间的关系为：

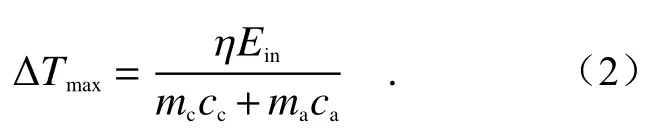
如图1所示，设涂层厚度为d1，涂层材料对激光的吸收系数为α，入射方向为z，入射面取z=0，则单位面积微元内所吸收的激光能量为

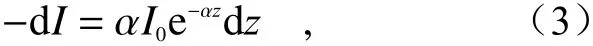
其中，I0为单位面积接收的光通量。计算时设置入射激光为均匀光斑，则入射过程中，考虑涂层内部产生的热能及对吸收体的反射吸收，则涂层内总的热源为[8-10]：

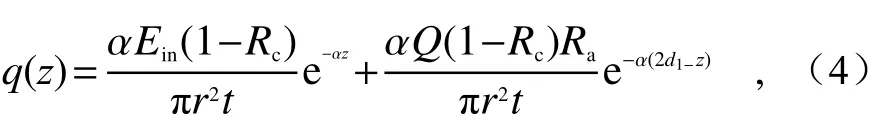
式中，r为光束半径，t为激光加载时间，Rc为入射面的反射系数，Ra为基底铜的反射率。

基底吸收激光能量后在表面产生的热通量为：

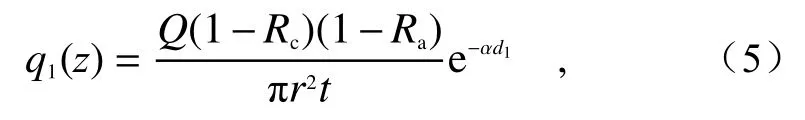
通过计算得到，涂层样品对激光的吸收率为：

涂层吸收激光能量后的三维热传导方程为：

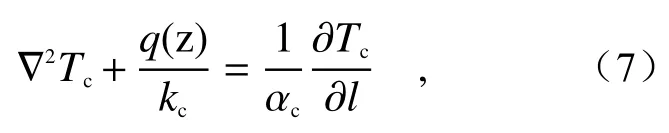
式中，Tc、kc、αc分别为涂层的温度、热导率和热扩散速率。吸收体铜的瞬态响应方程如下：

假设初始温度和环境参考温度为T0(T0=300 K)，面1和面2的初始条件为：

若εc、εa为涂层和吸收体的发射率，σ为Stefan-Boltzmann常数，面1和面2的边界条件为：

用hc和ha分别表示涂层和吸收体表面对流换热系数，其中hc为涂层与空气自然换热。ha为吸收体与冷却水之间的对立换热，假设传热过程中冷却水温度和流速均保持不变，计算过程中取

其中，L为制冷长度，Pr为普朗特准则数，ReL取决于制冷长度与水流速度。

理想情况下，假设涂层与吸收体之间接触良好，忽略接触热阻，可以得到分界面的边界条件如下：

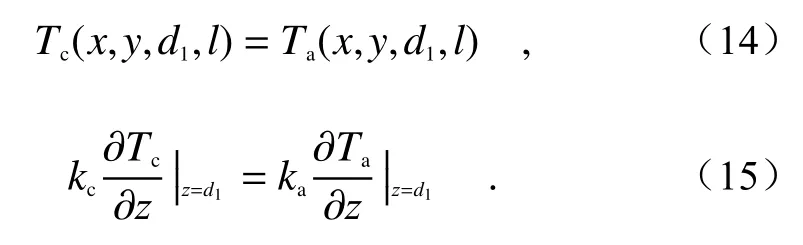
基于上面的模型，设入射激光功率为2 500 W，加载时长为30 s，外部温度为293 K，计算了不同制冷水流速度下吸收体的温升，如图2所示。

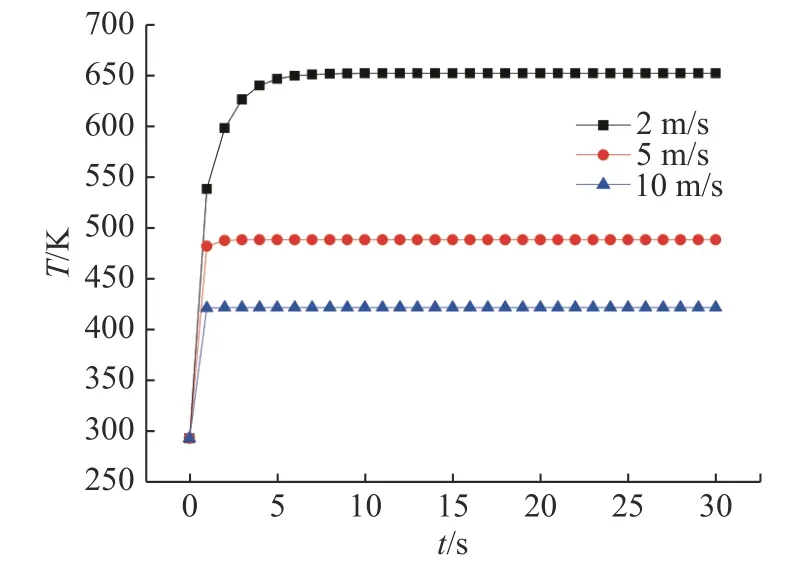
图2 不同制冷水流速度下吸收体温升Fig. 2 Temperature rise of the absorber at different waterflow velocities

固定制冷水流速度为5 m/s，改变入射功率，计算吸收体温升，如图3所示。

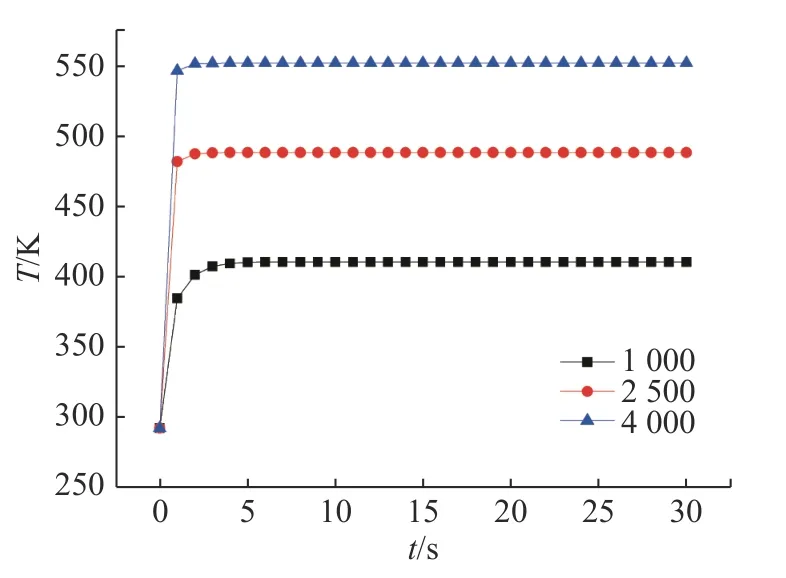
图3 制冷水流速度为 5 m/s时不同入射功率下的吸收体温升Fig. 3 Temperature rises of the absorber at different incident powers with the cooling water flow speed of 5 m/s

3 涂层表面反射特性

作为激光能量测量装置的吸收涂层，其表面反射特性决定了装置的光热转换效率及吸收体内的各向能量分布，直接影响装置对入射激光能量的测量准确性。为了提高吸收体对入射激光的一次吸收系数，吸收体涂层表面通常具有一定的粗糙度，而涂层表面的各向漫散射特性决定了能量在吸收体内的分布[11-14]。由此可知，涂层表面反射率及散射特性对激光能量测量装置的设计及能量反演计算具有重要意义。

由于涂层材料表面反射率通常具有波长选择性，针对不同波长激光能量测量装置的设计需求，在250～1 800 nm波长范围开展了不同材料涂层表面反射率测试实验。涂层表面反射率与激光波长的关系如图4所示。

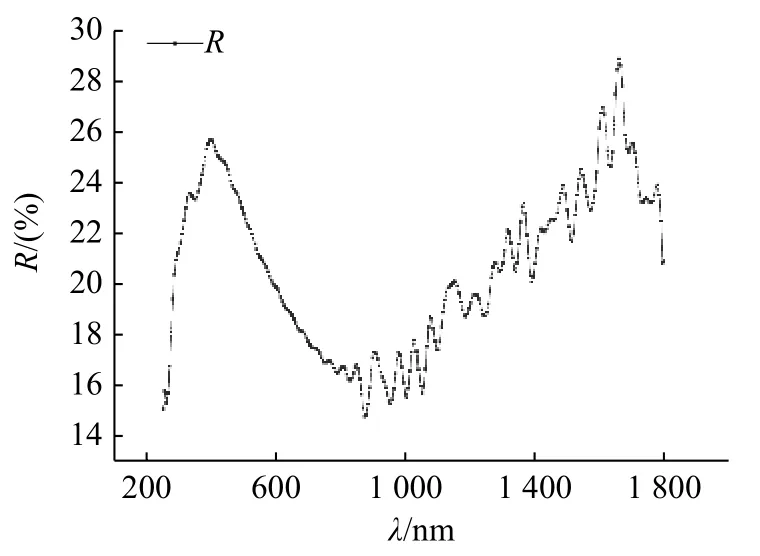
图4 涂层表面反射率与激光波长的关系Fig. 4 Relationship between reflectivity of coating surface and laser wavelength

涂层粗糙表面的散射特性会影响激光在吸收体腔内的多次反射和激光能量的后向逃逸率，因此，需依据涂层表面漫反射特性对能量测量装置进行结构设计，以控制装置的能量测量误差。

材料表面的双向反射分布函数(Bidirectional Reflectance Distribution Function，BRDF)能够反映光线照射在其表面后的散射特性。本文通过与标准漫反射板比对，对涂层表面进行了BRDF实验测试。图5（a）、图5（b）（彩图见期刊电子版）分别为正入射条件下涂层与BaSO4标准板BRDF的实验结果及不同入射角度下涂层BRDF实验结果。

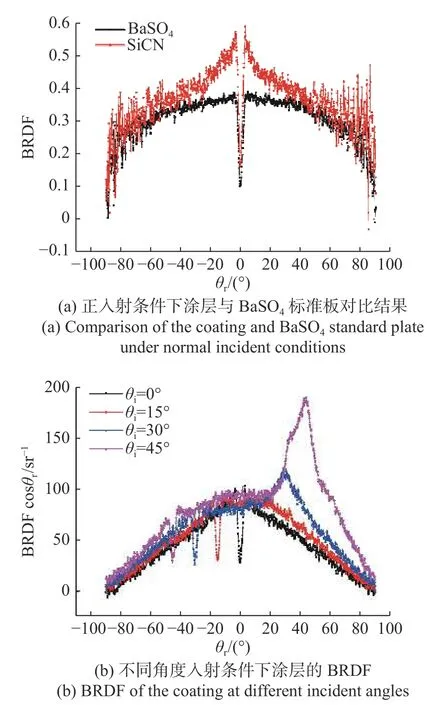
图5 涂层BRDF实验测试结果Fig. 5 Experiment results of the BRDF of the coating

由上述实验结果可知，与BaSO4标准板相比，所选涂层镜面方向反射光较强，光强约是最小光强的2倍。对于不同入射角度，当入射角小于15°时，可认为各向散射光是均匀分布的。

4 激光辐照涂层实验

为了满足高峰值功率的能量测量需求，要求吸收涂层具有较高的温度损伤阈值及抗激光损伤阈值。设计了涂层的激光辐照实验模型，调整辐照激光功率密度和辐照时间，对高峰值功率激光加载下的涂层损伤过程进行了实验研究，并与理论计算结果进行对比，得到了吸收涂层的抗激光损伤能力[11]。

实验采用1 064 nm激光源，利用高温相机实时测量涂层表面的温度变化，利用光电探测器实时测量涂层表面反射光强的相对变化。激光加载过程中，当反射到探测器的光强出现瞬间突变时，认为涂层表面出现了损伤。同时，利用摄像机实时记录涂层表面变化，监测其损伤过程。

当辐照激光功率密度由低变高时，得到涂层温升与入射功率密度的实验结果，如图6（彩图见期刊电子版）所示。

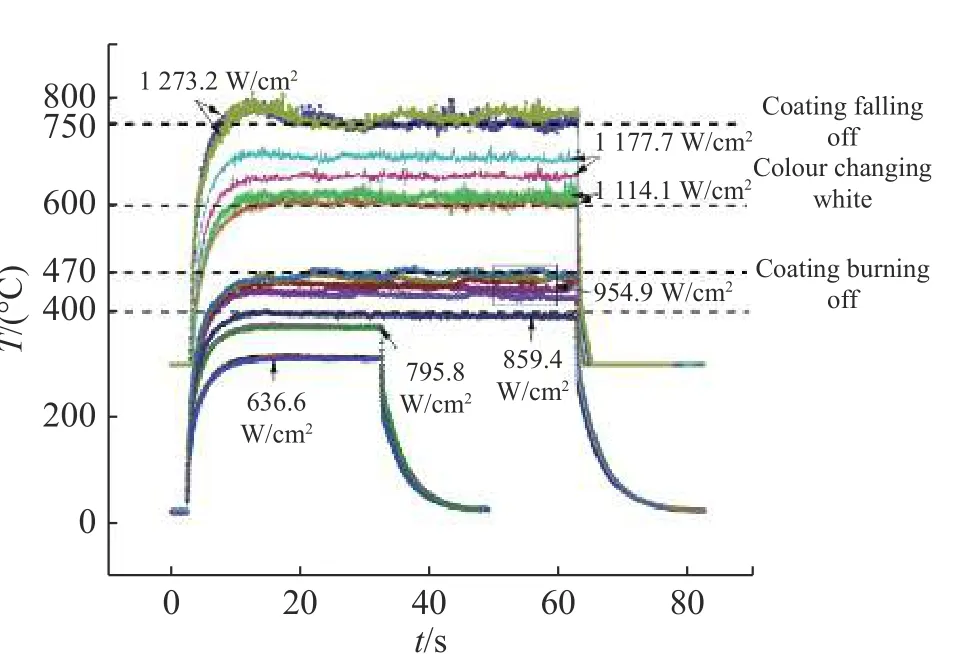
图6 涂层温升与辐照功率密度实验结果Fig. 6 Experimental results of the coating temperature rise with different irradiation power densities

由实验结果可以看出，涂层温度阈值在400 ℃左右，在该温度以下工作可确保无任何损伤，涂层可达到1 000 W/cm2、60 s的激光加载能力。图7（彩图见期刊电子版）为入射激光功率为2 500 W、辐照时长为60 s条件下实验值与计算值的比对结果。图中，曲线c为计算温升情况，曲线e为实验测量结果。可以看出，上述辐照条件下，涂层温升约为400 ℃，且模型计算结果与实验结果接近。

图7 相同激光辐照下涂层温升实验值与计算值对比结果Fig. 7 Comparison of experimental and calculated temperature rise values of the coating under the same irradiation conditions

5 结 论

本文针对能量测量装置的设计需求，选取了激光吸收涂层，建立了激光加载涂层样品模型并进行了能量耦合计算。基于铜基底碳氮化硅涂层开展了表面反射特性研究，实测了反射率及散射特性曲线。通过激光辐照实验获得了涂层温度阈值及抗激光损伤能力，实验结果显示：同样的激光辐照情况下，涂层温升的实验结果与模型计算结果吻合较好。