扭曲拉盖尔—高斯关联光束对大气湍流传输影响的抑制
张 滢,马超群,朱时军,刘晓旭,蔡 和,安国斐,王 浟
(1. 西南技术物理研究所,四川 成都 610041;2. 南京理工大学 理学院,江苏 南京 210094)
1 Introduction
In the process of free-space transmission, the laser beam will be affected by atmospheric turbulence, resulting in beam drift, light intensity scintillation and other phenomena that may degrade the beam transmission quality. Therefore, suppressing the influence of atmospheric turbulence through light field regulation has become an important research subject[1-5]. Researchers have found that the suppression effect of partially coherent light on atmospheric turbulence is stronger than that of completely coherent light. The theory of partially coherent light with twisted phase has been developed rapidly in recent 20 years. The concept of twisted phase was originally proposed by Simon and Mukunda et al. in 1993, and could not be decomposed into the product of two one-dimensional coordinate parameters at that time. Meanwhile, they theoretically constructed the theoretical module of twisted Gaussian Schell-model beam, and analyzed the transmission characteristics of this new beam[6]. In 1994, Friberg et al. combined previous theories with the first experiment in this regard to obtain the twisted Gaussian Schell-model beam, but their experimental optical path was complex with poor repeatability[7]. Because the magnitude of twisted-phase factor was limited by positive definiteness, not all beams could carry the twisted phase. Since then, the research has been limited to the common coherent beams. It was not until 2007 that the situation changed. In 2007,Gori et al. proposed the positive-definiteness criteria for the theory of reproducing kernel in Hilbert space, which provided an important theoretical support for the exploration of coherent structure in new stochastic light field[8]. Later, Borghi and Gori proposed the twisting conditions of axisymmetric Schell-mode correlated beam in 2015[9]. Then in 2018, they proved that the beam twisting was only related to the coherent structure of light field. They also provided the criteria for determining whether the coherent structure could carry a twisted phase[10-11]. By constructing a new coherent structure to regulate the phase, the anti-turbulence capability of the twisted beam can be further enhanced. In addition, the beam can carry orbital angular momentum[12-13], thus possessing an important application prospect in the fields such as free space optical communication, optical imaging and nonlinear optics[14-16]. As a novel beam with special correlation structure, Laguerre-Gaussian correlated (LGC)beam has received extensive attention from researchers in the application fields such as free space optical communication and optical capture. To study the suppression effect of a laser beam with special correlation structure and twisted phase on atmospheric turbulence, the Twisted Laguerre-Gaussian Correlated (TLGC) beam was specially chosen by this study to deduce the cross spectral density function and beam quality factor of this laser beam in atmospheric turbulence and to analyze its transmission characteristics.
2 Theoretical derivation
2.1 Derivation process
From the cross spectral density function at the source point of TLGC beam as well as the expanded Huygens-Fresnel diffraction integral formula and the atmospheric turbulence model, we derived the cross spectral density function and beam quality factorM2of the propagating beam. To visually display the theoretical derivation process, the flow chart of theoretical derivation is given below, as shown in Fig. 1.
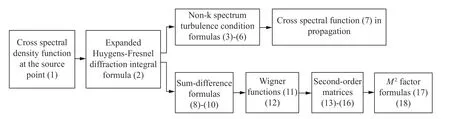
Fig. 1 Flow chart of theoretical derivation图1 理论推导的流程图
2.2 Cross spectral density function
If the beam propagates along the +zaxis and the TLGC beam is located in the source plane(z=0), the cross spectral density function of any set of position vectorsr1=(x1,y1) andr2=(x2,y2) can be expressed as:
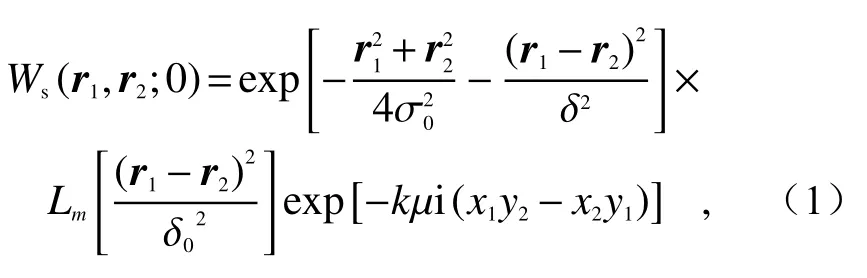
where σ0is the beam waist width, δ0is the crosssectional coherence,Lmis standard Laguerre polynomial of them-th order,kis the wave number, µ is the distortion factor, and
Un der the paraxial approximation condition,the cross spectral density functionW(ρ1,ρ2)=〈E∗(ρ1,z)E(ρ2,z)〉of a beam propagating for a distance ofzin atmospheric turbulence can be expressed as the following equation by using the expanded Huygens-Fresnel diffraction integral[17-20]:
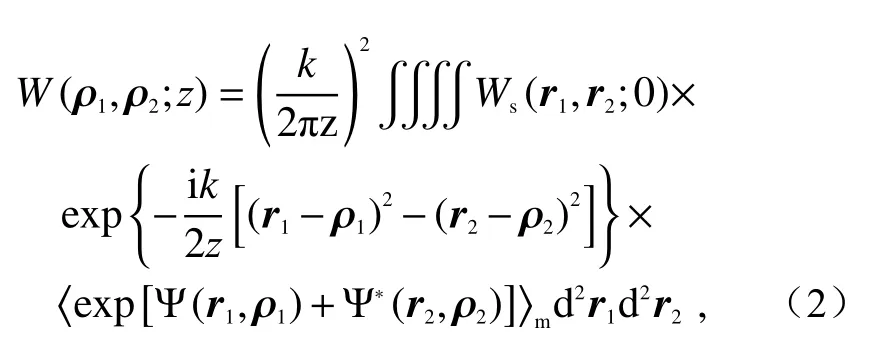
where “< >” represents the ensemble average; “*”represents the complex conjugate; ρ1=(u1,v1) and ρ2=(u2,v2)constitute any set of position vectors in the receiving plane; Ψ is the random term of complex phase when the spherical wave is transmitted from the source plane to the receiving plane in atmospheric turbulence. The exponential term containing the conjugate part can be written as[21]:

where Φn(κ,α) is the power spectrum function of refractive index fluctuation of turbulent medium, κ is the two-dimensional spatial frequency, and J0is the first class of zero-order Bessel function. If κ|u(r1−r2)+(1−u)(ρ1−ρ2)|≪1, J0can be approximately expressed as[22]:

According to Tosell's non-k spectrum turbulence theory, Φn(κ,α) can be expressed as[19]:

where α is the power index; κ0=2π/L0, κm=c(α)/l0;L0andl0respectively represent the outer and inner scales of turbulence;is the generalized refract ive index structure constant, in m3−α;1/(α−5),where Γ (·) is Gamma function.
The substitution of Eq. (4) and Eq. (5) into Eq. (3) can obtain:
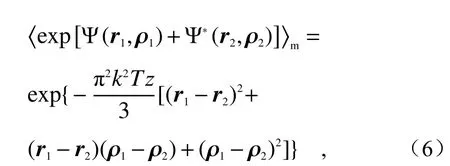
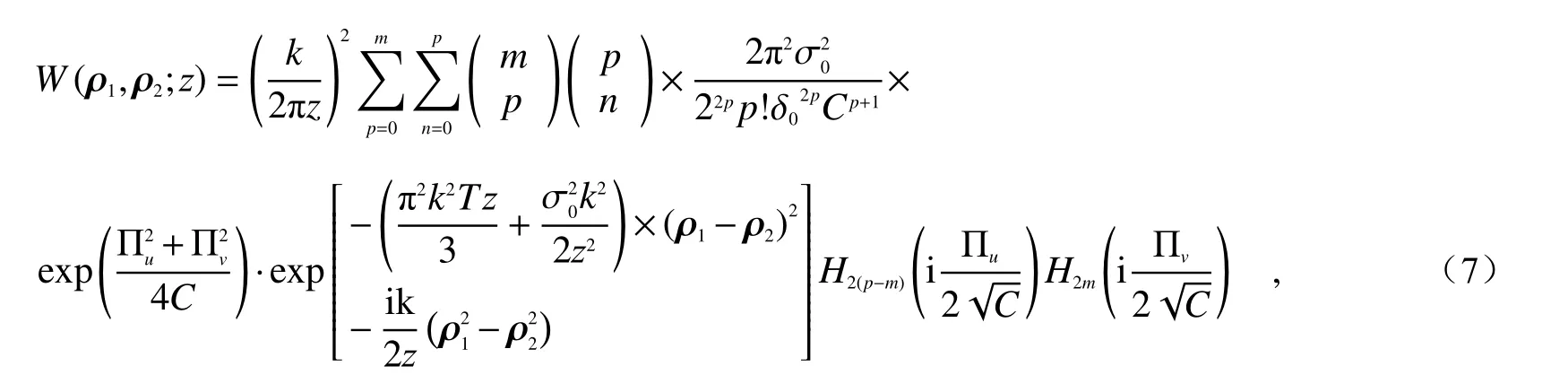
whereHm(·) is a Hermitian polynomial of them-th order;
2.3 Beam quality factor
The beam quality factorM2is an important index to evaluate the beam transmission quality in atmospheric turbulence. Based on the second-order matrix of Wigner distribution function, the factorM2of TLGC beam is calculated below. To simplify the calculation, the coordinate substitution is carried out, namely: ρs=(ρ1+ρ2)/2 and ρd=ρ1−ρ2. Then the Eq. (2) can be written in the sum-difference form:
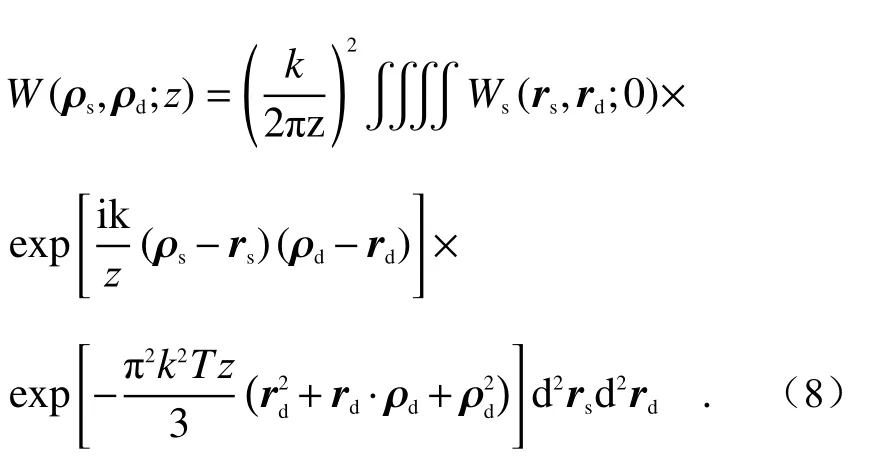
By using the algorithm proposed in the reference [23], we denoteandrd=. Then the Eq. (8)can be expressed as:
After substituting Eq. (6) into Eq. (2) and solving a series of integrals, the cross spectral density function of TLGC beam at the transmission distancezcan be obtained:
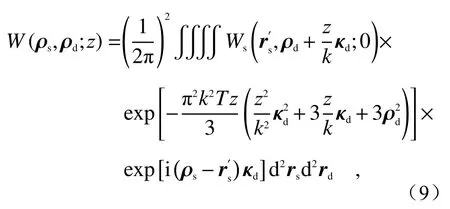
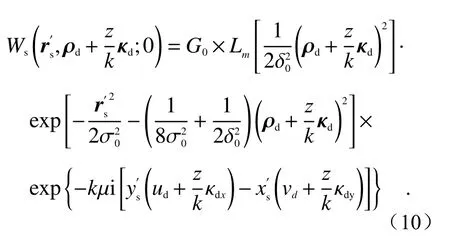
The Wigner distribution function of partially coherent light can be obtained through the two-dimensional Fourier transform of cross spectral density equation, i.e.:


Then1+n2+m1+m2-order matrix of the Wigner distribution function of partially coherent light is defined as[24-25]:
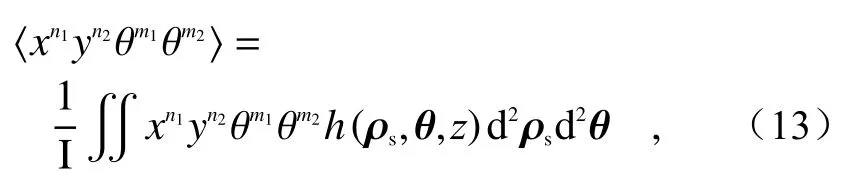
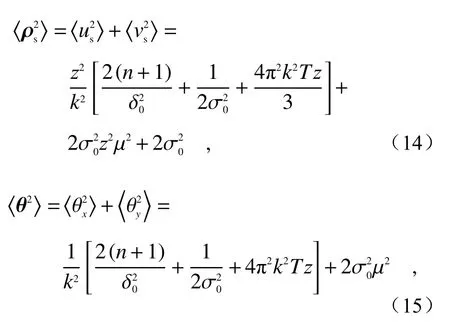

The factor M2of partially coherent beam after propagating in atmospheric turbulence is defined as the following second-order matrix[25]:
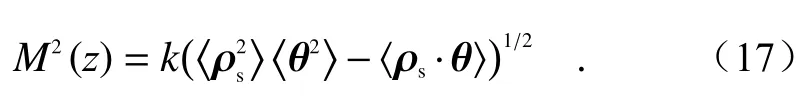
By substituting the equations (14), (15) and(16) into Eq. (17), the factorM2of TLGC beam after propagating in atmospheric turbulence can be obtained:
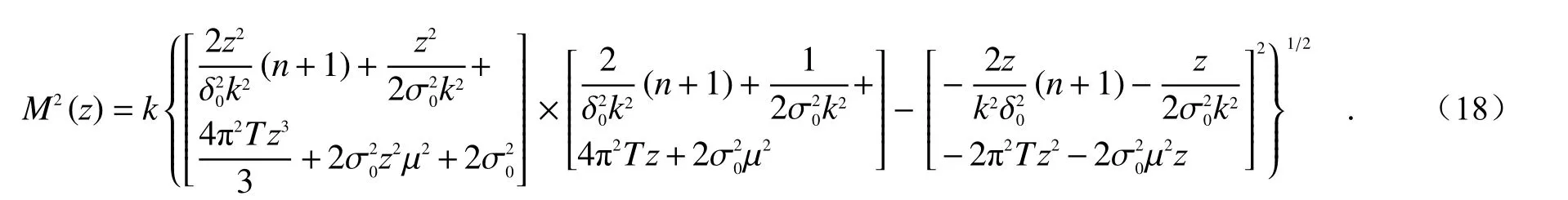
3 Numerical calculation and result
According to the theory of partially coherent light, the average light intensity of the beam arriving at the receiving surface is defined asI(ρ)=W(ρ1,ρ2). Based on the above definition, the average light intensity distribution of TLGC beam in atmospheric turbulence can be studied. When the parameters of laser beam and atmosphere are not given specifically, they can be selected as follows:
The average light intensity distribution curves of TLGC beam at different transmission distances are shown in Fig. 2. The average light intensity distribution of the beam near the source plane is Gaussian distribution. With the increase of distance, the beam is gradually hollowed due to the reciprocity between the initial coherent structure of light source and the far field intensity. When the propagation distance further increases, the average light intensity of the beam will be gradually degraded into Gaussian distribution under the influence of atmospheric turbulence. In addition, the ordermof TLGC beam will affect the rate of change of average light intensity distribution over distance. Ifm= 0,the TLGC beam will be degraded into the twisted Gaussian Schell-model beam. The higher the ordermis, the flatter the light distribution curve will be.This indicates that the higher-order beam has a stronger suppression effect on atmospheric turbulence.
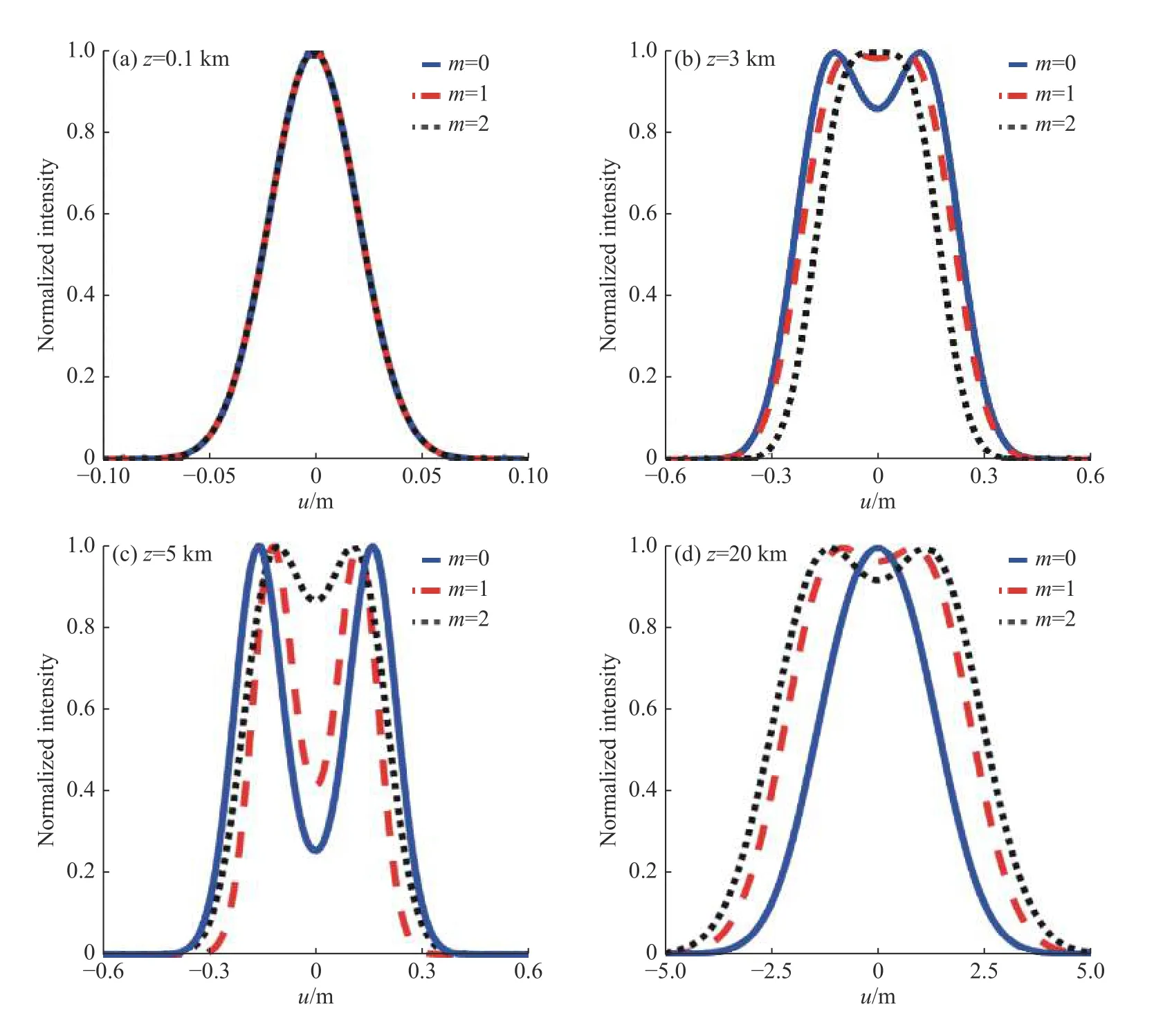
Fig. 2 Average light intensity distribution of a TLGC beam in atmospheric turbulence at different propagation distances图2 扭曲拉盖尔—高斯光束在大气湍流中不同传输距离下的平均光强分布
To analyze the influence of beam parameters and atmospheric parameters on turbulence suppression, we analyze the influence of the following parameters on average light intensity distribution atz=5km (see the Fig. 3): (a) power index α; (b) turbulent outer scaleL0and turbulent inner scalel0;(c) distortion factor µ; (d) cross-sectional coherence degree δ0. The influence of atmospheric parameters on beam propagation is shown in Fig. 3(a)−(b).When the power index α and the turbulent inner scalel0are smaller or the turbulent outer scaleL0is larger, the light intensity distribution will be converted into hollow distribution more quickly. In other?words, the stronger the turbulence is, the more obvious the variation trend of light intensity distribution will be. This is consistent with the conclusion in ref.[19], and also verifies the validity of the numerical calculation in this paper. The suppression effect of beam parameters on atmospheric turbulence is shown in Fig. 3(c)−(d). When the distortion factorµis increased or the cross-sectional coherence degree δ0is decreased, the transformation of light intensity distribution into hollow distribution will be slowed down, indicating that the influence of atmospheric turbulent environment on light intensity distribution will be suppressed.

Fig. 3 Average light intensity distribution of a TLGC beam in atmospheric turbulence at z =5km changing with different parameters: (a) power index α; (b) turbulent outer scale L0 and turbulent inner scale l0 ; (c) distortion factor µ and (d)cross-section coherence δ0图3 扭曲拉盖尔—高斯光束在z=5km 处不同参数影响下的平均光强分布。(a)不同功率指数α ;(b)湍流外尺度L 0和湍流内尺度l0 ;(c)扭曲因子µ ;(d)横截面相干度δ0
The Fig. 4 shows how the normalized factorM2of TLGC beam varies with the beam parameters and atmospheric parameters. The smaller the factorM2is, the higher the beam quality will be. From Fig. 4(a), Fig. 4(c) and Fig. 4(d), it can be found that for the beam with a higher orderm, itsM2factor changes more slowly and is less affected by turbulence. As shown in Fig. 4 (a), with the increase of the power index α, the normalized factorM2will increase rapidly at first and then decrease slowly,achieving the maximum value near α=3.11. This is because the atmospheric turbulence is strongest near α=3.11, producing the greatest effect on the beam.It can be seen from Fig. 4 (b) that the beam quality will decline with the increase of propagation distance in atmospheric turbulence. However, the increase ofM2factor can be slowed down by increasing the turbulent inner scalel0or decreasing the turbulent outer scaleL0, that is, by weakening the influence brought by atmospheric turbulence. In addition, compared with the decrease of the turbulent outer scaleL0, the increase of the turbulent inner scalel0has a more significant suppression effect on atmospheric turbulence. It is not difficult to find from Fig. 4(c) and Fig. 4(d) that with the increase of the distortion factor and the decrease of the coherence, the factorM2will be reduced and the beam transmission quality will be degraded, which is consistent with the conclusion of the previous analysis.
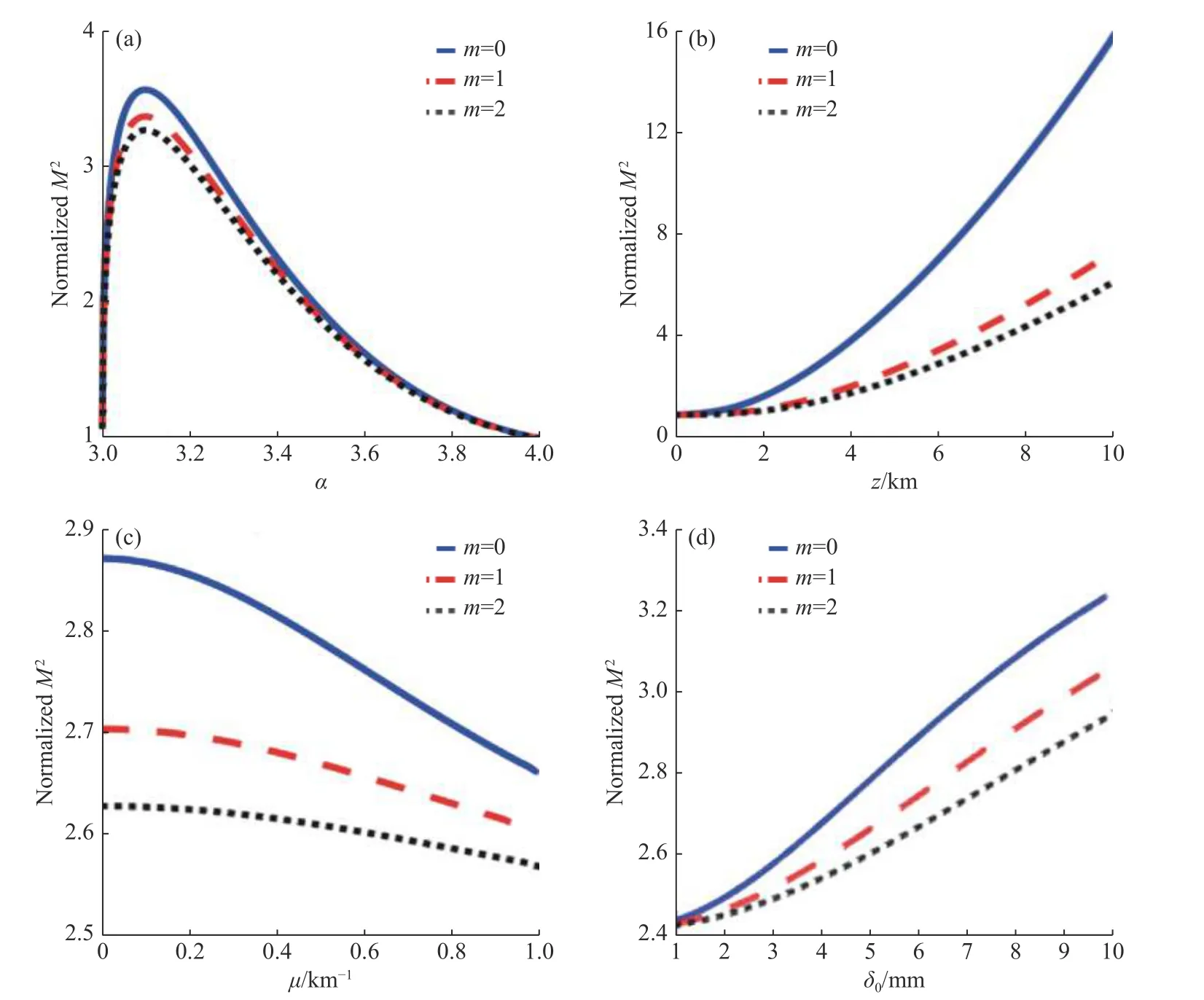
Fig. 4 Normalized M2-factor of a TLGC beam in atmospheric turbulence changing with different parameters: (a) power index α; (b) transmission distance z; (c) distortion factor µ; and (d) cross-section coherence δ0图4 扭曲拉盖尔—高斯关联光束在大气湍流传输中的归一化M2因子随不同参数的变化情况。(a)功率指数α ;(b)传输距离z;(c)扭曲因子µ ;(d)横截面相干度δ0
4 Conclusion
Based on the expanded Huygens-Fresnel principle and the Wigner function distribution, the negative effect of TLGC beam on atmospheric turbulence is investigated and suppressed. It is found by numerical simulation that the negative effect of turbulence on beam transmission quality can be effectively reduced by appropriately increasing the distortion factor of laser beam or decreasing the coherence of initial light field. For the TLGC beam, its transmission quality is affected by both beam parameters and atmospheric turbulence parameters. The TLGC beam with higher order, larger distortion factor and lower coherence has better transmission quality in atmospheric turbulence. However, the beam transmission quality will be degraded in the atmosphere with a larger turbulent outer scale and a smaller turbulent inner scale. The conclusion of this paper has certain theoretical guiding significance for the atmospheric communication and long-distance transmission of laser beam.
——中文对照版——
1 引 言
激光在自由空间的传输过程中受大气湍流的影响会出现光束漂移、光强闪烁等现象,这将导致其光束传输质量下降。通过光场调控来抑制大气湍流的影响已成为重要的研究课题[1-5]。研究者们发现,部分相干光对大气湍流的抑制效应比完全相干光要强,其中,携带扭曲相位的部分相干光理论在近20多年得到了快速发展。扭曲相位这一概念最初是由Simon和Mukunda等人于1993年提出的,它无法分解为两个一维坐标参量的乘积,他们同时理论构建了高斯-谢尔模光束被扭曲后的理论模块,并分析了该新型光束的传输特性[6]。1994年,Friberg等人结合前人的理论首次实验产生了扭曲高斯-谢尔模光束,但是,他们的实验光路复杂而且重复性较差[7]。由于扭曲相位因子的大小受正定性的限制,并非所有光束都能携带扭曲相位,所以,从那以后的研究一直局限于常见的相干光束。直到2007年,情况才有所改变,Gori等人提出了在Hilbert空间再生核理论的正定性判断条件,为探索新型随机光场的相干结构提供了重要的理论支撑[8]。之后,Borghi和Gori在2015年提出了轴对称的谢尔模关联光束被扭曲的条件[9],随后他们又在2018年证明了光束能否被扭曲只与光场的相干结构有关,并给出了判断相干结构是否能携带扭曲相位的判据[10-11]。通过构造新型的相干结构对相位进行调控,可以使扭曲光束抗湍流的能力得到进一步的增强,此外,还能使光束携带轨道角动量[12-13],这将在自由空间光通信、光学成像、非线性光学等领域有着重要的应用前景[14-16]。拉盖尔—高斯关联(LGC)光束作为具有特殊关联结构的新颖光束,在自由空间光通信和光学捕获等应用领域受到了学者们的广泛关注。本文为了研究携带扭曲相位的特殊关联结构激光光束对大气湍流的抑制效果,特地选择了扭曲拉盖尔—高斯关联(TLGC)光束,推导出了该激光光束在大气湍流中传输的交叉光谱密度函数和光束质量因子,并对其传输特性进行了相关分析。
2 理论推导
2.1 推导流程
文章从扭曲拉盖尔—高斯光束源点处的交叉谱密度函数出发,结合拓展的Huygens-Fresnel衍射积分公式和大气湍流模型,推导得到光束传输过程中的交叉谱密度函数和光束质量因子M2。为了直观显示理论推导过程,理论推导的流程图如图1所示。
2.2 交叉谱密度函数
假设光束沿z轴 的正方向传播,扭曲拉盖尔—高斯关联光束在源平面z=0内,任意一组位置矢量r1=(x1,y1)和r2=(x2,y2)所对应的交叉光谱密度函数可表示为:
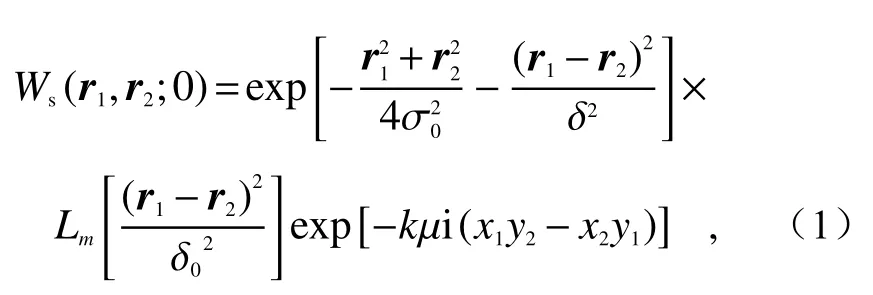
其中, σ0为光束束腰宽, δ0为横截面相干度,Lm是阶数为m的标准拉盖尔多项式,k为波数,µ为扭曲因子,
利用拓展的Huygens-Fresnel衍射积分计算,在傍轴近似条件下,当光束在大气湍流传输距离为z时,其交叉谱密度函数W(ρ1,ρ2)=〈E∗(ρ1,z)E(ρ2,z)〉可表示为[17-20]:
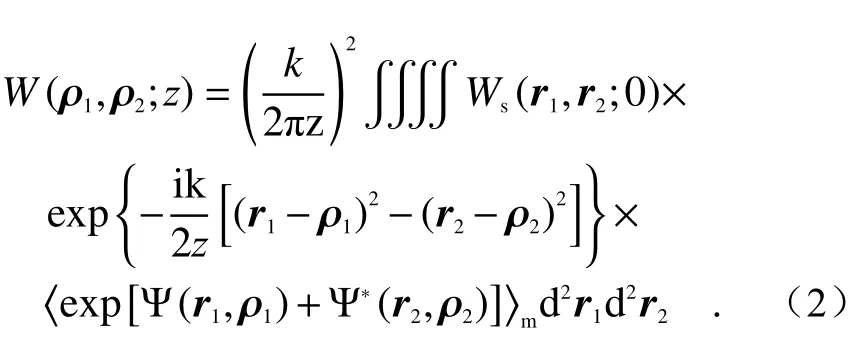
其中,“< >”表示系综平均,“*”表示复共轭,ρ1=(u1,v1) 和ρ2=(u2,v2)为接收平面内任意一组位置矢量。 Ψ为球面波在大气湍流中从源平面传输到接收面时复相位的随机项,含有共轭部分的指数项可写为[21]:
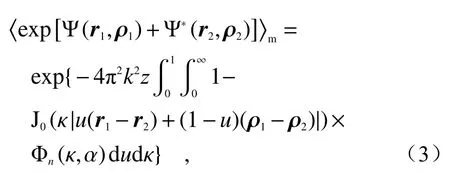
其中, Φn(κ,α)是湍流介质折射率起伏的功率谱函数,κ为二维空间频率,J0是第一类0阶贝塞尔函数,且当 κ|u(r1−r2)+(1−u)(ρ1−ρ2)|≪1时,可近似表示为[22]:
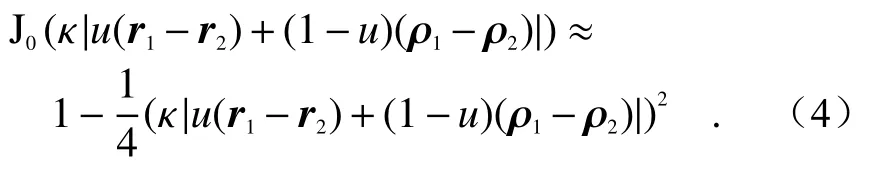
根据Tosell提出的非k谱湍流理论,Φn(κ,α)可表示为[19]:
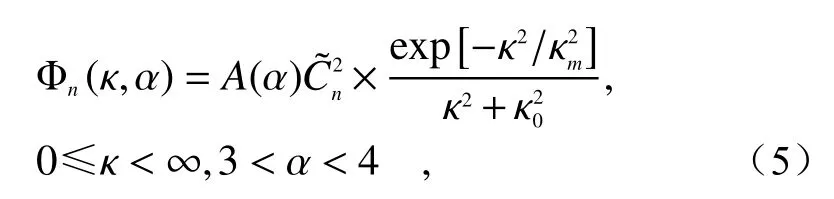
式中, α为功率指数, κ0=2π/L0, κm=c(α)/l0,L0和l0分别代表湍流外尺度和湍流内尺度,为广义折射率结构常数,单位是c(α)=[2πΓ(5−α/2)A(α)/3]1/(α−5),这 里Γ(·)表示Gamma函数。
将式(4)和式(5)代入式(3)可得到:
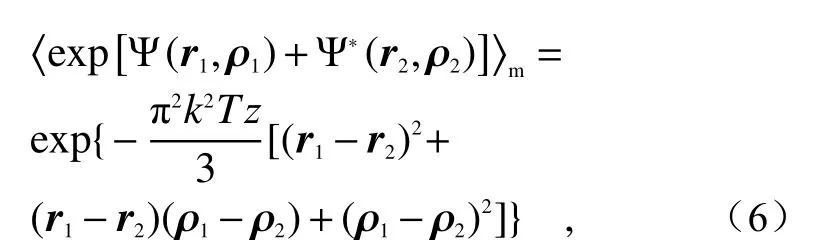
将式(6)代入式(2),做一系列积分之后,可得到扭曲拉盖尔—高斯关联光束在传输距离为z处的交叉谱密度函数:
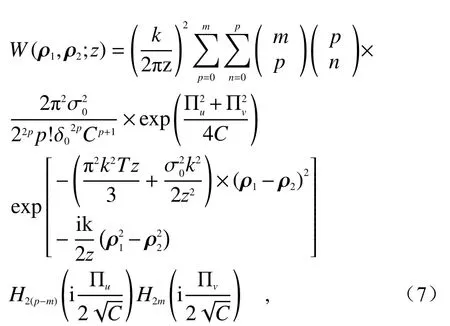
式中,Hm(·)是 m阶数的厄米 多 项 式,
2.3 光束质量因子
光束质量M2因子是评价光束在大气湍流中的传输质量的一个重要指标,下面从Wigner分布函数的二阶矩阵出发,计算扭曲拉盖尔—高斯关联光束的M2因子。为了简便计算,采取坐标代换: ρs=(ρ1+ρ2)/2和 ρd=ρ1−ρ2,则式(2)可写成和差化的形式:
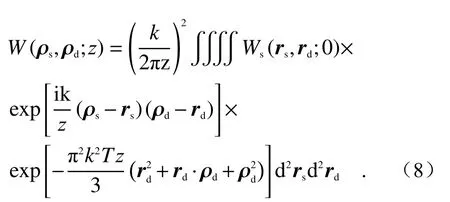
结合文献[23]提出的运算方法,令rs=r′s=和,则上式可以表示为:
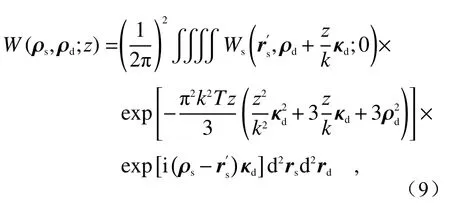
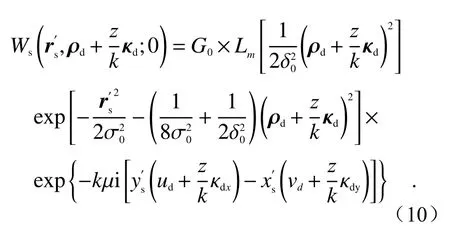
部分相干光的Wigner分布函数可通过对交叉谱密度方程进行二维傅立叶变换得到,即:


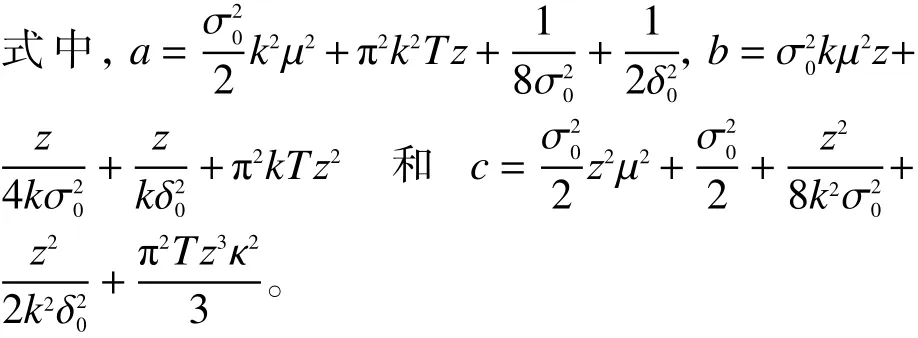
部分相干光Wigner分布函数的n1+n2+m1+m2阶矩阵定义为[24-25]:
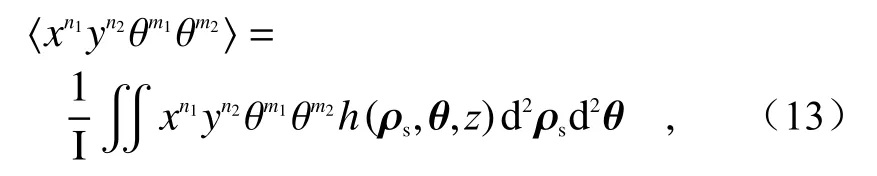
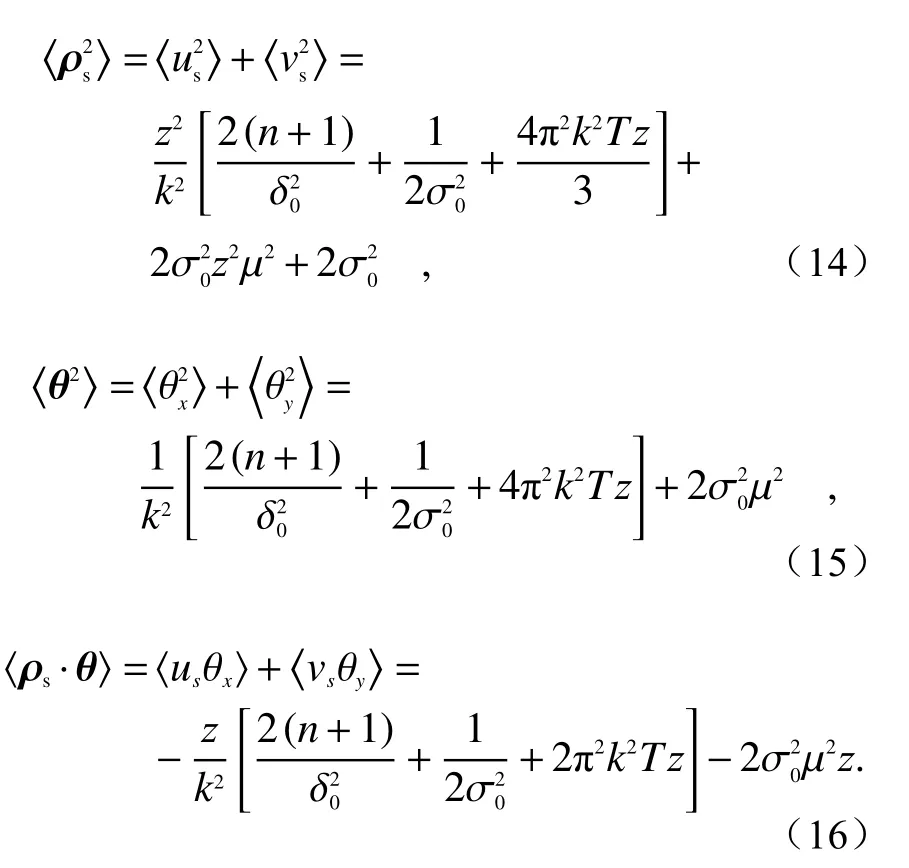
部分相干光束在大气湍流传播后的M2因子用二阶矩定义为[25]:
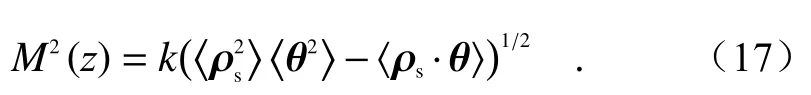
将式(14)、式(15)、式(16)代入到式(17),得到扭曲拉盖尔—高斯关联光束在大气湍流传播后的M2因子为:
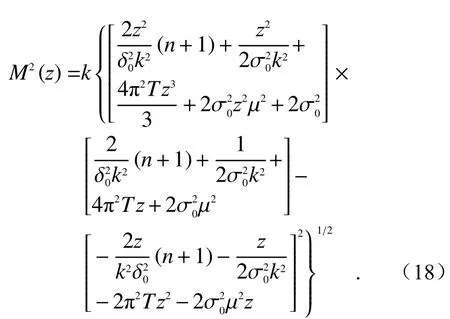
3 数值计算与结果分析10−14m3−a,l0=1mm,L0=1m 。
根据部分相干光理论,光束到达接收面处的平均光强定义为I(ρ)=W(ρ1,ρ2)。结合上述定义,可研究扭曲拉盖尔—高斯关联光束在大气湍流传输中的平均光强分布特性。当光束和大气的参数没有特定给出时,选取如下:λ =632.8nm,σ0=2cm,µ=0.5km−1, δ0=5mm ,m=2,α=3.3,=2.5×
扭曲拉盖尔—高斯关联光束在不同传输距离下的平均光强分布曲线如图2所示。该光束在接近源平面处的平均光强呈高斯分布,随着距离的逐渐增加光束出现了空心的现象,这是由于光源的初始相干结构与远场强度之间存在着互易关系。当传输距离进一步增加时,光束的平均光强受到大气湍流的影响将会逐步退化为高斯分布。此外,扭曲拉盖尔—高斯光束的阶数m会影响平均光强分布随距离变化的速度。当m= 0时,扭曲拉盖尔—高斯关联光束将会退化为扭曲高斯谢尔模光束。阶数m越高,光强分布趋势越平缓,说明高阶光束对大气湍流的抑制作用更强。
为了分析光束和大气参数对湍流抑制作用的影响,图3给出了光束在z=5km处平均光强分布受功率指数α、湍流外尺度L0和湍流内尺度l0、扭曲因子µ 及横截面相干度 δ0的影响情况。图3(a)、3(b)显示了大气参数对光束传输的影响,当功率指数 α和湍流内尺度l0越小,或湍流外尺度L0越大时,光强分布转换为空心分布越快。这说明湍流越强,光强分布变化趋势越明显,这与文献[19]的结论相一致,同时验证了本文数值计算的有效性。图3(c)、3(d)显示了光束参数对大气湍流的抑制作用。当增大扭曲因子µ,或降低横截面相干度 δ0时,会减慢光强分布转化为空心分布的过程,说明大气湍流环境对光强分布的影响将会受到抑制。
图4给出了扭曲拉盖尔—高斯关联光束的归一化M2因子随光束和大气参数变化的情况,M2因子越小说明光束质量越好。从图4(a)、4(c)、4(d)可以发现,阶数m越高的光束,其M2因子的变化趋势更缓慢,受到湍流的影响也更小。如图4(a)所示,归一化M2因子随功率指数α 呈先急速增加后缓慢减小的趋势,在 α=3.11附近取得最大值。这是因为在 α=3.11附近处大气湍流强度最大,光束所受的影响也最大。从图4(b)中可以看出,在大气湍流中,随着传输距离的增加光束质量将下降,但增大湍流内尺度l0或减小湍流外尺度L0都能使M2因子的增加变得缓慢,即减弱大气湍流带来的影响。此外,增加湍流内尺度l0相较于降低湍流外尺度L0,对抑制大气湍流的作用更为明显。从图4(c)、4(d)中不难发现,扭曲因子的增加和相干度的降低都可以减小M2因子,光束传输质量的劣化也随之降低,这与前文的分析相一致。
4 结 论
基于拓展的惠更斯-菲涅尔原理和Wigner函数分布,研究了扭曲拉盖尔—高斯关联光束对大气湍流所带来的负面影响的抑制。通过数值模拟发现,适当增加激光光束的扭曲因子或降低初始光场的相干度都可以有效减小湍流对激光光束传输质量的负面影响。对于扭曲拉盖尔—高斯关联光束来说,光束传输质量同时受到光束参数和大气湍流参数的共同作用。高阶数、相对较大的扭曲因子、低相干度的扭曲拉盖尔—高斯关联光束在大气湍流中的传输质量更好,而具有较大湍流外尺度和较小湍流内尺度的大气会降低光束的传输质量。本论文的研究结论对激光的大气通信和远距离传输具有一定的理论指导意义。

