偏振激光雷达增益比定标方法对比研究

童奕澄，童学东，张 凯，肖 达，戎宇航，周雨迪,3，刘 崇，刘 东

（1. 浙江大学 光电科学与工程学院 现代光学仪器国家重点实验室，浙江 杭州 310027；2. 宁波钢铁有限公司 浙江 宁波 315807；3. 浙江大学 宁波研究院 浙江 宁波 315100）

1 Introduction

Polarization lidar is one of the earliest members of lidar family. Since its birth in 1971, polarization lidar has become a research tool widely used in atmospheric cloud and aerosol detection[1]. The depolarization ratio obtained by polarization lidar inversion can be used to distinguish spherical and non-spherical particles, so it is often applied to the identification of aerosol type and the identification of thermodynamic phase state of clouds[2].Moreover, the depolarization ratio can also be used to identify the tropospheric boundary layer and to distinguish polar stratospheric clouds from other types of clouds in terms of morphology[3-5]. At the same time, the depolarization ratio can be used to study the long-distance transmission characteristics of dust[6]. It can be seen that the high-precision detection of depolarization ratio is of great significance to atmospheric science research. However,how to improve the detection accuracy of depolarization ratio has always been the research focus of polarization lidar[7].

The main causes for depolarization ratio error include: the calibration error of polarization lidar gain ratio, the error caused by the impurity of laser ray polarization, the alignment angle error between laser polarization vector and Polarization Beam Splitter (PBS) incidence plane, as well as the polarization crosstalk error caused when the reflectance and transmittance of PBS cannot reach 100%. In order to simplify the description, the above four errors are referred to as gain ratio calibration error,linear polarization error, alignment angle error and polarization crosstalk error respectively. Among them, gain ratio calibration error is particularly important and has a decisive effect on the accuracy of depolarization ratio[8]. The gain ratio calibration error varies with the gain ratio calibration method. For nearly half a century, more and more researchers have proposed new gain ratio calibration methods.However, there is still a lack of effective guidance and suggestions on the selection of gain ratio calibration method in the actual use of polarization lidar.

This paper analyzes the basic principles of various existing gain ratio calibration methods and compares the accuracy and advantages and disadvantages of +45° method, +45° method, ∆45° method, rotation fitting method and pseudo-depolarizer method at different misalignment angles through experiments. Through the comparison of theory and experiment, this paper provides a suggestion for the best choice of gain ratio calibration method.

2 Basic principles and structure

The typical polarization lidar is a two-channel lidar[1]. According to the definition of depolarization ratio δ[9], we can obtain

where β represents atmospheric backscattering coefficient,Prepresents the echo signal power, and the subscripts ⊥ and ‖ respectively represent the vertical and parallel components of the above parameters.

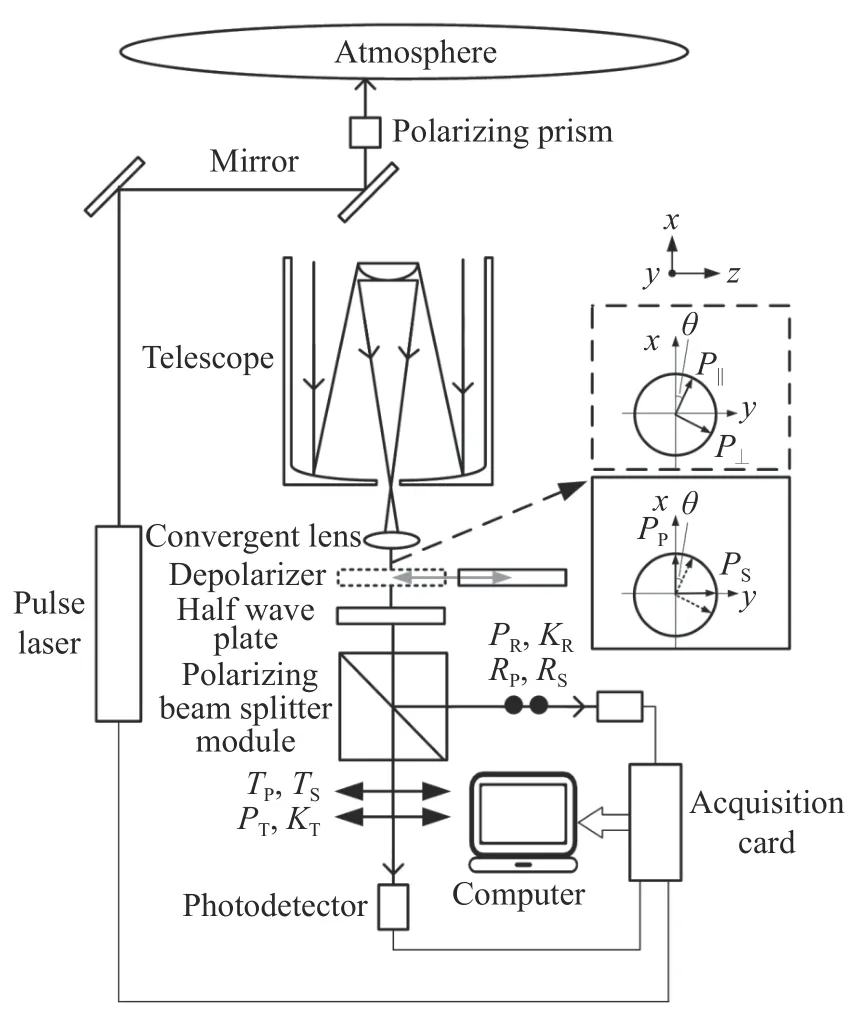
Fig. 1 Basic principle and structure diagram of polarization lidar system图1 偏振激光雷达系统基本原理与结构图

As shown in Fig. 1. the vertical componentP⊥and parallel componentP‖of echo signal can be decomposed into the following components after the coordinate rotation transformation relative to the incident plane of PBS:

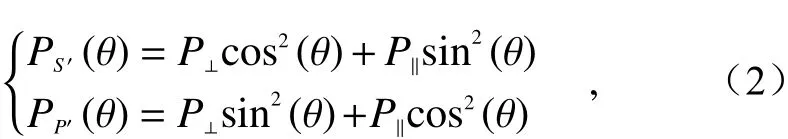
where the subscriptsS′andP′respectively represent the directions perpendicular to and parallel to the incident plane of PBS, andθrepresents the angle between the laser polarization vector and the incident plane of PBS (here referred to as misalignment angle).

Because there is polarization crosstalk in the actual PBS, the parametersRP,RS,TPandTSrespectively represent the reflectance and transmittance ratios of P and S light in PBS (the above four parameters are generally known, and are labeled by PBS manufacturer). After the light passes through the PBS, the detected powerPRandPTin the reflection channel and transmission channel can be expressed as

whereKRandKTrespectively represent the gain coefficients of reflection channel and transmission channel,G=KR/KT. According to the Eq. (3), the actually measured depolarization ratio δ∗(θ) can be obtained:

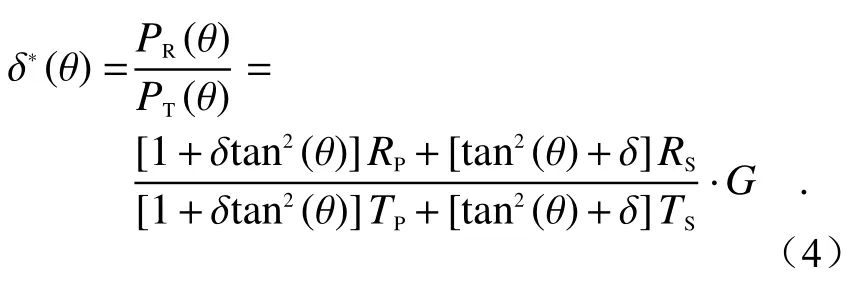
It can be seen from the equations (1) ～ (4) that the gain ratioGmust be calibrated before the calculation of the depolarization ratio, and that the gain ratio calibration error will affect the calculation result of the depolarization ratio[10]. Next, we will introduce several typical gain-ratio calibration methods.

3 Gain ratio calibration methods

3.1 Method of clean atmospheric molecule

The method of clean atmospheric molecule is a method to calibrate the gain ratio by comparing the actual depolarization ratio of clean atmosphere detected by the system and the theoretical depolarization ratio of clean atmosphere, assuming that only atmospheric molecules (no aerosols and clouds) exist in the high air. The calculation formula of depolarization ratio in the method of clean atmospheric molecule is

where δ∗and δ respectively represent the atmo

molspheric molecular depolarization ratio actually measured at the altitudercand the theoretical atmospheric molecular depolarization ratio. δmolcan be calculated according to the theory of atmospheric scattering[11], but it is not fixed. Atmospheric molecular scattering is mainly composed of Rayleigh scattering and vibration Raman scattering (with a negligible intensity). Rayleigh scattering is mainly composed of pure rotational Raman line and central Cabannes line[12]. In the Rayleigh scattering spectrum, Cabannes lines constitute the central peak of Doppler broadening, while pure rotational Raman lines are distributed on both sides of Cabannes lines to constitute the sidebands[13]. The depolarization effect caused by pure rotational Raman lines is much greater than that caused by Cabannes lines. For a li dar system, the value range of δmolis between 0.003 63～0.014 3 when the filters with different bandwidths (BWs) are used[10]. If the filter bandwidth in the lidar system is narrow (BW＜0.3 nm@532 nm), δmolwill be the lower limit, namely δmol=0.003 63. Conversely, if the filter bandwidth is wide (BW=15 nm@532 nm), δmolwill be the upper limit, namely δmol=0.014 3.

Due to convenient operation and no need to add other devices to the light path of the system, the method of clean atmospheric molecule was widely used in the 1980s and 1990s. However, its shortcoming is also very obvious. Because clean atmosphere rarely exists, the calibration result obtained from a calibration area with aerosols or clouds present will have a large error. Moreover, when the filter bandwidth ranges from 1 nm to 15 nm, the proportion of pure rotational Raman lines in the scattered atmospheric molecules cannot be accurately evaluated. This may lead to the inaccurate calculation of the theoretical depolarization ratio of clean atmosphere, resulting in a calibration error. In addition, it should be noted that the method of clean atmospheric molecule is generally applicable to the lidar with a laser wavelength of less than 550 nm.For the lidar with a detection wavelength of more than 800 nm, this calibration method is likely to cause a large calibration error because the Rayleigh scattering intensity is weak[13]. Therefore, this method is rarely used at present.

3.2 +45° method

+45° method is a method of placing a Half-Wave Plate (HWP) in the receiving optical path(generally in front of PBS) and rotating it in one direction (clockwise/counterclockwise) to realize the gain ratio calibration. In particular, this method assumes that the properties of HWP are ideal and that the atmospheric state does not change during calibration. In addition to the above two basic assumptions, two more assumptions should be added to the+45° method, that is, neither a misalignment angle nor polarization crosstalk will exist[14].

As shown in Fig. 2 (Color online), the HWP is placed in the upstream optical path of PBS. In this case, the laser polarization vector is considered to be parallel to the incident plane of PBS, as shown in Fig. 2(a).

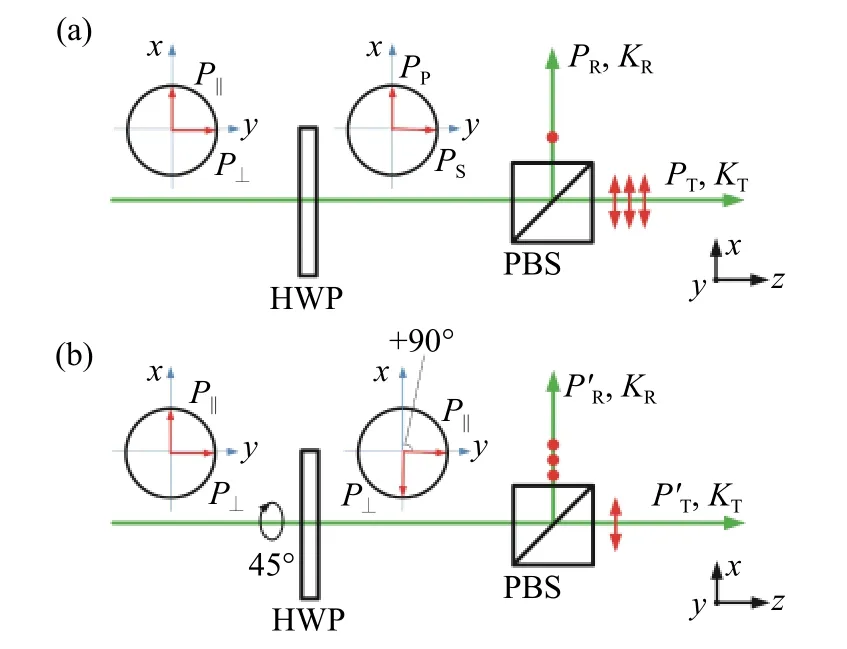
Fig. 2 Schematic diagram of +45° method. (a) Before HWP rotation. (b) After HWP rotation by +45°图2 +45°法原理图。(a)半波片旋转之前；(b)半波片旋转+45°之后

Since the impact of misalignment angle and polarization crosstalk is not considered, the Eq. (3)can be simplified as

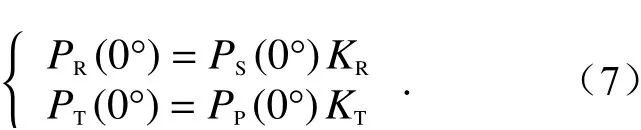
Then, the HWP is rotated clockwise around the optical axis (similar to the counterclockwise case),so the angle between the laser polarization vector and the incident plane of PBS is +90°, as shown in Fi g. 2(b). In the Eq. (7),PT(0°) becomes(90°).The specific formula is not repeated here. In this case, the gain ratioGcan be expressed as

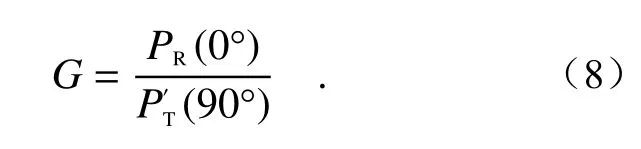
The advantage of this method is easy operation.Its disadvantage is that the alignment angle error and polarization crosstalk error can be easily introduced as the effects of misalignment angle and polarization crosstalk are ignored.

3.3 ±45° method

±45° method is a method of placing a HWP in the receiving optical path and rotating it twice (by+22.5° and −22.5° respectively relative to the initial position) to realize the gain ratio calibration. This method was proposed by Freudenthaleret al. from the University of Munich, Germany[15]. Based on the+45° method, the ±45° method has considered the effects of both misalignment angle and polarization crosstalk. As shown in Fig. 3 (Color online).

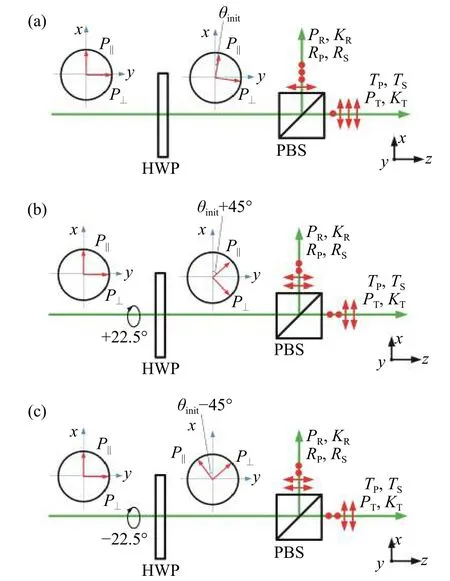
Fig. 3 Schematic diagram of ±45° method. (a) Before HWP rotation. (b) After HWP rotation by +22.5°.(c) After HWP rotation by −22.5°图3 ±45°法原理图。(a)半波片旋转之前；(b)半波片旋转+22.5°之后；(c)半波片旋转−22.5°之后

In Fig. 3, a HWP is placed in the upstream optical path of PBS. It is assumed that there is an initial misalignment angle θinitbetween the laser polarization vector and the incident surface of PBS, and that θhis the quantitative misalignment angle introduced artificially.

After the HWP rotation, the following equation can be derived from Eq. (4):

In order to reduce the influence of initial misalignment angle θinit, the HWP is rotated twice continuously in the ±45° method. At first, the HWP is rotated by +22.5° clockwise around the optical axis relative to its initial position. Then, the HWP is rotated by −45° counterclockwise around the optical axis based on the first rotation, or by −22.5° counterclockwise around the optical axis relative to its initial position. In the two rotations, the angles between the laser polarization vector and the incident surface of PBS are +45° and −45° respectively.At this time, the gain ratioGcan be expressed as

It can be seen from Eq. (10) that in the ±45°method, the polarization crosstalk error of PBS is considered, but the influence of alignment angle error cannot be completely eliminated. It is proved by facts that the error source has little to do with the Signal-to-Noise Ratio (SNR) in the ±45° method[16].If θinit= 1°, the relative error ofGcan be controlled within 5%[15]. With the advantages of simple operation and high accuracy, the ±45° method has been used in MULIS (Multichannel Lidar System), POLIS (Portable Lidar System) and other high-precision polarization lidar systems for gain ratio calibration[16]. Its shortcoming is that the alignment angle error cannot be eliminated.

3.4 ∆45° method

∆45° method is a method of placing a HWP in the receiving optical path and rotating it by 45° in one direction (clockwise/counterclockwise) to realize the gain ratio calibration. This method has the same operation as +45° method, but different calculation approach. In addition, it doesn’t need initial 0° search. This method was proposed by Luo Jinget al. from Zhejiang University[17], as shown in Fig. 4(Color online).

Fig. 4 Schematic diagram of ∆45° method. (a) Before HWP rotation. (b) After HWP rotation by 45°图4 ∆45°法原理图。(a)半波片旋转之前；(b)半波片旋转45°之后

In Fig. 4, a HWP is placed in the upstream optical path of PBS. It is assumed that there is an initial misalignment angle between the laser polarization vector and the incident surface of PBS.

Before the HWP rotation, the following equation can be derived from Eq. (4):

Then, the HWP is rotated around the optical axis, as shown in Fig. 4(b). After rotation, the termsPR(θinit) andPT(θinit) in Eq. (11) turn intoand. The specific formula is not repeated here. In this case, the gain ratio can be expressed as

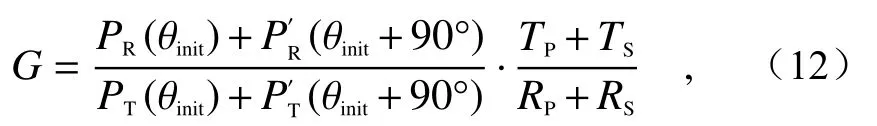
3.5 Rotation fitting method

Rotation fitting method is a method of placing a HWP in the receiving optical path and rotating it for several times to realize the gain ratio calibration through the nonlinear least square fitting and the inversion of gain ratio, depolarization ratio and initial misalignment angle θinit[18]. This method was proposed by Alvarezet al. from NASA.

As shown in Fig. 5 (Color online), a HWP is placed in the upstream optical path of PBS. It is assumed that there is an initial misalignment angleθinitbetween the laser polarization vector and the incident surface of PBS.

If the HWP is rotated artificially by θh,j/2 relative to its initial optical axis, a series of misalignment angles θh,jcan be introduced artificially and quantitatively. From Eq. (9), the following equation can be derived:

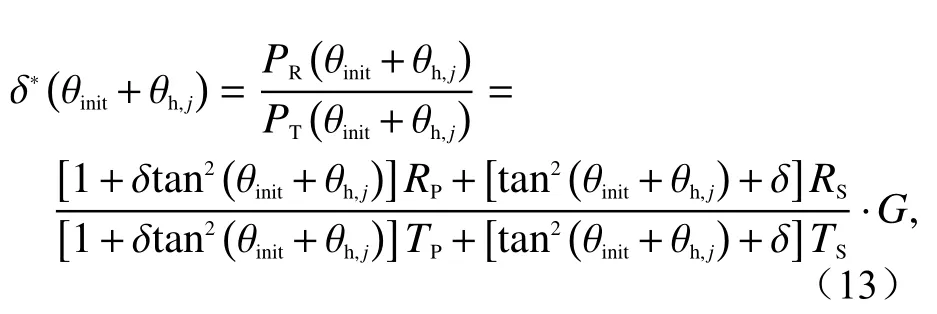
wherejrepresents thej-th rotation of the HWP. In the Eq. (13), asandTScan be considered as known quantities, only three quantities, namely gain ratioG, initial misalignment angle θinitand theoretical depolarization ratio δ, are unknown. In this case, the three unknowns cannot be solved by a single equation. However, multiple equations can be obtained by rotating the HWP for many times. Then the nonlinear least square method can be used to solve the equation set so as to solve the three unknowns. It should be noted that at least three equations need to be obtained in this method, namelyj≥3.

The advantage of this method is that the three unknowns, namely gain ratio, depolarization ratio and initial misalignment angle, can be inverted simultaneously through one calibration, and no a priori value is required. However, due to time-consuming calibration and complicated operation, this method is only suitable for a relatively stable atmospheric environment.

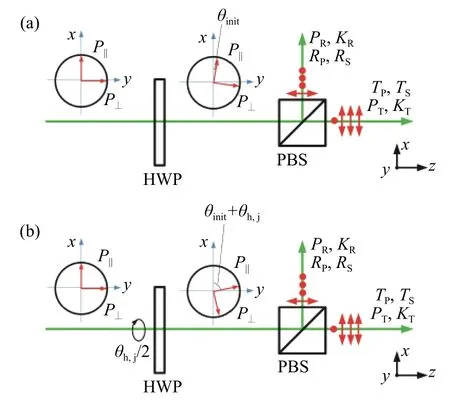
Fig. 5 Schematic diagram of rotation fitting method. (a)Before HWP rotation. (b) After HWP rotation by θh,j图5 旋转拟合法原理图。(a)半波片旋转之前；(b)半波片旋转θ h,j角之后

3.6 Pseudo-depolarizer method

The pseudo-depolarizer method is a method that adds an optical element to the optical path to convert the echo signal received by the system into unpolarized light so as to realize the gain ratio calibration. The gain ratio is calibrated by using the ratio of signal intensities of two detection channels. From Eq. (4), the gain ratioGcan be obtained:

A typical example is found in the CALIOP,where the non-depolarizing signal generated by a depolarizer is used for gain ratio calibration[19]. The specific operation procedure is as follows. A movable depolarizer is placed in the upstream optical path of PBS during the system calibration, and is removed after the calibration completion, as shown in Fig. 6. In the CALIOP, this method is used to calibrate the gain ratio of the system on orbit at night and then the method of clean atmospheric molecule is used to verify the calibration result[20].

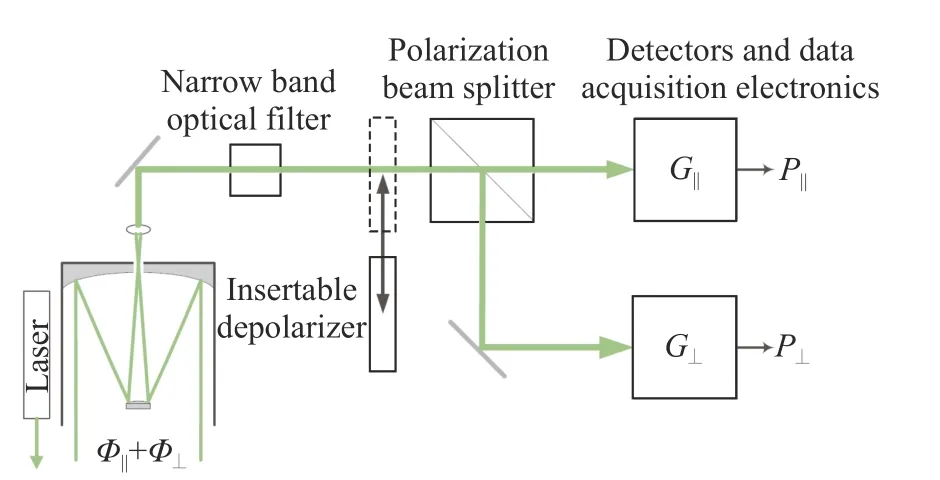
Fig. 6 Schematic diagram for CALIOP gain ratio calibration图6 CALIOP增益比定标原理图

The advantage of this method is that it can be operated easily and calibrated in real time, so as to eliminate the influence of atmospheric state change.Its disadvantage is that other errors will be introduced easily due to the difficulty for a commercial depolarizer to produce completely depolarized light.

4 Experimental results and analysis

The polarization lidar used in the experiment is a typical dual-channel lidar, whose structure is shown in Fig. 1 (where the same device is only marked once). The pseudo-depolarizer between the convergent lens and the HWP is only used in the pseudo-depolarizer method. To reduce linear polarization error, a polarizing prism was added to the emergent light path in the experiment system, so that the extinction ratio of the outgoing laser reached 2×105∶1. To reduce the polarization crosstalk error, a PBS was glued with a polarizing film to achieveTP:TS(RS:RP)>30 000∶1. Therefore, the effect of alignment error on gain ratio is discussed instead of the effect of linear polarization error and polarization crosstalk error. The specific parameters of the system are shown in Table 1.

Tab. 1 Main parameters for polarization lidar system表1 偏振激光雷达系统主要参数

Due to the large calibration error of clean atmospheric molecules, the experiment in this paper mainly compares the influence of five methods,namely, +45° method, ±45° method, ∆45° method,rotation fitting method and pseudo-depolarizer method, on the gain ratio calibration at different misalignment angles (alignment angle errors).

To ensure a high signal-to-noise ratio, the experiment was carried out at night. Meanwhile, in order to reduce the impact caused by atmospheric changes, the detection in horizontal direction (pitch angle: 0°) was adopted. After the optical axis calibration of the system was completed, an electric rotating motor (accuracy: 0.005°) was used to adjust the half-wave plate to the position where the laser polarization vector was parallel to the incident surface of PBS (when 200 signals on average were passed and the maximum power of transmission channel was detected visually). At this point, the HWP angle was the initial 0°. It should be noted that, for the convenience of description, the initial misalignment angle θinitis not included in the actual total misalignment angle when the misalignment angle θhis introduced artificially and quantitatively to the following section. However, each actual misalignment angle contains the initial misalignment angle θinit(an unknown quantity). Then, withθh=0°(the actual misalignment angle is θinit+0°) as the zero point, an electric rotating motor is used to rotate the HWP. In the actual operation, the alignment angle usually does not exceed 15°[21-22]. However, to ensure the experiment integrity, the misalignment angle under discussion is expanded to 45° in this paper.

In the +45° method, ±45° method, ∆45° method and rotation fitting method, the HWP was rotated with a step size of 2.5° within the θhrange of−45°～67.5° to obtain a total of 46 sets of original echo signals. By processing the above data, a step size of 5° and a θhrange of −45° ～ +45° (that is, the difference between the two angles in each group of data before and after the HWP rotation are 45°)were selected in the four methods. After calculation,a total of 19 groups of gain ratio data were obtained.

Before starting the experiment, a pseudo-depolarizer was added to the optical path of the system, as shown in Fig. 1. Since the pseudo-depolarizer was not ideal, the HWP was rotated with a step size of 10° within the θhrange of −80°∼+100° to obtain a total of 19 sets of original echo signals in order to observe the change of pseudo-depolarizer in at least one cycle. By processing the above data, a total of 19 groups of gain ratio data were obtained after calculation.

The calibration results of the above five methods are given in Table 2 (θh=0 °).

Tab. 2 Calibration results of five methods atθh=0◦表2 θh=0◦时5种方法的定标结果

As can be seen from Table 2, when there is no misalignment angle (θh=0 °), the calibration results of±45° method, ∆45° method and rotation fitting method are close to each other and can be considered closest to the true value. Therefore, the average value of the gain ratios measured by the above three methods at θh=0 ° is defined as the true value.The curves of the relative errors of the five calibration methods changing with the misalignment angle are shown in Fig. 7 (the calculation processes of rotation fitting method and pseudo-deflector method are described in detail in the Sections 4.2 and 4.3).

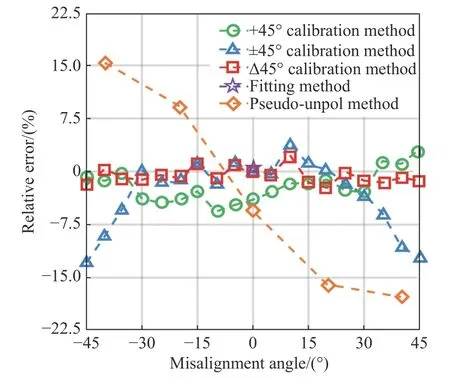
Fig. 7 Relative errors changing with the misalignment angle for the five calibration methods图7 5种定标方法相对误差随对准偏失角的变化曲线

4.1 +45°, ±45° and ∆45° methods

As shown in Fig. 7, when |θh|＜15°, the calibration results of ±45° method and ∆45° method are similar with a small relative error. However, even if the misalignment angle is 0°, the calibration result of +45° method is still greatly different from those of the above two methods, with a relative error up to 4%. When |θh|>15°, the calibration results of +45°method and ∆45° method will remain almost stable.However, with the increase of misalignment angle,the calibration result of ±45° method will become more unstable and its relative error will increase sharply even up to 12.93%. The main reason for such error distribution is that the ±45° method calculates the geometric average of the two measurements before and after rotation, while the ∆45°method calculates the arithmetic average of the two measurements before and after rotation based on the+45° method. The reasons for the above phenomena of +45° method will be explained below through specific theoretical analysis.

The relative error between the two methods was analyzed[23-24]. The powers detected in the reflection channel and transmission channel before and after the HWP rotation in the two methods are denoted asand. Then

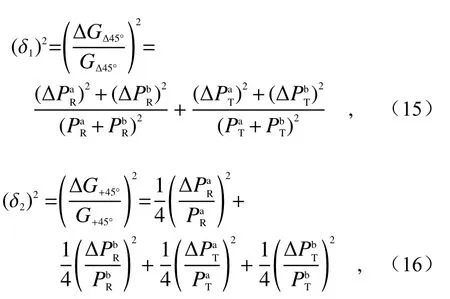
where δ1and δ2represent the relative errors of the calibration results of ∆45° method and ±45° method,and(SisRorTandnisaorb) represents the uncertainty (standard deviation) in each measured value. The photon counting signal in lidar can be considered to be subject to Poisson distribution[25-26],so the statistical error is equal to the root mean square of the mean value of the signal, i.e.Therefore, the equations (15) and (16) can be further deduced as follows

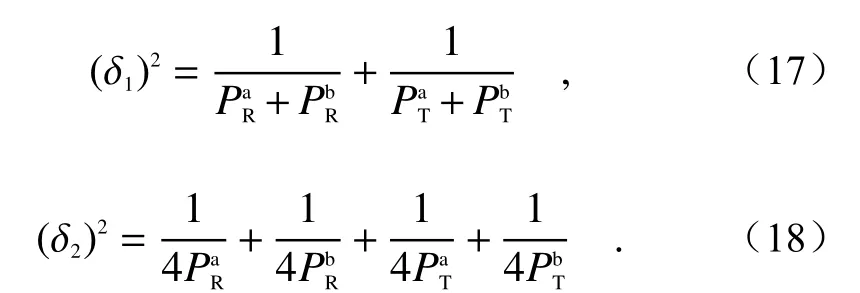
4.2 Rotation fitting method

Considering that the error of misalignment angle was not greater than 15° in the actual process,13 sets of data satisfying |θh|≤ 15° (that is, θh,j= 0°,±2.5°, ±5° ··· ±15°) were selected for fitting. The calculation results of rotation fitting are shown in Fig. 8 (Color online). According to Eq. (13), solving the three unknowns (gain ratioG, initial misalignment angle θinitand theoretical depolarization ratio δ) in the equations is a nonlinear least square problem. Before solvingG, θinitand δ, their initial values need to be predicted. Their optimum initial predicted values are shown in Fig. 8.

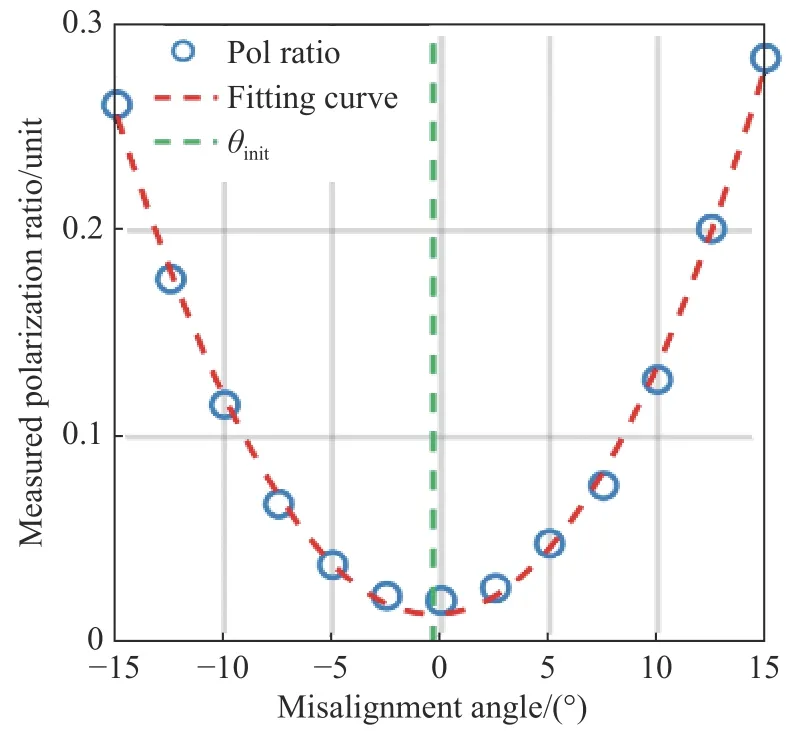
Fig. 8 Curve of the actually measured depolarization ratio changing with the misalignment angle, where the blue circle represents the δ∗(θ) values measured at different θ angles, and the red and green dotted lines represent the fitting curve and θ init, respectively图8 实际测量退偏比随对准偏失角的变化曲线图。其中蓝色圆圈代表在不同θ 情况下测量的 δ∗(θ)，红色虚线代表拟合曲线，绿色虚线代表θinit

It can be found that the relationship betweenand θh,j(blue circle) can be approximately represented by a quadratic polynomial[27].Therefore, the following quadratic polynomial is constructed with the artificially and quantitatively introduced misalignment angle θh,jas an independent variable and the actually measured depolarization ratioas a dependent variable:

whereA0,A1andA2are quadratic polynomial coeffici ents. The fitting result is shown as the red dotted line in Fig. 8. The minimum value of the quadratic polynomial represents the initial misalignment angle θinit, whose result is calculated to beθinit=−A1/(2×A2)= −0.35°. This value can be used as the optimum initial predicted value of θinit. Then, θinit=−0.35° is substituted into Eq. (13) and the equation set is solved with nonlinear least square method to obtain the gain ratio, namelyG=1.2716.

4.3 Pseudo-depolarizer method

The calculation result of pseudo-depolarizer method is shown in Fig. 9 (Color online), in which the blue circles represent the gain ratios calculated at different angles of the HWP. It can be observed that the distribution of blue circles is in line with the cosine curve distribution law. Therefore, the following cosine function polynomial is constructed with the HWP rotation angle φ (θh=2φ) as an independent variable and the gain ratioGas a dependent variable:

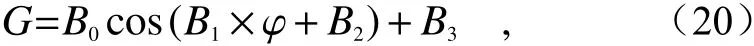
whereB0,B1,B2andB3all represent the coefficients of the cosine function polynomial. The fitting result is shown as the red dotted line in Fig. 9.

Theoretically, if the echo signal is completely unpolarized light, its state will remain unchanged,irrespective of how the HWP angle is changed. In other words, the rotation of HWP will not affect the value of gain ratio. The result of gain ratio calibration should be represented by a line parallel to thexaxis, rather than by a cosine curve as shown in Fig. 9. The reason for this problem is that the existing commercial depolarizer cannot completely transform the polarized light into unpolarized light, so that the echo signal still contains part of the polarized light after passing through the depolarizer.When using laser as the light source to test the depolarizing effect of a depolarizer, Luo Jing et al.from Zhejiang University found that the test result was similar to the cosine distribution in Fig. 9[28].This indicates that the result of gain ratio calibration will still be affected by this portion of polarized light even if the misalignment angle is 0°.

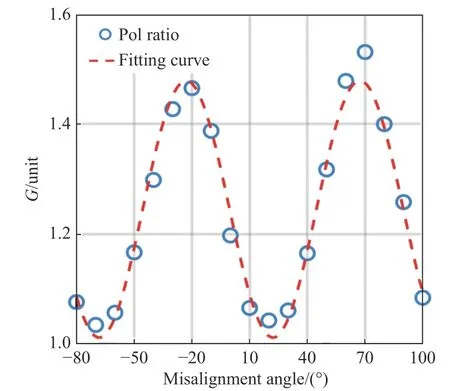
Fig. 9 Gain ratio calibration result of pseudo-depolarizer method. The blue circles represent the gain ratios measured at different misalignment angles, and the red dotted line represents the cosine polynomial fitting curve图9 退偏器法增益比定标结果。蓝色圆圈代表半波片在不同角度下测量的增益比，红色虚线代表余弦函数多项式拟合曲线

It should be noted that among the measurement data obtained by pseudo-depolarizer method,only 5 sets of data satisfy θh= −45° ～ +45°. Therefore, only 5 points are marked in Fig. 7 according to this method. At θh= 0°, the relative error of pseudodepolarizer method is 5.6%. This indicates that the result of gain ratio calibration will still be affected by this portion of polarized light even if the misalignment angle is 0°.

4.4 Discussion

Through the analysis of experimental results,we know that the calibration results of ±45° method,∆45° method and rotation fitting method are the most accurate. This is consistent with the above theoretical analysis result. However, the error of ±45°method will increase with the misalignment angle.The rotation fitting method is only suitable for a relatively stable atmospheric environment due to timeconsuming calibration and complicated operation. In comparison, ∆45° method has obvious advantages:easier operation, robust calibration results not affected by misalignment angle, and no need to search for the initial 0° angle. However, ∆45° method cannot eliminate the influence of atmospheric state changes. In contrast, the pseudo-depolarizer method is not only easy to operate, but also capable of eliminating the influence of atmospheric state changes and free from the problem that multiple HWP rotations will increase the accumulated angle error. But so far, the commercial depolarizer still cannot produce completely depolarized light, which will introduce a new error that is difficult to evaluate. In conclusion, we suggest the use of ∆45° method for calibration as a general rule and the use of pseudo-depolarizer method for calibration when a high-precision depolarizer is available.

5 Conclusion

The calibration accuracy of gain ratio has a great influence on the detection accuracy of polarization lidar. This paper compares a variety of the existing gain-ratio calibration methods theoretically and experimentally for the first time, and provides some suggestions on the selection of gain-ratio calibration methods.

As far as the operability is concerned, the pseudo-depolarizer method only needs a depolarizer inserted into the system to realize the calibration, and can eliminate the influence of atmospheric state changes. The other four methods require at least two rotations of the HWP in relatively complicated operation and cannot eliminate the influence of atmospheric state changes. In terms of calibration accuracy, this experiment mainly compared the influence of +45° method, ±45° method, ∆45°method, rotation fitting method and pseudo-depolarizer method (excluding the method of clean atmospheric molecule due to its large calibration error)on the gain ratio calibration at different misalignment angles. The experimental results show that the calibration accuracy of ±45° method, ∆45° method and rotation fitting method is relatively high, but the operation of ±45° method and rotation fitting method is quite complex. The error of ±45° method is big when the misalignment angle is large. In the ∆45°method, the result of gain ratio calibration is not affected by the misalignment angle, and there is no need to search for the initial 0° angle. Compared with the first three methods, +45° method has a larger error when the misalignment angle is 0°. The pseudo-depolarizer method is greatly affected by the use of non-ideal depolarizer. If an ideal depolarizer is available, this method will be an ideal gain-ratio calibration method. By comparing different gain-ratio calibration methods theoretically and experimentally, this paper gives the best choice of gain ratio calibration method, suggesting the use of ∆45°method for calibration as a general rule and the use of pseudo-depolarizer method for calibration when a high-precision depolarizer is available.

——中文对照版——

1 引 言

偏振激光雷达是激光雷达家族中最早的成员之一，自1971年诞生以来，其已广泛应用于大气云及气溶胶探测[1]。偏振激光雷达反演得到的退偏比可用于区分球形粒子和非球形粒子，故其常被应用于气溶胶的类型识别及云的热力学相态识别[2]。不仅如此，退偏比也可用于识别对流层的边界层以及从形态学上区分极地平流层云与其它种类云[3-5]。同时，退偏比还可以用于研究沙尘的长距离传输特性[6]。可见，实现退偏比的高精度探测对大气科学研究具有重要的意义。然而，如何提高退偏比的探测精度，一直以来都是偏振激光雷达的研究重点[7]。

退偏比误差产生的主要原因包括：偏振激光雷达增益比的定标误差、发射激光线偏振度不纯而引起的误差、激光偏振矢量与偏振分光棱镜（Polarization Beam Splitter，PBS）入射面的对准角误差以及PBS反射、透过率无法达到100%而引起的偏振串扰误差。为了简化描述，本文分别简称上述4种误差为增益比定标误差、线偏振度误差、对准角误差与偏振串扰误差，其中增益比定标误差大小对退偏比的精度起着决定作用[8]。不同增益比定标方法所产生的增益比定标误差也不同。近半个世纪，不断有研究人员提出新的增益比定标方法，然而到目前为止，偏振激光雷达在实际使用过程中对增益比定标方法的选择依旧缺少有效的指导与建议。

本文介绍了现存多种增益比定标方法的基本原理，并通过实验对比分析了+45°法、±45°法、∆45°法、旋转拟合法与退偏器法在不同对准偏失角情况下增益比定标的准确性以及各自的优缺点。通过理论与实验的对比，本文给出了增益比定标方法的最佳选择。

2 基本原理与结构

目前常见的偏振激光雷达为双通道的激光雷达[1]，根据退偏比[9]的定义，可得

式中，β代表大气后向散射系数，P代表回波信号功率，下标 ⊥与 ‖分别代表上述各参量的垂直与平行分量。如图1所示，回波信号垂直分量P⊥与平行分量P‖相对于PBS入射面在经坐标旋转变换后可分解为

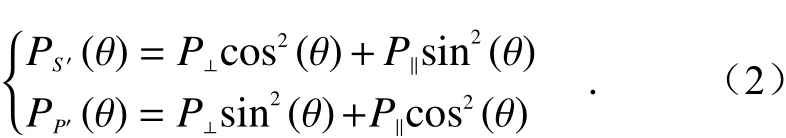
式中，下标S′与P′分别代表与PBS入射面垂直方向及平行方向，θ代表激光偏振矢量与PBS入射面存在的夹角（此处称为对准偏失角）。

由于实际的PBS存在偏振串扰，因此，定义RP、RS、TP与TS分别代表PBS对P光与S光的反射率与透过率（以上4个参数一般由PBS生产商标称出，属于已知量）。经过PBS后反射通道与透射通道被探测到的功率PR、PT分别可表示为

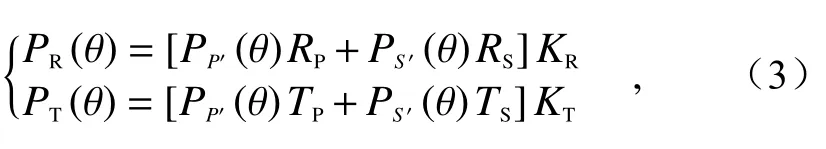
式中KR与KT分别代表反射通道与透射通道的增益系数。其中G=KR/KT，根据式（3）可得实际测量退偏比δ∗(θ)

由式（1）～式（4）可知，在计算退偏比之前必须完成增益比G的定标，而增益比定标的误差会对退偏比的计算结果造成影响[10]。接下来本文将介绍几种常用的增益比定标方法。

3 增益比定标方法

3.1 洁净大气分子法

洁净大气分子法是假定高空中只存在大气分子（无气溶胶与云），通过对比系统探测洁净大气实际退偏比与洁净大气理论退偏比以完成增益比定标的方法。洁净大气分子法退偏比的计算公式为

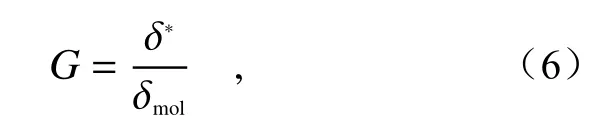
式中，δ∗与 δmol在此处分别代表高度为rc处实际测量大气分子退偏比与理论大气分子的退偏比。δmol可以根据大气散射理论[11]计算得到，但是该理论值并不固定。由于大气分子散射主要由瑞利散射与振动拉曼散射（该散射强度很小，可忽略不计）组成，其中瑞利散射主要由纯转动拉曼线与中心Cabannes线组成[12]。在瑞利散射光谱结构中，Cabannes线属于多普勒展宽的中央峰，纯转动拉曼线分布在Cabannes线的两侧，属于边带[13]，纯转动拉曼线造成的退偏效果比Cabannes线大得多。对于激光雷达系统说，使用不同带宽（Bandwidth，BW）的滤光片， δmol取值范围在0.003 63～0.014 3之间[10]。如果激光雷达系统中滤光片的带宽较窄（BW＜0.3 nm@532 nm）， δmol=0.003 63。反之，如果滤光片的带宽较宽（BW=15 nm@532 nm），则δmol=0.014 3。

洁净大气分子法由于操作比较方便，且不需要在系统光路中添加其它器件，所以该定标方法在上世纪末使用较为广泛，但其缺点也很明显，因为真正洁净的大气很少存在，若选取的定标区域存在气溶胶或云，定标结果将会产生较大误差，而且当滤光片带宽在1～15 nm时，由于无法准确评估纯转动拉曼线在大气分子散射中所占的比例，可能导致洁净大气理论退偏比计算不准确，从而造成定标误差。另外，需要注意的是，洁净大气分子法一般适用于激光波长小于550 nm的激光雷达。对于探测波长大于800 nm的激光雷达，由于瑞利散射强度较小，使用该定标方法易造成较大的定标误差[13]。因此，该方法目前很少被采用。

3.2 + 45°法

+45°法是一种将半波片（Half-Wave Plate，HWP）置于接收光路中（一般置于PBS前），通过单方向（顺/逆时针均可）旋转半波片以完成增益比定标的方法。需要特别说明的是，该方法假设半波片的性质理想，且定标时大气状态不发生改变。对于+45°法，除了以上两个基本假设外，还需要增加另外两个假设，即不存在对准偏失角，也不存在偏振串扰[14]。

如图2（彩图见期刊电子版）所示，首先将半波片放置于PBS上游光路中，此时认为激光偏振矢量与PBS入射面平行，如图2(a)所示。

此时由于不考虑对准偏失角和偏振串扰的影响，式（3）可简化为

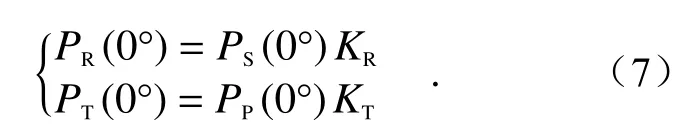
然后将半波片绕光轴顺时针旋转（逆时针类似），使得激光偏振矢量与PBS入射面成+90°，如图2(b)所示，式（7）中的PT( 0°)变为，具体公式不再赘述，此时增益比G可表示为

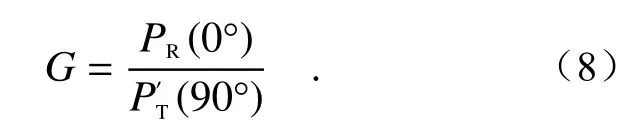
该方法的优点是操作较简便，缺点为忽略了对准偏失角和偏振串扰的影响，易引入对准角误差与偏振串扰误差。

3.3 ±45°法

±45°法是一种将半波片置于接收光路中，通过旋转两次半波片（相对于初始位置，分别旋转+22.5°与 − 22.5°）以完成增益比定标的方法。该方法由德国慕尼黑大学的Freudenthaler等人提出[15]。±45°法在+45°法的基础上同时考虑了对准偏失角和偏振串扰的影响。

如图3（彩图见期刊电子版）所示，将一个半波片放置在PBS上游光路中，假设此时激光偏振矢量与PBS入射面存在初始对准偏失角 θinit，θh为人为定量引入的对准偏失角。

半波片旋转之后，由式（4）可得

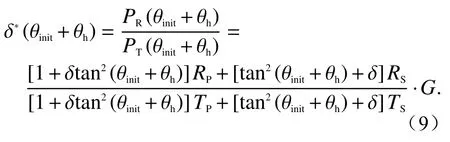
为了减小初始对准偏失角 θinit的影响，±45°法采用连续两次旋转半波片的方式，第一次使半波片相对于初始位置绕光轴顺时针旋转+22.5°，第二次在第一次旋转的基础上使半波片绕光轴逆时针旋转−45°，即相对于初始位置绕光轴逆时针旋转−22.5°，分别使得激光偏振矢量与PBS入射面成+45°与−45°，此时增益比G可表示为

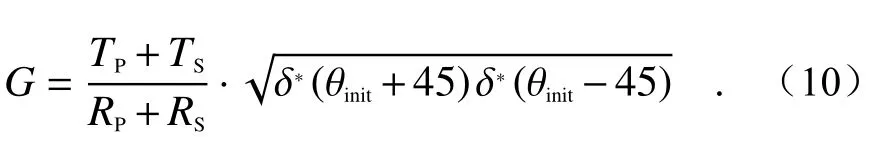
由式（10）可以看出，±45°法虽然考虑了PBS偏振串扰误差，但无法完全消除对准角误差的影响。事实证明，±45°法的误差来源与信噪比关系不大[16]，当 θinit= 1°时，G的相对误差可以控制在5%以内[15]。由于±45°法操作较为简便且精度较高，目前已经被MULIS（Multichannel Lidar System）、POLIS（Portable Lidar System）等高精度偏振激光雷达系统用于增益比的定标[16]。其缺点为无法消除对准角误差。

3.4 ∆45°法

∆45°法是一种将半波片置于接收光路中，通过单方向（顺/逆时针均可）旋转45°半波片以完成增益比定标的方法（其与+45°法的操作方法一样，但计算方式不同，且无需进行初始0°角搜寻）。该方法由浙江大学罗敬等人提出[17]。

如图4所示，将一个半波片置于PBS的上游光路中，假设此时激光偏振矢量与PBS入射面存在初始对准偏失角。

半波片旋转之前由式（4）可得

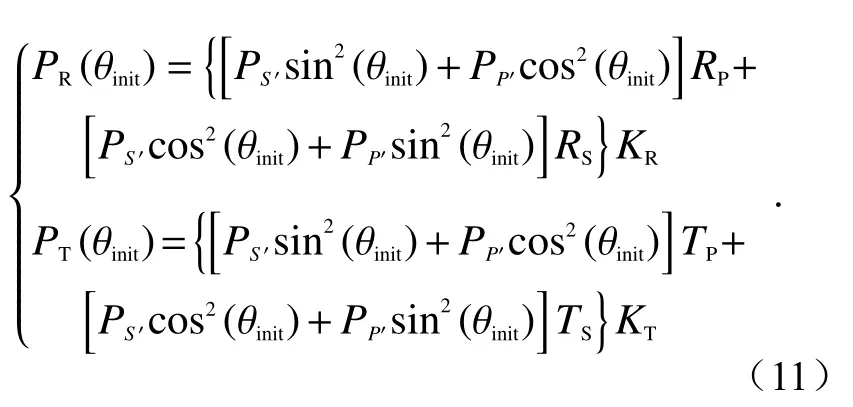
然后将半波片绕光轴旋转，如图4(b)所示，旋 转 之 后 式（11）中 的PR(θinit)与PT(θinit)变 为与，具体公式不再赘述，此时增益比可表示为

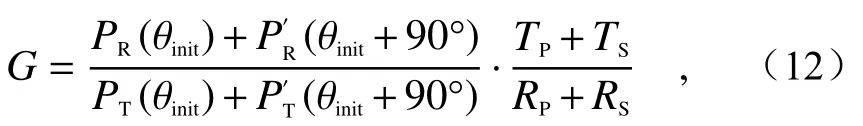
3.5 旋转拟合法

旋转拟合法是一种将半波片置于接收光路中，通过多次旋转半波片，采用非线性最小二乘法拟合同时反演增益比、退偏比以及初始对准偏失角 θinit以完成增益比定标的方法。该方法由美国宇航局的ALVAREZ等人提出[18]。

如图5所示，将一个半波片放置于PBS上游的光路中，假设此时激光偏振矢量与PBS入射面存在初始对准偏失角θinit。

如果人为控制半波片相对于其初始光轴位置旋转 θh,j/2角，可获得一系列由人为定量引入的对准偏失角θh,j。则由式（9）可得

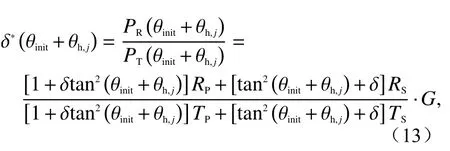
式中，j代表第j次旋转半波片。观察式（13），由于与TS可 认 为 是 已 知 量，那么式（13）中只有3个未知量，即增益比G、初始对准偏失角 θinit以及理论退偏比δ。此时一个方程无法求解3个未知数，但由于多次旋转半波片可得到多个方程，采用非线性最小二乘法对该方程组进行求解，即可解出3个未知数。需要注意的是，该方法要求至少得到3个方程，即j≥3。

该方法的优点为一次定标可同时反演增益比、退偏比以及初始对准偏失角3个未知量，并且不需要知道先验值。其缺点为定标耗时较长，操作繁琐，只适用于相对稳定的大气环境下。

3.6 退偏器法

退偏器法是一种通过在光路中添加光学元件将系统接收的回波信号转换为非偏振光以完成增益比定标的方法。其利用两路探测通道信号强度之比进行定标，由式（4）可求解增益比G

其中较为典型的是CALIOP利用退偏器产生的非退偏光信号来进行增益比定标[19]。具体操作为在PBS上游光路放置一个可移动的退偏器，系统定标时将其置于光路中，定标结束后移出光路，如图6所示。CALIOP采用该方法在夜间轨道上对系统进行增益比定标，并采用洁净大气分子法进行验证[20]。

该方法优点为操作简便并且可进行实时定标，从而排除大气状态改变造成的影响。其缺点为商用退偏器还难以产生完全的退偏光，易引入其它误差。

4 实验结果与分析

实验所采用偏振激光雷达为典型的双通道激光雷达，系统结构如图1所示（图中相同的器件只标注一次）。其中介于会聚透镜与半波片之间的退偏器只有在采用退偏器法定标时才会使用，其它时候不需要使用该光学器件。为了减少线偏振度误差，实验系统在出射光路中添加了起偏棱镜，使得出射激光的消光比达到了 2×105∶1。为了减少偏振串扰误差，实验系统采用PBS与偏振片胶合的结构，使得TP:TS（RS:RP）>30 000∶1。因此，本文暂不讨论线偏振度误差与偏振串扰误差，只讨论对准误差对增益比造成的影响。系统的具体参数如表1所示

由于洁净大气分子法定标误差较大，因此，本文实验主要对比分析了采用+45°法、±45°法、∆45°法、旋转拟合法与退偏器法等5种方法在不同对准偏失角（对准角误差）情况下对增益比定标的影响。

为保证实验有较高的信噪比，实验时间选在夜间。同时，为了减少大气变化而带来影响，选取水平方向（俯仰角为0°）探测。在完成系统光轴校准后，使用电动旋转电机（精度为0.005°）调整半波片到激光偏振矢量与PBS入射面平行的位置（目测透射通道平均信号最大时即为对应位置），此时半波片的角度为0°初始值。需要注意的是，为了表述方便，下文在人为定量引入对准偏失角 θh时 ，未将初始对准偏失角 θinit表示在实际总的对准偏失角中，但实际上每个对准偏失角都包含了初始对准偏失角 θinit（θinit属于未知量）。然后，以 θh=0°（实际对准偏失角为 θinit+0°）作为零点，使用电动旋转电机旋转半波片。一般来说，在实际操作过程中对准偏失角不会超过15°[21-22]，但为了实验的完整性，本文将对准偏失角的讨论扩大至45°。

+45°法、±45°法、∆45°法与旋转拟合法均以2.5°为 间隔旋转半波片得到 θh=−45°～67.5°情况下共46组原始回波信号。通过对上述数据进行处理，+45°法、±45°法、∆45°法与旋转拟合法4种方法均选择5°为间隔，选取 θh的范围为−45° ～ +45°，（即每组数据两个角度在半波片旋转前后相差45°），计算后一共可获得19组增益比数据。

采用退偏器法时，在开始实验之前需要在系统光路中添加退偏器，如图1所示。由于退偏器是非理想的，为了观察其至少一个周期的变化，退偏 器 法 以10°为间隔转半波片得到 θh从−80°到+100°情况下共19组原始回波信号，通过对上述数据进行处理，一共可获得19组增益比数据。

表2是当θh=0 °时，5种方法的定标结果。观察表2可以发现，当没有对准偏失角时，±45°法、∆45°法与旋转拟合法定标结果较为接近，可以认为上述3种方法在θh=0 °时最接近真实值。令上述3种方法在 θh=0°时测得增益比的平均值为真实值，并绘制出如图7所示的5种定标方法的相对误差随对准偏失角的变化曲线（旋转拟合法与退偏器法计算过程详见4.2与4.3节）。

4.1 +45°、±45°、∆45°法

如图7所示，当| θh|＜15°时，±45°法与∆45°法的定标结果相近，相对误差也较小，而+45°即使不存在对准偏失角时，定标结果也与上述两种方法存在较大差异，相对误差可达4%。当 |θh|>15°时，+45°法与∆45°法的定标结果总体保持稳定，而±45°法的定标结果随对准偏失角的增大而变得不稳定，相对误差急剧增大，甚至高达12.93%。±45°法出现这样误差分布的原因主要在于其计算前后两次测量数据的几何平均，而∆45°法则是在+45°法的基础上计算前后两次测量数据的算术平均。下文将通过具体理论分析来解释+45°法出现上述现象的原因。

对两种方法进行相对误差分析[23-24]，令两种方法旋转半波片前后反射通道与透射通道探测到的功率分别为与，可得

式中 δ1与 δ2分别代表∆45°法与±45°法定标结果的相对误差，（S为R,T且n为a,b）代表各个测量值的不确定度（标准差）。激光雷达中光子计数的信号可以认为服从泊松分布[25-26]，因此统计误差等于信号平均值的均方根，即，因此，式（15）与式（16）可进一步推导为与作差可发现，，即∆45°法的不确定度小于等于±45°法。事实上，根据实验结果，±45°法在对准偏失角较大的情况下，定标的增益比廓线的振荡幅度的确要大于∆45°法，这也解释了图7中±45°法在对准偏失角较大的情况下，误差远大于∆45°法的原因。

4.2 旋转拟合法

考虑到实际过程中对准偏失角的误差不会超过15°，选择 |θh|≤ 15°的13组数据（即θh,j=0°, ±2.5°,±5°···±15°）进行数据拟合，旋转拟合法计算结果如图8（彩图见期刊电子版）所示，其中蓝色圆圈代表在不同 θh情 况下的 δ∗(θ)，由式可知，求解增益比G、初始对准偏失角 θinit以及理论退偏比δ 3个未知数的方程组属于非线性最小二乘法问题。求解之前需要对G、θinit与δ 3个未知数的初始值进行预测。为了得到最佳初始预测值，由图8可知，与 θ之间的关系（蓝色圆圈）可以近似h,j用一个二次多项式来表示[27]，故以人为定量引入对准偏失角θh,j为自变量，实际测量退偏比为应变量构建如下二次多项式

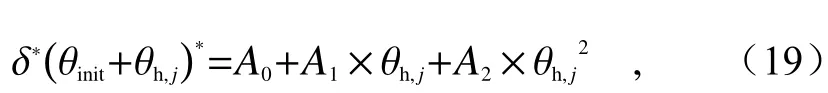
式中，A0、A1与A2均为二次多项式系数。拟合结果如图8中红色虚线所示，该二次多项式的最小值即代表初始对准偏失角 θinit，计算结果θinit=−A1/(2×A2)= −0.35°，该值可作为 θinit的最佳初始预测值。接着，将θinit= −0.35°代入式（13）并使用非线性最小二乘法求解方程组，求得增益比G=1.2716。

4.3 退偏器法

退偏器法计算结果如图9（彩图见期刊电子版）所示，其中蓝色圆圈代表在半波片不同角度下计算的增益比，观察各蓝色圆圈的分布情况，可知其较为符合余弦曲线分布规律。故以半波片旋转角度φ (θh=2φ) 为自变量，增益比G为应变量构建如下余弦函数多项式

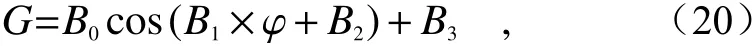
式中，B0、B1、B2与B3均代表余弦函数多项式的系数。拟合的结果如图9中红色虚线所示

从理论上来说，假如回波信号为完全的非偏振光，那么无论如何改变半波片的角度都无法改变非偏振光的状态。换句话说，旋转半波片并不会影响增益比的数值，增益比定标的结果应该表征为一条平行于x轴的直线，而非像图9中那样表现为余弦的分布情况。导致该问题的原因是目前商用退偏器无法将偏振光完全转化为非偏振光，回波信号在经过退偏器之后仍包含一部分的偏振光。浙江大学罗敬等人以激光为光源，在测试退偏器的退偏效果时，发现测试结果也类似图9中余弦分布的情况[28]。这说明即使在对准偏失角为 0°的情况下，增益比定标结果仍会受到该部分偏振光的影响。

需要注意的是，退偏器法测量的数据中只有5组数据的对准偏失角在−45°～ +45°内，所以该种方法在图7中只标有5个点。退偏器法在θh=0°时，相对误差为5.6%。这说明即使在对准偏失角为0°的情况下，增益比定标结果仍会受到该部分偏振光的影响。

4.4 讨论

通过对实验结果进行分析，可得知±45°法、∆45°法与旋转拟合法定标结果最为准确，这和前文的理论分析一致。但是±45°法在对准偏失角较大的情况下误差较大。旋转拟合法定标耗时较长，操作繁琐，只适用于相对稳定的大气环境下。相比之下，∆45°法操作更为简便，定标结果不受对准偏失角的影响，而且也无需进行初始0°角的搜寻，优势明显。但是，∆45°法也无法排除大气状态变化的影响，相比之下，只有退偏器法同时具有操作简便，可排除大气状态变化影响的能力，而且也不存在多次旋转半波片会增加角度积累误差的问题，但目前商用退偏器仍无法产生完全的退偏光，这会引入新的误差，且难以评估。综上所述，建议偏振激光雷达研究人员在一般情况下采用∆45°法定标，在有高精度退偏器的情况下采用退偏器法定标。

5 结 论

增益比的定标准确性对偏振激光雷达探测精度影响很大。本文系首次在原理与实验上对比了现存多种增益比定标方法，并给相关研究人员提出了增益比定标方法选择的指导意见。

就可操作性而言，退偏器法只需在系统中插入退偏器即可完成定标，可排除大气状态改变造成的影响，而其余需要旋转半波片的4种方法至少需要完成两次旋转，操作相对复杂，而且无法排除大气状态改变造成的影响。就定标准确性而言，实验主要对比了+45°法、±45°法、∆45°法、旋转拟合法与退偏器法等5种方法（由于洁净大气分子法定标误差较大，本文未作实验对比）在不同对准偏失角下对增益比定标的影响。实验结果表明，±45°法、∆45°法与旋转拟合法的定标准确度相对较高，但±45°法与旋转拟合法操作较为复杂。±45°法在对准偏失角较大的情况下误差较大。∆45°法增益比定标结果不受对准偏失角的影响，而且也无需进行初始0°角的搜寻。+45°法相对于前3种方法在没有对准偏失角的情况下误差更大。退偏器法受到非理想退偏器的影响较大，如果存在理想退偏器，那么这种方法将是一种理想的增益比定标方法。通过对不同增益比定标方法理论与实验的对比，本文给出了增益比定标方法的最佳选择，即建议在一般情况下采用∆45°法定标，有高精度退偏器的情况下采用退偏器法定标。