利用反射式圆光栅的振镜转角测量

刘永坤，丁红昌 ，向 阳 ，吕思航

（1. 长春理工大学 光电工程学院，吉林 长春 130022；2. 长春理工大学 机电工程学院，吉林 长春 130022）

1 引 言

在机械制造、仪器仪表以及各类电子产品制造中，角度测量精度一直是重要的指标之一，其精度的高低直接影响着产品质量的好坏。为了提高测量精度，各类测角技术层出不穷，据不完全统计，角度测量方法按测量原理大致可以分为16类[1-3]。在这些测角方法中，光学测角法越来越受到关注，而相较于电感、电容微位移测量、激光位移测量等系统，基于光栅的测量系统具有精度高、分辨力高、体积小、抗干扰性强、成本低、工作环境要求低、使用方便等优点，具有巨大的应用潜力，得到了广泛应用[4-10]。

随着光学测角技术的不断发展，针对扫描振镜的角度测量设备也在更新换代，为了得到响应快、精度高、误差小、结构小巧的角度检测器，国内外开展了许多研究。目前国外研究较好的公司也是生产高质量扫描振镜的公司，主要有SCANLAB公司、GSI公司、CTI公司、RAYLASE公司等，他们利用高精度电位器、角度编码器等作为扫描振镜的角度位置闭环，以此实现整个闭环系统的设计，其产品精度一般在2 μrad以内。同时，国外许多学者在此方面也做了大量研究，如宫岛广史将集成传感线圈构成的扫描控制器作为角度控制闭环，研制了一种电磁光学扫描仪，其稳定性误差小于0.1%。相比于国外，国内厂商起步晚，技术也不如国外成熟[11-14]。为促进我国在这方面的研究，国内相关学者围绕振镜控制系统相继开展了许多研究，如华中科技大学的叶乔设计了扫描振镜中电机控制系统的位置反馈环节与电流反馈环节，根据系统整体设计了PID控制校正装置[15]；中国科学院西安光学精密机械研究所井峰采用以PSD为主控制器的数字式控制系统，以位置－电流－速度三闭环控制为基础，以算法为控制策略，实现了振镜的高速与高精度控制，同时也提出了改进算法[16]。

为了使扫描振镜有更好的角度闭环，优化扫描振镜的闭环电路，提高振镜转角测量精度。本文基于衍射与干涉理论，推导了振镜转角与干涉条纹强度变化的关系，在Matlab中进行了仿真，给出了整个系统的最优解，并通过具体实验进行了实际验证。

2 测量原理

设计的振镜转角测量装置光路如图1所示，其主要可以分为5部分：光源准直部分、反射镜部分、衍射部分、干涉部分、信号处理部分，其各部分的组成主要包括激光光源、准直透镜、反射镜、干涉透镜、狭缝、折转棱镜、光电转换器、信号处理电路、上位机。

图 1 振镜转角测量光路Fig. 1 Optical path of galvanometer’s rotational angle measurement

从激光光源发出的光，先经过准直光路进行准直，随后经过与振镜同轴设计的反射镜反射进入反射式圆光栅，此反射式圆光栅的圆心位于反射镜的中心轴线上，在反射式圆光栅上产生的±1级衍射光，再次经过反射镜反射后，进入汇聚透镜，之后通过狭缝进行干涉，利用能量较大的±1级衍射光进行干涉。为了避免结构过长，利用折转棱镜折转±1级衍射光，以使结构紧凑并把干涉条纹呈于光电转换器上。振镜转动时，带动反射镜转动，使得入射到反射式圆光栅的入射角改变，相应产生的±1级衍射光也发生转动，使得干涉部分的两束光线的相位差发生改变，从而引起干涉条纹光强的改变，进而把角度转动量转化为干涉条纹光强的变化。通过光电转换器把干涉条纹光强的变化转化为电信号，通过后续的信号处理电路以及上位机，直接计算得出角度量。

3 模型建立

光源发出的光线经过准直透镜后，以一定入射角入射到反射镜上，其反射角与入射角相等，遵循光的反射定律。当振镜工作时，与振镜同轴设计的反射镜同步转动，反射镜转角即振镜转角，其法线也在不断转动，使得入射角不断改变，而此时的反射光线也随之不断改变[17]。反射角的改变直接影响着后续进入反射圆光栅的夹角。为了得到反射镜转角与反射光线改变角φ的关系，设置初始入射光线与反射镜转轴共面，如图2（彩图见期刊电子版）所示。

图 2 初始入射光路示意图Fig. 2 Schematic diagram of the initial incident light path

平面A为反射镜平面，绕着中心轴旋转，平面B为反射镜法线所在平面，EO为经准直光路准直后到达反射镜的入射光线，初始入射角为γ，OM、ON分别为反射镜摆动至最大角度时所对应的出射光线，OC、OD分别为相应的反射镜法线，则∠COT=∠DOT=α，α为反射镜向两侧的转动角度，∠EOC和∠EOD分别为反射镜摆动至最大角度时的入射角，即β1和β2，且β1=β2=β。

图3是把图2中三棱锥放大旋转，图中阴影面CODT为法线所在平面，由反射镜转动知∠COT=∠DOT=α，∠EOT为初始入射角γ，做垂线ET⊥OT，平面MOE和EON是入射角分别为β1和β2时的入射平面，OC和OD为两入射面的法线。由几何关系知OC⊥ME，OD⊥EN，由ET垂直平面CODT，知ET⊥OC。由OC⊥ME，OC⊥ET，ME∩ET=E，则OC垂直平面CET，进而有OC⊥CT，所以OC=OT·cosα。

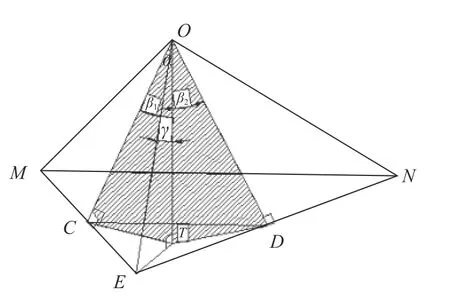
图 3 改进的初始入射光路图Fig. 3 Diagram of improved initial incident light path

由几何对称关系可知：OM=OE=ON=b，β1=β2=β，MC=CE=ED=DN=bsinβ，∠EOT=∠DOT=α，∠MON=φ。在ΔOTE中，ET⊥OT，则有OT=OEcosγ，即OT=bcosγ；在ΔOCE中，OC⊥ME，则 有OC=OEcosβ1，即OC=bcosβ。由 以 上可知：

式(1)即为反射镜入射角与初始入射角和反射镜转角的关系，即在反射镜初始入射角确定时，反射镜入射角随反射镜转角变化而改变。

在ΔOCD中，由余弦定理知：CD2=OC2+OD2−2OC·ODcos ∠COD，又由OC=OD=OEcosβ，∠COD=2α得：

在ΔMEN中，由于MC=CE=ED=DN，则C、D分别为ME、NE的中点，所以有2CD=MN，进而有MN2=4CD2。

在ΔMON中，由MN2=4CD2，由余弦定理可得：

将式(1)代入上式有：

由式(2)可知反射镜转动角度α与出射光线角度变化量之间的关系。

如图4所示，光线从反射镜反射进入反射式圆光栅产生衍射，产生的衍射光再经反射镜反射进入干涉部分。

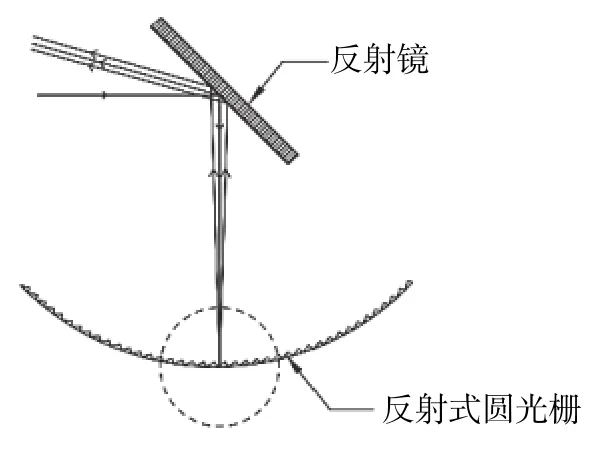
图 4 反射式圆光栅光路图Fig. 4 Optical path diagram of reflective circular grating

反射式圆光栅成周期性变化，并且每个栅面到圆心的距离都相等，其在不同栅面同一相对位置时产生的衍射效果也都相同，因此只需分析其在一个栅面上的衍射效果即可。图5为图4中虚线部分放大的单个栅距上的光路图。

图 5 单个栅面上的光路图Fig. 5 Optical path diagram on a single grating surface

如图5所示，经反射镜反射的光进入反射式圆光栅，入射光线和衍射光线均在光栅主截面内。设入射波长为λ，入射角和衍射角分别为i1和θ1，光栅常数为d，衍射级次为m，当入射光线改变Δφ时，人射角和衍射角变为i2和θ2，入射光线改变前后，入射角与衍射角的改变量分别为Δi和Δθ。根据文献[18]知光栅方程d(sini±sinθ)=mλ，由于入射光线与衍射光线不同侧，则光栅方程为d(sini−sinθ)=mλ。由此知：

由于入射角i1与 衍射角 θ1的改变量分别为Δi和Δθ，入射角和衍射角变为i2和θ2，则有

将式(4)代入式(3)，由于Δi和Δθ为小角度量，满足小角度近似条件，整理可得：

进入反射式圆光栅的入射角改变量即为从反射镜出射光线角度的改变量φ。由式(5)可知，当初始入射角与初始衍射角确定以后，衍射角改变量与进入反射式圆光栅的入射角改变量成线性关系。

从反射式圆光栅产生的能量相对较大的±1级衍射光，再次经过反射镜反射进入汇聚透镜，经过狭缝进行干涉。该装置用于振镜转角测量，本文利用折转棱镜进行光路转折以使该装置小巧、紧凑。同时，为了避免零级衍射光的干扰，狭缝间距按一定距离进行设计。具体光路如图6所示。

图 6 干涉光路图Fig. 6 Interference optical path diagram

已知相邻零值之间的角间距为[19]：

式中Δω为主极大的半角宽度，N为刻槽数，λ为入射波长，d为光栅常数，θ为衍射角度。而又由于sinθ=0对应零级衍射，此时cosθ=1，故零级衍射角宽度可由几何关系获得：

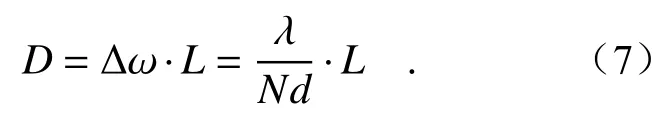
分析单个槽面的零级衍射时N=1，代入式(7)可求得狭缝间距D，该间距下可拦截零级衍射光，避免零级衍射光干扰，提高测量的准确性。

设±1级衍射光两相干平面波的振动U1(x,y)和U−1(x,y)分别为：

式中A1和A−1分别为±1级衍射光的振幅；ω1和ω−1分别为±1级衍射光的角频率，φ1和φ−1分别为其初始相位。

利用反射式圆光栅产生±1级衍射光，经过反射镜汇聚后进行干涉。设±1级衍射光叠加时所产生的干涉条纹光强分布I(x,y)为：

由此可得：

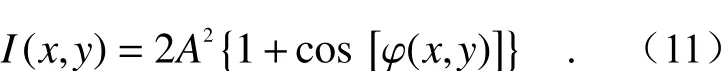
由式(11)可知，干涉条纹强度不随时间变化，只呈稳定的空间分布。随着±1级衍射光初始相位差的改变，干涉条纹的强度分布表现为有偏置的正弦分布。

由式(2)知，当给定入射角γ时，反射镜转动角度α与出射光线角度变化量之间满足以下关系：

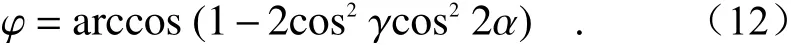
由于从反射镜反射的出射光线即为反射圆光栅的入射光线，故Δi=φ。由式(5)所表示的衍射角改变量与进入反射式圆光栅的入射角改变量间的关系可知，当初始入射角确定为零时，±1级初始衍射角分别为：

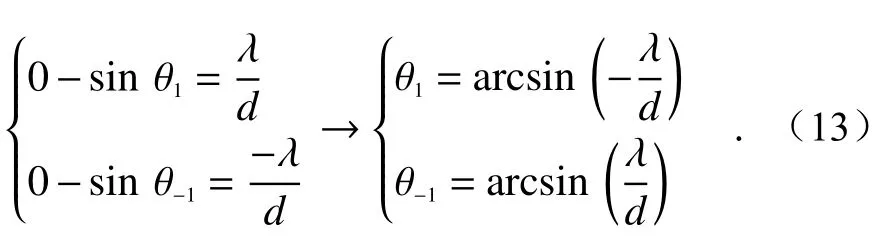
由于±1级衍射光的初始角度相反，故当反射镜转动时，±1级衍射光的初始相位分别为：

而θ1=−θ−1， 即∆ θ1=∆θ−1，进而有：

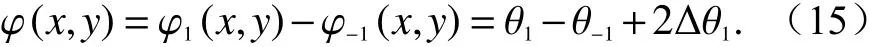
将式(5)、式(12)与式(15)代入式(11)可得反射镜转角α与干涉光强的关系式：

式中A、θ1、θ−1以及γ均为定值，故可得出光强随反射镜转角α的关系。

4 模型仿真

为了进一步确定反射镜转动角度与干涉光强的关系，结合实例对上述公式做进一步分析。首先是光源的确定，相比于其他光源，激光的亮度比较高，在时间和空间上光能比较集中，具有较好的相干性[20]；同时激光的单色性与方向性也比较好。实验仿真选用650 nm的激光作为检测光源。当反射式圆光栅栅距确定时，入射到反射圆光栅的初始角度θ1与θ−1就随之确定了。实验仿真选用光栅常数为18 μm的反射式圆光栅，刻线为1024条，则θ1与θ−1分别为2.0695°与−2.0695°。A为条纹光强的直流分量，当光源确定时，A就随之确定且为一常量，这里为方便计算可取A=1。此时，式(16)可转化为：

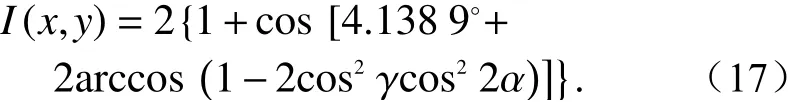
由式(17)可看出，干涉光强的变化与光源的初始入射角γ以及反射镜转动角α有关。

由于反射式圆光栅栅距呈周期性排列，故只需分析光线在单个栅面上移动时的干涉光强的变化即可。利用Matlab软件对式(17)进行计算，可以得到图7所示关系曲线，由此可知当反射镜转动时，干涉条纹强度也呈周期性变化[21]，通过后续的信号处理电路以及上位机进行计数处理，得出所测的角度量。

图 7 干涉条纹光强图Fig. 7 Light intensity diagram of interference fringes

为了进一步寻找最佳初始光线入射角，即激光器的初始入射角，通过分析一个周期内不同初始入射角γ下的干涉条纹光强，利用Matlab软件得出不同入射角下的干涉条纹光强图，如图8所示。

图 8 初始入射角γ分别为（a）10°、（b）30°、（c）45°时的干涉条纹光强图Fig. 8 Interference fringe intensity diagrams at initial incident angles of (a) γ=10°, (b) γ=30°, (c) γ=45°.

从图8可以看出，入射角越小时，其干涉条纹光强越强，为了使结构紧凑，可使光源与汇聚透镜呈上下分布。但光源入射角不可能为零，光源大小、反射式圆光栅的参数要求，以及其结构限制使得光源入射角最小为10°，故为了得到最好的干涉光强，取光源入射角γ=10°。

5 验证实验

实验所用装置如图9所示。其中，圆弧型反射式光栅的光栅尺寸半径为15 mm，圆弧角度为70°且圆心处于反射镜转动中心的轴线上，光栅常数为18 μm，刻线密度为55 line/mm，总刻线数为1024条。激光光源波长λ为650 nm。准直透镜口径为3 mm。汇聚透镜口径为4 mm。狭缝间距为0.5 mm，两缝间距为0.542 mm。反射镜尺寸为6 mm×6 mm，与振镜同轴设计。折转棱镜为等腰梯形。

图 9 实验装置图Fig. 9 Experimental setup

本次实验电路为常规的信号处理电路，对反射式圆光栅单个周期所对应的转角0.0012 rad进行8位细分，使其分辨率达到1″，之后对测量角度进行验证。选用美国的Aerotech一维转台的测量结果作为实际转动角，而该装置测量的反射镜转动角作为测量角。对不同反射镜角度进行20次测量，结果见表1。

表1 角度测量结果Tab. 1 Angle measurement results (°)

20次实验测量拟合出测量角和实际转动角的曲线关系：

式中y为测量角度，x为实际转动角度。由图10可知测量角和实际转动角拟合结果呈线性关系。受仪器误差、环境因素、操作等[22]的影响，该检测设备的线性度只能无限接近1，相对测量误差为0.044%，测量精度为0.00269°，即10″以内。

对20次实际测量的误差值进行散点分布，如图11所示。可见，除个别跳跃点以外，测量误差成规律性分布。同时可以看出，振镜转角越大时，相应的误差值也越大。误差较大的原因总体可分为两点：一是设备本身加工装调以及其所处的外界环境温度、设备振动等带来的误差；另一点是振镜转角与反射镜出射光线的非线性关系引起的误差。通过上述实验可知，在振镜转角±10°时，线性度达到99.956%，无限接近于1。

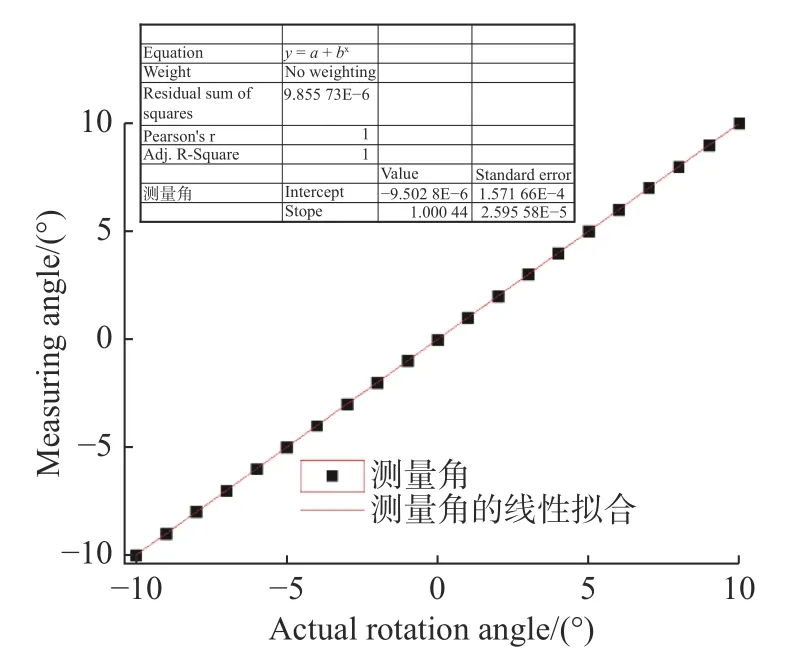
图 10 振镜转角测量结果Fig. 10 Measurement results of galvanometer’s rotational angle

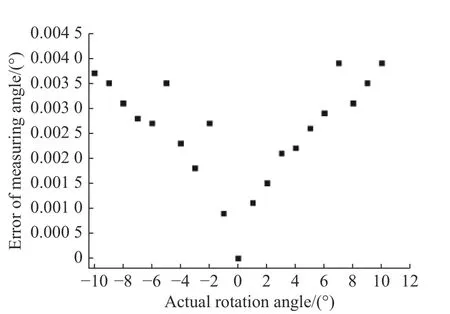
图 11 误差散点图Fig. 11 Error scatter plot

6 结 论

根据现代化振镜转角测量系统的小巧化、高精度的要求，提出了利用反射式圆光栅测量振镜转角的方法，并介绍了反射式圆光栅振镜转角测量系统的组成与测量原理，搭建相应的数学模型，给出了仿真结果，并通过具体实验进行验证，最后给出了测量振镜的角度范围以及测量精度。实验结果证明：利用反射式圆光栅产生的±1级衍射光干涉方法，实现了振镜±10°转角的高精度测量；测量精度为10″。基本满足振镜角度测量的高精度、小巧化的要求。