工业机器人时间-冲击最优轨迹规划

胡 杰，李先祥* ，欧道江，肖红军

（1.佛山科学技术学院机电工程与自动化学院，广东佛山 528225；2.佛山智能装备技术研究院，广东 佛山 528225）

工业机器人最优轨迹规划求最优解的研究主要分为考虑运动学或者动力学约束、运用遗传等智能优化算法及转化为其他数学模型等3 类通用性解法［1］，目前国内外专家学者均做出了一些研究［2-5］。本文对传统遗传算法进行改进，在保证机器人运动平稳的条件下，优化了机械臂动作时间和运动过程中的冲击量，使机器人能够稳定平顺运行。

1 HSR605 建模及轨迹规划

1.1 运动学建模与动力学建模

以6 自由度的HSR-605 机器人为研究对象，采用标准DH 法建立机器人的连杆坐标系，通过机器人运动学参数和动力学参数建立其数学模型，机器人参数如表1 所示。

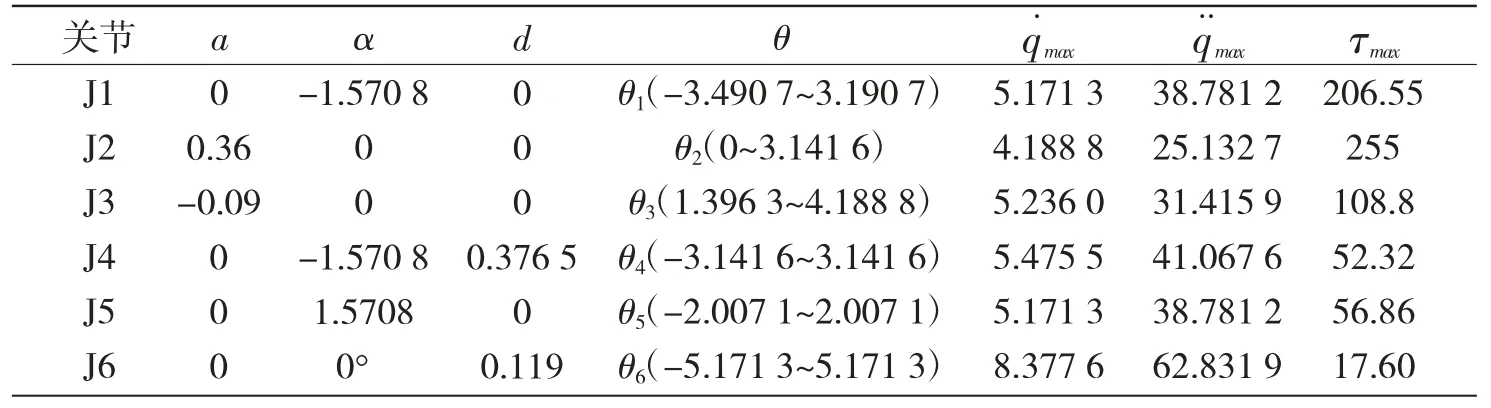
表1 HSR-JR605 机器人运动学与动力学参数

对于6 自由度机器人，其正向运动学方程为

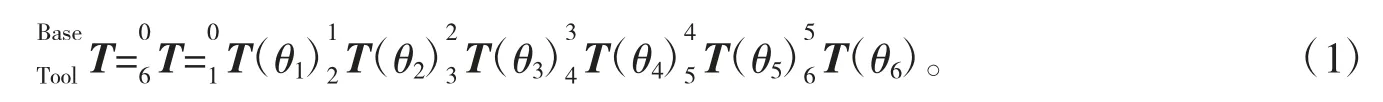
采用拉格朗日法进行数学推导，建立基于HSR-605 机器人的动力学方程为

其中，τ 表示关节力矩矩阵，M（q）表示惯量矩阵，C（q）表示耦合惯量矩阵，G（q）表示重力矩阵。

1.2 五次多项式轨迹规划

为保证离散轨迹上关键节点处速度和加速度的连续平滑，采用五次多项式对关节空间下轨迹的关键路径点之间的位置、速度、加速度和加加速度曲线拟合，五次多项式表达式如下

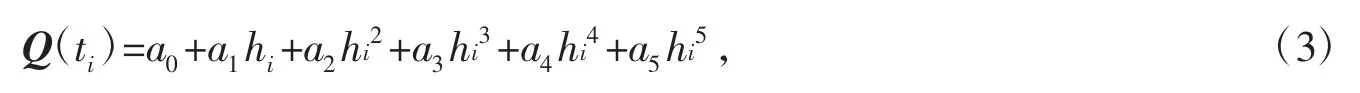
其中，a0～a5为五次多项式系数；hi=ti+1-ti，而ti和ti+1分别为某段路径起点和终点对应的时间序列。

每一个五次多项式表达式都有6 个未知系数待求解，因此需要6 个约束条件才可以唯一确定各项系数［7］。将轨迹曲线代入位置、速度和加速度的约束条件，整理成矩阵形式为

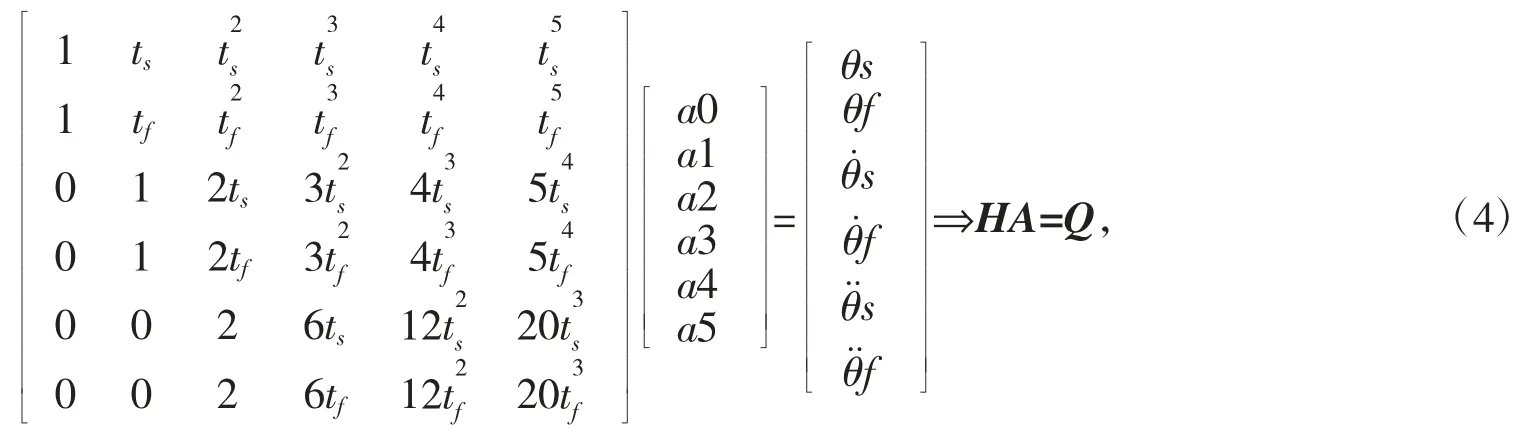
其中，ts、tf、θs、θf、分别为起点和终点的时间、位置、速度、加速度，A 为各段路径的五次多项式系数矩阵，H 为时间矩阵，Q 为各个路径关键点位置矩阵。

2 优化问题数学描述

对关节空间给定各路径点的速度与加速度，相邻路径点之间用五次多项式进行插补，则关节轨迹由运动时间序列｛t1，t2，t3，…，tm-1｝可以唯一确定，故机器人的时间性能指标和冲击性能指标可表示为

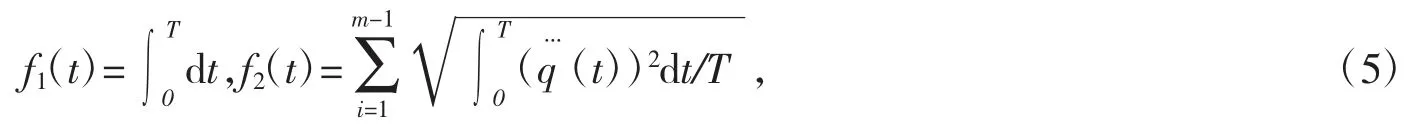
运用权重法将多目标约束问题转化为单目标约束问题［3］，建立混合目标函数为

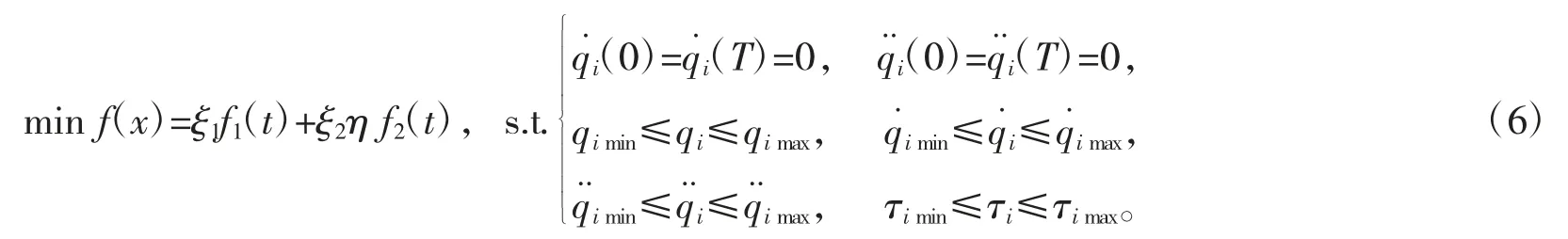
3 基于改进遗传算法的轨迹优化

3.1 生成适应度函数

基于遗传算法的轨迹优化是通过将轨迹优化问题解的搜索空间映射到遗传算法求解空间。首先将轨迹运行时间进行编码并初始化，然后根据目标函数设置的适应度函数计算种群个体的适应度，从而选择适应度高的个体反复进行交叉和变异产生新的种群，最终得到满足约束条件的近似最优解。

采用罚函数法来处理不等式约束，对不满足约束条件的个体进行惩罚，其表达式为

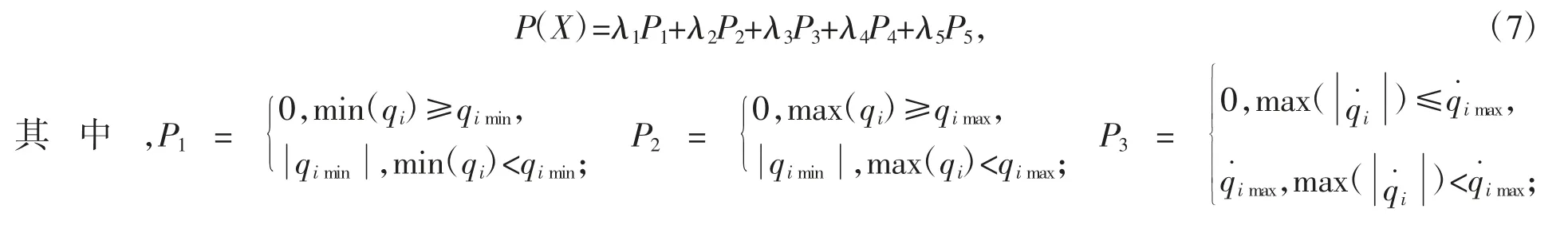
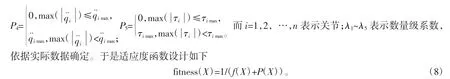
3.2 改进遗传算法

（1）交叉算子改进策略。首先本文采用锦标赛方法，从所有个体中随机抽取一半进行锦标赛，若随机数r≤0.5 则选出适应度最佳的两个个体，否则在锦标赛集合内随机选出两个个体。然后引入海明距离的概念，对于进行交叉操作的两个个体计算海明距离，根据海明距离判断染色体上基因位是否相同，相同则在染色体内进行基因重组，否则进行染色体数值交叉。设X1和X2表示锦标赛法选择的两个染色体，X'表示交叉后的种群，α 取｛0，1｝间的随机数，cs 表示染色体进行基因重组，则交叉公式为

（2）变异算子改进策略。计算当前染色体基因与当代最优染色体对应基因位的欧氏距离，根据欧氏距离进行变异大小判断，欧式距离越小表明该染色体越接近最优解，则进行小变异。设X 表示当前种群，Xu和Xl分别表示种群上限值和下限值，X'表示变异后的种群，r=rand（0，1），B（k）和T（k）表示当代种群最优染色体和当前选择的染色体对应的基因，g 表示当前代数，Gmax表示最大迭代次数。染色体基因的欧式距离为，则变异公式为

（3）遗传操作概率改进策略。为了保护优良染色体，根据每一代种群和当前染色体自适应生成交叉和变异概率。首先计算交叉和变异后种群适应度的平均值，即；其次计算交叉和变异后种群适应度的标准差，即；最后根据上一代的适应度标准差自适应调整交叉和变概率，即其中pc1=；fc和fm分别是交叉个体和变异个体的适应度值；pc0和pm0为给定初始交叉概率和变异概率。

基于改进遗传算法的五次多项式最优时间-冲击轨迹规划方案的步骤为：1）采用实数编码方式对染色体编码，以时间间隔h 为自变量，即h=［h1，h2，h3，…hm-1］。2）以均匀方式产生初始种群有利于全局搜索。3）采用五次多项式进行轨迹规划。4）根据式（8）计算种群适应度。5）根据系数ps选择出个精英个体，采用锦标赛法从精英个体中随机抽取子代个体。6）采用锦标赛法选出两个个体，并根据海明距离判断交叉类型而进行交叉操作。7）根据当前染色体基因与最优染色体对应基因位的欧氏距离确定染色体变异大小。8）精英父代种群替换子代种群中适应度较差的个体更新种群。9）达到最大迭代次数则停止，否则跳转到步骤3）继续迭代。10）停止迭代，根据最优时间间隔序列进行最优轨迹规划。

3.3 轨迹优化仿真

为验证所提出的改进遗传算法的性能，采用本文改进策略对文献［5］的时间最优轨迹规划问题进行求解，与文献［4］和［5］对比，结果如表2 所示。由表2 可知，本文结果具有更强的寻优能力。

表2 算法测试结果对比s

为探讨适应度函数中ζ1、ζ2权重系数的取值对时间和冲击两种指标优化结果的影响，采用如表3所示的7 段路径曲线作为验证算法的给定输入路径，机器人的各约束条件如表1 所示。

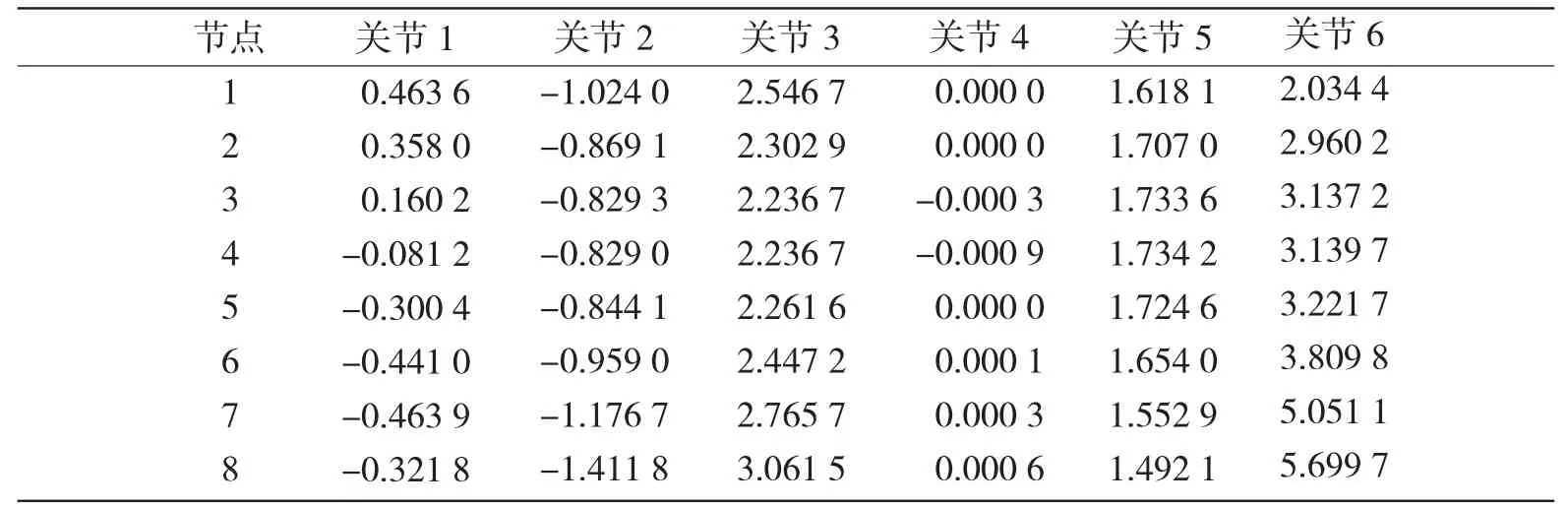
表3 关键点关节位置序列

在时间-冲击最优轨迹规划问题中，遗传算法参数设置为：Dim=7，Pop=60，Gmax=200，ps=0.2，pc0=pm0=0.5，λ1=0.1，λ2=0.1，λ3=0.1，λ4=0.01，λ5=0.001，η=0.01，再设定不同的权重系数值ζ1（保证ζ1+ζ2=1）。最后进行多次仿真实验得到时间-冲击优化的结果如表4 所示。

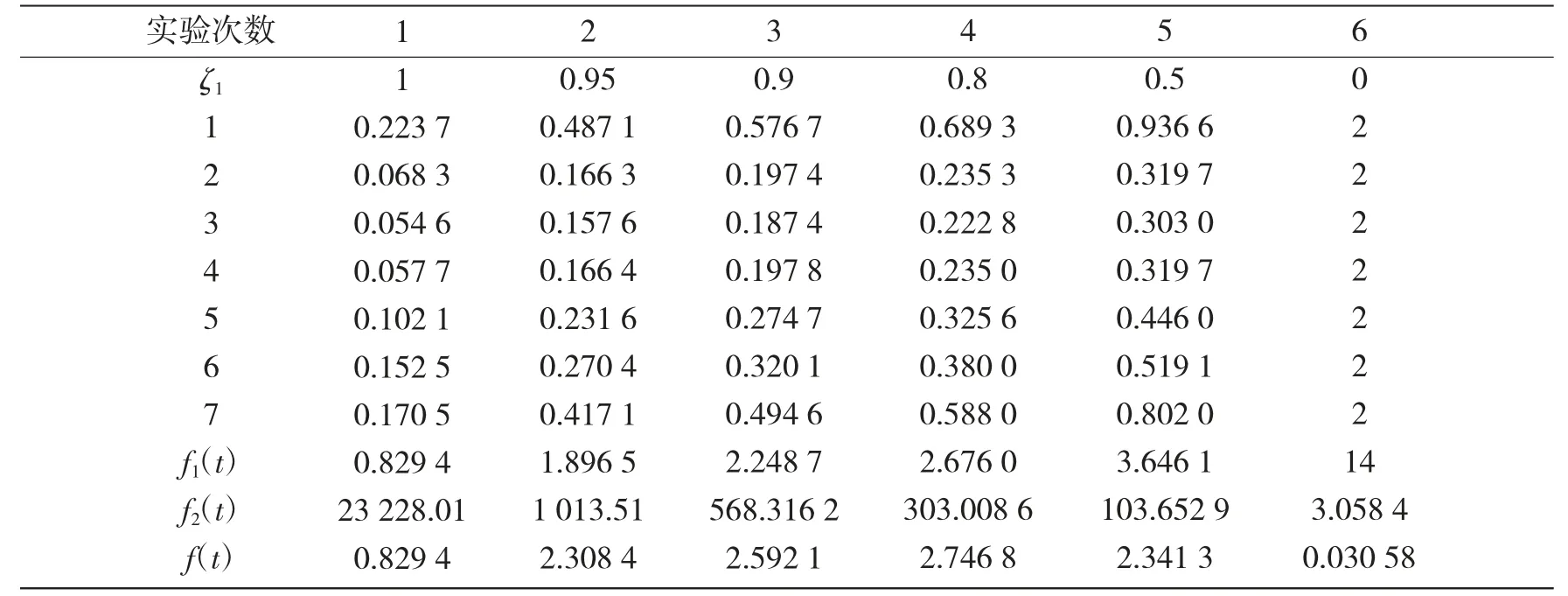
表4 最优时间序列

由表4 可知，随着ζ1值减小时间目标函数权重减小，f1（t）变大，f2（t）变小，且冲击指标f2（t）的下降的幅度较时间指标f1（t）的增加幅度大，说明权重变化对冲击指标f2（t）的影响较大。综合考虑后选取加权目标函数较优的第4 组数据（ζ1=0.8，ζ2=0.2）进行5 次多项式曲线拟合，仿真结果如图1～5 所示。

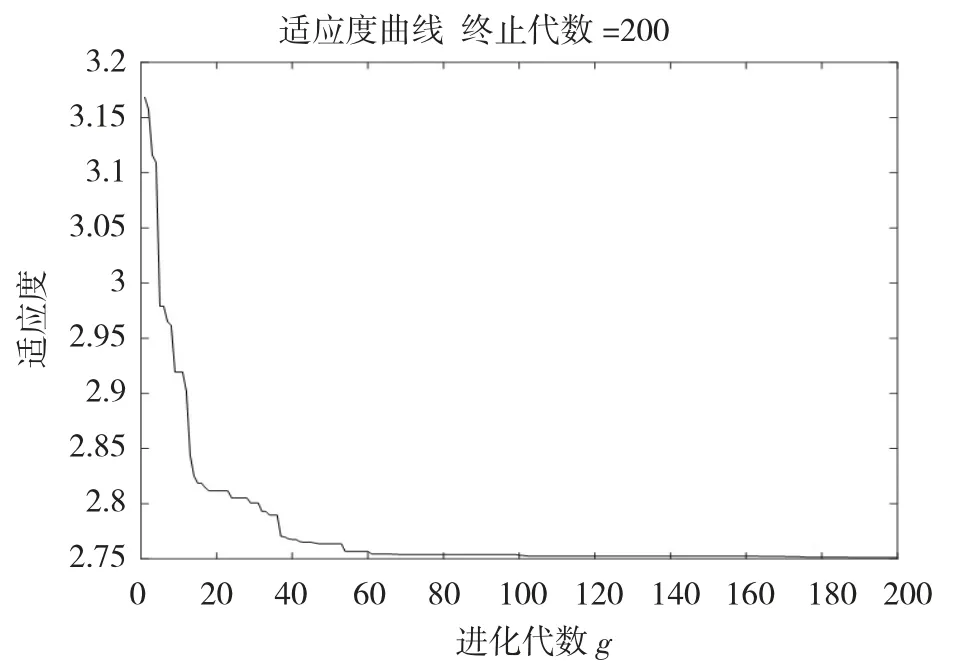
图1 算法迭代收敛曲线

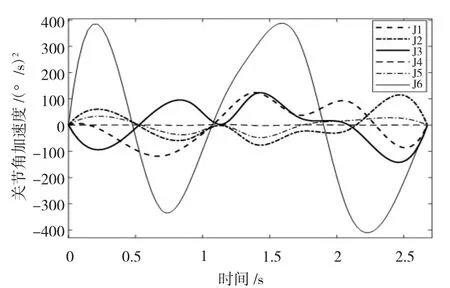
图4 关节角加速度曲线

由图1 可知，算法迭代60 次后适应度幅度变化逐渐趋于稳定，算法收敛速度较快。由图2 可知，优化后各关节拟合的轨迹均能通过给定的关键路径点。由图3～5 可知，优化后的关节角位置、角速度、角加速度、角加加速度和关节力矩曲线均连续和平滑，起点和终点处速度、加速度均为零。

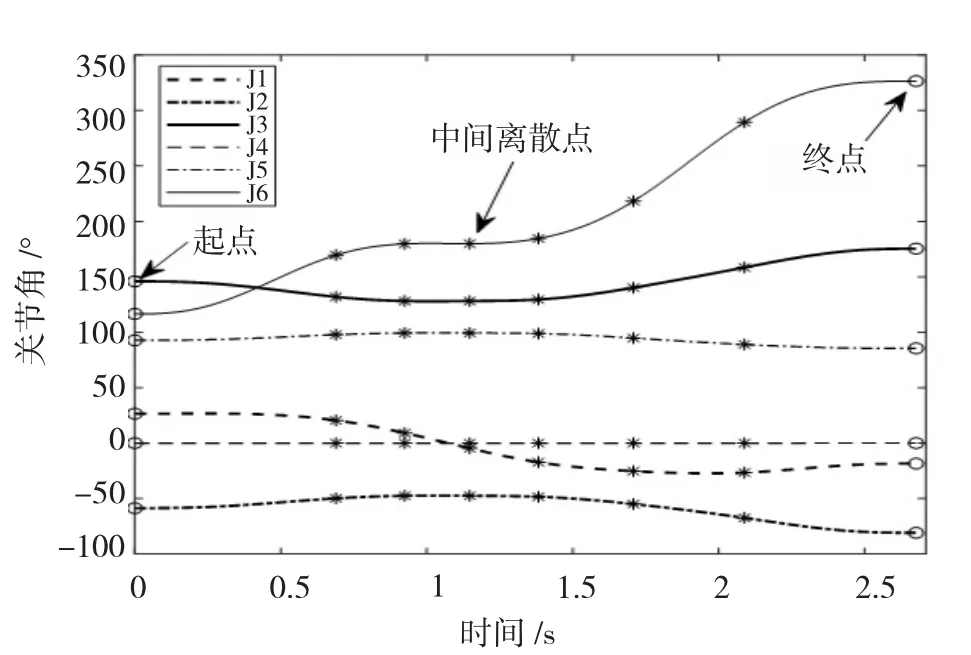
图2 关节角位置曲线

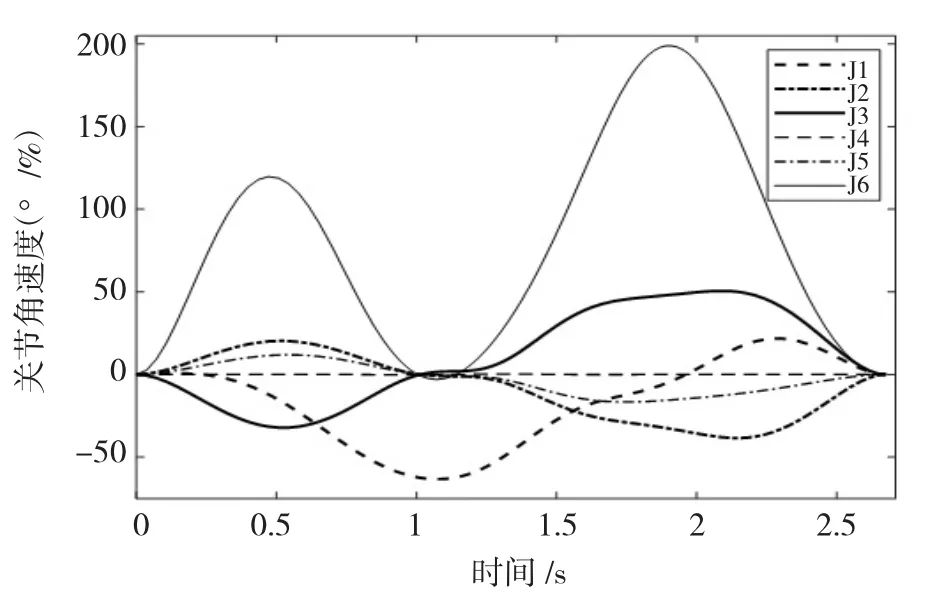
图3 关节角速度曲线

综上所述可知，本文基于改进遗传算法的时间-冲击最优轨迹规划方法能够得到运行时间较短、平稳性较好的轨迹。

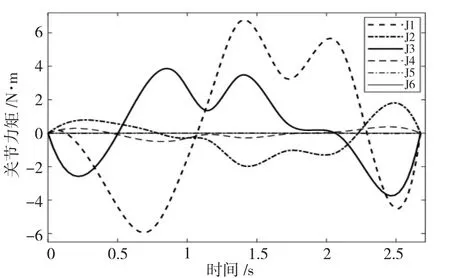
图5 关节力矩曲线

4 小结

通过与文献［4］和［5］结果对比可知，本文改进遗传算法性能更优，能够规划出较好的混合最优轨迹，从而实现六自由度机器人较高的运行效率和平稳性的研究目标。