π型叠合梁颤振试验及数值研究
汪志雄 张志田 吴长青 郄凯

摘要: 基于某π型叠合梁断面进行了颤振试验及颤振导数试验,试验结果表明断面的颤振形式是极限环振动(LCO)而非发散振动;分析了断面的后颤振极限环及频率演变特性;采用了基于阶跃函数的后颤振自激力模型并通过试验验证了其在计算颤振临界风速及后颤振幅值方面的精度及可靠性,进一步分析了数值计算和试验两者之间产生误差的成因;对比分析了几何非线性在后颤振数值计算中的作用;采用伪稳态自激力分离法解决平均风荷载重复计入的问题;研究了在+3°攻角下不同结构阻尼比对π型断面颤振临界风速及后颤振幅值演变的影响,研究表明π型断面的颤振和后颤振对结构阻尼具有较大的依赖性。数值计算结果表明,采用阶跃函数自激力模型成功地实现了平均风效应及几何非线性的时域分析,为分析大跨径桥梁的非线性后颤振性能提供理论依据及求解策略。
关键词: 风洞试验; 后颤振; 非线性; 阶跃函数; 极限环
中图分类号: TU311.3; U441+.2 文献标志码: A 文章编号: 1004-4523(2021)02-0301-10
DOI:10.16385/j.cnki.issn.1004-4523.2021.02.010
引 言
由于美国原Tacoma桥的风毁事件,桥梁的颤振失稳被认为是毁灭性的,即当风速达到临界点之后结构出现动力失稳,其振幅不斷增大直至结构破坏。多年来,桥梁的颤振稳定性采用一个临界风速来描述[1?5],在设计上要求颤振临界风速不低于颤振检验风速。这一方法最大的缺点是忽略了颤振临界点断面气动性能的优劣,不能体现桥梁的后颤振抗风的强健性。原Tacoma大桥与金门大桥的历史表明[6],不同的后颤振性能对结构颤振后的振幅甚至结构的命运起着决定性的作用。航空航天领域研究也表明,由于结构非线性、气弹非线性及二者组合的作用,细长薄机翼的颤振形式是一种振幅较小的极限环振动(LCO)[7]。因此,深入研究桥梁后颤振性能是必要的。
研究后颤振特性可能涉及三大类方法。第一类是使用风洞试验。Amandolese X等[8]通过风洞试验研究了双自由度平板的后颤振幅值及极限环特性;Zhang M等[9]和郑史雄等[10]也通过风洞试验对桥梁断面的后颤振进行了研究。这一类方法具有如下两个特点:(1)在接近颤振临界风速时,节段模型振动幅值较小,因而弹性悬挂系统的几何非线性特性可忽略,这样能准确得出桥梁节段的颤振临界风速;(2)当试验模型振幅较大时,弹性悬挂系统的非线性特性明显,但和实桥的非线性特性具有较大的差异,因此节段模型风洞试验的后颤振特性并不能代表实桥的后颤振特性,但能作为验证自激力理论模型可靠性和适用性的依据。第二类是直接采用计算流体动力学(CFD)和结构运动方程相结合的方法[11?14]。这类方法没有引入任何半经验或经验模型,其可靠性依赖于所选CFD模型及网格质量,且计算成本巨大。第三类方法是在试验的基础上,引入半经验的非线性模型来描述气弹效应。目前为止,比较著名的有Tran C T和Petot D 1981年提出的ONERA模型[15],已经广泛地应用于处理直升机机翼及风力机叶片的失速问题[16?17]; Leishman 和 Beddoes 提出了另一种半经验模型[18],该模型在解决动力失速问题上得到了广泛的应用[19?20]。Larsen 等也提出了专门描述风力机叶片的非线性气动力的半经验模型[21]。Diana G等提出了以瞬态风攻角及其一阶导数为变量的非线性气动力模型,该模型可以描述给定振幅下气动力的滞回效应[22]。
以上半经验模型均描述滞回环特性,不能反映随振幅演变的气动力非线性特性,后者是桥梁非线性后颤振关注的关键。这方面有不少学者进行了尝试。王骑等采用平衡位置泰勒级数展开式建立了简谐波叠加的非线性气动力模型[23];Wu T和Kareem A提出了以Volterra 理论来体现非线性气动自激力效应[24];刘十一和葛耀君采用附加的非线性微分方程组与附加的气动力自由度的方法来模拟气动自激力随幅值演变的气动自激力的记忆效应以及非线性特性[25],该方法单独处理扭转的影响而不是采用动态风攻角的概念;朱乐东和高广中[26] 通过引入非线性气动导数来体现自激力随幅值演变的特性,该方法需要结合试验进行参数拟合,与试验结果吻合较好;Gao G等[27]采用三阶多项式描述气动力的非线性特性,该方法与试验结果取得了较好的一致性。Zhang M 等[28]通过引入和幅值及模态耦合相关的气动参数来描述气动自激力,该方法和CFD数值计算结果吻合较好,但适用性有待考证。吴长青和张志田[29]引入多阶段阶跃函数描述桥梁断面的非线性气弹效应,但缺乏试验验证。
理论上,节段模型和实桥的颤振临界风速基本上有一致性;节段模型的气动力非线性特性和实桥的也基本一致,但几何非线特性有显著差异,因而节段模型后颤振试验可用于验证气动自激力模型的可靠性。
本文通过风洞试验研究了π型叠合梁的气动性能,后颤振频率及幅值特性,采用了基于阶跃函数的后颤振自激力模型并通过试验验证了其在计算颤振临界风速及后颤振幅值方面的精度及可靠性,并分析了数值计算和试验两者之间产生误差的成因。为避免平均风荷载与气弹模型不兼容性所造成的气动力重叠问题,采用了阶跃函数气动力模型中分离出伪稳态响应的方法。通过数值计算研究了节段模型的颤振临界风速、后颤振幅值及极限环特性。
2 风洞试验
2.1 颤振试验
π型叠合梁节段模型颤振风洞试验在湖南大学HD?2风洞试验段进行。图1为悬挂于风洞中的模型。
节段模型由8根弹簧和两根横梁组成。两根轻质水平钢绞线约束了模型的横向运动。模型两端各装一块带倒角的椭圆端板以消除端部效应。
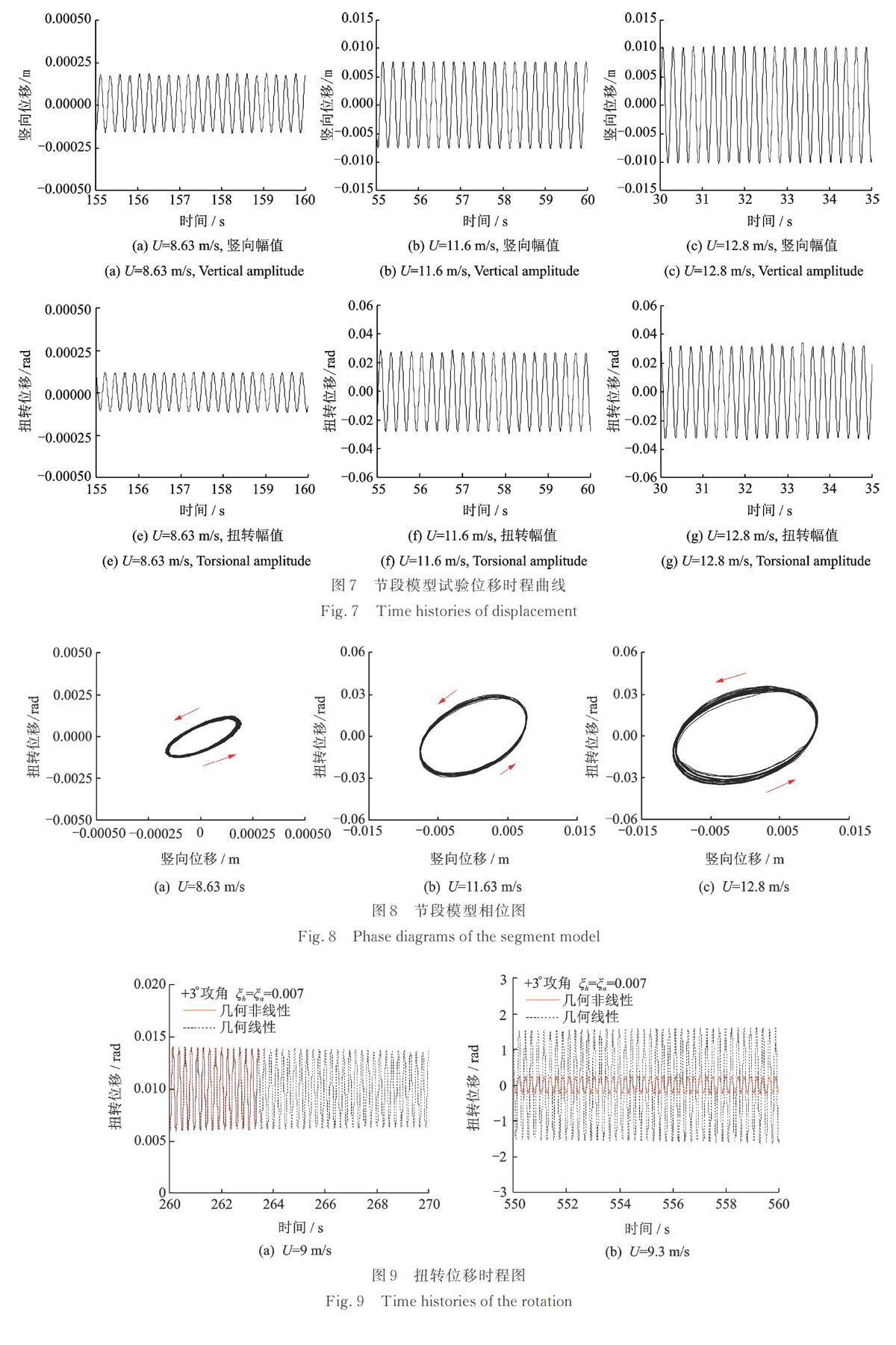
刚性节段模型总长度为1.54 m,其成桥状态横截面如图2所示。整个弹性悬挂系统等效质量为42.924 kg,等效质量矩为1.208 kg·m。模型的竖弯频率fh和扭转频率fα分别是4.160 Hz和4.321 Hz,竖弯阻尼比ξh和扭转阻尼比ξα为0.007。所有的测试都是在均匀来流下进行。+3°攻角下的颤振试验结果如图3所示,从图中可知,断面的颤振形式是LCO而非发散振动,且LCO随着风速的增大而增大。
2.2 颤振导数试验
利用三自由度强迫振动装置,在均匀流场中测试成桥阶段+3°,0°及-3°攻角下的颤振导数。通过竖向幅值为h/B=1/29和扭转振幅为2°的单自由度强迫振动得到了相应初始攻角下的颤振导数。结合图4中的成桥状态的三分力系数,+3°,0°及-3°攻角下的阶跃函数拟合值如表 1所示。
试验颤振导数和通过阶跃函数拟合的颤振导数示意图如图5所示。+3°,0°以及-3°攻角下颤振导数的拟合效果较好,尤其是对桥梁断面影响最大的气动导数A2*,这说明阶跃函数基本能够反映出断面的真实气动性能。
3 数值模拟
3.1 有限元模型
表2提供了有限元模型的动力参数。采用ANSYS有限元软件建模,其中刚性模型和横梁采用beam4单元模拟,弹簧支架采用link8单元模拟,质量和质量惯性矩采用mass21单元模拟。图 6为有限元模型设计图,和试验弹性悬挂系统一样,由8根弹簧、两根横梁及刚性模型组成。颤振时域计算时采用瑞利阻尼模型,阻尼矩阵C是由质量矩阵M和刚度矩阵K线性组合得到,表达式如下
C=αM+βK (26)
式中 α和β为瑞利阻尼系数。表2给出的α和β值对应竖弯和扭转阻尼比是0.007,与试验一致。
3.2 数值结果及数值模型验证
线性理论认为,当来流风速超过颤振临界风速Uc时,模型的振动响应就会发散。然而在实际风洞实验中刚性模型的振动响应会趋于一个稳定LCO。从图 7和8可以看出,在风速超过临界风速Uc之后,振动的幅值增加,模型达到了一个新的LCO,且随着风速的增加,后颤振的幅值也增加。当来流风速等于颤振临界风速Uc时,节段模型做振幅很小的等幅振动;当来流风速远大于颤振临界风速后,模型的振动并不能直接稳定下来,而是需要经历一段“拍”时间才能做等幅振动。从图 8可知,模型的竖向振动和扭转振动存在相位差,且随着风速的增加相位差也发生变化。
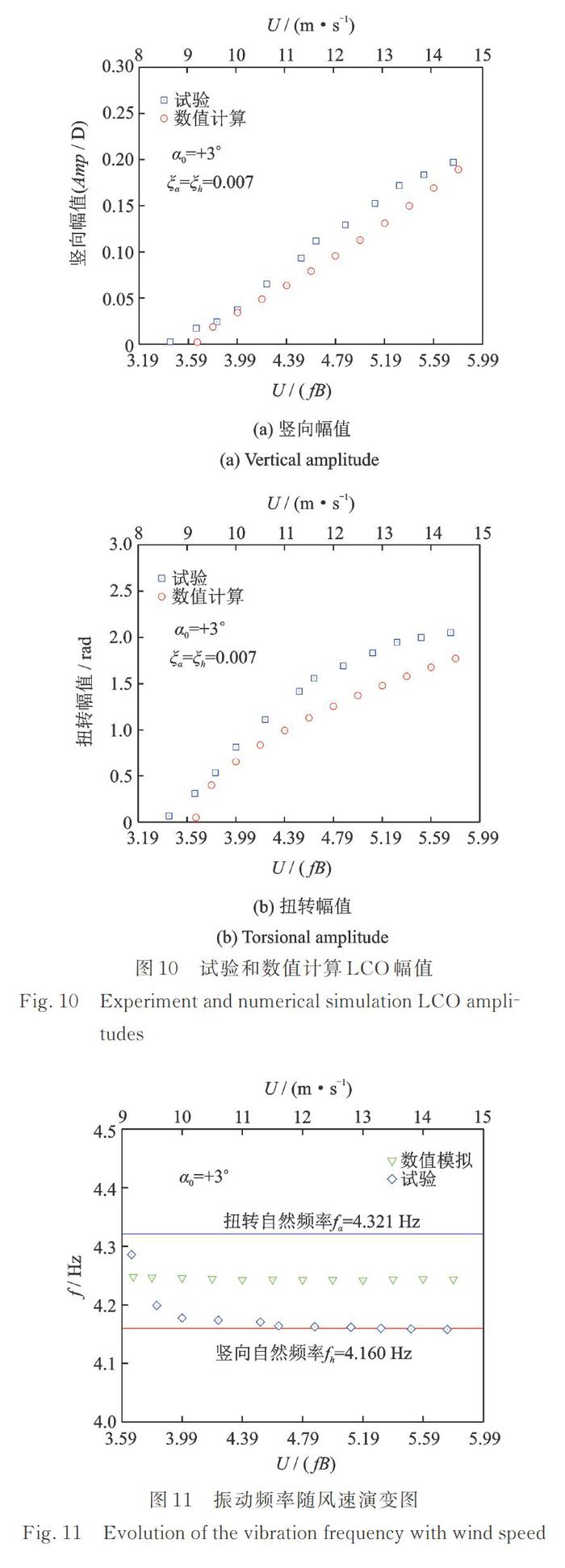
图 9给出了是否考虑几何非线性的对比,考虑几何非线性后,结构振动的形式由发散转为极限环振动。图 10给出了+3°攻角下节段模型试验和数值计算幅值随折算风速演变结果。颤振数值计算结果在颤振临界风速之后的小范围内和试验结果吻合较好,随着风速的继续增大,数值模拟结果和试验偏差也增大,但偏差仍在可接受的范围内。由此可以验证阶跃自激力模型能较好地模拟本文的π型叠合梁断面的气动自激力。在颤振的过程中,模型的竖弯和扭转频率一致,且随着风速的增大,耦合的频率逐渐减小,数值模拟得出了同样的结论,但数值模拟的频率减小的程度要低,耦合频率的结果如图 11所示。数值模拟的颤振临界风速结果和试验结果十分接近,结果的对比如图 12所示,三个攻角下试验和计算的误差分别为-5.50%,-2.39%和6.49%。试验和数值模拟的不完全一致可以归于为:
(1)试验颤振导数识别及阶跃函数拟合自身也会存在误差;
(2)试验悬挂系统的非线性阻尼与在数值计算中线性阻尼的差异;
(3)数值计算中没有考虑平均风攻角改变对气动自激力的影响,这种改变在试验中是存在的;
(4)气动导数会随着幅值的改变而改变。气动导数A_2^*受幅值影响最大[32],本文在数值计算中没有考虑气动导数随幅值的改变,因而扭转幅值比竖向幅值与试验偏差更大;
(5)节段模型在大振幅下会与来流形成较大的风攻角,这可能使风洞阻塞率增大,进而影响模型的后颤振响应。
3.3 结构阻尼比
相关规范[33]中,桥梁结构颤振临界风速的估算方法并没有直接考虑结构阻尼比的影响。结构的阻尼比是影响桥梁断面颤振临界极限环振动风速的重要因素[34],其对桥梁断面颤振临界风速的影响程度取决于气动阻尼大小,如果气动阻尼由正急剧变负,且远大于结构阻尼,则即使增大结构阻尼比,颤振临界风速也不会发生较大的改变。在接近颤振临界风速时,模型实际上是做幅值非常小的等幅振动,可以描述为临界极限环振动。在数值计算中,不同阻尼下的临界极限环振动幅值略有不同,具体如图13所示。从图中可知处于颤振临界状态下的临界极限环幅值较小,且竖向幅值在阻尼比ξ<0.011的情况下随阻尼比线性增加,然后其增长趋势放缓;而扭转幅值随阻尼比先增加后减小。
如图14所示,在+3°攻角的情况下,其颤振临界风速随阻尼比基本成线性关系,因此颤振临界风速对结构阻尼比较敏感。从图5中也可知,A_2^*项在折算风速U/(fB)小于6的区间内变化较小,同时数值也接近零,进而断面的气动阻尼较小,结构阻尼在系统总阻尼中占绝大部分,这间接说明了颤振临界风速和结构阻尼比基本成线性关系。由于在建造桥梁之前并不知道实际桥梁的真实阻尼比,在风洞试验中,一般依据《公路桥梁抗风设计规范》来选取不同类型桥梁的阻尼比,对于平板断面,在规范建议的阻尼比范围内,其颤振临界改变并不是很明显,然而对于π型叠合梁断面,这可能过高或过低估计桥梁的实际颤振临界风速。
利用本文数值模拟方法,可得不同阻尼比(竖弯阻尼比和扭转阻尼比相同)下随风速演变的后颤振LCO幅值,如图 15所示,从图中可知不同阻尼比下,竖向幅值和扭转幅值演变趋势不相同,阻尼比较小时,改變阻尼比对幅值演变趋势及幅值影响很大;当阻尼比较大时,改变阻尼比基本不会对后颤振演变趋势产生影响,只是幅值稍微变化;竖向幅值受结构阻尼比相对较小。
4 结 论
本文通过风洞试验研究了π型叠合梁断面的颤振幅值、频率及极限环特性,通过数值计算验证了自激力模型的可靠性,并基于阶跃函数的自激力模型对π型叠合梁断面进行了数值模拟,主要结论如下:
(1)风洞试验表明,π型叠合梁断面在颤振临界风速状态下以临界极限环振动,超过颤振临近风速后做幅值较大的LCO;数值计算表明,考虑几何非线性后,π型叠合梁断面的颤振形式并不是发散而是趋于稳定的颤振LCO。颤振试验结果和数值模拟吻合较好,验证了本文时域计算方法的可靠性。
(2)采用偽稳态自激力分离法成功地从阶跃函数气动自激力模型中扣除了平均响应引起的自激力部分,可成功处理传统气动力模型中的一些不兼容问题。
(3)π型叠合梁的颤振临界风速随阻尼比基本线性增加。这种对结构阻尼特性的依赖关系,表征了中国现有桥梁抗风规范的不足。
(4)不同阻尼比下的竖向幅值和扭转幅值演变趋势不一致;在低阻尼比下,较小的阻尼比变化对后颤振幅值和演变趋势影响大,而在较高的阻尼比下,后颤振的演变趋势基本一致,只是幅值轻微改变;竖向幅值受结构阻尼比影响相对较小。
参考文献:
[1] Larsen A, Walther J H. Aeroelastic analysis of bridge girder sections based on discrete vortex simulations[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1997, 67(97):253-265.
[2] Katsuchi H, Jones N P, Scanlan R H, et al. Multi-mode flutter and buffeting analysis of the Akashi-Kaikyo bridge[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1998, 77-78(5):431-441.
[3] Agar T J A. Aerodynamic flutter analysis of suspension bridges by a modal technique[J]. Engineering Structures, 1989, 11(2):75-82.
[4] Namini A, Albrecht P, Bosch H. Finite element-based flutter analysis of cable-suspended bridges[J]. Journal of Structural Engineering, 1992, 118(6):1509-1526.
[5] Diana G, Resta F, Zasso A, et al. Forced motion and free motion aeroelastic tests on a new concept dynamometric section model of the Messina suspension bridge[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2004, 92(6):441-462.
[6] Morse-Fortier L J. Professor Robert H Scanlan and the Tacoma Narrows Bridge[C]. Proceedings of the Structures Congress and Exposition, 2005:2367-2378.
[7] Schewe Günter, Mai Holger. Experiments on transonic limit-cycle-flutter of a flexible swept wing[J]. Journal of Fluids and Structures, 2019, 84(84):153-170.
[8] Amandolese X, Michelin S, Choquel M. Low speed flutter and limit cycle oscillations of a two-degree-of-freedom flat plate in a wind tunnel[J]. Journal of Fluids and Structures, 2013, 43:244-255.
[9] Zhang M, Xu F, Ying X. Experimental investigations on the nonlinear torsional flutter of a bridge deck[J]. Journal of Bridge Engineering, 2017, 22(8):04017048.
[10] 郑史雄,郭俊峰,朱进波,等. π型断面主梁软颤振特性及抑制措施研究[J].西南交通大学学报,2017,52(3):458-465.
Zheng S, Guo J, Zhu J, et al. Characteristic and Suppression neasures for soft flutter of main girder with π-shaped cross section[J]. Journal of Southwest Jiaotong University,2017,52(3):458-465.
[11] Ying X, Xu F, Zhang M, et al. Numerical explorations of the limit cycle flutter characteristics of a bridge deck[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2017,170:226-237.
[12] Ruzicka Martin, Horacek Jaromir, Svacek Petr, et al.Numerical analysis of flow-induced nonlinear vibrations of an airfoil with three degrees of freedom[J].Computers & Fluids,2011,49(1):110-127.
[13] Gharali K, Johnson D A. Dynamic stall simulation of a pitching airfoil under unsteady freestream velocity[J]. Journal of Fluids and Structures, 2013, 42:228-244.
[14] Wang S, Ma L, Ingham D B, et al. Turbulence modelling of deep dynamic stall at low Reynolds number[J]. Lecture Notes in Engineering & Computer Science, 2010, 2184(1):191-209.
[15] Tran C T, Petot D. Semi-empirical model for the dynamic stall of airfoils in view of the application to the calculation of responses of a helicopter blade in forward flight[J].Vertica, 1981,5(1):35-53.
[16] Sarkar S, Bijl H. Nonlinear aeroelastic behavior of an oscillating airfoil during stall-induced vibration[J]. Journal of Fluids and Structures, 2008, 24(6):757-777.
[17] Stanford B, Beran P. Direct flutter and limit cycle computations of highly flexible wings for efficient analysis and optimization[J]. Journal of Fluids and Structures, 2013, 36:111-123.
[18] Leishman J G, Beddoes T S. A semi-empirical model for dynamic stall[J]. Journal of the American Helicopter Society, 1986, 34(3):3-17.
[19] Leishman J G. Validation of approximate indicial aerodynamic functions for two-dimensional subsonic flow[J]. Journal of Aircraft, 1988, 25(10):914-922.
[20] Galvanetto U, Peiró J, Chantharasenawong C. An assessment of some effects of the nonsmoothness of the Leishman?Beddoes dynamic stall model on the nonlinear dynamics of a typical aerofoil section[J]. Journal of Fluids and Structures, 2008, 24(1):151-163.
[21] Larsen J W, Nielsen S R K, Krenk S. Dynamic stall model for wind turbine airfoils[J]. Journal of Fluids and Structures, 2007, 23(7):959-982.
[22] Diana G, Rocchi D, Argentini T, et al. Aerodynamic instability of a bridge deck section model: Linear and nonlinear approach to force modeling[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2010, 98(6-7):363-374.
[23] 王 骑, 廖海黎, 李明水, 等. 桥梁断面非线性自激气动力经验模型[J]. 西南交通大学学报, 2013, 48(2):271-277.
Wang Q, Liao H, Li M, et al. Empirical mathematical model for nonlinear motion-induced aerodynamic force of bridge girder[J]. Journal of Southwest Jiaotong University, 2013, 48(2):271-277.
[24] Wu T, Kareem A.A low-dimensional model for nonlinear bluff-body aerodynamics: A peeling-an-onion analogy[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2015, 146:128-138.
[25] 刘十一, 葛耀君. 非线性子系统的大振幅时域自激力模型[J]. 哈尔滨工业大学学报, 2015,(9):73-78.
Liu S, Ge Y. Nonlinear dynamic subsystem model for large-amplitude motion-induced aerodynamic forces of bridge decks[J]. Journal of Harbin Institute of Technology, 2015,(9):73-78.
[26] 朱乐东, 高广中. 双边肋桥梁断面软颤振非线性自激力模型[J]. 振动与冲击, 2016, 35(21):29-35.
Zhu L, Gao G. A nonlinear self-excited force model for soft flutter phenomenon of a twin-side-girder bridge section[J]. Journal of Vibration and Shock, 2016, 35(21):29-35.
[27] Gao G, Zhu L, Han W, et al. Nonlinear post-flutter behavior and self-excited force model of a twin-side-girder bridge deck[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2018, 177:227-241.
[28] Zhang M, Xu F, Zhang Z, et al. Energy budget analysis and engineering modeling of post-flutter limit cycle oscillation of a bridge deck[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2019, 188:410-420.
[29] 吴长青,张志田.平均风与气弹效应一体化的桥梁非线性后颤振分析[J].振动工程学报,2018,31(3):399-410.
Wu C, Zhang Z. Nonlinear post-flutter analysis of bridges decks with integrated mean and aero-elastic wind effects[J]. Journal of Vibration Engineering, 2018,31(3):399-410.
[30] Robert H Scanlan. Problematics in formulation of wind-force models for bridge decks[J]. Journal of Engineering Mechanics, 1993, 119(7):1353-1375.
[31] Zhang Z. Multi-stage indicial functions and post-flutter simulation of long-span bridges[J]. Journal of Bridge Engineering, 2018, 23(4):04018010.
[32] Noda M, Utsunomiya H, Nagao F, et al. Effects of oscillation amplitude on aerodynamic derivatives[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2003, 91(1-2):101-111.
[33] 中华人民共和国交通部. 公路桥梁抗风设计规范 [M]. 北京:人民交通出版社,2018
[34] Chen X, Kareem A. Efficacy of tuned mass dampers for bridge flutter control[J]. Journal of Structural Engineering, 2003, 129(10):1291-1300.
Experimental and numerical investigations on flutter of π-shaped side-girders
WANG Zhi-xiong1, ZHANG Zhi-tian2, WU Chang-qing1, QIE Kai1
(1. Wind Engineering Research Center, College of Civil Engineering, Hunan University, Changsha 410082, China;
2. College of Civil Engineering and Architecture, Hainan University, Haikou 570228, China)
Abstract: The flutter instability and flutter derivative tests are carried out with a sectional model of a π-shaped composite beam. The results show that the flutter of the section is limit cycle oscillation (LCO) rather than divergent vibration. The post-flutter LCO and its evolution with frequency are analyzed. A post-flutter self-excitation force model based on indicial function (IF) is employed and its accuracy and reliability in calculating the critical flutter wind speed and post-flutter amplitude are verified by experiments. The sources of errors between the experimental and the numerical results are analyzed. The role of geometric nonlinearity in post-flutter is studied, and the pseudo-steady separation method is adopted to deal with the repeated consideration of mean wind loads. The effects of different structural damping ratios on the critical wind speed and post-flutter amplitude are studied. It is revealed that the flutter and post flutter of the π section have great dependence on the structure damping. The numerical results show that the IFs self-excitation force model successfully realizes the time-domain analysis considering the average wind effect and geometric nonlinearity, which provides theoretical basis and solving strategy for the analysis of the nonlinear post-flutter performance of long-span bridges.
Key words: wind tunnel test; post-flutter; nonlinear; indicial function; limit cycle oscillation
作者簡介: 汪志雄(1994-),男,博士研究生。电话:18707497532;E-mail:doctorwzx@hnu.edu.cn
通讯作者: 张志田(1974-),男,博士,教授。电话:13975127541:E-mail:zhangzhitian@hnu.edu.cn

