混合润滑状态下结合面法向动态接触刚度与阻尼模型

李玲　裴喜永　史小辉　蔡安江　段志善

摘要： 机械结合面的动态接触特性对评估机床整机性能有着重要的意义。针对混合润滑状态下固定结合面复杂的接触特性，提出了一种结合面的法向接触刚度与阻尼模型。采用三维Weierstrass?Mandelbrot函数获得粗糙表面形貌，并基于分形理论建立了结合面固体部分的接触刚度与接触阻尼模型;根据平均流动的广义雷诺方程建立了液体油膜接触刚度与阻尼模型，其中油膜接触刚度是固体表面接触刚度的函数，实现了油膜接触刚度与固体接触刚度的耦合。通过仿真分析了固体、液体油膜以及结合面的刚度阻尼特性，结果表明：液体油膜接触阻尼远大于固体接触阻尼，结合面的接触阻尼特性主要取决于油膜接触阻尼;在接触前期油膜接触面积所占比例较大，结合面的接触刚度主要由油膜接触刚度主导，随着固体真实接触面积的增加，液体油膜接触刚度占结合面接触刚度的比率越来越小，最后转变为固体接触刚度主导结合面的接触刚度。

关键词： 结合面; 混合潤滑; 等效厚度; 接触刚度; 接触阻尼; 分形理论

中图分类号： TH113.1; TB123    文献标志码： A    文章编号： 1004-4523（2021）02-0243-10

DOI：10.16385/j.cnki.issn.1004-4523.2021.02.004

引  言

结合面是构成机床整机的关键组成部分，在机床结构件之间起着传递运动、载荷和能量的重要作用。研究表明，整个机床中，结合面的接触刚度约占机床总刚度的60%?80%[1]，结合面的接触阻尼占机床全部阻尼的90%以上[2]。因此，开展结合面刚度阻尼特性的研究对整机性能的预测至关重要。

机械结构中的结合面可等效为两个粗糙表面的接触，国内外学者已对粗糙表面的接触问题进行了广泛的研究[3?6]，但仍然存在很多问题。其中应用最广泛的接触模型是Greenwood和Williamson[7]提出的统计学接触模型（GW模型），GW模型将单个刚性球体与弹性半空间的接触扩展为一个刚性平面与一个粗糙表面间的接触，通过统计学方法分析了多种因素对结合面的影响规律，但该模型中采用的统计学参数会受到测量仪器分辨率的影响[8]，使得测量结果具有尺寸依赖性。因此，建立一种能够将所有尺度的粗糙度信息都包含于其中的粗糙表面表征模型具有重要的意义。

Mandelbrot等[9?10]首先发现，Weierstrass?Mandelbrot函数（W?M函数）处处连续且不可微，具有统计自仿射特性，很适合用来表征粗糙表面的表面轮廓，避免了统计学模型受测量仪器分辨率的影响。Majumdar和Bhushan[11?12]基于W?M函数将分形几何理论应用于两粗糙表面间的接触分析，认为粗糙表面形貌具有自相似性和尺度独立性，建立了一种新的结合面分形接触模型（MB模型）。为了进一步完善分形接触模型，W?M函数也被用于建立考虑微凸体弹性变形，弹塑性变形以及塑性变形的各个分析模型中[13?15]，且有大量学者基于分形模型研究了结合面法向与切向的接触刚度阻尼特性[16?19]。但是，上述关于结合面的研究中仅限于干摩擦条件下的粗糙表面接触，获得的法向接触刚度与接触阻尼模型尚不能用于混合润滑状态下结合面的刚度阻尼特性分析。

实际上，机床中大部分结合面在工作中往往都处于混合润滑状态[20]，此时，结合面间同时存在油膜和微凸体的接触。关于混合润滑状态下结合面接触刚度与阻尼的研究，李小彭等[21]将梁结构及它们之间的结合面重构为固体?广义间隙?固体系统，利用结合面接触刚度的分形模型与材料应变能等效的方法，获得了结合面广义间隙的材料常数，并验证了结合面接触刚度分形模型的正确性。Li等[22]采用双变量W?M函数表征粗糙表面形貌，利用表面粗糙度来计算油膜等效厚度，建立了考虑表面形貌影响的结合面接触阻尼模型，分析了表面粗糙度对挤压油膜阻尼特性的影响规律。李昌等[23]基于Dowson最小膜厚公式，给出了弹流油膜刚度的解析表达式。

然而，上述关于混合润滑结合面的理论接触模型都假设油膜等效厚度为一定值，且缺乏完整的混合润滑状态下结合面的接触刚度与阻尼模型。为此，本文基于分形理论建立了结合面固体接触刚度与接触阻尼模型，利用固体弹性接触刚度获得了变化的油膜等效厚度。根据平均流动的广义雷诺方程获得了润滑油膜的接触刚度与接触阻尼。最后，基于载荷分配的思想，建立了混合润滑状态下固定结合面的法向接触刚度与接触阻尼模型。该模型考虑了油膜等效厚度的变化，对结合面的润滑设计以及润滑状态预测具有重要的理论指导意义。

1 三维粗糙表面形貌表征

传统的表面形貌表征采用的是轮廓算术平均值Ra、轮廓高度均方根值σ等统计学参数，但这些统计学参数受测量仪器分辨率的影响，只能反映测量仪器分辨率和采样长度相关的粗糙度信息。因此，本文采用具有自相似性和尺寸独立性的分形几何参数来表征粗糙表面形貌[24]，其可表示为

2 混合润滑结合面的并联接触模型

对于混合润滑的固定结合面，既存在微凸体的接触，又存在润滑剂的接触，此时，结合面间的法向载荷由润滑剂与固体共同承担[25]。研究该类结合面的刚度阻尼特性可以转化为研究固体接触的刚度、阻尼特性以及挤压油膜的刚度、阻尼特性。

两粗糙表面的接触可以等效为一刚性平面与一等效粗糙表面的接触，混合润滑状态下，它们之间的间隙由润滑剂填充，如图2（a）所示。此时，根据载荷分配思想将结合面接触刚度Kt等效为固体接触刚度Ks与液体油膜接触刚度Kl的并联连接模型，同理，结合面的接触阻尼Ct也可等效为固体阻尼Cs与油膜阻尼Cl的并联模型，如图2（b）所示。

5 结果与分析

5.1 模型验证

不同接触模型下结合面接触刚度随法向载荷的变化规律如图4所示。表面材料属性参数E*=2×1011 Pa，H=0.65 GPa[33];润滑油选用46#液压油，其黏度值在常温下为0.018 Pa?s，其他仿真参数D=2.35，G=1×10-12 m，η空气=1.81×10-5 Pa?s（常温下）。由图可知，利用本文模型、YK模型[24]以及WXL模型[34]获得的数值解具有一致性，这说明了本文模型的合理性。值得注意的是当两粗糙表面处于干摩擦接触状态时，润滑介质为空气，本文模型与YK模型基本重合;当润滑介质为油时，接触刚度随着法向载荷的增大呈先减小后增大的趋势，最后与干摩擦模型重合。这是因为在接触前期结合面的接触刚度主要由油膜接触刚度主导，之后随着载荷的增加，结合面间隙中的油膜由于挤压作用发生侧漏或回渗到固体中，油膜接触刚度占结合面接触刚度的比率逐渐减小，当载荷增大到一定程度时，结合面的接触刚度开始由固体接触刚度主导，逐渐向边界润滑状态转化。

5.2 润滑油膜等效厚度的变化规律

选用D=2.4，G=1×10-12 m的表面分形参数，其他仿真计算参数如表1所示，分析了液体油膜等效厚度随法向压力的变化规律，结果如图5所示。由图可知，润滑油膜等效厚度随着法向压力的增大而减小，且其递减速率先快后慢，二者呈非线性的关系。这是因为当表面粗糙度一定时，法向压力的增大使得固体的真实接触面积以先快后慢的速率递增;相反地，结合面间隙中的油膜接触面积以先快后慢的速率递减，从而引起油膜等效厚度的减小。

5.3 分形参数对固体真实接触面积、接触刚度以及接触阻尼的影响

固体真实接触面积大小的主要影响因素是分形参数和法向载荷，载荷一定时，真实接触面积与分形维数D、分形粗糙度G的关系如图6所示。由图可知，当D不变时，Ar随着G的增大而减小，即表面越粗糙，真实接触面积越小。同时也观察到，随着D的增加，Ar呈先增大后减小的趋势，这说明了存在一个最优的分形维数D，使得固体的真实接触面积达到一个最大值。

图7表示不同分形参数下固体接触刚度与真实接触面积的关系曲线。由图可知，固体接触刚度Ks随着真实接触面积的增大而增大，同时，从图7（a）中可以发现，当固体真实接触面积一定时，分形维数D越大，接触刚度Ks越大。相反地，由图7（b）可知，真实接触面积一定时，接触刚度Ks随着分形粗糙度参数G的增大而减小。分形维数D的增大与分形粗糙度参数G的减小都可以减小表面的粗糙度，这意味着较小的表面粗糙度有助于改善结合面的接触刚度特性。

不同分形粗糙度参数下固体接触阻尼损耗因子ψ随分形维数D的变化规律如图8所示。从图中观察到，ψ随着D的增大呈先减后增的变化趋势，整个阻尼损耗因子的变化曲线呈下凹的函数特性。在D=2.35附近阻尼损耗因子达到了最小，之后随着D的增大，分形粗糙度参数对阻尼损耗因子的影响越来越小，直到D>2.7以后，阻尼损耗因子几乎不受分形粗糙度参数的影响，此时不同分形粗糙度参数下的损耗因子基本相等。同时，当分形维数D一定时，分形粗糙度参数G越大，阻尼损耗因子越大，即表面越粗糙，阻尼损耗因子越大。

图9表示不同分形粗糙度参数下固体接触阻尼与分形维数D的关系曲线。由图可知，固体接触阻尼Cs随分形维数D的变化规律与图8中阻尼损耗因子的变化规律基本一致，都呈先减小后增大的变化趋势。同时发现，在D=2.3附近，接触阻尼达到了最小，之后随着分形维数的增加，接触阻尼曲线在D=2.55处出现了拐点;当D<2.55时，接触阻尼随着分形粗糙度参数G的增大而增大;当D>2.55时，随着分形粗糙度参数G的增大，接触阻尼反而呈减小的变化趋势。

5.4 分形参数对液体油膜接触刚度的影响

与固体接触部分的接触刚度仿真类似，液体油膜接触刚度Kl在不同分形参数下随固体真实接触面积的变化规律如图10所示。从图中可以看出，当固体的真实接触面积增大时，液体油膜接触刚度Kl逐渐减小，这是由于固体真实接触面积增大时，液体油膜接触面积所占比例减小，进而导致液体油膜的接触刚度Kl减小。同时，Kl随分形维数D和分形粗糙度参数G的变化规律与固体接触刚度的变化趋势一致。

5.5 混合润滑状态下结合面的接触刚度与接触阻尼

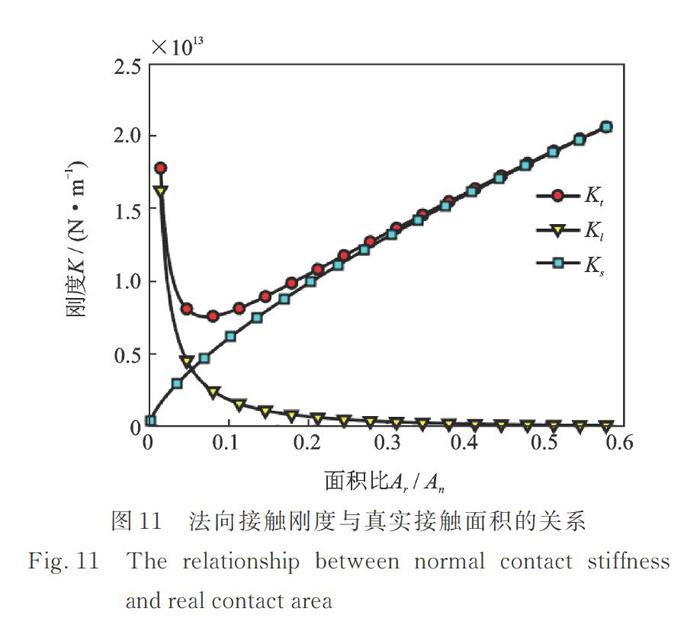
图11表示结合面接触刚度Kt、油膜接触刚度Kl以及固体接触刚度Ks与真实接触面积的关系。从图中观察到，结合面的接触刚度随着真实接触面积的增加呈先减小后增加的趋势，大概在真实接触面积占名义接触面积的10%附近，结合面接触刚度曲线出现了拐点，刚度值达到了最小。研究表明，结合面固体真实接触面积仅占名义接触面积的一小部分，即使是高精度的机加工表面，真实接触面积仅占名义接触面积的10%?20%，这恰好是图11中结合面接触刚度的拐点位置。同时，从图中还可以看出，当Ar/An<10%时，油膜刚度占主导作用，此时油膜接触所占面积较大，结合面间接近于流体润滑，结合面的接触刚度相当于油膜的静压刚度。因此，结合面的接触刚度在接触前期较大，之后，随着固体真实接触面积的增加，油膜接触部分所占比例减小，固体接触刚度的作用变得越来越明显，油膜接触刚度占结合面接触刚度的比率逐渐减小。

表面粗糙度和载荷是影响结合面固体真实接触面积的两大主要因素，当载荷一定时，表面粗糙度越小，真实接触面积越大。通过对比结合面的接触刚度与固体接触刚度可知，在不改变表面粗糙度（甚至降低）的情况下，如图中10%左右，添加润滑油可有效提高结合面的接触刚度。

结合面法向接触阻尼Ct在不同分形维数D下随法向载荷Ft的变化规律如图12所示。由于液体油膜接触阻尼远大于固体接触阻尼，所以液体油膜接触阻尼主导着结合面的接触阻尼。从图中可以觀察到，结合面接触阻尼与法向总载荷呈非线性的关系，且其随着法向载荷的增大而减小，这是因为当表面粗糙度不变时，固体真实接触面积随着载荷的增大而增大，此时，油膜由于挤压作用发生侧向泄漏或者回渗到固体中，油膜接触面积所占比例减小，结合面处于贫油状态，从而引起结合面接触阻尼的减小。同时，从图中还可获得，表面越光滑，结合面接触阻尼越大。

6 结  论

机床中的结合面普遍采用添加润滑剂的方式降低摩擦系数，减少表面磨损，提高机床的使用寿命和精度保持性。本文基于混合润滑状态下固定结合面法向载荷由固体与润滑剂共同承担的载荷分配思想，分别建立了结合面接触刚度和接触阻尼的并联连接模型，仿真分析了结合面的刚度阻尼特性，为评估机床整机的动态性能提供了帮助。

（1） 针对混合润滑状态下结合面间变化的油膜厚度，利用固体接触部分的弹性接触刚度求解了液体油膜的等效厚度，实现了固体表面接触刚度和液体油膜接触刚度的耦合。

（2）在接触前期，结合面固体真实接触面积较小，液体油膜接触面积所占比例较大，结合面的接触刚度主要由油膜接触刚度主导，随着真实接触面积的增加，液体油膜接触刚度占总刚度的比率越来越小，固体接触刚度作用变得明显，最后转变为固体接触刚度主导结合面的接触刚度。

[16] CHEN Q， XU F， LIU P， et al. Research on fractal model of normal contact stiffness between two spheroidal joint surfaces considering friction factor[J]. Tribology International， 2016， 97： 253-264.

[17] 李小彭，王 雪，運海萌，等.三维分形固定结合面法向接触刚度的研究[J].华南理工大学学报（自然科学版）， 2016， 44（1）： 114-122.

LI X， WANG X， YUN H， et al. Investigation into normal contact stiffness of fixed joint surface with three-dimensional fractal[J]. Journal of South China University of Technology （Natural Science Edition）， 2016， 44（1）： 114-122.

[18] JIANG S， ZHENG Y， ZHU H. A contact stiffness model of machined plane joint based on fractal theory[J]. Journal of Tribology， 2010， 132（1）： 11401.

[19] ZHANG X， WANG N， LAN G， et al. Tangential damping and its dissipation factor models of joint interfaces based on fractal theory with simulations[J]. Journal of Tribology， 2014， 136（1）： 11704.

[20] LIU J， SHAO Y. An improved analytical model for a lubricated roller bearing including a localized defect with different edge shapes[J]. Journal of Vibration and Control， 2018， 24（17）： 3894-3907.

[21] 李小彭，梁亚敏，郭 浩，等.结合面广义间隙的等效模型研究[J].振动工程学报， 2014， 27（1）： 25-32.

Li Xiaopeng， Liang Yamin， Guo Hao， et al. Study on equivalent model of generalized clearance of joint surface[J]. Journal of Vibration Engineering， 2014， 27（1）： 25-32.

[22] LI L， YANG J， LIU W. Effect of random surface roughness on squeeze film damping characteristics in damper of linear rolling guide with a fractal-based method[J]. Industrial Lubrication and Tribology， 2015， 67（6）： 549-556.

[23] 李 昌，孙志礼.基于弹流润滑理论的深沟球轴承动态虚拟仿真[J].航空动力学报， 2009， 24（4）： 951-956.

LI Chang， Sun Zhili. Dynamic virtual simulation of deep groove ball bearing： Based on elastohydrodynamic lubrication theory[J]. Journal of Aerospace Power， 2009， 24（4）： 951-956.

[24] YAN W， KOMVOPOULOS K. Contact analysis of elastic-plastic fractal surfaces[J]. Journal of Applied Physics， 1998， 84（7）： 3617-3624.

[25] JOHNSON K L， GREENWOOD J A， POON S Y. A simple theory of asperity contact in elastohydro-dynamic lubrication[J]. Wear， 1972， 19（1）： 91-108.

[26] BORODICH F M. The Hertz frictional contact between nonlinear elastic anisotropic bodies （the similarity approach）[J]. International Journal of Solids and Structures， 1993， 30（11）： 1513-1526.

[27] 田红亮，郑金华，赵春华，等. 界面损耗因子与法向阻尼的计算方法[J]. 上海交通大学学报， 2015， 49（5）： 687-695.

Tian Hongliang， Zheng Jinhua， Zhao Chunhua， et al. Calculating method of surface dissipation factor and normal damping[J]. Journal of Shanghai Jiao Tong University， 2015， 49（5）： 687-695.

[28] 尤晋闽，陈天宁. 结合面法向动态参数的分形模型[J]. 西安交通大学学报， 2009， 43（9）： 91-94.

You Jinmin， Chen Tianning. Fractal model for normal dynamic parameters of joint surfaces[J]. Journal of Xi'an Jiaotong University， 2009， 43（9）： 91-94.

[29] WANG X， WEN S， GUI C. A generalized Reynolds equation based on the average flow model[J]. Lubrication Engineering， 1998， 3： 16-18.

[30] PATIR N， CHENG H S. An average flow model for determining effects of three-dimensional roughness on partial hydrodynamic lubrication[J]. Journal of Lubrication Technology， 1978， 100（1）： 12-17.

[31] GONZALEZ-VALADEZ M， DWYER-JOYCE R S， LEWIS R. Ultrasonic reflection from mixed liquid-solid contacts and the determination of interface stiffness[J]. Tribology and Interface Engineering Series， Elsevier， 2005，48： 313-320.

[32] 周桂如. 流體润滑理论[M]. 杭州：浙江大学出版社， 1990.

Zhou Guiru. Fluid Lubrication Theory[M]. Hangzhou： Zhejiang University Press， 1990.

[33] PAN W， LI X， WANG L， et al. Influence of contact stiffness of joint surfaces on oscillation system based on the fractal theory[J]. Archive of Applied Mechanics， 2018， 88（4）： 525-541.

[34] PAN W， LI X， WANG L， et al. A normal contact stiffness fractal prediction model of dry-friction rough surface and experimental verification[J]. European Journal of Mechanics-A/Solids， 2017， 66： 94-102.

Normal dynamic contact stiffness and damping model of joint surfaces in mixed lubrication

LI Ling， PEI Xi-yong， SHI Xiao-hui， CAI An-jiang， DUAN Zhi-shan

（School of Mechanical and Electrical Engineering， Xi'an University of Architecture and Technology， Xi'an 710055， China）

Abstract： The dynamic characteristic of joint surfaces is of great significance for evaluating the performance of machine tools. In this paper， a normal contact stiffness and damping model of joint surfaces are proposed for studying the complicated contact characteristics of fixed joint surfaces in mixed lubrication. Firstly， the three-dimensional Weierstrass-Mandelbrot function is used to describe the rough surface， and the solid contact stiffness and damping model is established based on the fractal theory. Then， the contact stiffness and damping model of the lubricant are established based on the mean flow generalized Reynolds equation， in which the lubricant contact stiffness is a function of the solid contact stiffness. Finally， the contact stiffness and damping of the solid part， lubricant part and the joint surfaces are analyzed. The results show that the damping of the lubricant film is much larger than that of the solid part， and the contact damping of joint surfaces is mainly dominated by the damping of the lubricant film. The contact stiffness of joint surfaces is dominated by the lubricant contact stiffness in the early stage of contact. However， the ratio of the lubricant contact stiffness to the stiffness of joint surfaces decreases with increasing the real contact area. At last， the solid contact stiffness dominates joint surfaces.

Key words： joint surface; mixed lubrication; equivalent thickness; contact stiffness; contact damping; fractal theory

作者简介： 李  玲（1981-），男，教授。E-mail： liling@xauat.edu.cn

通讯作者： 史小辉（1977-），男，讲师。E-mail： 13811382617@163.com