两自由度平板大幅运动的气动特性与稳定性的CFD研究
祝志文 颜爽 王钦华 李加武

摘要: 为研究两自由度薄平板大幅运动的气动特性,评价其气动稳定性,基于任意拉格朗日?欧拉描述法的动网格技术,通过有限差分法求解描述任意流变区域不可压流动的控制方程,开展了不同折减风速下薄平板竖弯和扭转运动绕流场的CFD (Computational Fluid Dynamics)模拟。研究认为,单自由度薄平板小幅运动的气动力系统是线性和稳定的,即使单自由度大幅竖弯运动也是线性和气动稳定的。但单自由度大幅扭转运动的平板气动力系统出现非线性,并随折减风速的提高非线性变得显著,且平板将进入气动不稳定状态。另外,大幅扭转耦合不同竖弯振幅运动的平板,气动力系统均为非线性并随折减风速的提高越加显著,而该非线性主要来自扭转自由度的大幅运动;对该两自由度耦合系统,当竖弯振幅较小和折减风速较高时,气动力系统是不稳定的;但当竖弯振幅较大时,气动力系统将是稳定的。
关键词: 气动稳定性; 薄平板; 大幅运动; CFD; 气动力非线性
中图分类号: U448.21+3; V211.3 文献标志码: A 文章编号: 1004-4523(2021)02-0271-12
DOI:10.16385/j.cnki.issn.1004-4523.2021.02.007
引 言
桥梁跨径的不断增大使得结构的频率和阻尼不断降低,导致桥梁对自然风作用的敏感程度明显增加,因而可能引起桥梁主梁的大幅运动。这些大幅运动,包括主梁的大幅涡激运动[1]和颤振[2],以及拉索的大幅振动[3?4]。对钝体外形的桥梁主梁,或主梁因大幅运动产生较大的相对攻角效应,桥梁主梁的气动力系统可能会因这种大幅运动而呈现显著的非线性[5?6]。开展桥梁主梁大幅竖弯和扭转运动下的气动特性研究,有助于评价现有线性气弹理论的应用条件和不足,有利于揭示桥梁大幅运动气动力系统的非线性特征和影响因素,以及桥梁气动稳定性的影响因素[7]。
在风洞中开展桥梁主梁大幅竖弯和扭转运动试验,存在试验驱动机构设计和布置、测力和测压、模型保护等诸多困难,而基于CFD开展这一研究,不仅能克服上述困难,还能方便地设置运动参数和边界条件,具有风洞试验无法相比的优势。当基于CFD开展桥梁主梁的大幅运动模拟时,因主梁周围空气所占据的实际空间随时间在发生显著的变化,具有大幅运动的边界,对此类显著流变区域流体的描述,需采用任意拉格朗日?欧拉描述法[8]。下面以桥梁气弹研究常采用的薄平板为研究对象,研究其大幅运动的气动特征和气动稳定性。
1 薄平板强迫运动绕流场控制方程
基于二维流体运动的任意拉格朗日?欧拉描述方程[8],通过建立计算域和物理域的随时间变化的映射关系,可在不随时间变化的二维计算域上,采用欧拉描述法实现对二维物理域上任意时变区域的流体流动的描述。根据桥梁主梁刚性断面的事实,以及主梁竖弯和扭转运动的特点,可简化得到薄平板强迫运动绕流场控制方程。
如图1所示为大幅运动的薄平板,设OXY表示绝对参考系下的直角坐标系,并用oxy表示随平板一起做刚性运动的动参考系下的直角坐标系,平板具有绕平衡位置的竖向自由度和绕转动轴的扭转自由度。设平板竖向运动速度为V0,绕通过其中点垂直于OXY平面轴的扭转角速度为ω(t)=dψ(t)/dt。对薄平板上述给定的两自由度运动,其对应的任意拉格朗日?欧拉描述方程可简化为动参考系下关于原参变量u,v和p的N?S方程[9],也即:
3.2 平板竖弯和扭转运动CFD模拟方法验证
为验证薄平板竖弯或扭转运动CFD模拟数值方法的合理性,本文以非定常气动力模拟为依据,通过有解析解的薄平板颤振导数Theodorsen解析解与本文识别结果的对比,验证本文方法的合理性。对竖弯或扭转运动的二自由度运动薄平板,其受到的非定常气动力作用可用八个颤振导数来表达[11?12],即:
式中 k=2πfb/U_0为折减频率;H_i^*和A_i^* (i=1?4)是颤振导数。
在不同折减风速下开展CFD计算,将分别得到作用在竖弯和扭转运动薄平板上的气动力,利用式(18)和(19)并通过最小二乘法可识别平板对应折减风速下的八个气动导数。本文CFD模拟首先开展了网格无关性检查,检查对象是颤振导数中相对重要的A_2^*导数在折减风速为4,8和12上的值,物面第一个网格高度分别取0.0005b,0.001b和0.002b三种情况,将计算结果与Theodorsen解析解对比表明,在0.0005b和0.001b两种情况下得到的结果与解析解一致性最好,也好于0.002b的情况。从非定常计算较大的计算量上考虑,本文CFD计算平板物面第一个网格高度取0.001b。
如图4所示,将本文识别的颤振导数和平板Theodorsen解析解作了比较。可见在低折减风速下,二者吻合很好;随着折减风速的增大,二者出现较小偏差。偏差的原因可能是解析解是基于无黏、无流动分离的势流理论,但本文是真实的有黏空气流动,且平板运动会导致流动分离,而黏性效应和流动分离可能随折减风速的增大而影响显著。本文识别结果与Theodorsen解析解[13]趋势性非常一致,这说明本文数值模拟能有效地获得运动薄平板上作用的气动力,因而能用于研究運动薄平板的气动力和能量特征。
3.3 单自由度小幅运动
为便于对比平板大幅运动的气动力和能量特征,下面给出Vr=8下,平板分别作小幅竖弯(振幅为B/80)或小幅扭转运动(振幅0.2°)的气动力时程。图5(a)和(b)分别是从多个气动力周期中取出一个完整周期(每个周期气动力完全相同),对应平板单自由度竖弯或单自由度扭转运动气动力系数时程曲线,可见无论是升力还是扭矩系数,其曲线具有明显的谐波特性,其时程频率等于扭转强迫运动频率。因此当平板单自由度小幅运动时,其气动力系统具有良好的线性特性。
图6为薄平板单自由度小幅扭转运动在一个周期内4个关键时刻的风压拓扑图,对应从平衡位置出发后达到最大正攻角位置(图6(a)),然后回到平衡位置(图6(b)),再达到最大负攻角位置(图6(c)),最后回到零攻角的平衡位置(图6(d))。可见从一个状态到另外一个状态,压力呈现规律性变化,反映了平板扭转运动方向的改变。平板前缘为风压值大和梯度高的区域,后缘为低风压区且压力变化远不及前缘剧烈。
图7(a)和(b)是在不同折减风速下竖弯运动的平板,一个周期内气流分别在平板上表面各点、以及整个平板上所做的无量纲总功。可见气流对平板表面所有点均做负功,也即平板表面均消耗气流能量,前缘(L.E.)局部耗能最强,后缘(T.E.)耗能最弱。图7(b)给出了Vr=8?60,竖弯运动平板一个周期内气流作用总功随折减风速的变化。从能量的角度可见,单自由度小幅竖弯运动的平板是气动稳定的。
图8(a)和(b)分别为单自由度小幅扭转运动的平板,一个周期内气流在平板上表面各点、以及整个平板所做的无量纲总功。从图8(a)可见平板前缘为稳定区,其后到转动轴(A.R)为不稳定区,也即气流对平板做正功,平板从气流中吸收能量,因此为激励区;转动轴到平板后缘气流做负功,因而是耗散气流能量的稳定区,此时平板上激励区与稳定区共存。图8(b)给出了Vr=8?60,一个扭转周期内气流对平板所做的总功,可见在所计算的折减风速范围内,一个周期内气流对扭转运动的平板均做负功,也即平板消耗气流的能量,因此单自由度小幅扭转运动的平板也是气动稳定的。
3.4 单自由度大幅运动
为研究薄平板单自由度大幅运动的气动特性,需对竖弯或扭转自由度方向设定远大于上述单自由度小幅运动的幅值。根据文献[7]对桥梁断面气动力非线性特性的研究结果,本文研究中,取大幅竖弯振幅为B/4,大幅扭转振幅为20°,以研究其气动力的线性特征和气动稳定性。
3.4.1 单自由度大幅竖弯运动(LAH)
图9(a)和(b)分别给出Vr=12和Vr=40时,分别从多个气动力周期时程中,取出一个完整周期(每个周期气动力完全相同),对应单自由度大幅竖弯运动的气动力时程。可见虽然折减风速差别大,但升力和扭矩系数时程的相位差变化不明显,特别是升力和扭矩系数时程曲线均具有较好的谐波特性,也即没有观察到明显的气动力非线性,因此可以认为,大幅竖弯运动的薄平板气动力系统的非线性不明显。
图10(a)和(b)分别是在一个周期内,气流在大幅竖弯运动平板上表面各点、以及对整个平板所做的无量纲总功。可见气流对竖弯运动的平板表面所有点均做负功,且随着折减风速的提高,功的绝对值虽越来越小,但仍为负。同时,在全部折减风速上,气流对整个平板所做的无量纲总功也均为负。因此,在本文所考虑的较大折减风速范围内,一个周期内气流对大幅度竖弯运动的平板均做负功,也即消耗气流的能量,因此单自由度大幅竖弯运动的平板是气动稳定的。
3.4.2 单自由度大幅扭转运动(LAP)
考察大幅扭转运动的情况,图11(a)和(b)分别为折减风速Vr=8和Vr=40时,分别从多个气动力周期时程中,取出一个完整周期(每个周期气动力完全相同),该周期内的气动力系数时程曲线。与图9相比,可见随着折减风速的提高,升力和扭矩系数间相位逐渐变化,且时程曲线波形发生畸变,也即失去谐波特性,特别是高折减风速下气动力时程曲线的畸变更顯著。对低和高折减风速下气动扭矩系数时程的归一化功率谱分析表明,在低折减风速下扭矩系数时程的频率等于扭转运动频率,如图12(a)所示;但高折减风速下扭矩系数时程虽然峰值频率为扭转运动频率,但频谱图中明显出现了倍频成分,如图12(b)所示,且倍频成分的能量明显小于扭转运动频率对应峰值能量,可见出现的非线性不是特别显著。因此,当薄平板大幅扭转运动时,其气动力系统不再为线性,且随着折减风速的提高,其非线性将越来越显著。这可能是折减风速增大,绕薄平板流动的分离加剧,因此平板表面的流态随着折减风速的提高在不断改变,使得气动力的非线性变得明显。
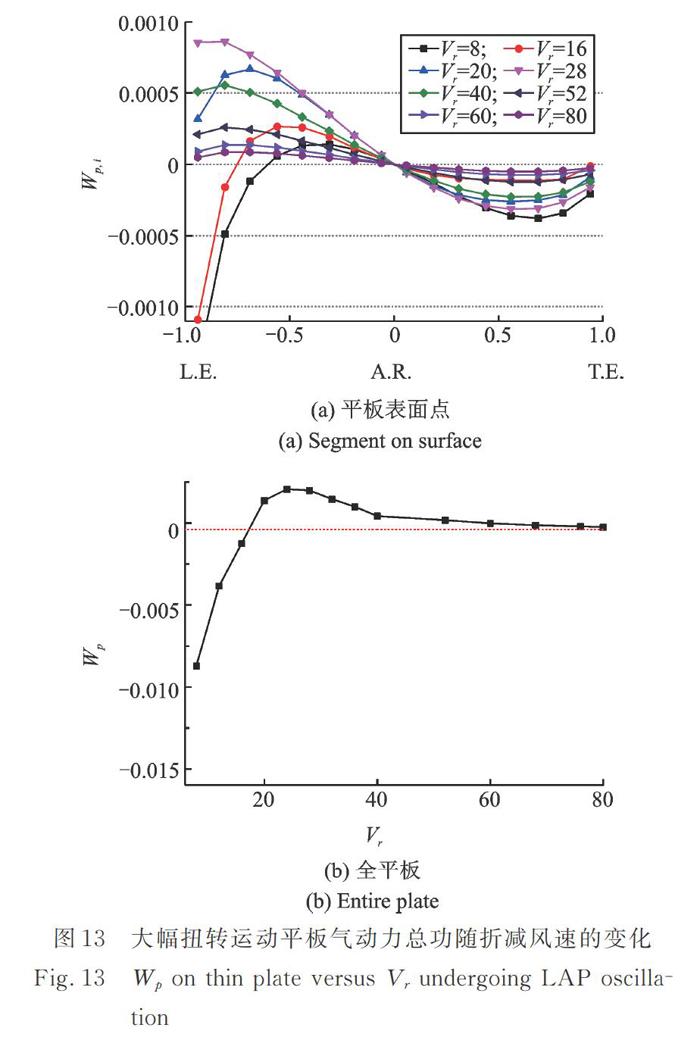
图13给出了一个扭转运动周期内气流对平板所做无量纲总功随折减风速的变化,可见当折减风速小于16时,一个周期内气流对平板所做总功为负,也即平板消耗气流的能量;但当折减风速大于20后,气流对上游侧半个平板估的正功将大于对下游侧半个平板所做负功,气流对平板所做的总功由负变为正,此时一个周期内扭转运动平板将从气流中吸收能量,表明大幅扭转运动平板已进入气动不稳定状态。
3.5 两自由度耦合运动
从上面研究可知,当扭转运动幅值角为20°且折减风速较高后,单自由度大幅扭转运动的薄平板将进入气动不稳定状态。下面针对扭转运动幅值角20°的情况,考察不同竖弯运动幅值平板两自由度耦合系统的气动特征,竖弯幅值分别采用小幅、中幅和大幅,对应的幅值分别是B/50,B/16和B/4,并设定耦合运动的竖弯和扭转自由度相位角为0o(CFD可设定任意相位角)。分别开展不同折减风速的CFD模拟,比较作用在平板上的气动力和一周期内气流对平板做功的能量特征。
3.5.1 小幅竖弯大幅扭转(SAH?LAP)
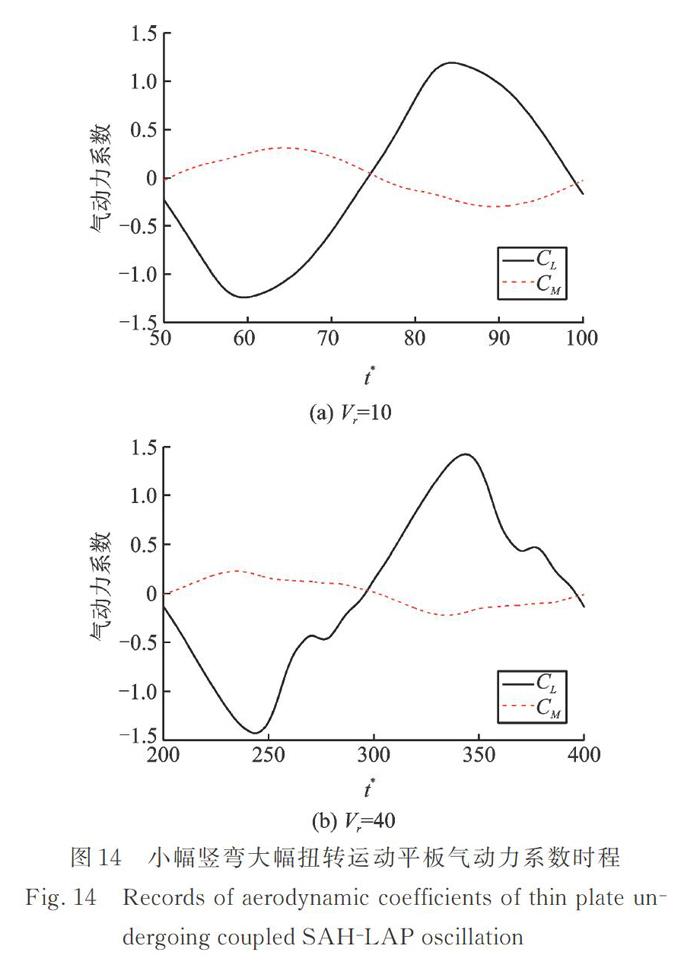
图14(a)和(b)分别是折减风速Vr=10和Vr=40时,从各自多个气动力周期时程中,取出一个完整周期(每个周期气动力完全相同),对应小幅竖弯大幅扭转运动平板一个周期内的气动力系数时程曲线。可见耦合运动平板的气动力系统表现出非线性,且随着折减风速的提高,其非线性特性越来越显著,其特征与图11相似。
图15给出了两个折减风速下耦合运动薄平板,在一个周期内气流在运动平板上表面各点所做的无量纲总功。可见每个自由度方向气流作用的能量特征与单自由度类似,也即竖弯自由度方向平板表面点均消耗气流能量,但扭转自由度方向是迎风侧上半个平板吸收气流能量,下游侧半个平板消耗气流能量。当折减风速较高时,上游侧半个平板吸收的能量明显大于下游侧半个平板消耗的能量,导致扭转自由度方向吸收气流能量。如综合两个自由度方向的总能量,在低折减风速下竖弯自由度消耗气流的能量大于扭转自由度吸收的能量,因此平板是气动稳定的;但当折减风速较高后,竖弯自由度消耗气流的能量小于扭转自由度方向吸收的能量,此时两自由度耦合运动系统是气动不稳定的,如图16所示。从图15也可见,由于竖弯自由度振幅小,其消耗的气流能量小,因此气流在扭转自由度方向作用的能量主导了两自由度耦合运动系统气流作用的总能量。
3.5.2 中幅竖弯大幅扭转(MAH?LAP)
维持薄平板两自由度运动的扭转幅值角为20°,并将竖弯运动位移幅值增大到B/16。图17给出了折减风速分别是Vr=10和Vr=40时,分别从多个气动力周期时程中,取出一个完整周期(每个周期气动力完全相同),对应一个周期内薄平板的升力和扭矩系数时程。可见即使低折减风速,薄平板气动力的谐波特性变差,而随着折减风速的提高,气动力时程的非线性特性越加显著。
图18给出了高低两个折减风速下耦合运动的薄平板,一个周期内气流在运动平板上表面各点所做的无量纲总功。其曲线特征与图15相似,也即竖弯自由度方向平板表面所有点均消耗气流能量,但扭转自由度方向是迎风侧上半个平板吸收气流能量,下游侧半个平板消耗气流能量。但由于竖弯自由度方向的振幅增大,竖弯运动消耗气流的能量明显增大,从两个自由度方向的能量总和来看,在所有折减风速下,平板均消耗气流的能量,如图19所示。因此,以中幅竖弯大幅扭转运动的薄平板是气动稳定的。与前述小幅竖弯大幅扭转运动情况相比,可见竖弯幅度的增大提高了平板的气动稳定性。
3.5.3 两自由度耦合大幅运动(LAH?LAP)
进一步增大竖弯运动幅值到B/4,使得两个自由度方向均为大幅运动,也即大幅耦合运动。图20给出了折减风速分别是Vr=10和Vr=40时,分别从多个气动力周期时程中,取出一个完整周期(每个周期气动力完全相同),对应薄平板一个周期内大幅耦合运动的升力和扭矩系数时程。可见气动力的非线性明显,也随折减风速的增大而显著。与图17相比,相同的折减风速下气动力的非线性并没有明显变化。
图21为低折减风速(Vr=10)和高折减风速(Vr=40)下大幅耦合运动的薄平板,一个运动周期内气流在运动平板上表面各点所做的无量纲总功。竖弯和扭转运动气流作用能量沿平板表面的分布与图18稍有不同,可能是两自由度大幅耦合运动导致。但因竖弯自由度方向的大幅运动,导致竖弯自由度方向消耗气流的能量大幅度增加,使得一个周期内气流对平板表面所有点均做负功,因此气流作用在运动平板上的总能量为负,并明显大于图16小幅竖弯大幅扭转和图19中幅竖弯大幅扭转运动的情况,如图22所示,因此大幅耦合运动的平板是气动稳定的,原因是竖弯自由度方向的振幅增大,显著提高了其气动稳定性。
4 结 论
本文基于任意拉格朗日?欧拉描述法,开展了薄平板竖弯和扭转强迫运动绕流场CFD模拟,研究了薄平板大幅运动的气动特征和稳定性,得到下述结论:
1) 单自由度小幅运动的薄平板,其气动力系统是线性的,也是气动稳定的。
2) 单自由度大幅竖弯运动薄平板是气动稳定的,且气动力系统非线性不明显;但单自由度大幅扭转运动薄平板气动力系统是非线性的,其非线性随折减风速提高而显著,且折减风速较高后,其气动力系统将变得不稳定。
3) 大幅扭转的耦合运动平板,气动力系统均为非线性,其非线性主要来自扭转自由度,非线性随折减风速的提高更显著。
4) 大幅扭转的耦合运动平板气动稳定性,取决于竖弯自由度消耗的气流能量与扭转自由度吸收气流能量的相对大小。当竖弯振幅较小时和折减风速较高时,气动力系统是不稳定的;当竖弯自由度方向振幅较大时,其气动力系统将是稳定的。
參考文献:
[1] Zhu Q, Xu Y L, Zhu L D, et al. Vortex-induced vibration analysis of long-span bridges with twin-box decks under non-uniformly distributed turbulent winds[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2018,172: 31-41.
[2] Malík Josef. Sudden lateral asymmetry and torsional oscillations in the riginal Tacoma suspension bridge[J]. Journal of Sound and Vibration, 2013,332(15):3772-3789.
[3] 祝志文.超临界雷诺数下拉索顺风向自激力特性研究[J].振动工程学报,2014, 27(3):377-384.
Zhu Zhiwen. Characteristics of along wind self-excited forces of a cable under super-critical Reynolds number[J]. Journal of Vibration Engineering, 2014, 27(3):377-384.
[4] 祝志文,陈 魏,李健朋,等.多塔斜拉桥加劲索涡激振动实测与时域解析模态分解研究[J].中国公路学报,2019,32(10):247-256.
Zhu Zhiwen. CHEN Wei, LI Jianpeng,et al. Field observation of vortex-induced vibration of stiffening cables in a multi-tower cable-stayed bridge with application of analytical mode decomposition[J]. China Journal of Highway and Transport, 2019,32(10):247-256.
[5] Wu T, Kareem A. A nonlinear analysis framework for bluff-body aerodynamics: A Volterra representation of the solution of Navier-Stokes equations[J]. Journal of Fluids and Structures, 2015,54:479-502.
[6] 祝志文,石亚光,李健朋.扁平箱梁基于Volterra理论的气动力非线性特性研究[J].中国公路学报,2018, 31 (1): 74-81.
Zhu Zhiwen, Shi Yaguang, Li Jianpeng. Research on nonlinear aerodynamics of flat steel box girder based on Volterra theory[J]. China Journal of Highway and Transport , 2018, 31 (1): 74-81.
[7] 祝志文,顾 明,陈政清.两自由度系统气弹响应特性研究[J].工程力学,2008,25(8):23-30.
Zhu Zhiwen, Gu Ming, Chen Zhengqing. Study on response characteristics of two-DOF aeroelastic system[J]. Engineering Mechanics, 2008, 25(8):23-30.
[8] Filipovic Nenad, Mijailovic Srboljub, Tsuda Akira, et al. An implicit algorithm within the arbitrary Lagrangian-Eulerian formulation for solving incompressible fluid flow with large boundary oscillations[J]. Computer Methods in Applied Mechanics and Engineering, 2006,195(44-47): 6347-6361.
[9] Zhu Zhiwen, Chen Zhengqing, Gu Ming. CFD based simulations of flutter characteristics of ideal thin plates with and without central slot[J]. Wind and Structures, 2009, 12(1): 1-19.
[10] Tau E Y. A second-order Projection method for incompressible Navier-Stokes equations in arbitrary domains[J]. Journal of Computational Physics, 1994, 115:147-152.
[11] 祝志文,陳政清.数值模拟桥梁断面的颤振导数和颤振临界风速[J].中国公路学报,2004,15(4):41-50.
Zhu Zhiwen, Chen Zhengqing. Numerical simulations for aerodynamic derivatives and critical flutter velocity of bridge deck[J]. China Journal of Highway and Transport, 2004, 15(4):41-50.
[12] 祝志文,顾 明,陈政清.基于3211多阶跃激励CFD模型的颤振导数识别研究[J].振动工程学报,2008, 21(1):18-23.
Zhu Zhiwen, Gu Ming, Chen Zhengqing. Identification of flutter derivatives based on 3211 multi-step excitation of CFD model[J]. Journal of Vibration Engineering, 2008,21(1):18-23.
[13] Scanlan R H, Tomko J J. Airfoil and bridge deck flutter derivatives[J]. Journal of Engineering Mechanics, ASCE, 1971,97(6): 1171-1737.
CFD investigation on aerodynamics and stability of a two degree-of-freedom thin plate undergoing large-amplitude oscillation
ZHU Zhi-wen1, YAN Shuang1, WANG Qin-hua1, LI Jia-wu2
(1. Key Laboratory of Structure and Wind Tunnel of Guangdong Higher Education Institutes (Shantou University),
Shantou 515063, China; 2. Highway School, Chang'an University, Xi'an 710064, China)
Abstract: In order to investigate the aerodynamic characteristics and aerodynamic stability of the two degree-of-freedom (2-DOF) thin plate undergoing large-amplitude oscillation, the governing equations for arbitrary-deformed fluid domain in the two-dimensional incompressible form are numerical solved based on the Arbitrary-Lagrangian-Eulerian description and the finite difference method in moving-grid system. Then, computational fluid dynamics (CFD) is employed to simulate the flow field around the thin plate undergoing heave and/or pitch oscillation at various reduced wind speeds. The research finds that the aerodynamic system around the thin plate is linear and stability when the thin plate experiences small-amplitude vibration in heave or pitch, and it is also linear and stable even when the thin plate undergoes large-amplitude heave motion. However, when the thin plate undergoes large-amplitude pitch motion, the aerodynamic system of the thin plate presents nonlinearity which will become significant and even turn into instability with the increase of reduced wind speed. Meanwhile, when the thin plate experiences 2-DOF oscillation with large amplitude in pitch coupled with different amplitude in heave, nonlinearity will also be presented and be more significant with the increase of reduced wind speed. It is noted that such nonlinearity is generated from the large-amplitude oscillation in pitch. For the coupled vibration system with 2-DOF, when the vibration amplitude is small while the reduced wind speed is high, its aerodynamic system is instable. While when the vibration amplitude in heave is large, the aeroelastic system will be stable.
Key words: aerodynamics stability; thin plate; large-amplitude oscillation; CFD; aerodynamic nonlinearity
作者简介: 祝志文(1968-),男,教授,博士生导师。电话: 13574876655; E-mail: zhuzw@shu.edu.cn

