融合注意力LSTM的神经张量分解推荐模型
李晶晶,夏鸿斌,2,刘 渊,2
(1. 江南大学 人工智能与计算机学院,江苏 无锡 214122;2. 江苏省媒体设计与软件技术重点实验室,江苏 无锡 214122)
0 引言
近年来,随着信息网络的迅猛发展,时刻都会产生纷繁冗余的数据。用户面对海量数据很难获取有价值的信息,并且用户偏好以及用户与项目之间的关系会随着时间的推移而产生变化,因此,推荐系统成为帮助用户获取有效信息的必要工具。传统的推荐系统包括: 基于内容的推荐 (content-based recommendation)[3],利用用户历史数据进行推荐,其可扩展性和有效性非常有限;协同过滤推荐 (collaborative filtering recommendation)[1-2],利用用户与项目之间的交互信息为用户进行推荐,容易遭受数据稀疏问题;混合推荐 (hybrid recommendation)[4-5],将前两种方法进行组合。
随着深度学习技术的出现,人们为开发基于神经网络的矩阵分解模型做出了巨大努力。在非常稀疏、失衡的数据集上,Mnih等[6]提出的概率矩阵分解模型展现了其强大的解决数据稀疏问题的功能。随着数据获取能力的不断提升,如何融合用户和项目在不同领域的信息受到研究者们广泛关注。He等[7]旨在通过对用户和项目的潜在特征进行建模来开发神经网络关系数据建模框架。Shan等[8]使用MLP直接学习特征之间的交互。Chen等[9]将张量分解和对抗学习相结合以提供上下文感知的建议。随着注意力机制在自然语言理解领域取得突破性进展,Zhou等[10]提出基于注意力的双向长期短期记忆网络来捕获句子中最重要的语义信息。Liu等[11]在推荐系统中使用注意力机制捕捉用户当前兴趣和长时兴趣。
越来越多的研究凭借深度学习强大的从样本中学习数据集本质特征的能力来获取深层次的特征。Wu等[12]通过LSTM模型根据历史评分推断用户和项目的动态嵌入向量。Liu等[13]和罗等[14]将传统矩阵分解和深度学习模型相结合。后者在前者工作的基础上使用注意力机制的长短期记忆网络替换了卷积神经网络,虽然效果得到了提升,但是矩阵分解由于向量间的内积,假设潜在因子之间存在多线性交互作用,线性模型参数的较小随机扰动可能会导致较大的后向误差,缺少对潜在因子之间的非线性进行建模的能力。
上述方法的局限性在于它们仅考虑静态数据,而不考虑需要探索时间维度的动态数据[15],缺乏学习不同潜在因子之间的非线性交互能力。Wu等[16]将三向张量(即用户、项目、时间)作为输入,并学习张量每个维度的潜在嵌入,使用长短期记忆网络于动态时间因子特征提取,展现了优异的性能。但是,考虑到与无用特征的交互可能会引入噪声并降低性能,我们在Wu等模型[16]的基础上,结合时间交互学习与基于注意力机制的长短期记忆网络(LSTM-attention)来构建推荐模型(LSTM-attention NTF,LA-NTF)。依次获取用户、项目和时间的潜在向量,然后将用户、项目和时间的潜在向量集成到多层感知器中来预测用户评分。通过神经网络强大的特征提取能力,进一步解决数据稀疏问题。
综上所述,本文主要贡献包括:
(1) 使用基于注意力机制的LSTM来增强特征提取能力,突出项目文本关键信息。
(2) 对时间动态建模后增加注意力层,进一步提取时间因子特征。
1 融合注意力LSTM的神经张量分解推荐模型
1.1 LA-NTF模型
LA-NTF是一种多层表示学习模型,对张量分解进行全神经处理来明确地建模不同维度之间的时间动态变化。融合时间交互学习和注意力长短期记忆网络的张量分解推荐模型结构如图1所示。该模型分为四个部分。

图1 LA-NTF模型
(1)用户嵌入层Ui: 输入用户名称和评分数据,输出用户的潜在向量。
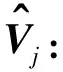


1.1.1 张量分解
张量分解(tensor factorization,TF)的关键思想是学习张量中观测值之间的联系以推断缺失值。TF将张量χ分解为三个不同的矩阵,U∈RI×L,V∈RJ×L和T∈RK×L,其中L是潜在因子的数目(以l为索引),将张量χ定义为式(1):

(1)
其中,U:,l,V:,l和T:,l分别代表矩阵U,V和T的第l列,∘表示向量的外积。每个xi,j,k∈χ可以由三个L维向量的内积计算如式(2)所示。
(2)
张量分解的目的是学习U,V和T的最大似然估计,进一步定义Ui,Vj和Tk,分别来索引U∈RI×L,V∈RJ×L和T∈RK×L的行,模型从观察到的张量χ中获知U,V和T之后,根据式(2)计算张量χ的缺失数据值。
1.1.2 LSTM网络结构
LSTM是一种特殊的循环神经网络结构,用于长期依赖关系的建模,并通过开发更复杂的隐藏单元来解决梯度消失问题。LSTM具有在时间序列上强大的记忆能力和对文本的表征建模能力,并且能够学习较长序列文本依赖而不局限于局部特征之中。LSTM的组成结构是: 输入门,输出门,遗忘门和一个记忆单元。
t时刻输入状态为xt,上一时刻LSTM的输出状态为ht-1。具体计算过程如式(3)~式(8)所示。
1.1.3 项目建模
在LSTM层提取项目潜在向量后引入注意力层。注意力机制能够赋予文本不同的关注度,从众多信息中选择关注关键信息。模型结构如图2所示。

图2 LSTM-attention结构图

(9)
Attention层:引用了关系分类任务的注意力机制[10]来捕捉句子中最重要的语义信息,通过权向量的乘法,将每个时间步长的词级特征合并为一个句子集特征向量,如式(10)~式(12)所示。
H是由LSTM层的输出向量[h′0,h′1,…,h′s-1]组成的矩阵,其中H∈Rdw×T,dw是词向量的维度,w是训练参数向量,wT是转置。γ表示特征向量,由上下文向量与单词特征向量加权求和得出。

(13)
其中,W′T∈Rw×L是投影矩阵,b′T∈RL是投影偏置。
1.1.4 时间动态建模
在LSTM层提取时间潜在向量后引入注意力层,注意力机制能够自适应地结合文本上下文信息,提高模型分类准确度。模型结构如图3所示。
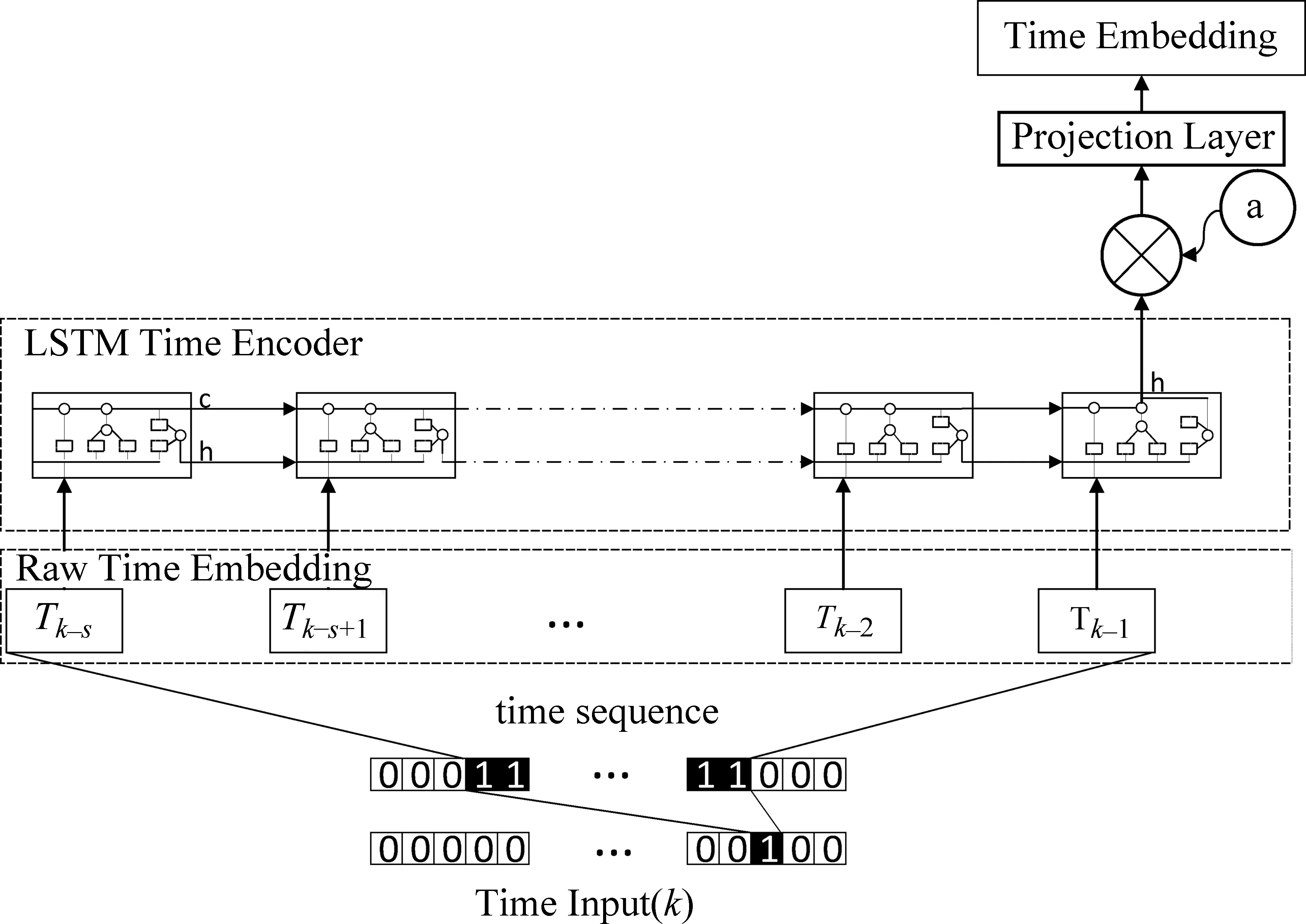
图3 LSTM-attention结构图
假设当前时隙的嵌入向量取决于先前时隙中的嵌入向量,在LA-NTF中,我们基于过去s时隙中的嵌入向量来预测当前时隙中的嵌入向量,LSTM层生成时间嵌入向量以对不断变化的时间隐藏因子进行编码。在时间序列编码为以下形式时,将隐藏状态ct和ht定义为式(14):
(14)
Attention层: LSTM层提取时间潜在向量后引入注意力层,从众多时间因子信息中捕捉重要时间因子的特征信息,如式(15)~式(17)所示。
其中,Ww是权重系数,bw为偏置系数,uw为随机初始化的attention矩阵,τ表示特征向量。

(18)
其中,WT∈Rs×L是投影矩阵,bT∈RL是投影偏置。
1.1.5 多层感知器


(19)
其中,n表示由l索引的隐藏层数,“;”表示连接操作,对于Zl层,φl,Wl和bl分别表示MLP的激活函数(ReLU,sigmoid,tanh)、权重矩阵和偏置。
1.2 LA-NTF模型优化过程
1.2.1 目标函数

(20)
其中,X表示张量χ中观察到的交互数据的集合。LA-NTF通过最小化观察到的交互数据和因式分解来表示上述损失函数。
1.2.2 批量归一化
在神经网络模型的训练过程中,其性能可能会因为协方差偏移而降低。为解决这一问题,采用了批量归一化(batch normalization,BN)[18],可以在将上一层的输入数据作为输入发送到下一层之前对其进行规范化处理[19]。在LA-NTF框架中,将BN应用于每次小批量训练中,通过将输入转换为零均值/单位方差分布来减少内部协方差偏移。BN应用于LSTM层以避免训练过程中的减速,如式(21)所示。

(21)
其中,BN(·)代表批量归一化操作。
1.2.3 学习算法


算法: LA-NTF输入: 张量χ∈RI×J×K,交互集合X,时间序列的大小s,训练批量bsize参数: 用户嵌入矩阵U∈RI×L,项目嵌入矩阵V∈RJ×L,时间嵌入矩阵T∈RK×L,以及其他隐藏参数θStep1:初始化所有参数//取样大小为bsize的小批量Step2:for eachTbatch=样本(X,bsize)doStep3: for each〈i,j,k〉∈Tbatchdo /∗集合所有维度的嵌入∗/Step4: Ui=U[i,: ];Step5: x=x0,h′=h′0,c=c0,h=h0; //初始化所有隐藏状态Step6: for 0至(s-1) do

续表
2 实验
本文的实验环境设置为: Windows 10基于x64的处理器,Pycharm 2018,Inter(R) Core(TM) i7-8700k CPU @ 3.70GHz,16 GB内存,Python 3.7。选择使用的深度学习框架为Tensorflow,并选择Adam作为优化器来学习模型参数。
2.1 实验数据集
Netflix和MovieLens-1M公开数据集被广泛应用在电影评分预测中。数据集中用户评定的分数与评级日期相关联,以表示何时进行评级。Netflix包含68 079位用户对2 328部电影的1 000万多条评级数据,收集时间为2002年1月至2005年12月。MovieLens-1M包含6 040位用户对3 900部电影的100万多条评级数据,收集时间为2000年4月至2003年2月。我们通过将每部电影与收集时间内对这部电影进行评级的用户相关联,生成张量χ。
2.2 实验评价指标
为了评估比较算法在评分预测时的性能,采用均方根误差(RMSE)和平均绝对误差(MAE)作为评价指标,如式(22)、式(23)所示。

2.3 基线模型
为了验证提出的LA-NTF模型的性能,对比实验如下:
(1)PMF: Mnih等[6]提出矩阵分解的一种概率方法,它为每个用户和每个项目分配一个遵循高斯分布的潜在特征向量,评级从相应潜在特征的内积得出。
(2)RRN: Wu等[12]为用户和项目指定两个嵌入向量来预测用户和项目之间的未来交互。
(3)PHD: Liu等[13]使用aSDAE提取用户潜在向量,同时使用CNN提取项目潜在向量,最终集成到PMF框架中来预测评级。
(4)NCF: He等[7]提出一个基于神经网络的协同过滤的通用框架,来模拟用户和项目的潜在特征。
(5)NTF: Wu等[16]提出一种基于神经网络的张量分解,其中LSTM表征关系数据的多维时间交互。
(6)A-NTF: 在LSTM对时间动态数据建模中加入注意力机制的NTF模型。
(7)LA-NTF: 在模型(6)中增加使用基于注意力机制的LSTM增强项目特征提取能力的模型。
2.4 实验结果及分析
2.4.1 实验参数设置
几种对比实验方法参数设置如表1所示。

表1 模型参数设置
2.4.2 实验分析
(1) 讨论在相同实验环境下不同基线方法的性能表现。
本实验将数据集分别按3∶1∶6、5∶1∶4、7∶1∶2的比例划分为训练集、验证集和测试集。改变训练集比例在两个不同稀疏度的数据集上的预测性能,结果如表2、表3所示。

表2 MovieLens-1M数据集上不同模型的性能比较

表3 Netflix数据集上不同模型的性能比较
从表2和表3可以看出,LA-NTF模型在两个数据集上的RMSE和MAE表现均优于其他模型。随着训练量的减少,LA-NTF与其他算法之间的性能增益变大。说明张量分解有效地填补了稀疏张量中缺失的数据,并挖掘出了数据之间的潜在关系,同时也验证了LA-NTF模型预测稀疏张量相互作用的能力。在MovieLens-1M数据集中,训练数据为30%和50%时性能有显著提升,在训练数据为70%的情况下,LA-NTF(ReLU)模型比PMF、RRN、PHD、NCF、NTF(ReLU)模型RMSE分别提高了23.06%、11.27%、3.90%、4.05%、1.84%,MAE分别提高了15.13%、9.06%、3.40%、3.61%、1.57%。这说明在NTF的框架下使用LSTM和引入注意力机制,有效提高了模型性能。从Netflix数据集中看出,训练数据为30%和50%时性能有明显提升,在训练数据为70%的情况下,LA-NTF(ReLU)模型比PMF、RRN、PHD、NCF、NTF(ReLU)模型RMSE分别提高了2.24%、4.09%、4.00%、2.84%、1.49%,MAE分别提高了1.26%、3.63%、3.88%、2.40%、1.32%,这说明LA-NTF在捕获多维关系数据中的非线性交互作用方面的有效性,以及MLP激活函数的选择对模型性能影响不大。
使用不同大小的训练数据集,LA-NTF可以得到明显的改进,证明LA-NTF对于数据稀疏性问题是可靠的。随着训练量的增加,可以观察到性能呈上升趋势,这表明训练数据量对预测评分的积极作用。与传统的矩阵分解算法(PMF)相比,基于神经网络的模型(即RRN、PHD和NCF)在训练数据较少的情况下具有更好的性能。这表明基于神经网络的模型更适合于稀疏关系数据。
A-NTF和LA-NTF模型的RMSE和MAE性能都优于NTF模型,说明注意力机制为每个时间因子分配相应的权重,可以有效地从众多时间因子信息中捕捉重要时间因子的特征信息,从而提高模型精度。
(2) 讨论训练批量大小的不同的情况下不同基线方法的RMSE和MAE评估标准的表现。
本实验将数据集按5∶1∶4的比例划分为训练集、验证集和测试集,MLP以ReLU作为激活函数。在两个不同稀疏度的数据集上进行实验,结果如图4所示。


图4 训练批量对RMSE和MAE的影响
从图4可以看出,在两个数据集上随着训练批量值的增加,几个算法都呈稳定的趋势,但在较稀疏的MovieLens-1M上传统方法PMF模型效果最差。这是因为PMF模型忽略了用户与项目之间交互信息的作用,使得推荐结果不佳。PHD模型优于PMF模型,这说明结合深度学习模型和传统的矩阵分解方法可以更好地提取重要信息,学习更有效的潜在因子。而LA-NTF模型和A-NTF模型都明显优于NTF模型,这说明注意力机制能够赋予每个时间因子不同的关注度,有效地从众多时间因子信息中捕捉重要时间因子的特征信息。在较密集的Netflix数据集上PMF模型性能要优于PHD模型,说明基于神经网络的模型更适合处理稀疏关系数据。RRN和NCF对关系数据进行静态或顺序建模的假设受到限制,没有考虑到关系数据随时间变化的潜在因子的变化,从而导致推荐效果不理想。从两个数据集可以看出,LA-NTF模型优于A-NTF模型,因为使用注意力机制的LSTM对项目文本信息进行表征建模,有效地从众多文本信息中突出关键文本的信息,从而提高了模型的推荐性能。
(3) 讨论嵌入层的大小、时间步长以及MLP隐藏层数的设置如何影响模型的性能?
本实验将Netflix数据集按5∶1∶4的比例划分为训练集、验证集和测试集,MLP以ReLU作为激活函数,结果如图5~图7所示。
NTF、A-NTF和LA-NTF模型对于参数选择不敏感,除了隐藏层数之外,可以通过具有成本效益的参数实现高性能,即参数越小,训练过程就越有效。从图5、图6可以观察到嵌入层大小与时间步长对模型性能的影响呈正相关,参数的大小对RMSE和MAE值影响不大。图7表明只要隐藏层数大于2,模型的性能就几乎稳定。在设置不同参数的情况下,LA-NTF较A-NTF模型性能更好,这说明LSTM能建立单词之间的长期依赖而不局限于局部特征,注意力机制能自适应地结合上下文中

图5 嵌入层大小对模型RMSE和MAE的影响

图6 时间步长对模型RMSE和MAE的影响

图7 隐藏层数对模型RMSE和MAE的影响
的关键语义信息,提高模型分类准确度,从而提高推荐性能。A-NTF和LA-NTF模型较NTF模型在隐藏层数为1时收敛更快,说明注意力机制能快速突出关键信息,提取时间因子深层次特征并能快速收敛,使推荐性能更优。
3 结束语
由于传统推荐方法对关系数据进行静态或顺序建模的假设受到限制,缺乏考虑随着时间的推移用户偏好以及推动用户与项目之间的关系随时间变化的潜在因子的变化。为解决不断发展的用户和项目间关系数据的挑战,使用长短期记忆网络和注意力机制进一步捕捉多维度时间序列下用户项目之间的交互作用。在MovieLens-1M和Netflix数据集的评分预测任务上,LA-NTF模型的表现优于基线模型,这说明本文提出的LA-NTF模型通过对动态关系数据进行建模,充分学习不同潜在因子之间的非线性交互作用对推荐性能有益。

