基于SVS-603传感器的波浪反演技术及海上比测数据分析

王志，周扬*，杨俊贤，郑威，赵彬，于雨，蔡志文

(1.齐鲁工业大学(山东省科学院) 山东省科学院海洋仪器仪表研究所 山东省海洋环境监测技术重点实验室 国家海洋监测设备工程技术研究中心，山东 青岛 266061；2.南方海洋科学与工程广东省实验室(湛江)，广东 湛江 524000；3. 中国船舶科学研究中心，江苏 无锡 214002)

波浪实测装备是了解海洋、研究海洋的重要物质基础，其中基于加速度传感器的波浪测量装备是最为常用的。国外基于加速度传感器的波浪浮标研究起步比较早，目前较为成熟的产品包括Datawell公司的Waverider系列浮标，加拿大AXYS公司的TRIAXTS系列浮标等[1]。国内也有一些自主研发的浮标，其中具有代表性的是山东省科学院海洋仪器仪表研究所的SBF系列浮标[2]和中国海洋大学研发的SZF浮标[3]，但是跟国外成熟产品相比还有一定的差距。近年来，很多大学和研究机构都开展了波浪浮标的研发工作，但都没有形成具有竞争优势的产品。

基于加速度传感器的波浪浮标，其主要原理是通过加速度传感器测得三向加速度，通过二次积分得到三向位移，之后对三向位移进行傅里叶变换就可以得到波浪谱[4]。但在实际研发中，却存在非常多的问题。首先，要保证浮标体的随波性，即所测得的加速度必须与水质点加速度足够接近，否则无法提供有效的实测加速度；其次，如何由加速度积分变为位移是一个非常重要的问题，其中涉及滤波、数值积分等问题；最后，波浪谱的计算方法、滤波窗的选择也会影响最终的结果。

SVS-603加速度传感器是美国SeaView System公司研发的一款基于九轴惯性测量单元的波浪传感器，可提供原始的加速度实测值；Datawell公司研发的DWR-MKIII浮标则能提供三向位移。本文将对这两款设备性能进行对比，进而研究其特性，这对于波浪测量装备的自主研发具有借鉴意义。

1 试验设备和过程

SVS-603波浪传感器配套的软件可以对实测数据进行简单的数据分析，获得波浪参数(有义波高、谱峰周期、谱峰浪向等)、能量谱和方向谱，同时还给出了三向加速度及三向位移对应的傅里叶系数，一些性能参数见表1，更具体的信息可参见其说明书[5]。SVS-603已经有一些实用案例，如英国的Planet Ocean使用了该款传感器。

2020年4月8日在青岛某码头进行了SVS-603波浪传感器和DWR-MKIII浮标实测数据的对比试验，当天海况等级二级，适合出海作业，设备布放地点水深10 m，采用单点系泊的方式将DWR-MKIII锚定在指定地点，获取了2020年4月8日9：21—13：00的试验数据。

DWR-MKIII是一款非常成熟的基于加速度的波浪浮标，研究者将其与浪高仪阵列做了大量对比[6-7]，一些简要的性能参数见表1。

表1 SVS-603和DWR-MKIII的性能参数

本次试验的方法是将SVS-603传感器安装到DWR-MKIII的浮标体内，目的是保证两个加速度传感器的位置相对固定，使两个传感器保持一致的随波性。由于DWR-MKIII标体的内部结构限制，最终SVS-603在浮标体内的相对安装位置如图1所示。

图1 SVS-603传感器安装位置示意图Fig.1 The installation position diagram of SVS-603 sensor

2 波浪反演算法

波浪反演算法是波浪数据处理最重要的部分，下面给出SVS-603的加速度-位移传递函数。

对加速度进行两次积分可以得到位移：

s(t)=∬a(t)dt+s0+kt，

(1)

其中a(t)是加速度，s(t)是位移，s0和kt是趋势项，通过多项式拟合可以去除趋势项。然而在实际设备中，无法直接通过该手段计算位移，这是因为测量信号本身有误差，两次积分后误差会增大。还有一个更重要的原因是低频信号会严重影响积分结果。

通常的做法是使用频域积分方法：

s(t)=F-1{H(ω)F[a(t)]}，

(2)

其中F和F-1分别是傅里叶变换及其逆变换，ω是圆频率，H(ω)是传递函数：

(3)

其中G(ω)是滤波函数，最简单的一种滤波函数是：

(4)

其中ω0是截断频率。此外还有一些其他常用的滤波函数，如Hong等[8]等提出的滤波函数，更早的一些方法见Gavin等[9]的综述。

图2～4给出了SVS-603三个方向的传递函数。可以看到，水平方向的传递函数非常接近式(4)，其截断频率是T=10.24 s，即ω0=0.614 rad/s。垂向传递函数则更为复杂，不同系列的截断频率各不相同，而且即使频率大于截断频率的个别传递函数依旧等于0。

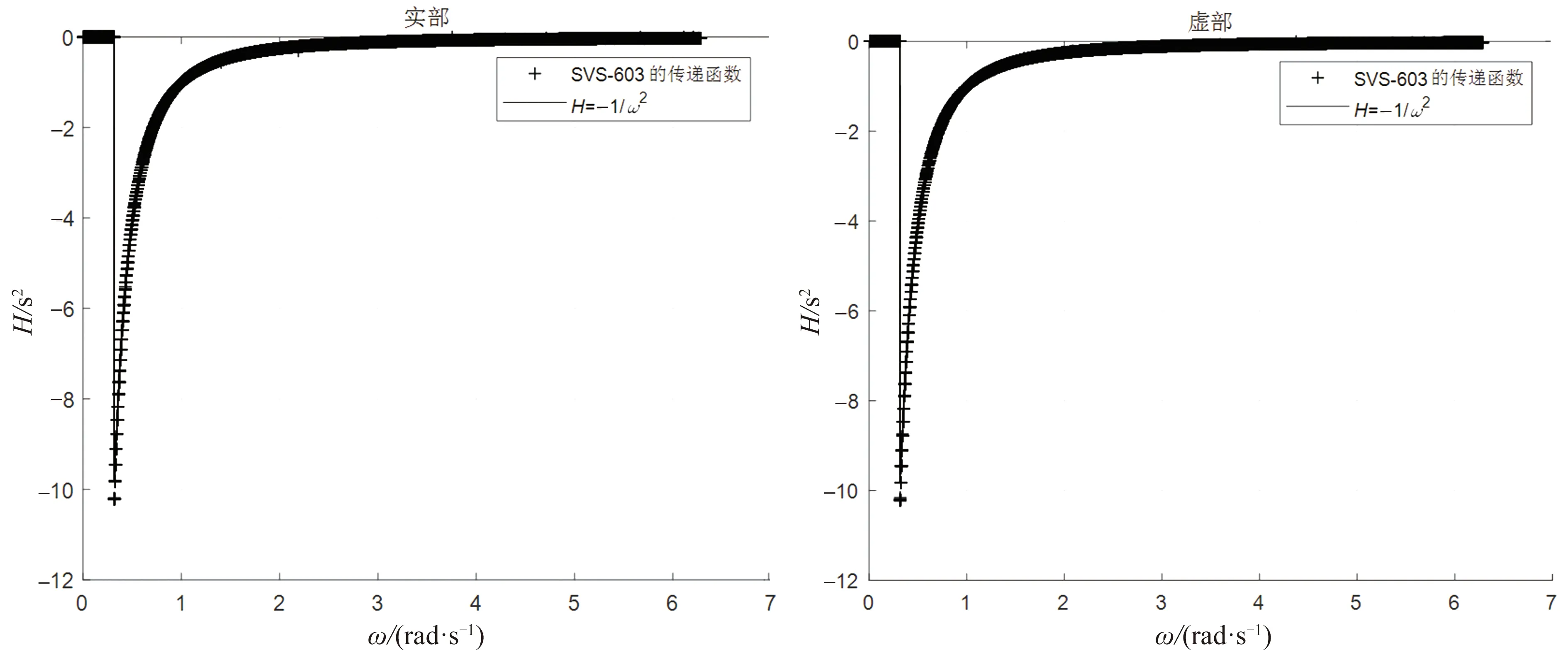
图2 SVS-603北向加速度-位移传递函数Fig.2 Transfer function of north acceleration-displacement for SVS-603

图3 SVS-603东向加速度-位移传递函数Fig.3 Transfer function of east acceleration-displacement for SVS-603

图4 SVS-603垂向加速度-位移传递函数Fig.4 Transfer function of vertical acceleration-displacement for SVS-603

假定波浪振幅很小且由大量振幅不同、相位不同的波浪迭加而成，可推导出任意两个波浪特性间的互谱等于相应波浪特性与波面传递函数乘积的傅里叶变换，即

(5)

其中：f代表海浪频率；k代表波数；φmn(f)代表第m个测点上和第n个测点波浪特性之间的互谱；Hm是测点m对应的传递函数；S(f,θ)代表海浪方向谱；xmn、ymn分别代表m和n测点之间的距离在x和y轴向上的投影距离。常用的方向谱估计算法有最大似然算法、贝叶斯算法、最大熵算法、傅里叶算法等，其中最常用的是最大似然算法，该算法的方向谱估计值为：

(6)

主浪向为在二维方向谱中所有最大值对应的方向，峰值浪向为在一维高度谱最大值点对应的波浪方向。

3 实测数据分析

3.1 SVS-603传感器的位移和DWR-MKIII位移对比

将SVS-603给出位移的傅里叶系数进行傅里叶逆变换，并与DWR-MKIII的位移进行比较，研究两者基础数据的差别。

图5给出了三向位移的对比情况。SVS-603和DWR-MKIII所给出的北向位移在趋势上有一定吻合的地方，比如在12：45之后两者都增大，而东向位移则两者完全没有一致性。SVS-603所给出的东西位移时而大时而小，其原因与上文所述的SVS-603不在浮标体正中心有关。垂向位移则两者趋势几乎一样。但注意到SVS-603由傅里叶系数换算得到的垂向位移整体要比DWR-MKIII小一些，这与图2不符。图6给出了由位移计算出的有义波高和SVS-603自身给出的有义波高对比，可以看到两者线性关系很好，但其比值并不是1，这是由于其算法导致的误差。

图5 SVS-603与DWR-MKIII三向位移对比Fig.5 Three-way displacement comparison between SVS-603 andDWR-MKIII

图6 位移算出的和SVS-603给出的有义波高对比Fig.6 The significant wave height comparison between calculatedby displacement and given by DWR-MKII

3.2 波浪谱的对比分析

SVS-603和DWR-MKIII都可以给出能谱和方向谱，但如前文所述，由于SVS-603的浪向与DWR-MKIII存在一定的差异，因此这里进行能谱对比。其中，SVS-603的波浪谱由垂向位移的傅里叶系数得到：

(7)

其中，C(f)是垂向位移的傅里叶系数。因为SVS-603是每隔17 min测一次，所以本文提取接近半点的波浪谱与DWR-MKIII进行对比。

图7对比了DWR-MKIII和SVS-603的能谱。基本上两者是比较相似的。但也注意到在某些时刻，比如10:00和12:00，SVS-603自身的低通滤波器并没有完全地将低频信号过滤掉，这影响到波浪谱，进而影响谱峰周期等参数，见图7。因此使用SVS-603时，需要特别注意这一点，图7表明对谱进行时域光顺后，得到的谱峰周期和DWR-MKIII比较接近。但这一结论是否能推广到所有波浪值需进一步研究。实际上，DWR-MKIII的波浪谱所采用的光顺方法反而更接近频域光顺，其窗函数的宽度大约是自相关函数小于2倍标准差时所在的位置，这一方法值得借鉴。

图7 SVS-603与DWR-MKIII的波浪谱对比Fig.7 Comparison of wave spectrum between SVS-603 and DWR-MKIII

3.3 波浪特征值比测分析

图8 ～11对比了SVS-603给出的谱峰周期、有义波高、平均跨零周期和谱峰浪向随时间的变化，并与DWR-MKIII进行对比。

图8 SVS-603和DWR-MKIII谱峰周期对比Fig.8 Peak spectral period comparison of SVS-603 and DWR-MKIII

从图9看到SVS-603和DWR-MKIII的有义波高非常接近，绝对误差在0.1 m左右。注意到11:30之后，SVS-603的有义波高有一定振荡。同样的结论也适合于平均跨零周期，在11:30之前，两者非常接近，绝对误差在0.2 s以内，但11:30之后SVS-603的周期出现振荡。

图9 SVS-603和DWR-MKIII有义波高对比Fig.9 Significant wave height comparison of SVS-603 and DWR-MKIII

图10 SVS-603和DWR-MKIII平均跨零周期对比 Fig.10 Average zero crossing period comparison of SVS-603 and DWR-MKIII

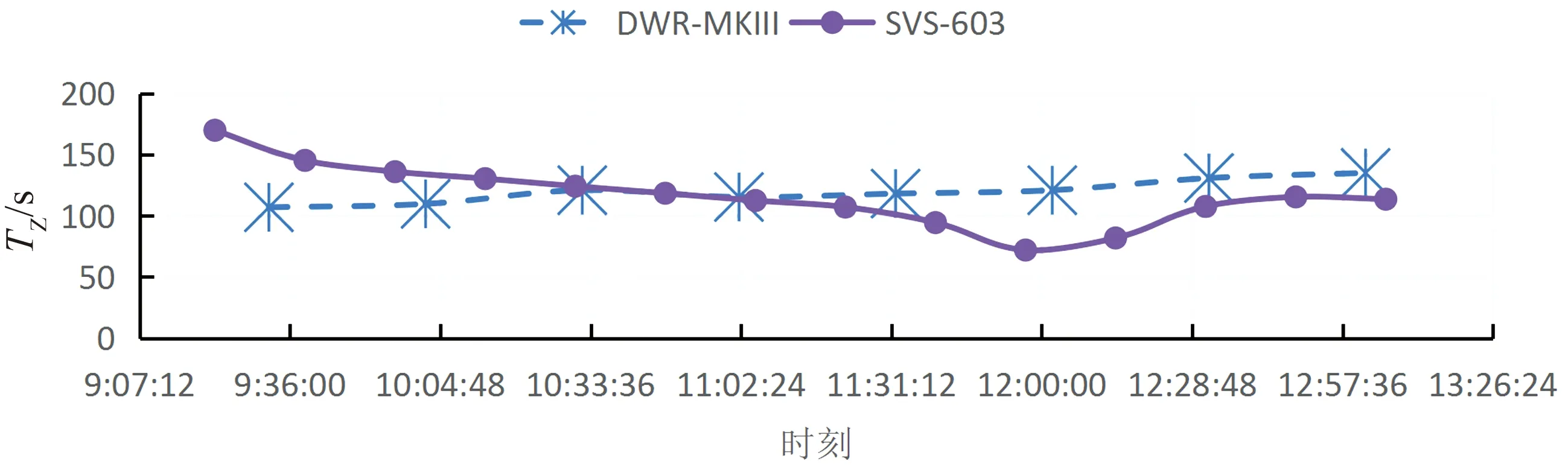
图11 SVS-603和DWR-MKIII谱峰浪向对比Fig.11 Spectral peak wave direction comparison of SVS-603 and DWR-MKIII

和有义波高及平均周期不一样，谱峰周期往往受谱光顺算法的影响。SVS-603提供3种谱峰周期，分别是原始谱峰周期(未光顺)、经过频域光顺的谱峰周期(频域光顺)和经过时域光顺的谱峰周期(时域光顺)。从图8中看到，时域光顺的谱峰周期与DWR-MKIII给出的谱峰周期最为接近。而未经过光顺和经过频域光顺的谱峰周期则偶尔会受低频信号的影响。

SVS-603所得的谱峰浪向(时域光顺)与DWR-MKIII的谱峰浪向有比较大的差别。DWR-MKIII测得的谱峰浪向从100°逐渐往南转，最后落在135°；而SVS-603则完全相反，从南向(170°)逐渐往北变化，而且在11:56和12:14发生振荡，振荡位置与波高和周期振荡时间一致，而振荡的原因可以从图8得到。如前文所述，在该时刻SVS-603自身的低通滤波器并没有完全地将低频信号过滤掉，这影响到谱，进而影响谱峰周期等参数。关于浪向不一致的原因，初步分析是SVS-603没有被放置在浮标的正中心，导致水平方向加速度有所偏差。

4 结论

本文基于SVS-603传感器进行波浪反演技术分析，并利用该传感器与DWR-MKIII进行海上对比试验，得到以下结论：

(1)SVS-603和DWR-MKIII测得的有义波高和平均跨零周期非常接近；

(2)SVS-603的谱峰周期受光顺算法影响，其中时域光顺算法得到的谱峰周期与DWR-MKIII最为接近；

(3)对SVS-603的加速度谱和位移谱研究发现，其水平方向的传递函数接近一个简单的截断函数，截断频率为1/10.24 Hz，而垂向的传递函数则比较复杂；

(4)对比SVS-603和DWR-MKIII的能谱发现，部分SVS-603的原始能谱受低频信号影响较大，在实际使用中需要进一步处理。

通过对两个加速度原理波浪传感器的实测数据进行分析，进而改进现有波浪算法，能够为加速度原理波浪设备研发提供更加准确的波浪算法，对我国波浪测量装备的国产化研究具有重要意义。