极化码四阶核矩阵的构造
马奎明,李秀丽
(青岛科技大学 数理学院,山东 青岛 266061)
极化码是近年来备受关注的一种纠错码,是通过信道极化(channel polarization),在编码侧使子信道呈现出不同的可靠性,当码长N持续增长时,部分信道将趋向于容量近于1的完美信道,另一部分信道趋向于容量接近于0的纯噪信道的新型编码方式。
极化码在理论上可用于任何具有低复杂度[1]的对称二进制离散无记忆信道,是目前唯一被严格证明能够达到信道容量的编码方式,与其他传统编码有较为明显的区别,可用于证明许多理论问题, 在无线通信中有广泛应用。
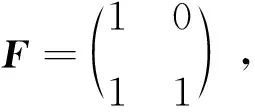

1 预备知识
记W:X→Y表示一般的二进制输入离散无记忆信道,其中X表示输入字符的集合,Y表示输出字符的集合。
定义1:如果存在一个置换π:Y→Y,对所有的y∈Y都有π(y)=π-1(y)且W(y|1)=W(π(y)|0),那么称这个二进制输入离散无记忆信道(B-DMC)W:{0,1}→Y是对称的。如果对任意y∈Y有W(y|0)W(y|1)=0或W(y|0)=W(y|1),那么称其为二进制删除信道(BEC)[5]。
对极化码的研究,还需要两个重要的信道参数:
对称容量:
巴氏参数:
这些参数分别被用作信道传输速率和传输可靠性的度量。I(W)是等概率情况下在信道W之间进行可靠通信的最高速率。Z(W)是信道W仅用于传输0或1时的最大似然决策下错误概率的上界。在上述公式中,均使用以2为底的对数,因此I(W)和Z(W)都取值于[0,1]。
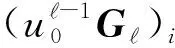

其中,i=0,1,…,-1,且令Z(i)表示巴氏参数:

定义3[3]:对任意0 E(G)也称为矩阵G的指数。 指数的定义为极化码提供了在串行相消译码策略[7]下一个有意义的性能度量。事实上,指数与信道无关。指数E(G)也可以表示为W的距离的函数。 定义4[3]给定×阶矩阵偏序距离Di(i=1,2,…,)为 其中dH(…,…)表示汉明距离; 在这一部分,主要讨论四阶核矩阵,换句话说极化码块长度为N=4n。 令W:{0,1}→Y是二进制输入离散无记忆信道,G是一个4×4阶核矩阵。给定4个二进制输入信道W(i):{0,1}→Y4×{0,1}i(i=0,1,2,3)如下: Arikan[1]的研究表明对核矩阵G会有多种选择。显然,不同的核矩阵会导致不同的性能,因此有必要寻找一种策略来设计一个适合的有限块长度的G。对于任意的核矩阵都有一些通用的策略[8],我们首先讨论如何从所有可能的核矩阵中选择一个好的。 Arikan[1]认为,矩阵G的指数越大,实现信道极化的程度越彻底,性能越好。因此,如果想找到块长度为N=4n时的最佳极化码,那么就需要找到指数最大的核矩阵。根据Arikan做的工作,当≤10时,不存在指数大于的矩阵。事实上,我们可以找到指数等于的四阶核矩阵。 证明首先考虑m=4的情况,这意味着最后一行的所有项都是1。xi是u0,u1,u2,u3的函数,因此用gi((u0,u1,u2,u3)G)[9]来表示W(yi|xi),i=0,1,2,3。那么 根据递归结构,有 这里⊕是模2的和。这个方程可以通过一个简单的例子来验证,例如N=4。 证明: 显然成立,证毕。 根据递归结构,有 如果W是BEC,等式成立。 证明:首先,给出对递归信道表达式有用的方程。 下面,使用不等式 当abcd=0或a=d或b=c时,等号成立。 =4Z(W)2-4Z(W)3+Z(W)4, +(β0δ0+β1δ1+β1δ0+β0δ1) +(β0δ0+β1δ1+β1δ0+β0δ1) =4Z(W)-2Z(W)2。 Arikan引入的核矩阵G2是唯一的,然而块长度为N=4n的极化码对G4有多种选择,因此其提供了很大的灵活性,但问题是如何找到一种策略来设计一个好的G4。当然,对齐为任意整数,且≥3所有G,都具有这样的特性。但是随着的增大,这个问题就越来越难解决了。因此我们关注最简单的情况,并提出从所有可能的G4中选择一个好的G4的策略。该策略基于的递归公式,因为这些公式直接决定了性能。然而,有些递归公式只提供了上限,而不是确切的值,如果信道W不是BEC,那么我们所做的只是一些近似的分析。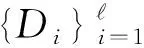
2 核矩阵的选择

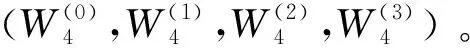
2.1 极化率
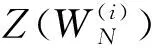
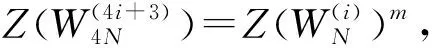
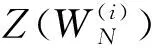





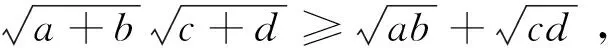

3 结语

