“点全?线联?面融”式教材解读与实践思考
张文珠
[摘 要]教材解读为教学素材与素养目标之间勾画实践路径.教师可利用“点全·线联·面融”式的解读方法对教材进行单元整体分析及知识整合,让零散的知识变得立体有层次、系统有框架,帮助学生构建完整的知识体系,综合提高学生的数学素养.
[关键词]“点全·线联·面融”;教材解读;教材素材
[中图分类号] G633.6 [文献标识码] A [文章编号] 1674-6058(2021)02-0025-02
高效的课堂教学实践取决于有效的教学设计,有效的教学设计有赖于教材的深度解读.教材解读为教学素材与素养目标之间勾画实践路径.教师可利用“点全·线联·面融”式的解读方法对教材进行单元整体分析及知识整合,让零散的知识变得立体有层次、系统有框架,帮助学生构建完整的知识体系,综合提高学生的数学素养.笔者以苏科版七年级数学下册“有理数的乘方”为例,谈谈对“点全·线联·面融”式教材解读与实践的思考.
一、教材素材
“有理数的乘方”课时的素材分为两类, 即“显性”的知识素材和“隐性”的素养素材.
在知识素材层面,学生小学阶段已学习了正数的平方、立方运算,能用于解决正方形的面积、立方体的体积等相关问题.初中阶段,学生刚学完有理数的加、减、乘、除运算,将这些已有知识进行整合、再理解,能为本课时的教学提供很好的知识素材.
在素养素材层面,学生已初步具有对数学问题进行自主探究、合作交流的意识与能力.当学生遇到现实生活中的数学问题时,他们潜意识中会应用数学的知识来解决.教师要充分利用学生这一特点,引导学生利用乘方的相关知识解决生活问题.
二、“点全·线联·面融”式教材解读
1.知识点解读——点全
乘方是有理数的一种基本运算,它是有理数乘法的推广和延续.让学生结合自己的生活经验,探求乘方的运算方法,在此基础上对幂、底数、指数的概念以及乘方的符号法则的归纳是本课的知识点.乘方是后续学习有理数的混合运算、科学记数法和开方的基础,起到承前启后、铺路架桥的作用.
2.知识线解读——线联
显性知识线:乘方的意义—乘方的概念解读—乘方的符号原则.学生对“乘方的意义”已有知识储备,比较容易接受;“乘方的概念解读”是全新知识,讲解时要透、全;“乘方的符号原则”为后续的有理数乘方的运算打下坚实的基础.
隐性思想方法线:本节课主要是在生活实践的基础上通过类比(类比正方形的面积、立方体的体积)理解乘方的意义,通过特殊到一般掌握有理数乘方的运算本质.“分类讨论”数学思想方法起着举足轻重的作用.
3.知识面解读——面融
显性知识面:“有理数的乘方”是 “有理数”这一章节的难点,同时又是整个初中阶段“数与式”中很重要的基础.例如在“代数式”“幂的运算”“实数”等章节中,“乘方”无处不在,处处渗透,足见本课时在初中数学中的重要地位.
隐性能力层面:本课时通过创设问题情境,激发学生学习数学的兴趣;通过对乘方意义的探索,培养学生观察、比较、分析、归纳及概括的能力;通过乘方运算的运用,培养学生的逻辑思维能力;通过乘方的故事以及改编,向学生展示数学与生活的紧密联系.
三、基于教材解读的教学实践
1.创设情境,导出课题
在印度有一个古老的传说,舍罕王打算奖赏国际象棋的发明人——宰相:西萨·班·达依尔.国王问他想要什么,他对国王说:“陛下,请您在这张棋盘的第1个小格里,赏给我1粒麦子,在第2个小格里给2粒,第3个小格里给4粒,以后每一小格的麦子都比前一小格多一倍.请您把棋盘上64格的麦粒都赏给您的仆人吧!”国王觉得这要求太容易满足了,就命令人们给他这些麦粒.当人们把一袋一袋麦子搬来开始计数时,国王才发现:就算把全印度甚至全世界的麦粒全拿来,也满足不了宰相的要求. 那么,宰相要求得到的麦粒到底有多少呢?
评析:将抽象的数学知识寓于故事中,拉近了数学与生活的距离.在解决问题的过程中,数据多而且庞大,学生解决问题的热情逐渐消减,但是强烈的求知欲促使他们寻求问题的答案,此时,教师导入课题,更加激发了学生的求知欲,为新课的展开做了很好的铺垫,回答了“知识从哪里来?”的问题.
2.整体构架,引出新知
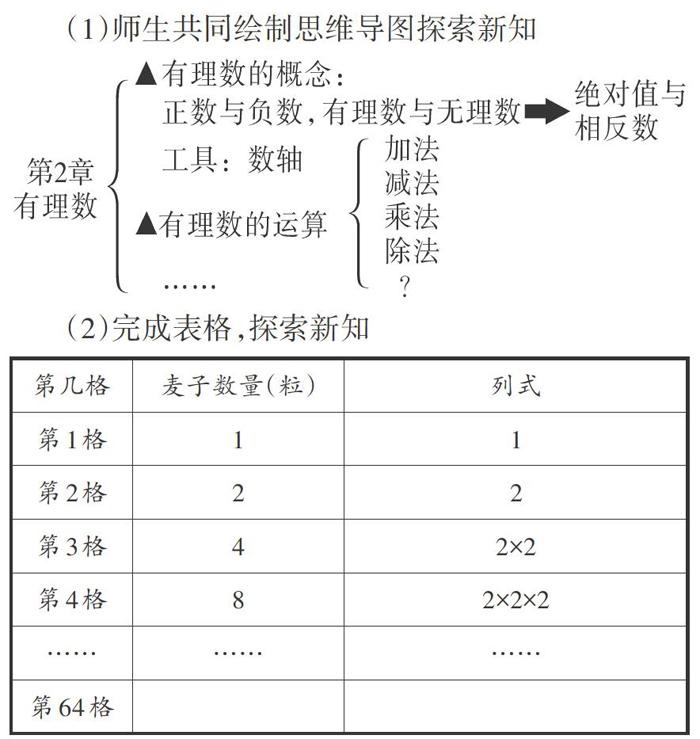
(1)师生共同绘制思维导图探索新知
(2)完成表格,探索新知
评析:利用思维导图将所学知识进行回顾,将知识在“面”上打开,连成“线”,在“点”上分析,让学生发现现有的知识储备并不能解决问题,从而产生强烈的探知欲,在此基础上展开新知的学习.在新知教学过程中,让学生经历 “知识是怎样形成的?”的问题预设和解决过程,在这个过程中“类比”乘法的本质理解乘方的本质,再教学乘方的定义及有关概念,引导学生从本质上理解[an≠an],让学生用幂来表示表格中的式子,将知识的易错点和混淆点在本质上厘清.
3.理解本质,运用新知
辨析 (-4)2、-42的区别与联系,并分别指出它们的底数和指数.
评析:在这个环节中,带领学生体验新知应用过程中的矛盾冲突点,并让学生运用所学的相反数知识以及“整体思想”解决矛盾冲突.这是一个旧知唤醒以及新知应用的过程,学生在无形中将零散的知识点串成线、织成网,进而达到了“面”的统一.本环节回答了“知识学后有什么用?”的问题.
4.寻求变式,提升认识
故事续编:正当国王为拿不出那么多粮食而犯愁的时候,宰相哈哈大笑了起来,说:“尊敬的陛下,能为您发明国际象棋是我的荣幸,刚刚我和您开了个玩笑.要不这样吧,陛下,请您在这张棋盘的第1个小格里,赏给我1元硬币,在第2个小格里给第1个小格的一半钱数,第3小格给第2小格的一半钱数,以后每一小格的钱数都是前一小格钱数的一半.请您把棋盘上64格的钱,都赏给您的仆人吧!”这下国王放聪明了,细细算了起来,算完后,他和宰相不约而同地笑了起来.同学们,你知道他们为什么笑了吗?
尝试:学了本节课的知识,你能创编一些数学小故事吗?
评析:故事续编,首尾呼应,引导学以致用,在故事中寻找数学的奥秘.同时,将课堂还原到生活中,这时学生已经不再是用冗长的乘法式子来表示,而是用简洁的幂来表示.引导学生用所学的数学知识去解决问题,提高学生的应用意识.本环节回答了“知识向哪里去?”的问题.至此,“知识从哪里来?知识是怎样形成的?知识学后有什么用?知识向哪里去?”串起了一条完整的教学活动主线.
数学课程目标从注重“双基”到三维目标,再到核心素养目标,将数学教学定位到育人的终极目标上.让学生将思维过程、方法策略内化为解决问题的基本认识、基本素质、基本态度及基本思想.而这些素养具体在学生身上怎么体现?在课堂教学中如何落实?教师必须说清楚、讲明白、做到位,这也是笔者将长期探索的问题.
“预设”的完美不及“生成”的精彩.经验丰富的教師会多角度、多维度地紧扣学生的学习实际设计教学预设,通过提问、追问、操作、讨论等形式完成预设目标.但是课堂的精彩来自于课堂的生成.在课堂的小结部分,有学生阐述了“乘方只是书写比较简单,但是运算还是要依靠乘法计算”的理解;有学生提出了疑问:“几个相同的数的加法可以用乘法表示(2+2+2=3×2),几个相同数的乘法可以用乘方表示(2×2×2=23),那么几个相同数的减法(2-2-2)、除法(2÷2÷2)可以怎么表示呢?”还有学生针对本节课的思维导图,提出了“是否还有第五种有理数的运算方法?”的问题……这些精彩的课堂生成补全了“点”,延长了“线”,拓展了“面”,健全了“体” .
[参考文献]
罗增儒.核心素养与课堂研修[J].中学数学教学参考,2017(23):14-20.
(责任编辑 陈 昕)

