砂-锯末混合模型土的动力特性试验研究

李雪菊,潘旦光

(北京科技大学 土木工程系,北京 100083)

0 引言

在地震作用下,无论地下结构、地面结构均存在土-结构相互作用。在强震作用下,土体易于进入非线性及结构存在提离和滑移等非线性影响,土-结构相互作用问题非常复杂。为验证计算模型和计算理论的合理性,常采用振动台试验进行验证。但是土-结构相互作用振动台模型试验面临的一个问题是无法使结构和土同时满足重力加速度的相似比,因此,实际试验时,对于结构部分采用配重进行设计,而土体则根据频率相似用模型土。砂-锯末混合模型土易于得到不同剪切波速而成为较常采用的模型土之一。孙利民等[1]采用锯末∶砂为1∶3的砂-锯末混合模型土进行了超大跨斜拉桥多点振动台试验研究。袁勇等[2]采用1∶2的砂-锯末混合模型土进行了超长沉管隧道土-结构相互作用振动台试验,楼梦麟等[3]采用1∶3.23的砂-锯末混合模型土研究了土-结构相互作用对振动控制的影响。

对于实验系统而言,砂-锯末混合模型土所构成的土体就是结构系统的场地,而场地条件显著地影响结构的地震反应[4]。由于锯末的存在将改变土体的力学特性,为更好的理解振动台实验中结构的动力反应现象,以及采用数值方法更好的还原振动台实验结果,需要确定模型土的非线性参数。

土体的动力特征影响因素众多,土的类型、密实度、孔隙比、围压、加载频率、固结比等都将影响土体的非线性参数[5-7]。燕晓等[8]和尚守平等[9]通过试验对锯末和砂配合比为1∶1～1∶20所配制的模型土的动力特性进行了研究。目前的常规振动台实验中,常采用的锯末和砂的比例在1∶2～1∶5之间,因此本文以锯末和砂按1∶3的质量比配制的模型土为研究对象,根据《土工试验方法标准规范》(GB/T50123-2019)[10]对该类模型土进行动三轴实验研究,初步探讨模型土在循环加载过程中动应力-动应变的变化特点及动弹模/阻尼比随应变的变化规律。可供类似试验研究参考。

1 试验概述

1.1 试验仪器及试样

试验采用英国GDS公司生产的新型伺服电机控制式动三轴仪(DYNTTS)。试验测定的剪应变范围为10-4～10-2。试验所用土样为锯末-砂按1∶3的质量比配制而成的模型土,直剪试验表明模型土的性质接近砂土,烘干法测得其天然含水率为12.34%,设计密度为0.985 g/cm3。试样为39.1 mm×80 mm的实心圆柱,制样时,计算出所需用土的质量,分5层击实成型。

1.2 试验方案

试验时,围压为100 kPa,荷载频率为1 Hz。试验采用Δσd=10 kPa分级加载,试验开始时先对试样施加预定围压排水固结30 min,固结完成后,在不排水条件下,施加逐级增加幅值的正弦波循环荷载,每级荷载施加10个循环[11-13]。加载曲线如图1所示。

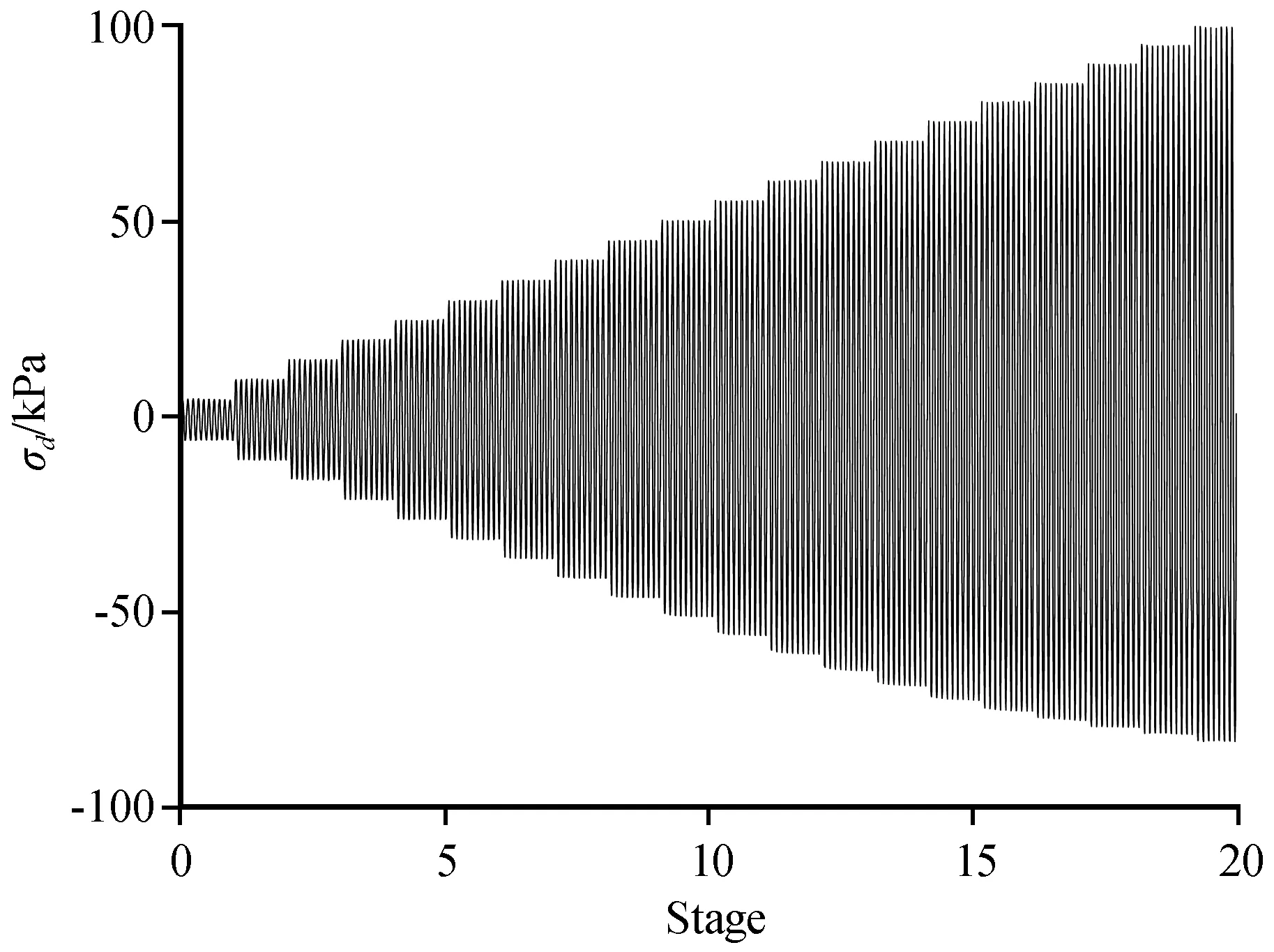
图1 加载曲线Fig.1 The loading curve

1.3 数据处理原理

理想的应力-应变滞回圈如图2所示,阻尼比与动弹性模量Ed的计算公式为:

图2 理想的应力-应变滞回圈Fig.2 The ideal stress-strain hysteresis loop

λd=W/4πWt

(1)

Ed=(σdmax-σdmin)/(εdmax-εdmin)

(2)

式中:W为滞回曲线A,B,C,D所包含的面积;Wt为三角形AOE的面积;σdmax、σdmin分别表示同一次循环荷载中最大、最小轴向动应力;εdmax、εdmin分别表示同一次循环荷载中最大、最小轴向动应变。由此可得土体的动剪切模量和动剪应变为[14]

(3)

式中:Gd为动剪切模量;γd为动剪应变;μ为泊松比。

2 试验结果

2.1 滞回圈特性研究

在加载过程中,各级加载下第5次循环的滞回圈如图3所示。将加载过程中应力-应变的峰值点连线,可得骨干曲线。由骨干曲线可知,在1～12级加载时,应变随着应力的增加而增加,但是当应变达到1%后,应力增加,应变反而减少而出现反弯点,这是由于此时土样出现了颈缩而发生了破坏,如图4所示。因此,后面仅分析试样破坏前的试验结果。

图3 应力-应变滞回圈Fig.3 Stress-strain hysteresis loop

图4 破坏后的试样Fig.4 Damaged sample

由图3(b)可知,应力-应变滞回曲线都不是标准的椭圆状,在循环荷载加载初期,面积较小且形状对称,各滞回圈近似于柳叶形,随着荷载幅值的增加,动应变幅值增大,滞回圈面积逐渐增大且呈现出不对称性,表明阻尼比变大,且滞回圈整体形状发生了改变,滞回圈中部下凹,逐渐向新月形发展,这说明随着荷载级数的增大,滞回圈形状会发生改变。

应用公式(4)对第2级和第12级的应力应变进行归一化,归一化后的应力-时间与应变-时间曲线如图5所示。

(4)

式中:Ai为应力、应变的原始数据;Aj为归一化后得到的应力、应变数据。

由图可知:在加载过程中,第2级荷载的应力相位几乎与应变相位并行,这说明在第2级加载时土样基本处于线性阶段,基本不产生的塑性变形,滞回圈的割线斜率较大,即动弹性模量较大;滞回圈面积较小即阻尼比较小,如图3(b)所示;对于第12级荷载,在加载阶段,应力较小时,应力应变基本重合,随着应力的增大,应变滞后于应力,反向卸载阶段,应变都滞后于应力,此时产生的塑性变形增大,由此导致图5(b)中应力-应变滞回圈在加载阶段基本水平而反向后中部下凹出现新月形的滞回圈,滞回圈面积增大,土样的阻尼比增大,动弹性模量减小。

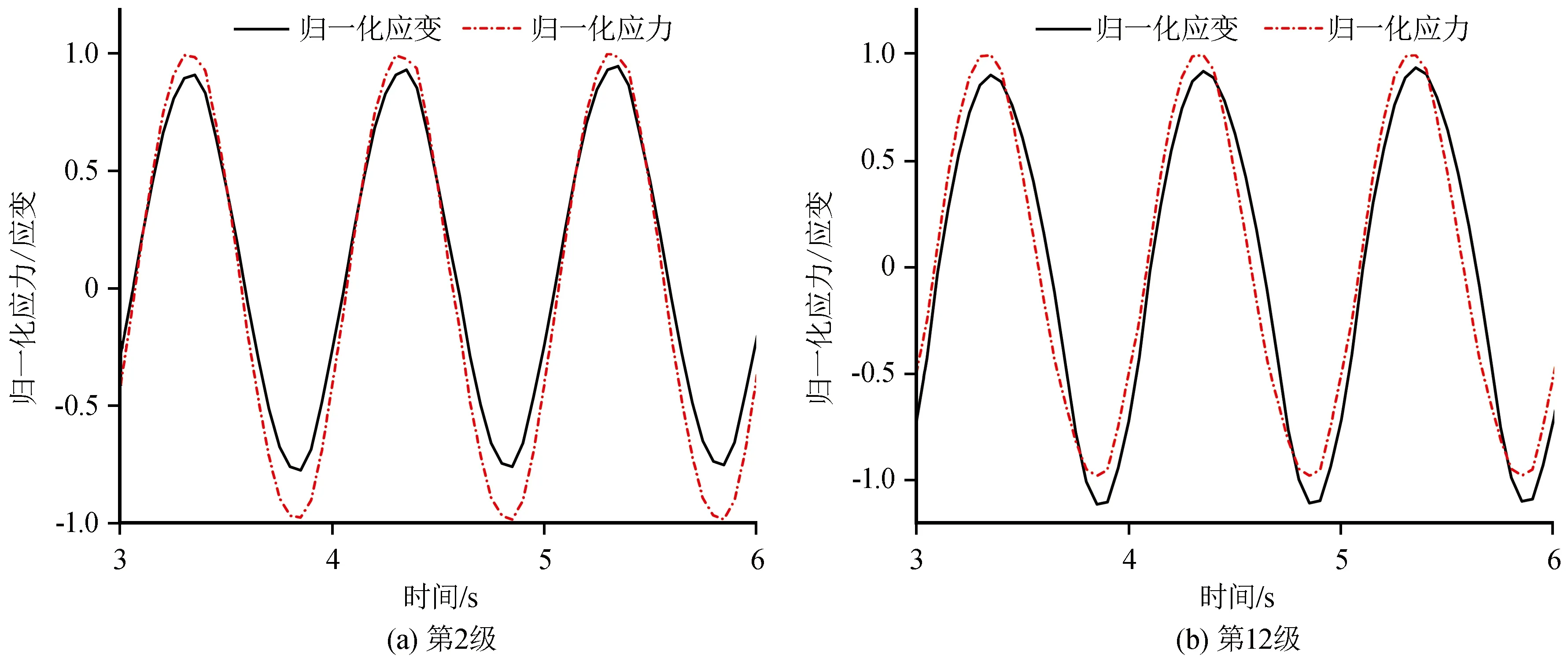
图5 应力/应变-时间曲线Fig.5 The curve of stress/strain-time

2.2 动力特性变化过程

第10级加载所得的应力-应变曲线如图6所示。从图中可以看出在同一级加载过程中,滞回圈逐渐向应变增大的方向发展表现为滞回圈逐步向右平移。

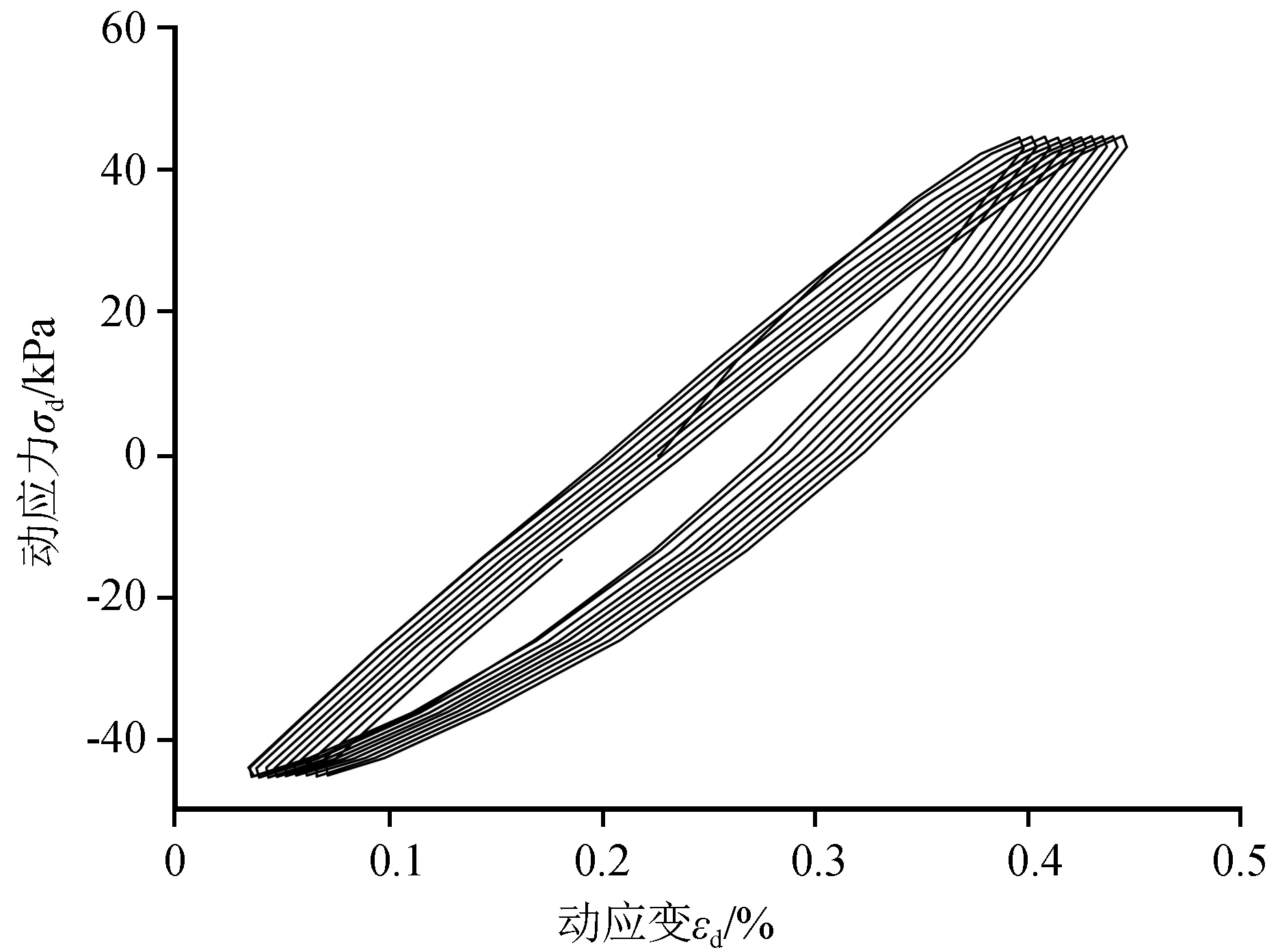
图6 应力-应变曲线(第10级)Fig.6 The curve of stress-strain

对每一级加载,动剪切模量和阻尼比随循环次数的变化规律如图7所示。

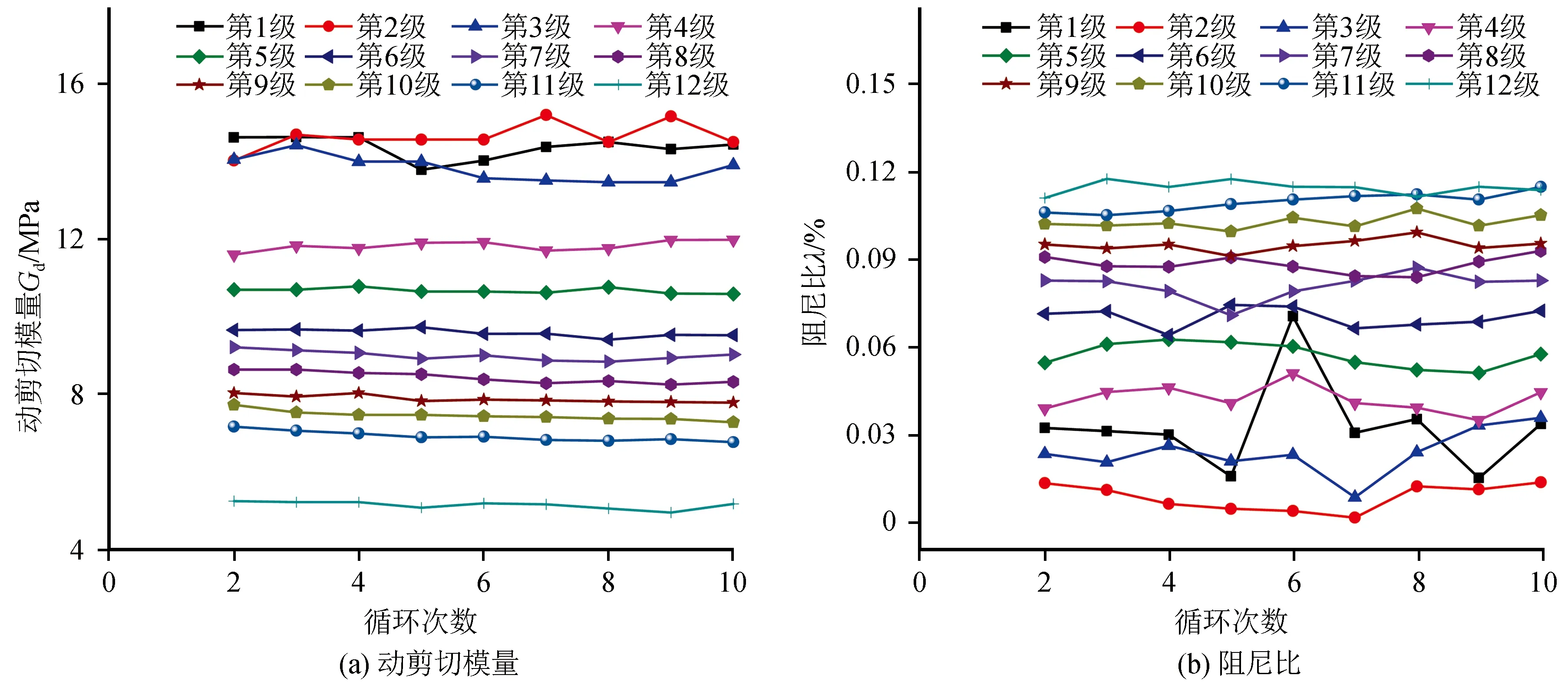
图7 各级荷载下动力参数与循环次数关系Fig.7 Relationship between dynamic parameters and cycle number under different loads

从图中可以看出:(1)初始加载阶段土样开始压密闭合,且第1级轴向荷载较小,试验仪器较难控制精度,因此第1级动剪切模量和阻尼比数据的离散性较大,此后各级曲线逐渐趋于稳定。(2)从总体上看,随着荷载级别的增大,模型土的动剪切模量曲线向下偏移,而阻尼比曲线呈上移趋势,即动剪切模量随剪应变的增加而减小,阻尼比随之增大,符合一般规律。(3)在同一荷载级别下,不同循环的动剪切模量基本为常量,而阻尼比呈现波动趋势。这说明当每一级加载,各循环的动剪切模量和阻尼比的变化不大,因此各级曲线的动剪切模量、阻尼比均值即可作为本级荷载下引起的最终动剪切模量和阻尼比。

根据《扎赉特旗国民经济和社会发展第十二个五年规划纲要》，对2015年区域内各行业需水进行预测（见表3）。由表3可见，项目区地下水可开采量能够满足节水增粮行动项目对地下水的需求。

3 砂-锯末混合模型土的动参数

图8中的离散点为各级加载下的平均动剪切模量和阻尼比。由此可知,锯末-砂混合模型土的动剪切模量比和阻尼比随动应变有渐近关系,可采用双曲线模型对模型土的动剪切模量比和阻尼比数据进行拟合,根据Hardin-Drnevich模型,动剪切模量和动剪应变的关系可用下式表达:

(5)

式中:a=1/Gmax,b=1/τmax,γr=a/b=τmax/Gmax称为参考应变。

阻尼比与动应变幅的表达式如下:

λ/λmax=(γd/(γr+γd))α

(6)

式中:λmax为最大阻尼比;α为阻尼比参数。

对实验数据,用式(5)和式(6)进行拟合,可得拟合参数为Gmax=15.923 6 MPa,λmax=0.186 466,γr=0.001 944,α=0.909 3。

为分析砂-锯末混合模型土与一般砂土模量、阻尼比的差异性,图8中将砂土的动剪切模量和阻尼比[15]也绘出,以做比较。

图8 Gd/Gmax、λ/λmax与γd关系曲线Fig.8 The relation between Gd/Gmax、λ/λmax and γd

从试验结果可看出,模型土和砂土模量比和阻尼比差异明显。模型土的G/Gmax及λ/λmax变化曲线与砂土的形态基本一致,模型土的模量比偏小,阻尼比偏大。这表明与砂土相比,模型土由于锯末的存在,模型土的弹性性能更差,而耗能更快。

在进行模型试验时,以锯末为主要成分的模型土密度较小,可有效的解决振动台承载力不足的问题,且可以使模型试验模拟更大范围的地基土域,从而尽量减少模型试验中地基土边界效应的影响。本文给出了的模型土的动应力-应变关系模型及其参数变化规律可供类似模型试验及算法验证参考,此外模型试验设计时应考虑循环次数的影响以及此类模型土的特性。

4 结语

针对砂-锯末混合模型土,采用动三轴试验研究了模型土的滞回圈特性以及动剪切模量和阻尼比随循环加载次数的变化规律,并对比分析其动力特性与一般砂土的差异性。根据试验结果可得出了以下结论:

(1) 模型土在荷载循环过程中,加载初期,加载段表现出应变基本同步于应力的现象,滞回圈呈柳叶型,随荷载级别的增加表现出应变超前应力的现象,滞回圈的面积越来越大,逐渐发展为新月型。

(2) 同一荷载级别下,模型土不同循环的动剪切模量基本为常量,而阻尼比上下波动;随荷载级别的增大,动剪切模量均值减小,阻尼比均值增大。

(3) 模型土的动力参数曲线分布形态与一般砂土类似,但模型土的动剪切模量比更小,阻尼比更大。