特征周期相关性分析

张嘉琦,刘文锋,2

(1.青岛理工大学土木工程学院,山东 青岛 266033;2.山东省绿色建筑数字化建造技术工程实验室,山东 青岛 266033)

0 引言

特征周期是反应谱曲线下降段起点对应的周期,影响反应谱的谱型。特征周期可基于地面运动记录确定。近年来,赵培培等[1]对川陕甘宁地区2 388条强震地震记录采用差分进化算法确定了加速度反应谱的特征周期,得出这一地区大震远场反应谱特征周期的统计结果较我国抗震设计规范规定的反应谱特征周期值偏高;郭明珠等[2]搜集美国西部地区的825条强震记录得出特征周期随场地的变软而增大,并且我国抗震设计规范中水平向特征周期取值比实际值偏低;齐玉妍等[3]收集北京、河北、天津94个强震动台站的记录结果进行对比,发现在震中距差别不大的情况下软弱土层台站相比基岩台站的地震反应谱特征周期偏大;赵万松等[4]搜集美国西部地区166个有详细钻孔资料台站场地上的1 237条水平方向强震记录计算反应谱的特征周期,研究特征周期取值随场地类别、震级、震中距的变化特征,得出特征周期随着场地类别的提高而增大,震级对特征周期的影响要大于震中距,建议抗震设计规范中各类场地上各地震分组内的特征周期值在原来的基础上增加0.05 s,并应适当考虑地震动峰值加速度对特征周期取值的影响;刘文锋等[5]采用概率法对特征周期进行统计分析,得出特征周期与震级、场地类别和震中距的关系比较复杂且离散,特征周期呈区间分布规律,区间内部定量关系较难确定。

从抗震设计规范设计角度看,也是基于地面运动记录确定特征周期[6]。在美国,抗震设计规范ATC 3-06[7]采用有效峰值速度EPV与有效峰值加速度EPA的比值确定特征周期,其中EPA取5%阻尼比加速度反应谱高频段(0.1～0.5 s)的平均值除以2.5,EPV取5%阻尼比加速度反应谱中频段(0.5～2 s)的平均值除以2.5;美国抗震基础规范FEMA-450[8]根据1 s和0.2 s时反应谱的特征参数确定特征周期,即周期为1 s和0.2 s处的设计地震动加速度值之比;2017年新颁布的ASCE7-16规范[9]采用了周期1 s和0.2 s时反应谱的有效峰值加速度与场地系数相结合的方法,确定反应谱特征周期。在我国,《地震动参数区划图(GB18306-2015)》[10]也是按场地环境与地震综合效应来确定特征周期,但与ATC3-06中固定频段求取EPA和EPV的方法不同,区划图具体分析每条反应谱求取这两个有效值时不将频段固定[11]。《建筑抗震设计规范(GB50011-2010)》[12]是基于地表强震记录,获取强震记录台站的地质剖面、近远震等信息,按场地类别和设计地震分组对强震记录进行分类,计算各类场地的平均反应谱,并作平滑处理,计算场地反应谱特征周期,并进行特征周期区间分组。因此,特征周期映射了场地类别和地震分组,所以我国建筑抗震设计规范规定特征周期根据场地类别和地震分组确定。反过来,如果能根据实测地震动记录求出特征周期,结合所属的设计地震分组,则可由此大致判断出该场地的场地类别,进而可为抗震设计时程分析中地面运动记录的场地类别提供参考。

由于反应谱是地面运动记录最大响应的映射函数,基于地面运动记录计算特征周期,将反映反应谱全域谱型拐点特征。本文采用6种基于地面运动记录的特征周期计算方法,对1 491条地震动记录进行特征周期计算,分析计算结果的分布和相关性。

1 特征周期的计算方法

我国《建筑抗震设计规范(GB50011-2010)》和美国抗震设计规范ATC3-06都是在大量强震观测记录的分析基础上得到规准化后反应谱下降段的起始周期,具有一定的概率保证。单条强震记录特征周期标定法是从一条强震记录加速度反应谱通过简化的数学表达式直接计算得到。常用的特征周期计算方法主要有以下几种:

(1) ATC3-06规范规定特征周期:

(1)

式中:EPV为有效峰值速度;EPA为有效峰值加速度。

(2)ASCE7-16规范规定特征周期:

(2)

式中:SD1、SDS分别表示周期在1 s和0.2 s时反应谱的谱值;Ss、S1分别表示周期在1 s和0.2 s时反应谱的有效峰值加速度;Fa、Fv代表场地系数。

(3)概率法

在规定概率下,能反映峰值区间效应最大值对应的周期就是特征周期。概率可用平台化的反应谱与初始反应谱的面积比表征,可表达为:

Tα%=Tmax(Sα%)

(3)

式中:Sα%是代表α%面积比的平台化的反应谱曲线。本文采用的概率为97%。

(4) 峰值法

峰值法是根据反应谱或规准谱最大值对应的周期来确定特征周期。其表达为:

Tβmax=T(βmax)

(4)

式中:βmax为方法系数最大值。

(5)峰值折减法

折减法是对反应谱或规准谱最大值进行折减,以对应的周期来确定特征周期。

(5)

(6)平滑法

平滑法是对一定水准的反应谱或规准谱的周期值进行平滑化处理。其表达为:

(6)

式中:Ti为5%阻尼比加速度反应谱等间距离散周期;Sa(Ti)为Ti对应处的谱加速度;PGA为峰值加速度,取Ti≥T(Sa/PGA≥1.2)。

2 六种计算方法的特征周期分布

实际强震记录是对地震作用的直接了解,各国抗震设计规范中均以此为依据。本文的地震记录取自美国太平洋地震工程研究中心(http://peer.berkeley.edu),覆盖了美国、日本、土耳其及中国台湾,共包括8个地震事件。经筛选确定较完整的1 491个地震记录(表1)。

表1 地震记录的基本信息及数量Table 1 Basic information and quantity of seismic records

2.1 全部特征周期分布

本文采用前述6种方法对所搜集的1 491条地震动记录进行计算,所得到特征周期的分布见图1。另建立三维坐标分析特征周期计算方法在设定0.1 s为一个区间内的数量分布关系,得到图2。由图1、图2可以看出特征周期短周期的数量分布多而长周期的数量分布较少;在同一地震动记录条件下,6种方法所计算的周期值不完全相近;随地震动序号的改变,6种方法的计算结果同时出现相似的波动,表明6种计算方法具有相关性。同时参照我国抗震设计规范表5.1.4-2按0～0.20 s、0.20～0.35 s、0.35～0.45 s、0.45～0.65 s、0.65～0.90 s、0.90～1.2 s、1.2～2 s、2～3 s、>3 s划定区间,统计区间内周期分布百分比,见图3。1 491条地震动记录因场地地震环境等因素计算得到的特征周期分布覆盖面较广,0～6 s都有分布,其中在0.20～2 s内分布相对平均,0～0.20 s、2～3 s、>3 s鲜有分布,但主要集中在0.20～1.2 s,占总数的80%。表2统计了特征周期在0～6 s内的累计分布,可以看出除峰值法的特征周期多分布在相对较低区间外,其他5种方法在数量上累计分布总体上无较大差异。

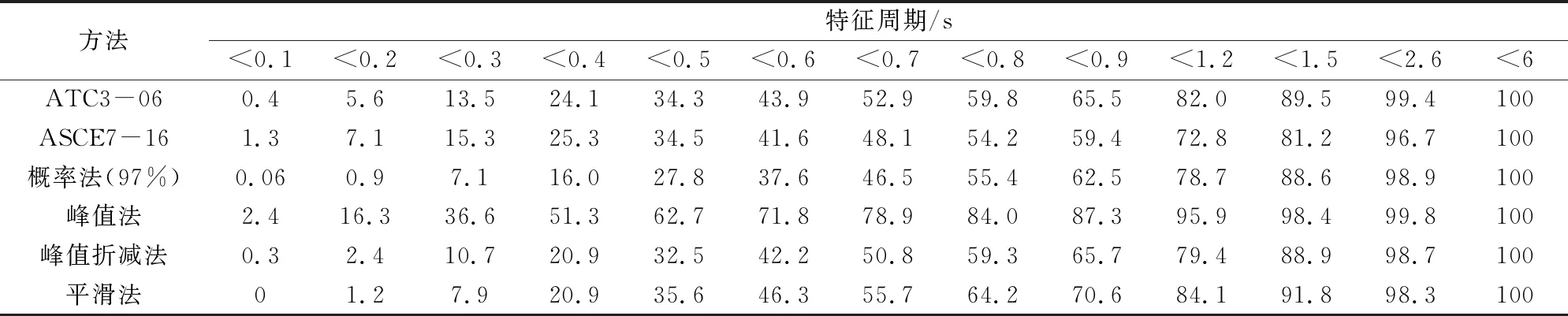
表2 累计特征周期分布Table 2 Distribution of accumulative characteristic periods

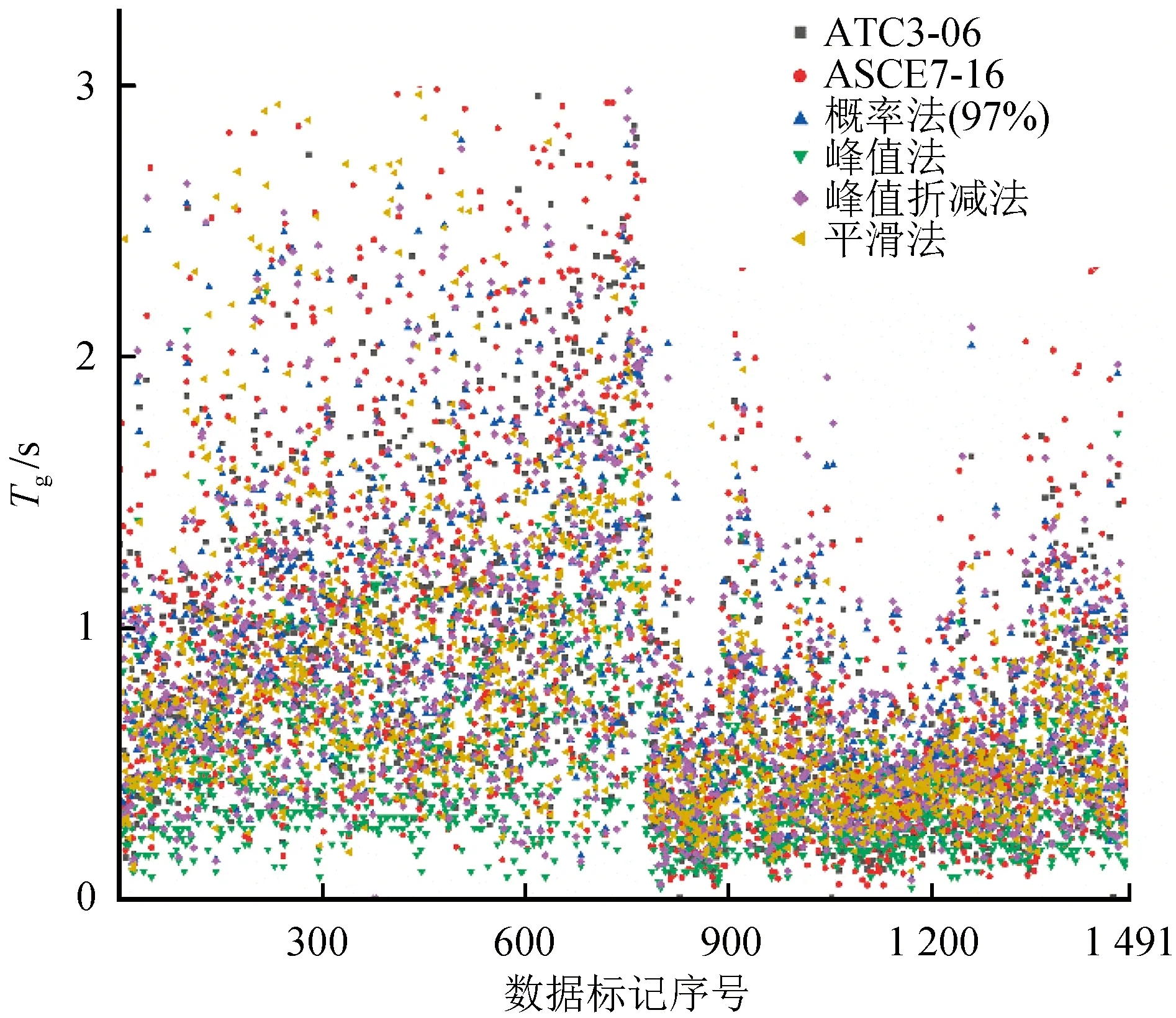
图1 特征周期分布图Fig.1 Distribution of characteristic periods

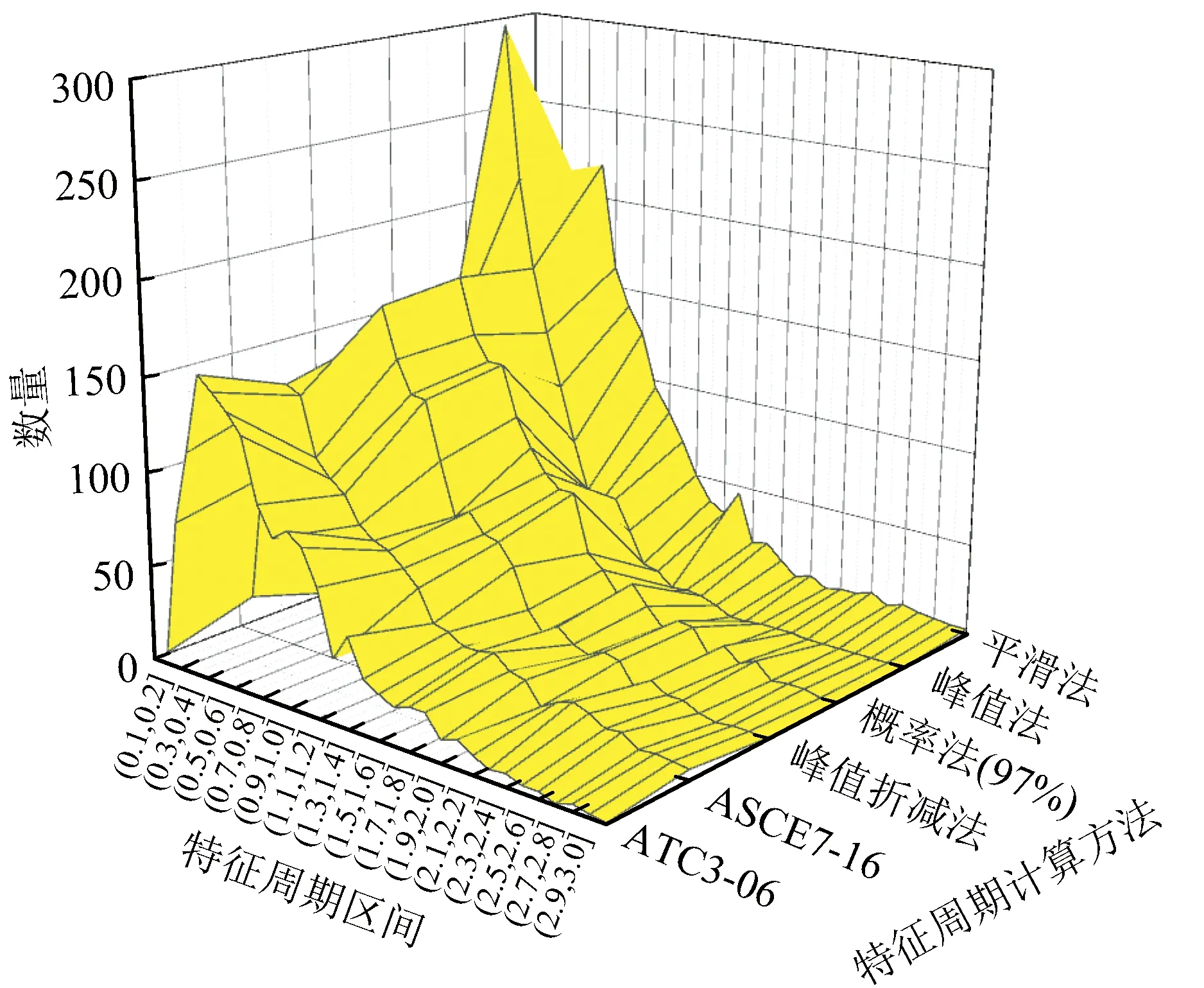
图2 特征周期的数量分布Fig.2 Quantitative distribution of characteristic periods

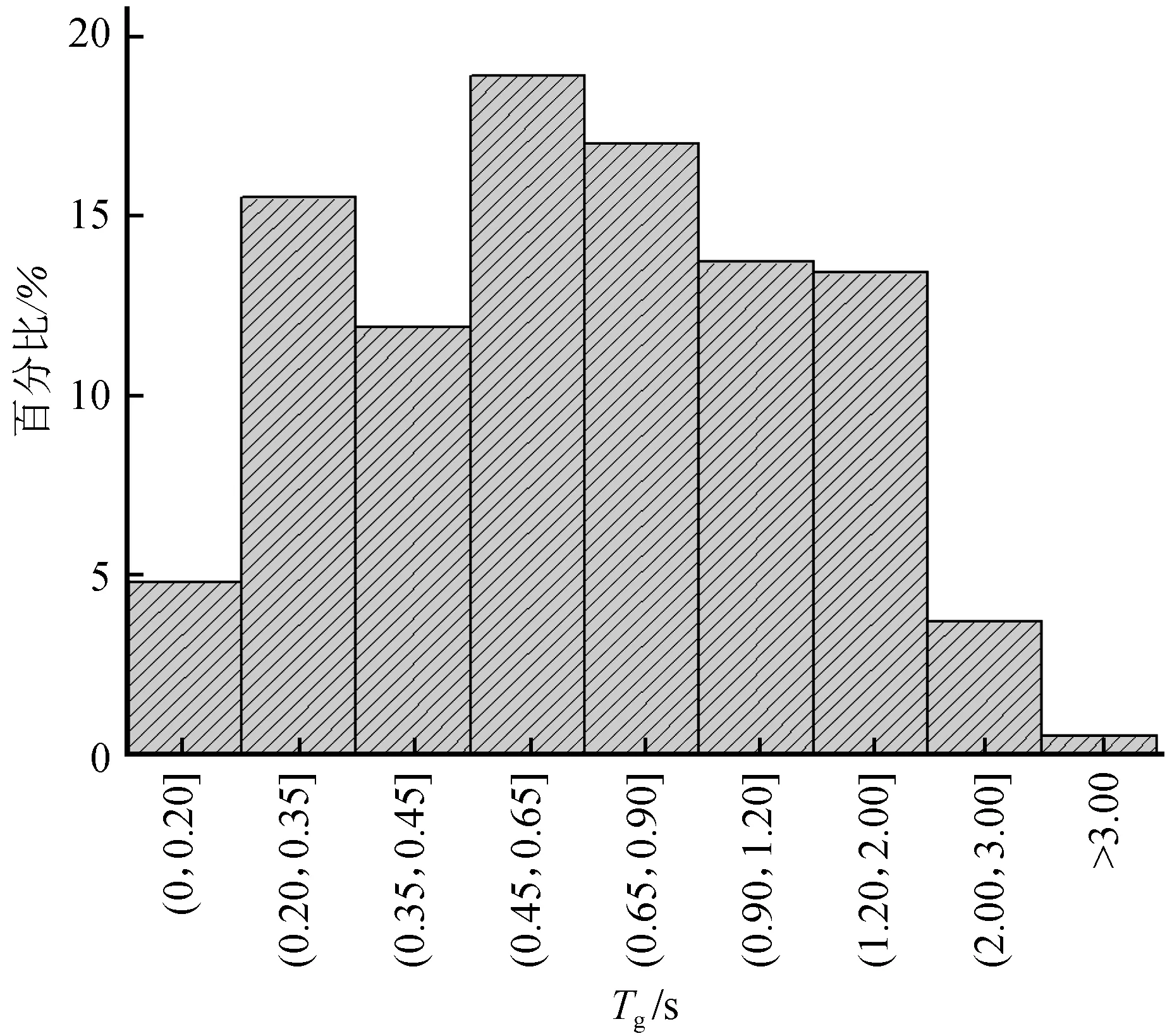
图3 周期区间分布百分比Fig.3 Distribution percentage of characteristic periods

2.2 不同方法的特征周期分布

6种计算特征周期的方法都间接表征设计反应谱与实际地震动反应谱接近程度,特征周期确定的越合理证明对工程建设实际应用越可靠。图4给出了6种方法特征周期分布的点云图(3 s内),可以发现6种方法因数学表达形式和揭示数学统计规律计算结果有较大差异。统计周期区间0～0.20 s、0.20～0.35 s、0.35～0.45 s、0.45～0.65 s、0.65～0.90 s、0.90～1.2 s、1.2～2 s、2～3 s、>3 s内6种方法所计算的数量分布如图5所示,可以看出ATC3-06方法、ASCE7-16方法、概率法(97%)、峰值折减法与平滑法特征周期主要分布在0.2～2 s之间,其中ATC3-06方法在0.45～0.65 s、0.65～0.90 s和0.90～1.2 s区间占比各达15%以上;ASCE7-16方法分布在0.20～0.35 s、0.45～2 s之间共占总数的74%;概率法(97%)在0.20～2 s占总数95%;峰值折减法与平滑法在0.45～0.65 s和0.65～0.90 s区间上相似，均在20%左右;峰值法特征周期主要分布在0.20～0.35 s区间内,占30.7%。

图4 不同方法的特征周期分布Fig.4 Characteristic period distribution of different methods

图5 6种方法在周期区间分布的百分比Fig.5 Percentages of 6 methods in periodic interval distribution

2.3 不同地震事件的特征周期分布

特征周期从统计学意义上宏观反映着场地特征。基于本文所采用的8个地震事件利用6种方法计算的特征周期分布,得到图6(3 s内)。图7为8个地震事件地震动记录周期分布区间百分比。

从图6和图7可以看出,不同地震事件的特征周期在区间上分布不同,Imperial、Northridge、Morgan Hill、Kobe和Loma Prieta特征周期主要分布在抗震规范所划定的特征周期区间0.20～0.90 s内;Kocaeli和Chichi特征周期分布在0.20～2 s之间;Borrego Mountain特征周期数量在较长周期0.90～2 s分布占比接近50%。不同地震事件与地震机制、地震波传播和场地因素等有关,特征周期在地震事件所包含的地震动记录中呈区间规律分布,且其分布随着地震事件不同而出现小范围波动,基于地面运动记录宏观反映场地对特征周期的影响。

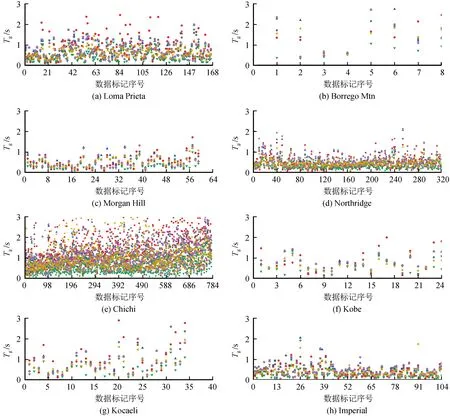
图6 8个地震事件的特征周期分布Fig.6 Characteristic period distribution of 8 seismic events

图7 8个地震事件的地震动记录周期分布区间百分比Fig.7 Percentages of 8 seismic events in periodic interval distribution

3 特征周期相关性分析

为判断6种方法数学表达式之间的相关性,继续基于地面运动记录用Spearman相关性系数对6种方法计算结果序列的秩次大小作相关性分析。计算公式为

(7)

式中:rs为相关系数;di为两列变量的等级之差;n为样本容量。相关系数取值范围在-1和+1之间,即|rs|≤1。|rs|越接近1,则表明现象相关程度越高。当rs介于0.8～1.0时为极强相关,当rs介于0.6～0.8时为强相关,当rs介于0.4～0.6时为中等强度相关,当rs<0.4时为弱或不相关。分析过程如下:

以1 491条地震动记录作为输入,采用ATC3-06方法、ASCE7-16方法、概率法(97%)、峰值法、峰值折减法、平滑法计算每一地震动反应谱的特征周期,每种方法的计算结果按数据标记顺序组成一列,共组成六列,在SPSS 25.0软件中对6种方法计算的特征周期序列进行相关性计算。计算的Spearman相关性系数统计于表3中。

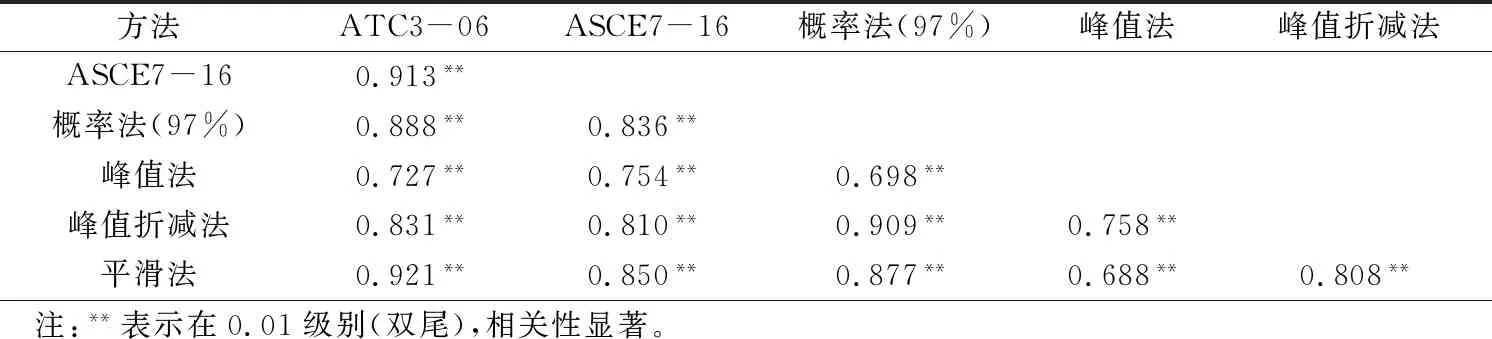
表3 Spearman相关性系数表Table 3 Spearman correlation coefficients

相关性结果显示:(1)ATC3-06方法与ASCE7-16方法相关性系数达到了0.913,可见美国规范的特征周期取值考虑了场地因素。(2)ATC3-06方法与平滑法、概率法(97%),概率法(97%)与峰值折减法有极强的相关性,Spearman相关性系数都达到0.9以上,当采用ATC3-06方法失真时,可考虑选用另外平滑法、概率法(97%)方法来替代。(3)概率法(97%)是反应谱从平台段转向下降段的面积占整个反应谱的面积比确定特征周期的,与ATC3-06方法、ASCE7-16方法、峰值折减法、平滑法的Spearman相关性系数都达到0.8以上,说明其具有较好的鲁棒性。(4)峰值法相对于其他5种方法来说,相关程度相对偏低,峰值法与平滑法在数量分布上特征相似但在相关性分析中其相关性程度相对较低。

4 结语

本文以1 491条地震动记录为基础,分别用不同方法、不同地震事件统计分析了特征周期分布,从特征周期分布和计算方法的相关性分析了6种特征周期计算方法的相关性。分析结果得到:

(1) 基于地面运动记录的特征周期映射了反应谱曲线下降段起点对应的周期,间接反映了场地类别、震中距等地震环境信息。

(2) ATC3-06特征周期映射了区段谱速度与区段谱加速度之比;ASCE7-16特征周期在简化区段谱速度与区段谱加速度之比的基础上,又引入了场地系数Fa、Fv,更加凸显了场地效应对特征周期的影响;概率法(97%)以反应谱特征周期下包含的面积比映射特征周期。

(3) 6种计算方法8次地震计算的特征周期主要分布在0.2～1.2 s,占总数的80%,不同地震特征周期在0.2～1.2 s区间内的分布具有差异性,宏观反映场地对特征周期的影响。

(4) ATC3-06、ASCE7-16、概率法(97%)、峰值折减法、平滑法之间的Spearman相关性系数均已达到0.8以上,其中ATC3-06和ASCE7-16、ATC3-06和平滑法、概率法(97%)和峰值折减法的Spearman相关性系数已达到0.9以上,反映了这些方法的同源特征,均能较好地反映特征周期是反应谱曲线下降段起点周期的属性。