混凝土单桩对瑞利波的阻隔机理试验研究
赵大威,刘 航,2,刘晶磊,2,张 楠,2
(1.河北建筑工程学院 土木工程学院,河北 张家口 075000;2.河北省土木工程诊断、改造与抗灾重点实验室,河北 张家口 075000)
0 引言
近年来,我国经济建设稳步增长,伴随而来的振动问题也日益引起人们的注意。通常在建筑物的设计中,地震作为不确定因素同样夹杂在建筑物的结构稳定性设计中[1],但由于交通方式的改变,在原有环境中增加高铁、地铁等交通工具极大地影响建筑物的结构稳定[2]。爆破、强夯、打桩、轨道交通等人工活动产生的振动对古建筑的安全以及精密仪器的使用产生了严重的影响[3-5]。如何降低振动波对周围环境的影响是学者们研究的重要方向[6],通常阻断振动波的方法是在振动波的传播路径上设置屏障,屏障可分为连续屏障与非连续屏障[7]。空沟作为一种连续屏障,在土质较好的地层中可发挥较好的隔振作用。然而在实际的工程隔振中,由于土体稳定性以及工程造价等问题,空沟的深度受到限制[8],而当入射波的波长较大时,空沟的隔振效果则大大减弱,此时采用排桩进行隔振,则可不受地形的约束,同时也可达到良好的隔振效果。部分学者选择对主动隔振进行隔振效果的试验分析,然而在实际工程中,主动隔振并不是一种有效的经济手段,其花费往往巨大[9]。
国内外许多学者对排桩被动隔振时的隔振机理、隔振效果进了试验分析与数值模拟。在试验方面,Woods等[10]通过室外试验对单排桩的设计提供了准则,即桩径必须大于被屏蔽波长的1/6,然而在实际工程中,当波长较长时,桩径需要很大才能满足要求。高广运[11]通过数值计算与试验相结合的方法,突破了Woods提出的桩径大于1/6的理论,并取得了良好的隔振效果。孙成龙等[12]实测了排桩在铁路工程中的隔振效果,指出排桩的隔振效果并不是随着桩排数的增加而增加。在数值方面,Kattis等[13]运用频域边界元法研究了单排桩在三维层面上的隔振问题,指出桩间距是影响隔振效果的最重要的因素,并提出排桩可作为填充沟来进行隔振。Avlies等[14-15]采用波函数展开法研究了单排桩对P波、SH波、瑞利波的振动隔离问题,指出桩的刚度越强,隔振效果越好。徐平等[16]运用波函数展开法研究了单排桩对振动波的隔离问题,指出隔振效果随着桩间距的减小而提高。李志毅等[17]以瑞利波散射积分方程为基础,在三维层面对多排桩远场被动的隔振效果进行了分析,结果指出多排桩的桩径与桩间净距对隔振效果的影响小。刘中宪等[18]采用IBIEM的方法研究了多排桩对P波、SV波的隔离问题,指出桩径、桩间距的优化设计能有效提高隔振效果。孙苗苗等[19]从多重散射理论的角度出发,研究了任意排列、任意截面多排桩对P波、SV波的散射问题,结果表明桩间距、排间距、桩材料均对隔振效果有较大的影响。
以上学者的研究中,隔振机理以及隔振效果是研究的主要内容,本文在此基础上,通过室外试验并将单桩尺寸与瑞利波波长建立联系来分析当单桩几何参数变化时桩周土体的振动区域变化情况,对单桩周围土体的振动区域进行了研究。
1 理论基础
振动波在土体中的传播主要有P波、S波和R波,而S波在空间上的振动可分解为SH波与SV波。当P波与SV波相互干涉时,在介质表面则形成了瑞利波。瑞利波(R波)以其衰减速度慢的特点在土体表面进行传播时,对地表振动的影响最大。
当在土体中设置单桩时,瑞利波遇到单桩会发生绕射、透射、散射等现象[20],而绕射波则可分为桩边绕射与桩身绕射,如图1所示。然而单桩并不能阻挡全部的波能量,瑞利波仍会以某种方式影响单桩后面的土体。
在图1中,单桩桩前主要为反射波的作用,而在桩两侧则主要为绕射波,桩后的隔振效果则主要取决于绕射波与透射波的作用。

图1 振动波传播理论图Fig.1 Theoretical diagram of vibration wave propagation
2 试验概况
2.1 场地概况
为了防止人工振动与噪声对结果产生不利的影响,本试验场地位于郊区偏远地带。通过试验,确定了场地的土质主要为砂性土,同时为了消除土壤中的杂质以及边界效应对振动波的影响,在试验场地中间开挖出一个平面尺寸为2 m×4 m,深度为5 m的坑,并将原有场地砂子经过5 mm孔筛筛过之后回填坑内,在回填过程中已分层夯实。试验场地砂层含水率控制在13%~15%,密度控制在1.80~1.90 g/cm3。
2.2 仪器概况
在本文中,试验仪器采用WS-Z30型振动台控制系统,其中包括激振器、信号发生器、电荷放大器、功率放大器、加速度传感器(灵敏度为4 PC/ms-2,频率响应范围为0.2~8 000 Hz,质量为28.50 g,测量范围为50 m/s2)、数据采集控制仪等。试验仪器设备如图2所示。

图2 试验仪器Fig.2 Test equipment
2.3 试验安排
本试验中,激振器作为振源。由于正弦波输出稳定,且操作简单,故本试验采取的振动波类型为正弦波。试验频率的选择基于文献[20],为了使拟合方程的拟合程度更加准确,因此试验所采用的频率为30 Hz、60 Hz、90 Hz、120 Hz。采样频率设置为5 000 Hz,激振时间为5 s。在整个激振过程中,电荷放大器的数值始终保持一致。表1为本次试验的变量,传感器摆放见图3。

表1 试验变量及取值Table 1 Test variables and values
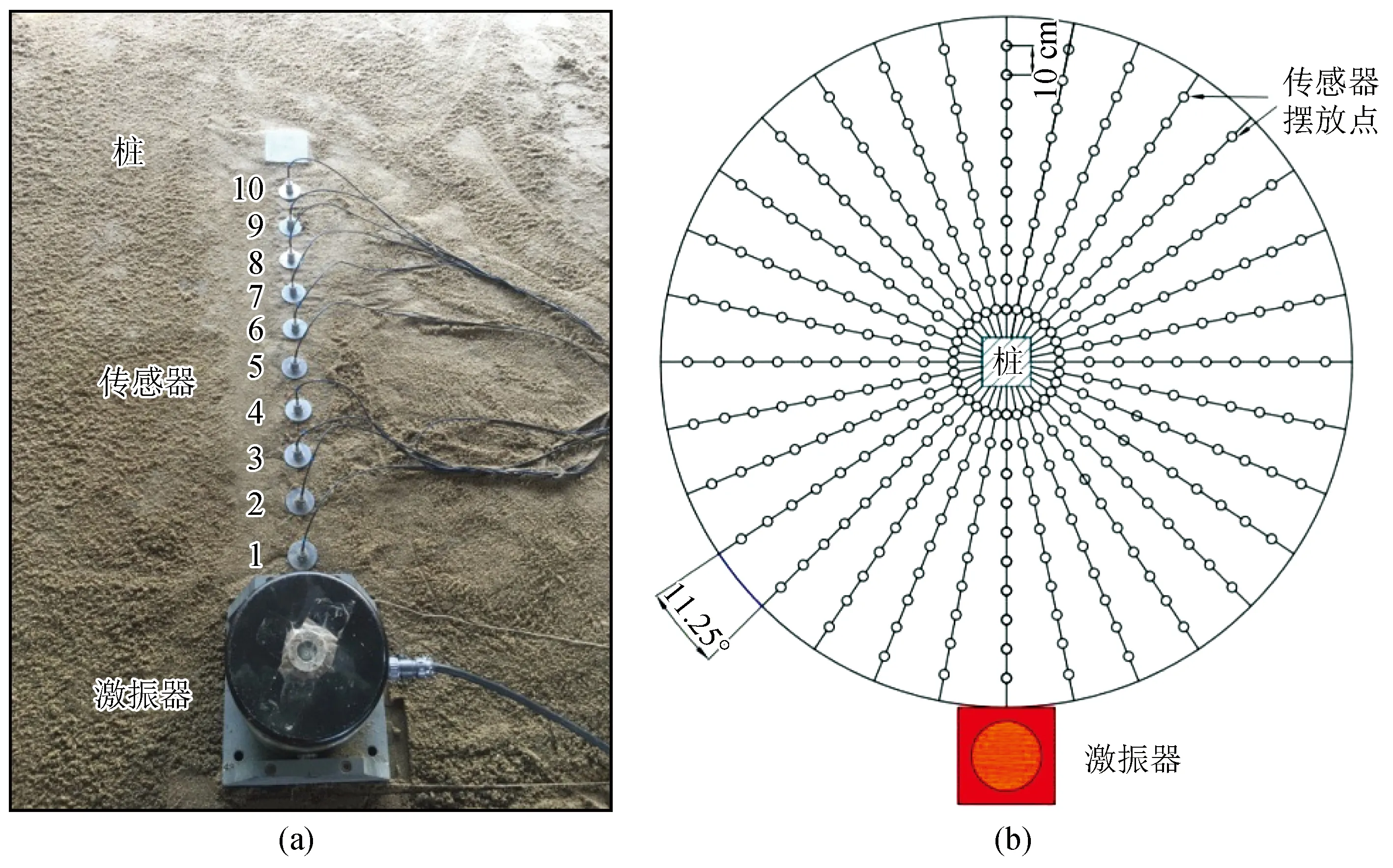
图3 传感器摆放详图Fig.3 Layout of sensors
3 试验评价指标
本试验通过绘制二维Ar等值线图来分析单桩周围振动区域的变化。同时Ar值越小则代表隔振效果越好[21]。其计算方法如下:
Ar=a1/a0
(1)
式中:a1表示设置单桩时各测试点的振幅加速度值;a0表示无桩时各测试点的振幅加速度值。
4 波长测试及数据采集
4.1 瑞利波波长的测试
本文选用表面波普法[22]测试砂性土中的瑞利波波速。相关仪器摆放见图4所示。

图4 瑞利波波速测试Fig.4 Rayleigh wave velocity test
经过信号采集及处理,当激振频率为150 Hz时的相位差为147.45,且信号的相关性良好,经计算可得瑞利波的平均波速为109.99 m/s。瑞利波的波长可由公式2计算可得:
LR=VR/f
(2)
式中:LR为瑞利波波长;VR为瑞利波的波速;f为频率。
4.2 数据采集方法
传感器收集数据后反馈到计算机进而进行存储。数据采集如图5所示。
如图5所示,数据采集的时间段在2~5 s内,此区段内波形较为稳定。采用此区段的最大加速度值作为一次测试的加速度值,采集过程中连续激振并采集三次,选择三次加速度的平均值以减小误差并作为测试结果。
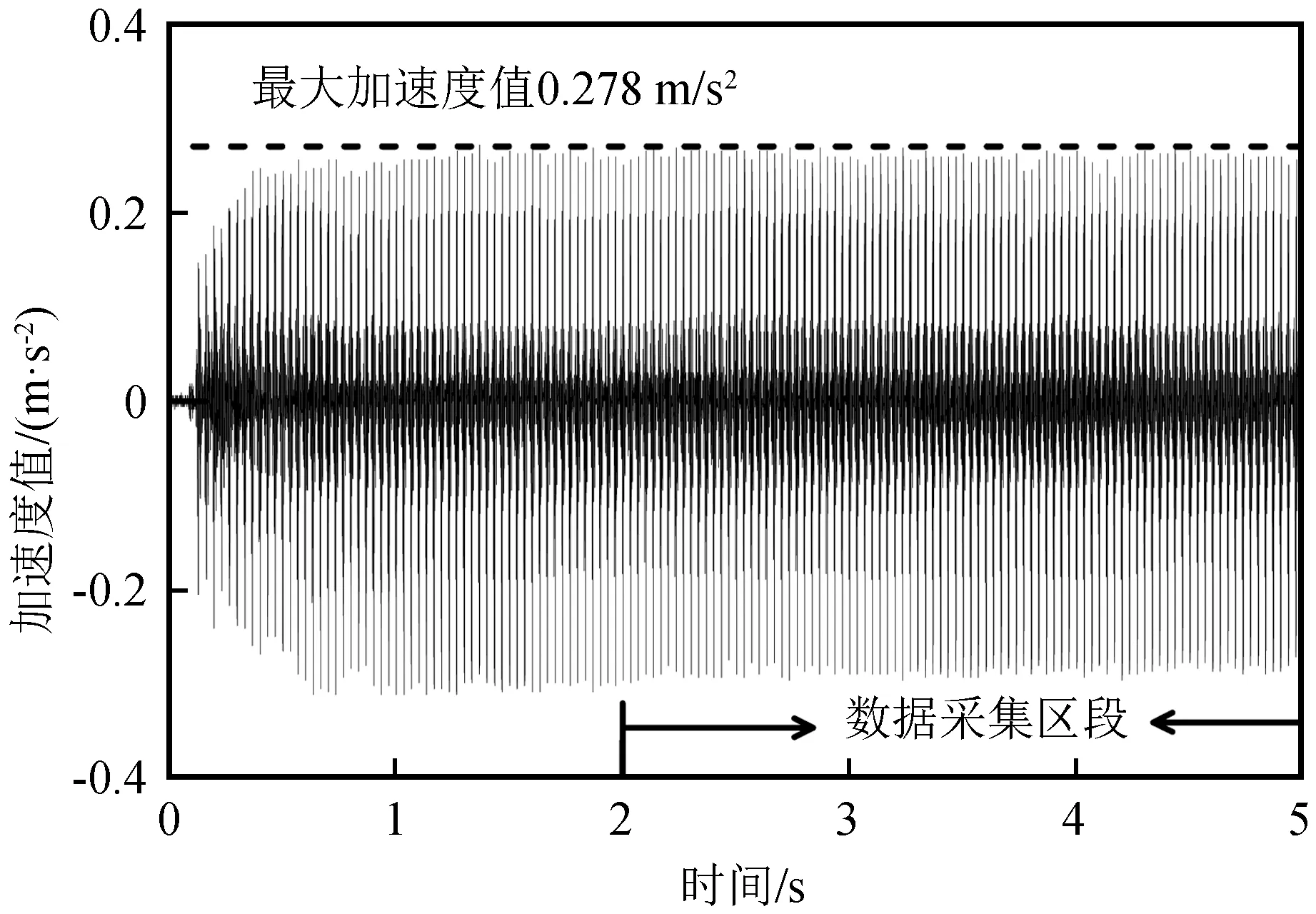
图5 数据采集示意图Fig.5 Schematic diagram of data acquisition
5 几何参数对桩周振动区域的影响
5.1 参数归一化处理
本文将瑞利波波长与单桩尺寸建立联系来分析几何参数变化时单桩振动区域的变化。参数归一化过程如下:
(1)桩长参数L
L=l/LR
式中:l为桩长;LR为瑞利波波长。
(2)桩径参数D
D=d/LR
式中:d为桩径;LR为瑞利波波长。
(3)振源距参数S
S=s/LR
式中:s为振源距;LR为瑞利波波长。
5.2 桩长参数对桩周振动区域的影响
为了研究桩长参数变化时桩周围振动区域的变化,对桩径、振源距控制不变,工况的选取列于表2。

表2 桩长工况安排Table 2 Test arrangement of pile length
通过不同的频率对表2中的工况进行测试,将测试的结果绘制成关于桩长的二维等值线图,测试的结果见图6。本试验条件下,桩长参数L的取值范围在0.109~1.091。

图6 桩长变化下二维等值线图Fig.6 Two-dimensional contour map with different pile length
在图6中,桩前、桩两侧存在着Ar值放大的现象,在桩后则存在Ar值减小的区域。在桩前放大的区域中,当桩长为40 cm时,桩前的Ar值最大在1.3以上,而当桩长为70 cm和100 cm时,桩前放大区域的Ar值达到了1.4以上,且放大的区域集中体现在桩角处,说明桩长的增加会使得桩前放大区域的Ar值有所增加。在桩两侧存在着Ar值在1~1.1的区域,这是由于绕射波所导致的,但其Ar值并未达到1.2以上。在桩后存在着单桩的隔振区域,当桩长为40 cm时,桩后的隔振区域的Ar值最小在0.8以上,其所能达到的隔振效果非常弱,但随着桩长增加到100 cm时,桩后的隔振区域的Ar值达到了0.5~0.6,说明当桩长增加,单桩的隔振效果得到了增强。
徐平[23]以位移比小于0.5的区域为研究对象研究了多排桩对平面弹性波的多重散射问题。由于单桩在桩后很难达到良好的隔振效果,排除试验场地等偶然因素的影响,本文以Ar值小于0.7的区域作为隔振区,用γ来表示,分析桩后的隔振区域的变化。并定义桩前Ar值大于1.1的区域为反射区,用α来表示,桩两边Ar值在1~1.1的区域定义为绕射区,用β来表示。三个变量均以面积的形式进行表示。
由于桩长为40 cm时,单桩桩后隔振区域的Ar值并没在0.7以下,以工况TL-2为例进行区域分划,如图7所示。
在图7中,γ为单桩桩后Ar小于0.7的区域。β的划分范围为线L1与Ar值在1.1~1.2的交汇区域,线L1与桩前侧相重合。α主要为线L1与桩前Ar值大于1.1的交汇区域,本文将桩长参数变化对应的γ、α、β的变化进行拟合,拟合结果如图8所示。

图7 参数区域划分Fig.7 Parameter area division

图8 γ、α、β随L变化图Fig.8 Change of γ,α,β with L
上述各工况拟合方程如表3所列,显著性水平a取0.05。
由表3可知各工况的R值较大且均大于Raf,其拟合方程可较好地反映各变量与L值的关系。

表3 各变量随L值变化的拟合曲线Table 3 Fit curve of each variable with L
如图8所示,随着L的增加,γ的值呈现出增加的趋势,当L值在0.109~0.835的范围内时,随着L的增加,桩后γ区域的面积增长迅速,而当L值增加到0.835~1.022的范围内时,数据增长较为缓慢,趋势趋于平缓。
对于α,当L的值在0.109~0.831范围内时,α值呈现出迅速增长的趋势,而当L值在0.831~0.963的范围内时,桩前反射区的面积增长幅度很小,数据趋于平缓。
对于β值,随着L值的增加,β值呈现出减小的趋势,当L值在0.109~0.840的范围内时,拟合曲线的降低趋势明显,当L值达到0.840~0.962的范围内时,β值变化很小。
综合分析图8,当桩长参数L的值在0.840~0.962的范围内时,隔振区、反射区以及绕射区面积的变化趋于平缓,继续增加桩长对各区域面积影响很小。
5.3 桩径参数对桩周振动区域的影响
桩径是设置排桩隔振的重要变量。在本试验中,同样分析了在桩径变化情况下振动波遇单桩时桩周围土体的振动区域变化情况。在研究单桩桩径这一变量时,对桩长、振源距保持不变,工况安排列于表4,图9为其绘制的二维等值线图。

表4 桩径工况安排Table 4 Test arrangement of Pile diameter
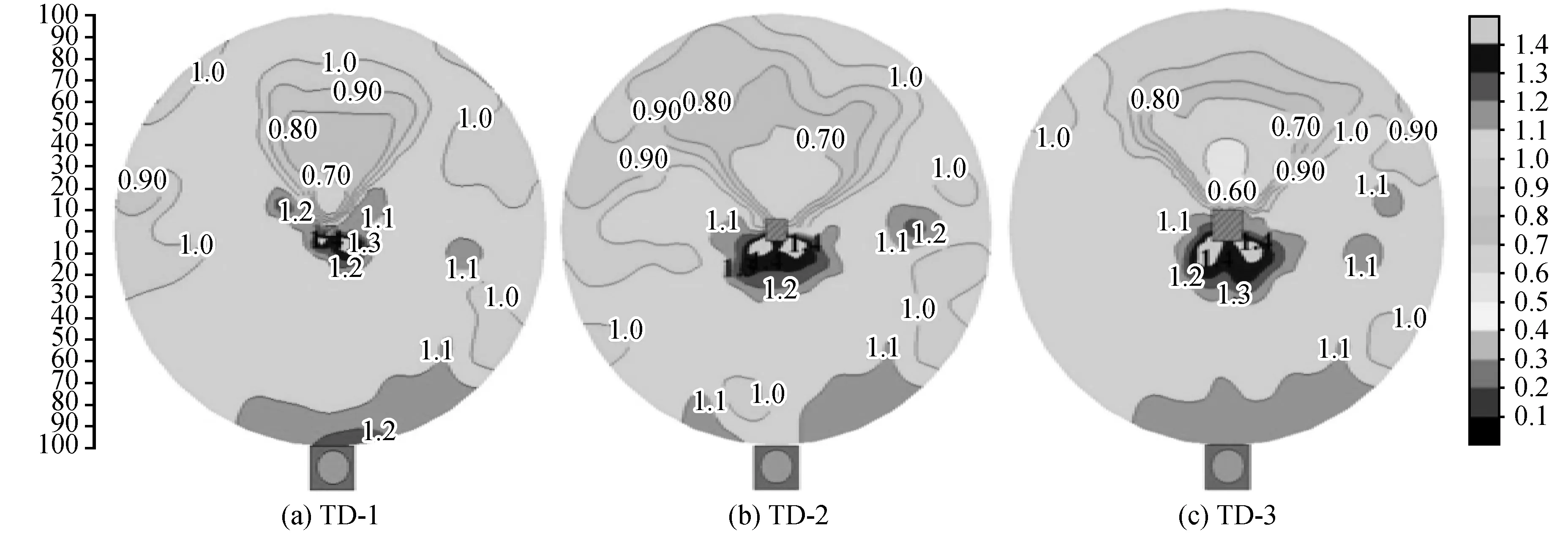
图9 桩径变化下二维等值线图Fig.9 Two-dimensional contour map of pile diameter change
在图9中,桩径的变化对桩周围振动区域的影响较大,具体体现在:桩后隔振区、桩前反射区、桩两侧绕射区的影响。当桩径减小到5 cm时,桩后的隔振区域被限制在了桩后的一段小范围内;当桩径增加到15 cm时,桩后隔振区域的面积明显增大。在反射区域,桩径的改变虽然都使得桩前存在Ar值1.2~1.4的区域,但不同的是区域面积随着桩径的增加而增加。对于桩两侧的绕射区域,在图9中,工况TD-1的绕射区域的面积要明显大于工况TD-3。将桩径参数D与γ、α、β进行拟合,拟合图形见图10。本文中,桩径的取值范围为0.013~0.163。
γ、α、β与桩径参数D拟合方程的相关参数列于表5。
由表5可知各工况的R值较大且均大于Raf,其拟合方程可较好地反映各变量与D值的关系。

表5 各变量随D值变化的拟合曲线Table 5 Fitting curve of each variable with D
由图10可知,桩径参数D对各区域面积的影响较大且并未出现数据的缓和段。随着桩径参数D的增加,γ值从0增加到了0.249 m2,曲线整体趋势较陡,增长速度较快。对于α,拟合曲线整体呈现出上升的趋势,α值从0.029 m2增加到了0.158 m2,增长速度较快。对于β值,随着D值的增加,β呈现出降低的趋势,其值从0.095 m2降低到了0.007 m2,整体降低速度较大,但幅度很小。
综合分析图9、图10,桩径参数在0.013~0.163的范围内增加会使得桩后隔振区、桩前反射区的面积增加明显,但会使得桩两侧绕射区的面积急剧下降。
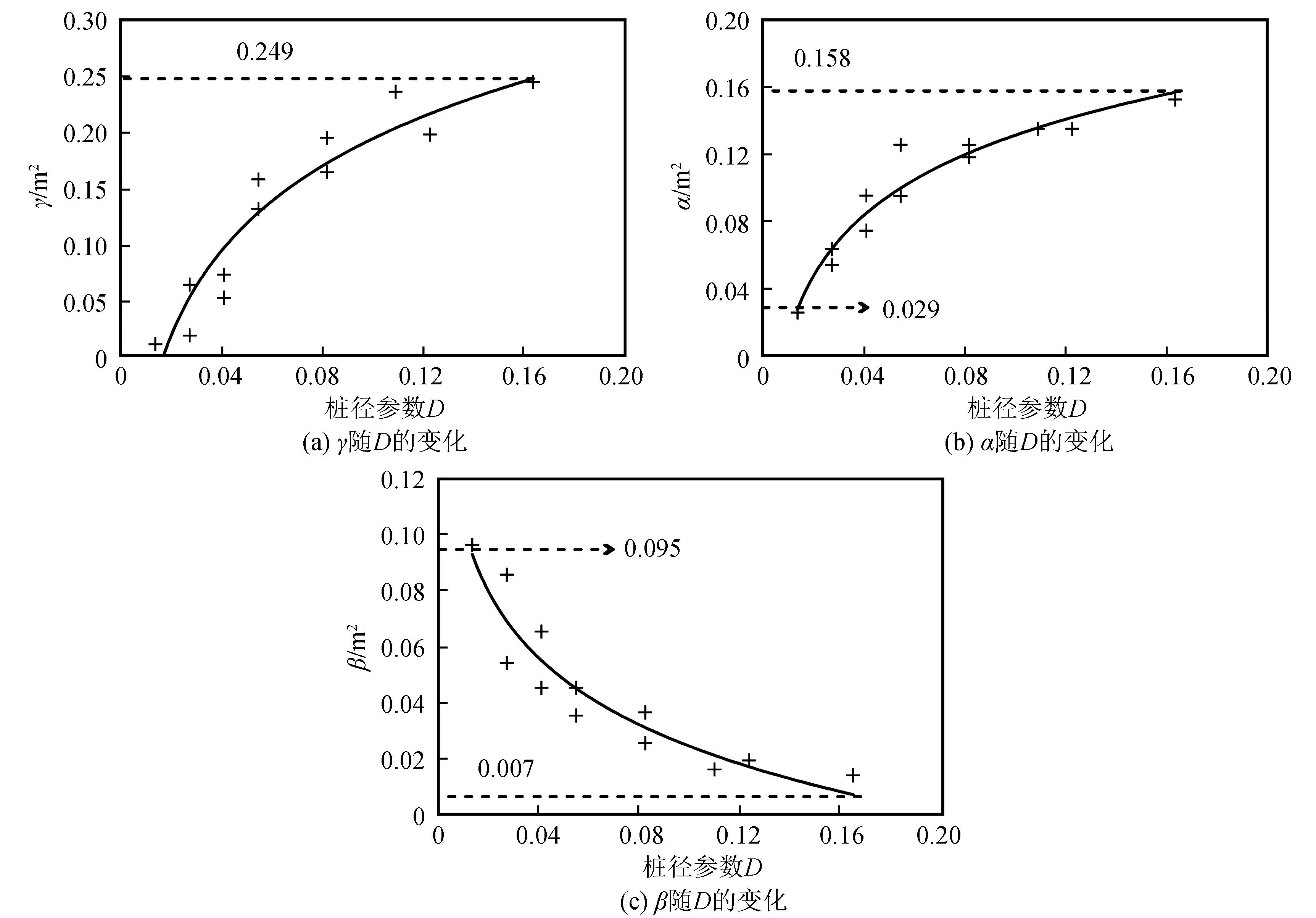
图10 γ、α、β随D变化图Fig.10 γ,α,β with D changes
5.4 振源距参数S对桩周振动区域的影响
为了研究振源距变化时桩周围振动区域的变化,需控制桩长、桩径保持不变。在本试验中,通过改变不同的振源距来表示振源的位置。工况安排列于表6,图11为绘制的二维等线图。

表6 振源距工况安排Table 6 Test arrangement of vibration source distance
从图11中可以看出,当振源距为60 cm、80 cm时,桩前、桩两侧均存在Ar值增大的现象,同样在桩角处Ar值增大更加明显。在桩前的反射区中,两个工况的Ar值在桩前相似,不同的是反射区的面积发生了变化。对于桩后隔振区,当振源距为60 cm时,桩后Ar值在0.5~0.6的区域占据了大部分,同时在区域中间出现了Ar值在0.4~0.5的区域。当振源距增加到80 cm时,隔振区在桩后的面积有所减小,并且Ar值在0.4~0.5的范围消失,最小Ar值的隔振区在0.5~0.6之内。在图11中同时可以看出,振源距从60 cm增加到80 cm时,绕射区的面积发生了明显的变化,当振源距为60 cm时,Ar在1~1.1的区域成块状出现,而当振源距增加到80 cm时,绕射区呈连续状出现。
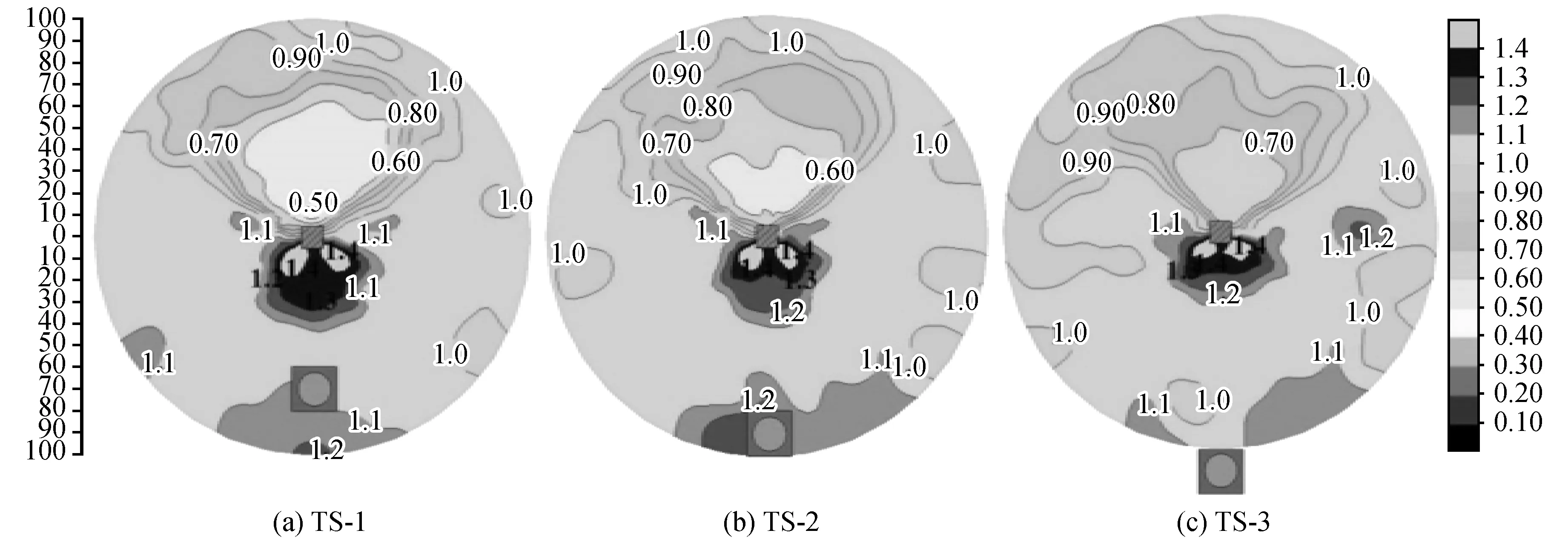
图11 振源距变化下二维等值线图Fig.11 Two-dimensional contour map of different vibration source distance
将隔振区、反射区以及绕射区的面积与振源距参数S值进行拟合,拟合图形见图12,相关拟合图形的拟合方程详见表7,其中显著性水平a取值为0.05。本试验中振源距参数的取值范围为0.163~1.091。

图12 γ、α、β随S变化图Fig.12 Change of γ,α,β with S
表7中各拟合方程的相关系数R均较大且大于临界值Raf,其拟合方程可较好地反映各区域面积变化与参数S的相关性。
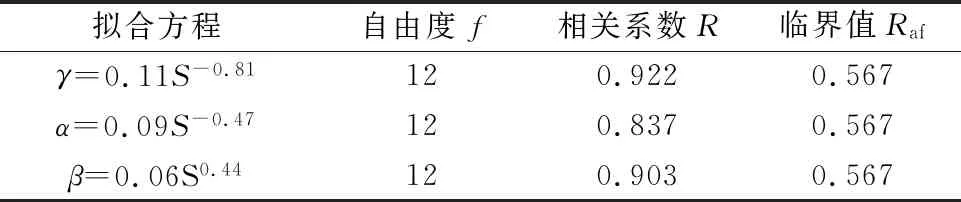
表7 各变量随S值变化的拟合曲线Table 7 Fitting curve of each variable with S
由图12可知,振源距对桩周振动区域的面积影响较大。对于γ,随着S值的增加,γ整体呈现出下降的趋势,当S值在0.163~0.961范围内时,增加S值可使得γ值降低明显,而当S值继续增加到0.961~1.079的范围内时,γ值变化很小,数据出现了缓和段。对于α,S值的增加同样使得α值降低明显,但相比于γ值,α值的降低幅度较小。当S值在0.163~0.923范围内时,α值下降迅速,当S值在0.923~1.068的范围内时,α值虽然仍是降低的趋势,但数据开始缓和,变化幅度很小。对于β值,β与S值几乎成线性增加,但增长幅度很小,数据整体较为缓和,随着S值的增加,β值从0.028增加到了0.065。
综合分析图11、图12,当S值达到0.961~1.068的范围内时,隔振区、反射区的面积变化较小,而绕射区的面积随着S值的增加而增加。
5 结论
本文通过室外试验绘制了二维等值线图,研究了单桩桩长、桩径、振源距、激振频率变化情况下桩前、桩后以及桩两侧振动区域的变化,得出了以下结论:
(1) 桩前、桩两侧存在振动加强区,并且桩两侧的振动区的Ar值要低于桩前的加强区,在桩前加强区中,以桩角处更加突出。
(2) 桩长参数L对隔振区、反射区以及绕射区的面积变化影响较大,当L值在0.109~0.840的范围内时,隔振区、反射区的面积迅速增加,而绕射区的面积减小。当L值在0.840~0.962的范围内时,隔振区、反射区以及绕射区的面积变化很小,拟合曲线趋势趋于平缓。
(3) 桩径参数D对各区域的面积影响较大,随着桩径参数D在0.013~0.163的范围内增加时,隔振区与反射区的面积呈现出较大幅度的增长,分别增长了0.249 m2、0.129 m2,而绕射区的面积降低了0.088 m2,降低幅度较小,但降低的速率较快。
(4) 振源距参数S对单桩周围振动区域的影响较大。当S值在0.163~0.961的范围内时,隔振区与反射区的面积呈现出急速下降的趋势,当S值在0.961~1.068的范围内时,两处面积的变化趋于缓和,但仍在减小。而绕射区的面积几乎随着S值的增加呈现出线性增加的状态,但增加幅度较小,仅仅增加了0.037 m2。

