电网故障下永磁直驱风电机组机电暂态全过程等值建模方法

杨旼才， 余建峰， 欧阳金鑫， 夏翰林， 姚 骏

(1. 国网重庆市电力公司电力科学研究院， 重庆 404100；2. 输配电装备及系统安全与新技术国家重点实验室，重庆大学， 重庆 400044)

1 引言

近年来，风电装机容量持续增长。其中，基于永磁同步发电机(Permanent Magnet Synchronous Generator, PMSG)的永磁直驱风电机组(Permanent Magnet Wind Turbine, PMWT)由于其安全可靠性和运行效率高、无功调节能力强及维护成本低等优点，在风电场中所占的比重越来越高，已成为目前的主流机型[1,2]。但是，随着风电的大量应用，电压波动、系统暂态稳定等问题逐渐暴露[3-5]。特别是全功率背靠背变流器将PMSG与电网隔离，使其二者运行不同步，由此产生了新的暂态稳定问题。因此，亟需建立不同工况和不同状态下的PMWT模型。

PMWT的模型包括详细模型和简化等值模型两类。详细模型完整模拟了风力机、传动轴系、永磁同步发电机、全功率变流器及其控制系统的响应特性。但是，详细模型阶数高、运行速度慢，将其应用于电力系统的分析十分复杂且低效。为此，部分文献通过降低阶数来建立PMWT的简化模型。文献[6]建立了集中质量块传动系统的机组模型用以模拟风电机组对电网的频率影响。文献[7]简化了变流器和变压器。文献[8]提出电励磁同步电机等效PMSG的风电机组建模方法，增加了转子特性的影响。文献[9]基于PMSG能够快速跟踪给定的功率指令的特点，将其等值为可控功率源。文献[10]将PMWT简化为电压源型逆变器等值模型和受控电压源等值模型。文献[11]对传动系统模型与变流器模型进行了降阶简化，同时忽略了桨距角控制模型。文献[12]建立了适用于小干扰稳定分析的PMWT降阶模型。文献[13]将发电机-变流器模型等值为代数运算的可控电流源。但是，上述模型均未考虑在电网故障期间PMWT状态的多样性及其状态的切换过程。

由于电力系统发生故障时，风电机组机侧和网侧功率不平衡，因此机侧多余的功率将对PMWT直流电容进行充电，可能导致直流电容过电压，因此一般需要通过卸荷来消耗不平衡功率[14,15]。现有卸荷方法主要是在直流电容侧加卸荷电路(chopper)。此外，由于电力系统发生故障时PMWT输出电流增大，会损坏变流器，所以需要闭锁变流器。目前通常利用对电力电子器件施加负电压脉冲进行关断，从而实现闭锁。chopper的投入和变流器的闭锁均会改变PMWT的主回路，导致PMWT的输出特性发生变化，因此，PMWT的建模必须考虑卸荷电路(chopper)是否投入以及变流器是否闭锁。但是，针对低电压穿越影响下PMWT的全过程建模，目前仍然鲜有研究。某一状态下的单一模型忽略了PMWT结构改变带来的输出特性变化，势必产生极大偏差。

文中考虑了变流器控制响应特性以及低电压穿越影响，提出了一种PMWT机电故障暂态全过程建模方法。首先建立了PMWT的数学模型；随后分析了电网故障下PMWT的多状态性；提出了考虑PMWT多态性的机电暂态全过程建模思想；并建立了PMWT各种状态的机电暂态等值模型，进而通过推导状态切换条件，建立了PMWT故障全过程的机电暂态等值模型；最后通过仿真验证等值模型的有效性。

2 永磁直驱风电机组数学模型

永磁直驱风电机组由风力机、PMSG、全功率背靠背变流器及控制系统等组成，其结构如图1所示。其中，控制系统主要包括桨距角控制、机侧和网侧变流器控制和低电压穿越控制。在PMWT中，风力机将叶片捕获的风能转化为机械能，驱动与其同轴连接的永磁同步发电机旋转，从而转化为电能输出至电网。PMSG通过具有隔离作用的全功率变流器与电网连接，使发电机的转速摆脱电网频率的约束，实现了变速恒频运行。

图1 PMWT的结构Fig.1 Structure of PMWT

2.1 风力机模型

风力机叶片捕获的风能和叶片扫过的面积、风能利用系数和风速相关，可表示为：

(1)

式中，Pw为风轮面扫过的功率;Cp为风能利用系数；ρ为空气密度;Rw为风轮半径;vw为风速。

2.2 轴系模型

轴系模型的详细模型高达11阶[16]，兼顾轴系特性和简化等值的目标， PMWT的轴系等效为两质量块模型，可表示为：

(2)

式中，Hw、He分别为风力机和发电机转子惯性时间常数；ωw、ωm分别为风力机和发电机转子机械角速度;θs为风力机相对于发电机转子的角位移;Ds为风力机和发电机转子轴阻尼系数;Ks为轴的刚性系数；Tm、Te分别为风轮输入机械转矩和发电机电磁转矩;ω0为电气基准角速度。

2.3 永磁同步机模型

PMSG采用永磁体励磁，没有阻尼绕组。永磁体安装固定在转子上，为发电机提供恒定的励磁磁场。PMSG定子绕组采用电动机惯例,其在两相旋转坐标dq轴下的数学模型为：

(3)

式中，usd、usq分别为定子d、q轴电压；isd、isq分别为定子d、q轴电流；Rs为定子绕组电阻；Ld、Lq分别为定子绕组d、q轴同步电感；p为发电机极对数；ψf为发电机中永磁体的磁链幅值。

PMSG输出的有功功率和无功功率为：

(4)

2.4 机侧变流器控制系统

全功率背靠背变流器控制系统是PMWT控制系统的核心。机侧变流器一般采用零d轴电流控制，使电磁转矩仅与定子q轴电流相关，从而实现有功、无功功率的解耦控制。机侧变流器控制系统采用功率外环、电流内环的结构。功率外环控制方程为：

(5)

电流内环的控制方程为：

(6)

式中，ωe为发电机电角速度；kpsc、kisc为电流内环的PI系数。

2.5 网侧变流器控制系统

网侧变流器采用电网电压定向矢量控制以实现有功和无功的解耦控制。电网正常运行期间无功功率参考值一般设置为零，从而保证PMWT单位功率因数运行。网侧变流器控制系统一般采用电压外环、电流内环的控制方式。电压外环控制方程为：

(7)

电流内环的控制方程为：

(8)

式中，ugd、ugq分别为网侧变流器端d、q轴电压；igd、igq分别为网侧d、q轴电流；egd、egq分别为网侧d、q轴电压；Lg为网侧进线滤波电感；kpgc、kigc为电流内环的PI系数。

2.6 桨距角控制模型

桨距角控制是根据风速的大小调整桨矩角，保证风力机稳定运行在额定转速和转矩下，确保输出功率稳定。桨距角控制模型采用转速控制的PI调节器：

(9)

式中，β为桨距角；ωe、ωe_ref分别为发电机转速的实时值和参考值；kpω、kiω为PI系数。

3 全过程机电暂态建模思想

3.1 PMWT的故障多态性

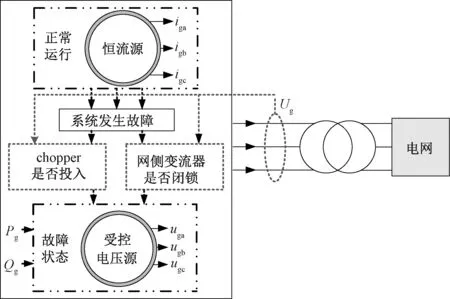
为了避免机网侧功率不平衡导致直流电压的突变，PMWT会根据故障程度投切卸荷电路以维持直流电压稳定。卸荷电路的投切常采用滞环比较逻辑[17]，如图2(a)所示，当直流电压udc>udcmax时，投入卸荷电路；当直流电压udc

为了避免机端电压跌落导致网侧过流损坏变流器，故障严重时触发网侧变流器闭锁动作。变流器闭锁判据采用网侧输出电流Ig电流值[18]，如图2(b)所示，当Ig大于变流器电流限幅值Imax时，变流器闭锁，反之变流器正常运行。

图2 卸荷电路投切与变流器闭锁逻辑Fig.2 Unloading circuit switching and converter blocking logic

当电压跌落程度较小时，此时直流侧电压未超过保护阈值，chopper不投入，PMWT运行于未投chopper状态。当电压跌落程度较大时，chopper投入以消耗机网侧不平衡功率，限制直流侧电压增大，此时PMWT运行于带chopper状态。PMWT还存在网侧变流器闭锁以及未闭锁2种运行状态。由于故障程度的不同导致电压跌落程度不同，而且chopper是否投入与网侧变流器是否闭锁都与电压相关，所以，PMWT存在5种运行状态：正常状态、未投chopper状态、带chopper状态、网侧变流器未闭锁状态和网侧变流器闭锁状态。

PMWT的多状态特性如图3所示，运行于正常状态(模式0)的PMWT遭遇电网故障，导致机端电压跌落。此时chopper投切判据启动，当电压跌落程度较小时，风电机组运行于未投chopper状态，同时判断网侧变流器是否闭锁，当网侧变流器未闭锁时，PMWT运行于未投chopper状态下网侧变流器未闭锁状态(模式1)，当网侧变流器闭锁时，PMWT运行于未投chopper状态下网侧变流器闭锁状态(模式2)。当电压跌落程度较大时，风电机组运行于带chopper状态，当网侧变流器处于未闭锁状态时，PMWT运行于带chopper状态下网侧变流器未闭锁状态(模式3)，当网侧变流器处于闭锁状态时，PMWT运行于带chopper状态下网侧变流器闭锁状态(模式4)。

图3 PMWT的多状态特性Fig.3 Multi-state characteristics of PMWT

PMWT风电机组呈现出故障多态性的特点，并且在电网故障下存在5种模式的切换。chopper的投切判据常采用直流电压，网侧变流器闭锁判据常采用网侧变流器电流，为实现各模式下等值模型的切换，需采用统一的判据，由于等值模型中不存在直流电压，因此采用PMWT机端电压作为chopper投切和网侧变流器闭锁判据。

3.2 PMWT的等值建模原理

在电力系统暂态特性分析时，风电机组详细模型计算复杂，无法满足系统的计算步长要求，而且系统故障期间主要关注风电机组的外特性[19]，因此需要对PMWT进行相应的简化。文中比较PMWT各状态量的时间常数与电力系统机电暂态分析的时间尺度的关系，进而对PMWT进行简化等值建模。

根据时间常数的定义，感性元件时间常数为τ=L/R,容性元件时间常数为τ=RC。根据PMWT小信号模型计算状态矩阵的特征值，并定义特征值的倒数为该变量的时间常数[20]，可得到机侧和网侧变流器电流的时间常数。PMWT主要时间常数如表1所示，PMWT参数见表2和表3。

表 1 PMWT主要时间常数Tab.1 Main time constant of PMWT

表2 PMWT主要参数(2 MW)Tab.2 Main paramoter of PMWT(2 MW)

表3 控制器参数Tab.3 Parameter of Controller

含PMWT的电力系统机电暂态稳定的时间尺度为100 ms级，对时间常数小于机电时间尺度的变量(一般小于1/4以上)，认为在机电暂态分析时已由动态进入稳态，其微分方程由代数方程表示。对于时间常数远大于机电时间尺度的变量态(一般大于4倍以上)，认为其保持不变，微分方程由常量表示。结合表1风电机组各状态量的时间常数可以看出，在PMWT机电暂态建模时可近似直流电压、机侧和网侧变流器电流进入稳态，用代数方程建模。网侧滤波器电流保持不变，用常量表示。

4 故障全过程机电暂态等值模型

4.1 模式0下的等值模型

由于风机对风速波动体现为低通滤波特性，且滤波时间常数较大，约为10 s级[16]，所以在机电暂态分析中风速可视为恒定。PMWT在电网故障发生前的稳态过程中输出恒定的功率，同时电网电压为恒定值，因而PMWT的输出电流也保持恒定值。PMWT输出电流Ig的表达式为：

(10)

由式(10)可知，电流Ig为恒定值，因此PMWT在电网正常运行状态下可等值为恒流源。

4.2 模式1下的等值模型

由于电流内环的时间尺度远小于外环机电时间尺度，且内环响应速度更快，因此变流器输出至电网的电流近似等于外环参考值。网侧变流器的时间尺度为10 ms级，在电力系统机电暂态稳定时间尺度内PI能跟踪上其暂态过程，同时由于积分控制的响应速度不及比例控制，因此机电暂态建模时忽略PI控制器积分环节，则根据式(7)，可得：

(11)

直流电压表达式为：

(12)

式中，C为直流电容值。

模式1下网侧d、q轴电流值为：

(13)

式中，igd_tim、igq_tim分别为网侧d、q轴电流实时值。

联立式(11)～式(13)，PMWT的复功率可写为：

(14)

所以，机端电压Ug可写为：

(15)

由式(15)可见，机端电压受控于功率参考值及网侧输出电流，因此模式1下的PMWT可等值为受控电压源。

4.3 模式2下的等值模型

模式2下chopper未投入，但是网侧变流器输出电流已达到变流器电流限幅值，导致网侧变流器闭锁。根据风电机组并网导则无功要求确定igq，由网侧d、q轴电流和变流器电流限幅值的关系可得到网侧d轴电流[21]：

(16)

式中，UT为并网点电压标幺值；IN为发电机额定电流幅值；Imax为网侧变流器电流限幅值。

联立式(11)、式(12)和式(16)，PMWT的机端电压可写为：

(17)

由式(17)可见，模式2下的PMWT可等值为受控电压源，和模式1等值模型的区别在于复功率的参考值不同。

4.4 模式3下的等值模型

模式3下chopper已投入，但是网侧输出电流小于变流器电流限幅值，因此网侧变流器处于未闭锁状态。相较于未投chopper状态，投入chopper电路后，PMWT机电暂态特性的分析需考虑卸荷电路对直流电压的影响。

带chopper的PMWT中直流电压表达式为：

(18)

式中，Rch为卸荷电路电阻值。

联立式(11)、式(13)和式(18)，PMWT的机端电压可写为：

(19)

由式(19)可见，模式3下的模型仍可等值为受控电压源，和模式1等值模型相比，有功功率部分减去了卸荷电路的消耗功率。

4.5 模式4下的等值模型

在模式4下，chopper已投入，网侧变流器运行于闭锁状态。由式(11)、式(16)和式(18)，PMWT的机端电压可写为：

(20)

由式(20)可知，模式4下的PMWT可等值为受控电压源。和模式3等值模型相比，复功率中网侧限流值不同。综合PMWT正常运行等值模型、chopper是否投切和网侧变流器是否闭锁下的5种等值模型，PMWT全过程机电暂态等值模型如图4所示。当PMWT处于正常运行阶段时，PMWT的等值模型为恒流源模型，输出的三相对称电流经升压变流入电网。当电网发生故障时，通过机端电压Ug判断chopper是否投入和网侧变流器是否闭锁，将PMWT等值为基于不同功率参考值的受控电压源。因此，PMWT的全过程机电暂态等值模型包括正常运行阶段的恒流源模型和故障切换后的等值受控电压源模型。

图4 PMWT全过程机电暂态等值模型Fig.4 Full- process electromechanical transient equivalent model of PMWT

5 全过程机电暂态等值模型的切换

5.1 基于机端电压的chopper投切判据

在同步旋转dq坐标下，网侧变流器采用电压定向矢量控制，将机端电压矢量U定向在d轴上，有ugq=0。则网侧有功功率方程可写为：

Pg=1.5Ugigd

(21)

式中，Ug为机端电压。

机电暂态研究的时间尺度为100 ms级以上，可近似网侧变流器PI能跟踪上其暂态过程，根据式(8)，网侧内环控制方程可写为：

(22)

根据式(12)、式(21)和式(22)，可得chopper投切判据：

(23)

图5 chopper投切逻辑流程图Fig.5 Flow chart of chopper switching logic

5.2 基于机端电压的网侧变流器闭锁判据

根据电压矢量定向原则，ugq=0，由网侧变流器输出的复功率、电压和电流的关系可得：

(24)

式中，Ig为网侧电流的共轭值。

根据网侧变流器电流限幅值与电网电流的闭锁判据，当Ig>Imax时，网侧变流器闭锁。根据式(24)可得基于机端电压的网侧变流器闭锁判据：

(25)

当满足上述判据时，网侧变流器闭锁；否则网侧变流器处于正常运行模式。

6 算例分析

6.1 模式1下的等值模型

0.5 s时电网发生三相短路故障，风电机组机端电压跌落至0.9 pu。电压跌落程度较小时，根据切换条件可知chopper未投入，网侧变流器未闭锁。全过程机电暂态模型根据机端电压判断采用模式1的等值模型进行计算。PMWT的详细模型和全过程机电暂态模型的输出特性如图6所示。其中，虚线为详细模型的输出，实线为全过程机电暂态模型的输出。

图6 三相对称故障下电压跌落至0.9 pu特性对比Fig.6 Comparison of characteristics of voltage drop to 0.9 pu under three-phase symmetry fault

图6中，故障发生时刻，PMWT的有功输出和电压发生跌落，根据电网导则无功要求，故障期间PMWT的无功输出有所增加。详细模型和全过程机电暂态模型的有功、无功、电压、电流输出特性基本一致。等值模型有功的误差不超过0.5%，无功误差不超过0.5%，电压误差不超过1%，电流误差不超过5%。产生误差的主要原因是等值模型只考虑了变流器的线性特性，忽略了调节延时、过调制等非线性因素。全过程机电暂态模型的误差均在允许范围内，能够准确模拟机组的输出特性。

6.2 模式3下的等值模型

0.5 s时电网发生三相短路故障，风电机组机端电压跌落至0.5 pu。此时，电压跌落程度较大， chopper投入，网侧变流器未闭锁。全过程机电暂态模型根据机端电压判断采用模式3的等值模型进行计算。PMWT的详细模型和全过程机电暂态模型的输出特性如图7所示。

图7 三相对称故障下电压跌落至0.5 pu特性对比Fig.7 Comparison of characteristics of voltage drop to 0.5 pu under three-phase symmetry fault

由图7可知，详细模型和机电暂态等值模型的有功、无功、电压、电流输出特性基本一致。等值模型有功的误差不超过0.3%，无功误差不超过0.3%，电压误差不超过1%，电流误差不超过5%。在故障开始时刻，输出特性有部分差异，主要原因是故障发生瞬间电压跌落较大，触发卸荷电路的投入，对风电机组的输出影响较大，电压、电流产生了一部分超调量，进而导致功率在该时刻的突变。

6.3 模式4下的等值模型

0.5 s时电网发生三相短路故障，风电机组机端电压跌落至0.3 pu。此时chopper投入且网侧变流器闭锁。全过程机电暂态模型根据机端电压判断采用模式4的等值模型进行计算。PMWT的详细模型和全过程机电暂态模型的输出特性如图8所示。

图8 三相对称故障下电压跌落至0.3 pu特性对比Fig.8 Comparison of characteristics of voltage drop to 0.3 pu under three-phase symmetry fault

由图8可知，详细模型和全过程机电暂态模型的有功、无功、电压、电流输出特性基本一致。等值模型有功的误差不超过0.5%，无功误差不超过1.5%，电压误差不超过1%，电流误差不超过5%。与模式3类似，在电压跌落程度较大的情形下，网侧输出有功的跌落程度更大，因此所需要的无功支撑也就越大，此时卸荷电路投入和变流器闭锁，对风电机组的输出影响增大，进而误差增大。但是，误差仍然位于允许范围内，全过程机电暂态模型能够准确模拟机组的输出特性。

6.4 模式2下的等值模型

改变网侧电流的限幅值为Imax=1.1IN。0.5 s时电网发生三相短路故障，风电机组机端电压跌落至0.7 pu。此时，chopper未投入，网侧变流器闭锁。全过程机电暂态模型根据机端电压判断采用模式2的等值模型进行计算。PMWT的详细模型和全过程机电暂态模型的输出特性如图9所示。

图9 三相对称故障下电压跌落至0.7 pu特性对比Fig.9 Comparison of characteristics of voltage drop to 0.7 pu under three-phase symmetry fault

由图9可知，故障发生时刻，PMWT的有功和无功输出较模式1出现了部分振荡。故障期间PMWT的有功输出减小，无功输出有所增加。详细模型和全过程机电暂态模型的有功、无功、电压、电流输出特性同样基本一致。等值模型有功的误差不超过2%，无功误差不超过0.5%，电压误差不超过1%，电流误差不超过5%，此时的误差来源主要是变流器的特性影响。全过程机电暂态模型的误差均在允许范围内，能够准确模拟机组的输出特性。

6.5 不同模式下等值模型的切换

图10 不同模式下等值模型的切换Fig.10 Switching of equivalent models in different modes

由图10(b)可知，网侧电压在0.5 s时跌落至0.5 pu，此时风电机组运行于模式3，在0.8 s时电压进一步跌落至0.3 pu，由判据式(25)可知网侧变流器闭锁，风电机组进入模式4，模式3到模式4的切换验证了网侧变流器闭锁判据的正确性。网侧电流输出波形与判据得到的结果一致。同时等值模型切换后的网侧电压、电流与对应模型的输出特性基本一致，进而验证了不同模式下等值模型的正确性。

7 结论

针对PMWT机电暂态特性难以准确模拟的问题，文中考虑了变流器控制响应特性以及低电压穿越影响下PMWT的故障多状态性，提出了PMWT的机电暂态全过程建模思想，建立了PMWT各个状态下基于不同功率参考值的等值模型，并推导了基于PMWT机端电压的chopper投切和网侧变流器闭锁判据，建立了PMWT全过程机电暂态等值模型。最后通过仿真对比了PMWT详细模型和全过程机电暂态模型各状态下的输出特性，验证了全过程机电暂态模型应用于电力系统暂态稳定分析的准确性，对提高含PMSG的电力系统分析计算效率和风电场接入系统的稳定分析计算具有一定的指导意义。