基于小波能量熵的配电网电压暂降源定位方法

胡安平， 姜玉洁， 陶以彬， 孙浩天， 易 皓

(1. 江苏省储能变流及应用工程技术研究中心(中国电力科学研究院有限公司)， 江苏 南京 210003；2. 西安交通大学电气工程学院，陕西 西安 710049)

1 引言

随着电气化程度的提高，特别是敏感性用电设备的大量使用，对电能质量的要求也越来越高。其中，电压暂降问题是用户投诉比重最多的问题，也是影响设备运行的主要原因。在引起电压暂降的诸多因素中，短路故障是导致电压暂降的主要原因。根据监测系统的信息，对引起电压暂降的短路故障源进行定位，有助于供用电双方区分暂降责任，也对维护电网的安全稳定运行具有重要意义[1-3]。

针对电压暂降源定位问题，国内外学者展开了大量的研究。从定位精度的角度可分为上下游定位、区段定位、精确定位。

第一类为传统的上下游定位，依据单个监测点信息判断故障发生在监测点的上游还是下游。文献[4]将已有的上下游定位方法分为五类：基于扰动能量与扰动功率、 基于电流变化、基于阻抗变化、基于电压测量值、基于电流测量值。此类方法得到的故障区域大，主要依赖人工巡线进一步确定故障位置。

第二类方法为基于馈线终端单元(Feed Terminal Unit，FTU)的故障区段定位，包括矩阵算法与人工智能算法。文献[5]提出改进矩阵算法，根据配电网结构特点构造网络关系矩阵，结合FTU上传的过电流信息，生成故障诊断矩阵，依据故障评价函数确定故障区段。矩阵算法[6]及其改进算法原理简单，但容错性较差。人工智能算法的主要思路为对FTU上报的过电流信息进行编码，构造评价函数，利用智能算法求解，实现故障定位。文献[7]提出基于遗传算法的故障定位方法，在故障信息出现畸变时，能自动纠错，具有高容错性能，但求解时容易陷入局部最优。文献[8]对各馈线区段故障状态进行二进制编码，引入二进制粒子群算法，适用于单电源辐射状配电网故障定位。文献[9]针对分布式电源接入对配网故障定位的影响，构建了新的开关函数，引入多种群遗传算法以解决遗传算法的早熟收敛问题，提高了收敛效率，具有一定的有效性与容错性。

第三类方法为精确定位，即确定故障的具体发生位置，定位精度最高。文献[10]利用变电站捕获的电压和电流来求解复功率方程以进行定位；文献[11]利用压缩感知技术识别故障节点。另外，基于高频瞬变的方法通常通过行波的传播时间来求解故障位置[12]。然而，此类方法往往需要电能质量监测装置具有较高的采样频率及同步精度，因而其实施成本往往较高。除此之外，近年来兴起的大数据和机器学习技术也逐渐被应用于故障定位问题上。文献[13，14]探索了利用数据挖掘和聚类求解配网故障定位问题的可行性。这些方法通常对各种网络拓扑具有良好的适应性，但同时也大大增加了求解故障位置的计算成本。

上述文献中的故障定位方法需要进行电压、电流的测量。然而，故障发生时，故障电流激增，易造成测量误差。随着电流量测量误差的增大，相应方法的故障定位误差也会随之增大。因此，有必要提出一种仅使用电压进行故障定位的方法。

为实现上述提到的各功能，本研究提出了一种基于小波能量熵的新型故障定位算法。由于各节点距离故障位置远近不同，节点电压会发生不同程度的突变，利用小波能量熵对突变信号敏感的特点，根据测量得到的电压量计算各节点的小波熵。不同于以往将小波能量熵应用于故障检测，本研究创造性地提出了利用小波能量熵进行暂降定位。小波能量熵取得极大值的节点即为离故障点最近的节点，从而缩小故障范围实现了故障定位，同时避免了电流数据的测量。

2 电压暂降概述

电压暂降是指供电电压方均根值突然降低至额定值的90%～10%，并短暂持续10 ms～1 min后恢复正常的现象[15]。线路故障类型包括四类：三相接地故障、两相接地故障、相间故障和单相接地故障。短路故障发生时，系统电流升高，短路点附近电压降低，电压暂降发生，系统等效模型如图1所示。

图1 电压暂降系统等效模型Fig.1 Equivalent model of voltage sag system

忽略负荷电流，并假设电源为无限大容量电源，即E=1pu，则故障引起的公共点母线PCC电压幅值为：

(1)

式中，ZF为故障点与母线PCC之间的线路阻抗；ZS为母线PCC点与电源之间的系统阻抗。

令ZF=zl，l为故障点与母线之间的距离，z为单位长度线路阻抗，则：

(2)

从式(2)中可以看出，故障点到母线距离越近，暂降程度越大。此外，当系统出现高阻接地短路故障，各节点电压差异不明显，暂降信号微弱导致识别困难。

3 暂降定位方法

3.1 小波能量熵理论

小波变换利用正交小波基将信号分解为不同尺度下的各个分量，即用由小波母函数经过伸缩和平移形成的一系列小波基函数拟合原始信号。任意函数f(t)∈L2(R)的离散小波变换为：

(3)

式中，ψ(t)为小波母函数；j为分解尺度。

经过离散小波变换，得到各分解尺度下的小波系数Cj(k)。这些小波系数表征了不同尺度下局部能量的直观估计。

根据小波变换理论，当小波基函数是一组正交基函数时，变换具有能量守恒的性质，因此，定义单一尺度下的小波能量为该尺度下小波系数的平方和[16]。

(4)

信号总能量为各频带分量能量之和，因此，系统总能量表达式为：

(5)

定义相对小波能量为：

pj=Ej/Etot

(6)

相对小波能量pj反映了某一段信号的能量强度比例，可视作信息论中信号的概率。结合信息熵理论，定义小波能量熵WEE为[17]：

(7)

小波能量熵结合了小波变换多分辨率分析局部特性好的优点与信息熵表征系统复杂度的特性，准确地对信号完成特征提取[18]。小波能量熵熵值越大，信号分布越无序，反之亦然。具体计算流程如图2所示。

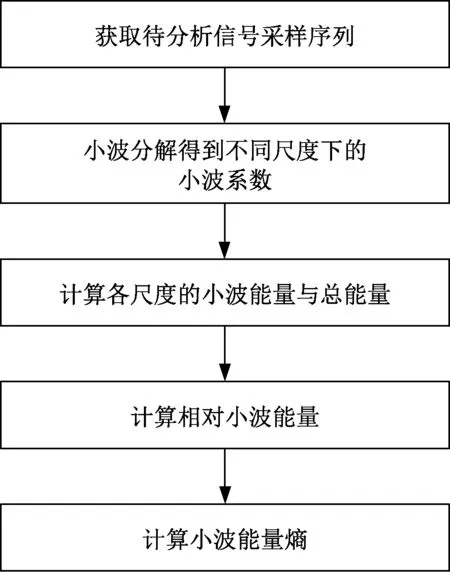
图2 小波能量熵计算流程Fig.2 Calculation process of wavelet energy entropy

从信号的角度来看，出现电压暂降就是在统计特性平稳有序的正常信号中混杂了不一致的异常信号，因此，系统小波能量熵熵值会变大。在以往的研究工作中，根据这一特点，将小波能量熵用于故障检测[17]。而本研究则考虑到各节点的电压暂降程度与距离相关，距离故障点越近，其暂降程度越深。因此，在暂降源节点处，小波能量熵具有极大值，利用小波能量熵可以确定离电压暂降源远近的相对位置，实现故障定位。

3.2 软阈值去噪

由于信号采集过程中难免会产生噪声，噪声信号对小波变换的各个分支都有影响，进而会对小波熵算法产生一定影响[18]，故采用小波去噪对采集到的电压信号进行降噪处理。噪声的小波变换系数主要分布在小尺度上，而信号的小波系数一般不随尺度变化。根据噪声与信号在不同频带上的小波分解系数具有不同强度分布的特点，将各频带上的噪声对应的小波系数去除，保留原始信号的小波分解系数，然后对处理后的系数进行小波重构，得到纯净信号。本研究采用软阈值去噪方法，具体步骤如图3所示。

图3 软阈值去噪流程图Fig.3 Flow chart of soft threshold denoising

其中，阈值函数如式(8)所示，ωλ为阈值处理得到的新的小波系数。当小波系数ω的绝对值小于给定阈值λ时，令其为0；大于阈值时，令其减去阈值λ。

(8)

阈值选择为：

(9)

式中，λ为信号的长度；将小尺度上的小波分解系数进行标准差估计并定义为s，s=M/0.674 5；M为一尺度分解得到的小波系数的中值；n为信号的长度。

3.3 暂降定位流程

综上所述，暂降源定位具体流程如图4所示。实时采集各电能质量监测点电压信息，对采集到的电压信息进行预处理，包括小波软阈值去噪和电压有效值计算。接着，根据电压有效值计算暂降深度，判断是否发生电压暂降，若没有发生电压暂降，继续采集电压数据进行判断；若发生电压暂降，根据暂降深度确定故障相。对故障相进行小波分解，并计算各节点小波能量熵。最后，输出小波能量熵极大值的节点，即为故障点。

图4 暂降源定位流程图Fig.4 Flow chart of sag source location

4 算例验证

为验证所提暂降定位算法的有效性，本研究分别对IEEE14节点模型和IEEE33节点模型进行修改，模拟了三相接地故障、两相接地故障、相间故障和单相接地故障四种短路故障，分别经过阻值为0.1 Ω、10 Ω的故障过渡阻抗。IEEE14节点系统接线如图5所示，IEEE33节点系统接线图如图6所示。Daubechies系列小波正交、紧支，对不规则信号较为敏感，所以本研究选用db4小波进行小波变换。另外，在电压测量中额外加入均值为0且标准差为σ的复数高斯噪声，以便测试该算法的去噪能力。基于Matlab/Simulink实现了所提出的故障定位方法，并在同一平台进行了测试结果的数据统计处理。

图5 IEEE14节点仿真模型Fig.5 Simulation model of 14-node distribution system

图6 IEEE33节点仿真模型Fig.6 Simulation model of 33-node distribution system

4.1 正确性验证

首先在IEEE14节点模型上进行测试，依次在14个节点上放置故障模块模拟四种短路故障，故障过渡电阻RF=0.1 Ω，按照图4所示步骤，记录全部14个节点各次故障时的小波能量熵。为了便于分析，将结果用灰度图的形式表示，并构成14×14的方格图，方格(x,j)表示x节点发生故障时，j节点的小波能量熵，方格颜色越深，表明数值越小，反之，方格颜色越浅表明数值越大。下文中的灰度图中的方格均为相同含义。

仿真结果如图7所示，四种故障仿真结果均为对角线元素为白色，与周围节点呈现黑色色块明显分开，由理论分析可知，如果方格图上对角线元素越明显，说明小波能量熵能较好地表征暂降源位置，从而验证了本方法的正确性。针对图7上对角线之外的白色色块，结合IEEE14节点模型，可知这些节点离故障节点的电气距离比较近，所以小波能量熵比较大，因而该区域呈现白色，但仍小于故障节点的小波能量熵，仍可以区分出故障节点。

图7 IEEE14节点模型小波能量熵(RF =0.1 Ω)Fig.7 Wavelet energy entropy in 14-node distribution system (RF =0.1 Ω)

在IEEE33节点系统模拟了三相短路故障，进行暂降定位算法的测试，由于IEEE33节点系统属于辐射状配电网络，只有一个中心电源，线路末端受暂降影响更深，此时若根据电压信号的大小判断电压暂降源，很显然，暂降源均定位在线路末端。按所提的小波能量熵暂降定位方法进行测试，仿真结果如图8所示，以对角线为分界线，上下游节点明显区分开来，故障上游节点为深色，下游为浅色。这是因为上游节点有电源电压支撑，几乎不受下游暂降的影响，而下游节点没有电源电压支撑，受暂降影响较深。这可以解释图8第1行全为浅色的原因，节点1发生短路故障后，电源与下游节点断开，所有节点均将受到影响。根据小波能量熵最大值进行暂降源的定位，仅在节点1，6，10处定位错误，且结果均指向线路末端，定位准确率为90.9%。

图8 IEEE33节点模型小波能量熵(RF=0.1 Ω)Fig.8 Wavelet energy entropy in 33-node distribution system (RF =0.1 Ω)

4.2 故障过渡电阻值的影响

随着故障过渡电阻值的提高，电压暂降程度变浅，以单相接地故障为例，如图9所示，灰度图几乎没有分界线，说明发生高阻故障时，故障节点以及其他节点的电压并没有发生明显变化，故障节点无法同其他节点区分开，此时不能根据电压信号的大小判断电压暂降源。基于小波能量熵进行电压暂降源定位的结果如图10所示，对角线元素为白色，其他位置大多为深色，根据上文分析，这表明根据小波能量熵可以将故障节点与大部分未发生故障的节点区分开，但也存在部分节点判断错误的情况，这可能是由配电网结构复杂、分支众多造成的。

图9 IEEE14节点模型单相接地故障电压值(RF =10 Ω)Fig.9 Voltage value of single-phase faults in 14-node distribution system (RF =10 Ω)

图10 IEEE14节点模型小波能量熵(RF =10 Ω)Fig.10 Wavelet energy entropy in 14-node distribution system (RF =10 Ω)

5 结论

电压暂降对用电设备的安全可靠运行具有重要影响，准确的暂降定位对提高电能质量具有重要意义。本研究提出了一种基于小波能量熵进行暂降定位的方法，确定小波能量熵取得极大值的节点即为离暂降源最近的节点。所提出的暂降定位方法仅需要电压信息，降低了测量误差的影响。同时，对高阻故障引起的电压暂降也表现出较好的定位能力。