TC17钛合金线性摩擦焊接叶片单元件焊缝设计

余学冉， 陈云永

(中国航发商用航空发动机有限责任公司, 上海 200241)

0 前言

钛合金整体叶盘在现代航空发动机中获得了广泛的应用[1]。由于线性摩擦焊接技术可以实现非轴对称复杂截面及异质材料的固相连接，有效避免熔焊中易出现的偏析、裂纹、气孔等缺陷，成为目前国际公认的理想的航空发动机整体叶盘焊接制造与维修关键技术，在MTU和Rolls-Royce等公司的领先推动下，线性摩擦焊接制造技术从2000年之后逐步成功应用于不同型号航空发动机整体叶盘制造[2-4]。

TC17钛合金具有强度高、断裂韧度好，淬透性高和锻造温度范围宽等一系列优点[3]，在Leap和GE90等多个型号的高压压气机中得到了广泛应用。目前国内已经针对TC17钛合金线性摩擦焊接接头组织与力学性能以及焊后热处理制度对力学性能的影响进行了一定研究[5-8]。李祚军等人[9]针对线性摩擦焊接制造的TC11和TC17异质叶片单元件进行了分析和试验，由于不同焊缝位置处的叶片振动应力的差异及焊缝位置变化对叶片单元件的振动应力梯度产生的影响，焊缝位置对于叶片的疲劳寿命有显著影响。

整体叶盘在使用过程中，除了受到气动力、温度和离心力等随转速变化的稳态应力外，由于其薄壁结构的特点，还容易受到气流激振而产生交变的振动应力[10]。在评估叶片高周疲劳性能时，往往通过Goodman图来综合考虑稳态应力和交变应力的影响[11]。根据文献[6-7]研究结果，热处理前，TC17线性摩擦焊接头的抗拉强度差异约为母材的91.8%左右，高周疲劳性能约为热处理后疲劳性能的83%左右；考虑热处理后，焊接头的高周疲劳性能和断裂韧度无法在相同热处理温度达到最优。因此，通过合理设计线性摩擦焊缝高度和角度，在综合考虑稳态应力和振动应力的情况下，可以使得焊缝处于较安全区域，从而有利于提高线性摩擦焊接整体叶盘的振动安全性。

1 模态应变比及叶片危险点

现代民用航空发动机叶片设计时，可通过CFD计算、传热分析获得叶片表面气动力分布和叶片温度场，再通过有限元分析软件设置合理的边界和离心载荷，可较为精确的获得叶片稳态应力分布。但由于叶片所受气流激振力、阻尼难以准确模拟，因此，叶片在运转时的振动应力往往难以预估。由于叶片结构阻尼和气动阻尼对叶片振动时的频率和模态应力分布较小，通过比较叶片上不同位置的模态应变比(即叶片上任意一点许用振动应变与该点的模态应变的比值)，可以获得叶片上最薄弱的位置，模态应变比越高，表明叶片发生该阶共振时振动应力占许用振动应力的比值越小，振动安全性越高。因此，定义模态应变比Rmod如下：

(1)

式中：εmod为模态应变；εa为许用振动应变，由Goodman图获得，典型Goodman图定义如图1所示。

图1中，εmA和εmB分别为叶片上任意两点A，B的稳态应变，可以通过有限元分析获得。

根据模态应变比的定义，对于叶片任意的两点A和B，其模态应变比的比值为：

(2)

式中：εaA为A点的许用振动应变，根据εmA从Goodman图中获得；εaB为B点的许用振动应变，根据εmB从Goodman图中获得；εmod_A为A点的模态应变；εmod_B为B点的模态应变。

式(2)进一步调整得到：

(3)

由式(3)可知，任意两点之间的模态应变比的比值等于任意两点许用振动应变之比和模态应变之比的相除。对于叶片来说，由于阻尼对模态应力分布的影响较小，当叶片发生某阶次振动时，叶片上任意两点之间的振动应变比值与模态应变比值一致。因此，模态应变比与叶片振动应力储备系数成正比，从而模态应变比越高的点其振动应力储备越大，从而高周疲劳失效的风险越小。在确定线性摩擦焊缝位置时，应尽量避开振动应力储备(即模态应变比)较小的位置。

2 某型发动机线性摩擦焊接叶片单元件焊缝设计

2.1 叶片单元件参数

以某型发动机线性摩擦焊接叶片单元件为例(为增加考核叶片数，由线性摩擦焊接整体叶盘更改为叶片单元件)，叶片几何模型和有限元模型如图2所示，其材料为TC17钛合金，室温下的力学性能见表1，焊接前后，材料力学性能保持一致。稳态应力分析时，对叶片施加1 170 rad/s的离心载荷，在单元件底面施加全位移约束，叶片稳态应力分布如图3所示。模态分析时考虑稳态预应力，其第1阶模态应力分布如图4所示。

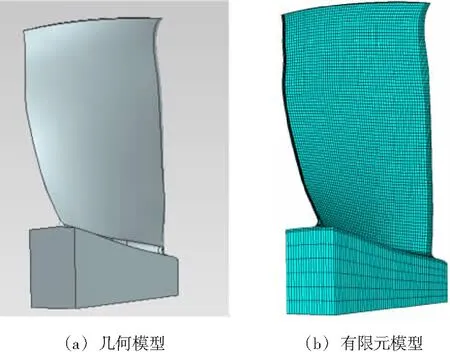
图2 叶片单元件几何模型和有限元模型

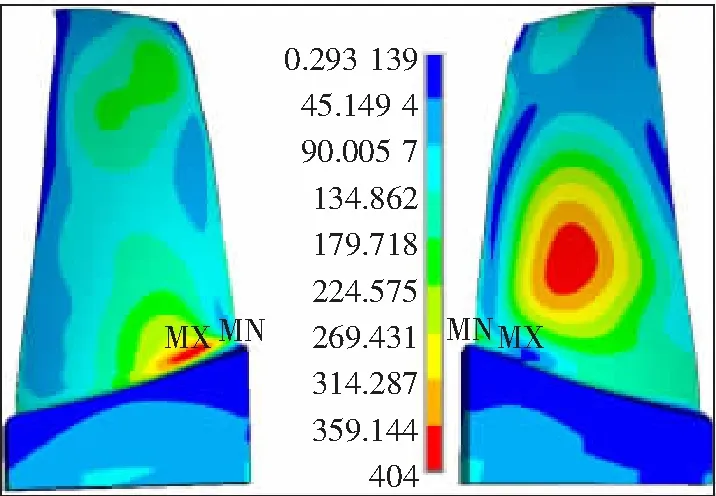
图3 叶片单元件稳态应力(等效应力)分布

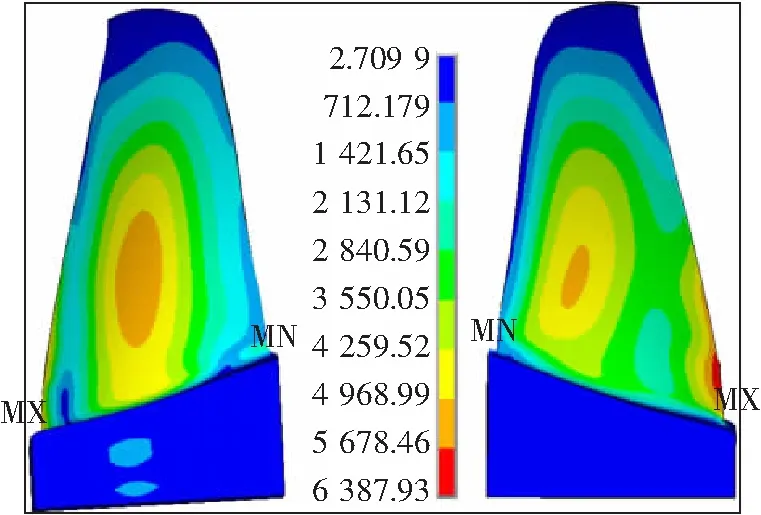
图4 第1阶弯曲模态应力(等效应力)分布

以叶片夹持端部平面为参考平面，定义焊缝高度和焊接夹角如图5所示。其中，焊缝高度为叶片进气边焊点距叶片进气边与叶片缘板交点的径向高度，焊接夹角为焊缝与夹持端部平面的夹角，当进气边焊缝高度低于排气边焊缝高度时，焊接夹角为正。

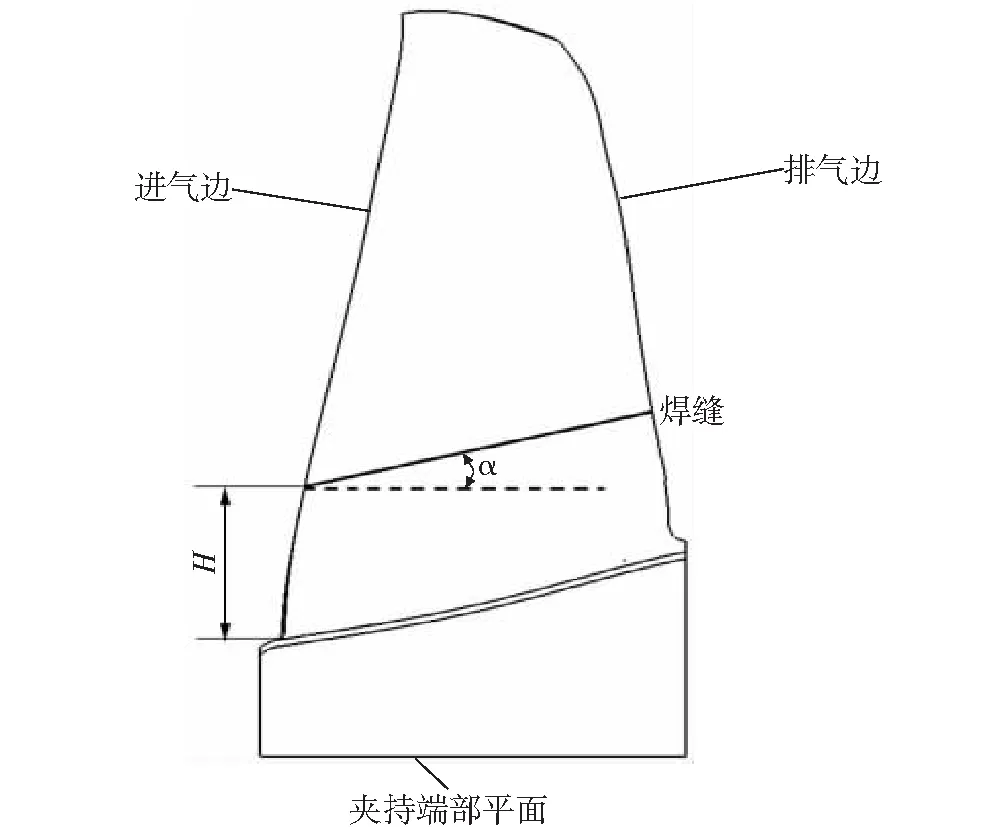
图5 焊缝高度和焊接夹角定义

根据模态应变比的定义，以典型焊缝位置为例(焊接夹角18°，焊缝高度占总叶身高度的比例分别为5%和11%)，叶片压力面焊缝在模态应变比分布如图5所示(焊缝与进气边交点为左端，相对弦长位置为0%；焊缝与排气边交点为右端，对应弦长比例100%)。

由图6可知，典型焊缝截面处，不同弦长位置的模态应变比是存在差异的，对于5%叶高截面来说，由于进气边存在明显的模态大应力区，因此，左端模态应变比较低，而右端因远离模态大应力区并且静应力较小，因此模态应变比较高。11%叶高截面与5%截面类似，但右端模态应变比更高。

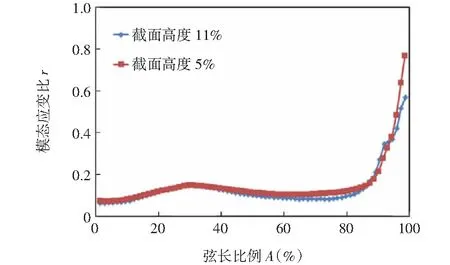
图6 典型焊缝截面(叶片压力面)模态应变比分布

2.2 焊缝高度和焊接夹角影响分析

通过对不同焊缝高度处的叶身截面进行分析，不断调整焊接夹角，并提取对应焊接截面的最小模态应变比，可以得到不同焊缝高度对应的最小模态应变比如图7所示。

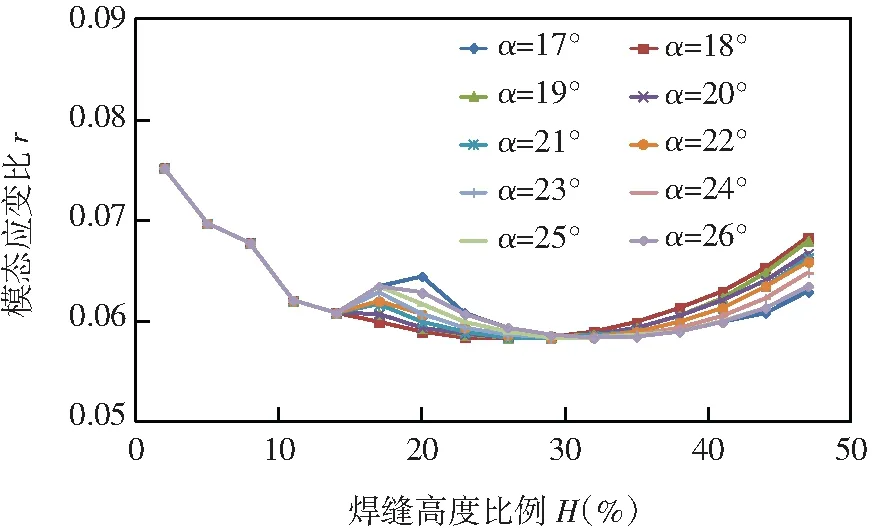
图7 不同焊缝高度下的模态应变比分布

由图7可知，在2%～50%叶片高度范围内，不同焊缝高度下的模态应变比差异最大可达29.3%(最大值0.075 2，最小为0.058 5)。同一焊接夹角下，随着焊缝高度的增加，焊缝位置的最小模态应变比呈现“C”形分布，25%～35%焊缝高度处的模态应变比最低，而在此区域外，模态应变比则逐渐增大。值得一提的是，在15%～25%焊缝高度，存在一处模态应变比局部峰值区域。

类似的可以得到不同焊接夹角下的最小模态应变比，如图8所示。

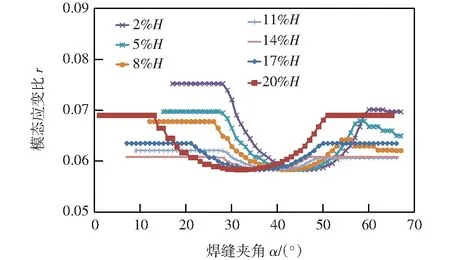
图8 不同焊接夹角下的模态应变比分布

由图8可知，不同焊接夹角对模态应变比的影响可达到29.6%(最大值0.075 2，最小为0.058)。同一焊缝高度下，焊缝对应的最小模态应变比亦呈现“C”形分布，与图6的差异在于，同一焊缝高度下，曲线两端存在模态应变比基本不变的“平台区域”，而中间焊接夹角对应的模态应变比最低。以5%焊缝高度为例，焊接夹角处于20°～30°最佳，55°～65°其次，而在30°～55°之间，模态应变比类似于抛物线分布。综合焊缝位置和焊接角度分析，对于该叶片的1阶弯曲振动，宜选择10%及以下焊缝高度，焊接夹角不易超过30°。

2.3 模态阶次的影响分析

针对1阶扭转模态开展分析，依次得到不同焊缝高度和不同焊接夹角下的模态应变比分别如图9和图10所示。

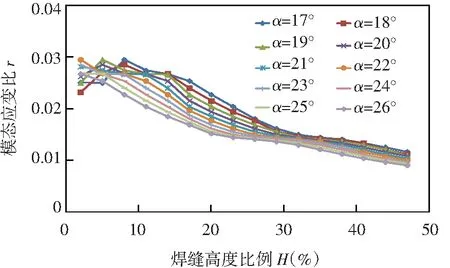
图9 不同焊缝高度下的模态应变比分布

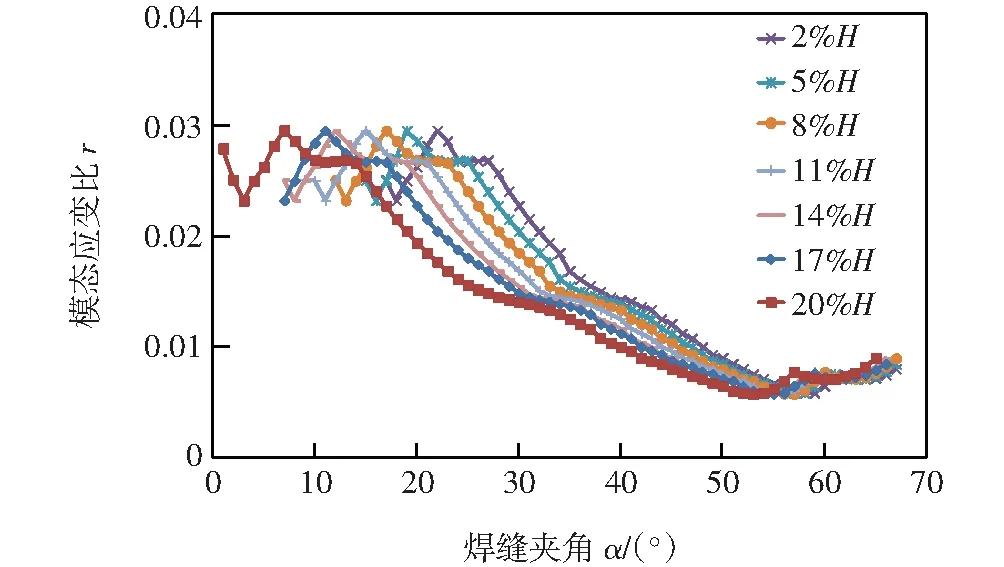
图10 不同焊接夹角下的模态应变比分布

由图9和图10可知，不同焊接高度和焊接夹角对模态应变比的影响更大，分别可达227%和392%；对于1阶扭转模态，焊缝高度越高，模态应变比越低；焊接夹角在25°以下区域存在着模态应变比较高的平台区域。以5%焊缝高度为例，焊接角度在21°～25°范围内较为合适，而当焊接夹角小于21°时，角度差异最大可使得模态应变比出现20%左右的波动。

3 结论

(1)线性摩擦焊缝位置对于整体叶盘整体安全性影响较大，文中提出了一种通过计算模态应变比来判断叶片危险点方法，可以用于判断叶片振动安全性。

(2)基于文中提出的方法，对某线性摩擦焊接叶片单元件焊缝的焊缝高度和焊接夹角进行了敏感性分析。分析了第1阶弯曲模态和第1阶扭转模态振型下，模态应变比随焊缝高度和焊接夹角的变化规律，给出了较合适的焊缝高度和焊接夹角。通过分析不同焊缝高度及不同焊接夹角下的模态应变比变化规律，可根据需重点关注的模态选择合适的焊缝位置，使得焊缝区域的模态应变比较高，提高叶片振动安全性。