高铁提速条件下路基不均匀沉降诱发的地基振动特性

蒋红光 李宜欣 迟浩然 刘 舜 梁 明 姚占勇

(山东大学齐鲁交通学院， 济南 250002)

列车的高速运行会对沿线敏感建筑物与居民住宅等设施产生振动危害[1].随着路基不均匀沉降的发展和列车的进一步提速，车-轨之间的动力响应加剧，导致周边场地振动特性随之发生变化.因此，有必要对高铁提速条件下典型路基不均匀沉降诱发的场地振动特性开展研究，以评价线路不平顺下的列车提速可行性.

国内外学者针对移动振源和场地振动传播规律开展了系统的研究.雷晓燕[2]采用波数-频率域解析法，研究了移动荷载下轨道结构和地基的振动响应.高广运等[3]利用2.5D有限元法研究了高铁荷载引起的地面振动特性.边学成等[4]指出，当列车速度与瑞利波波速接近时，会大幅增加轨道的垂向振动.Bian等[5]通过全比尺的物理模型试验发现列车速度的提高和路基状态的退化均会增大系统的振动响应.随着线路服役周期的增加，轨道平顺状态逐渐恶化.Feng等[6]利用时域有限元法研究了不同车速和频率下的地基振动规律，提出了地面敏感频率范围.Zhai等[7]认为轨道不平顺引起的轮轨作用会显著影响地面加速度，但对地面位移影响较小.边学成等[8]认为高速铁路引起的振动必须重视水平方向.蔡袁强等[9]发现轨面不平顺时，轮轨作用力和轨枕间距对地基振动影响明显.巴振宁等[10]指出，高频率下地基振动对车速不敏感，但振动消散困难.房建等[11-12]发现轨道不平顺条件下无砟轨道振动主要集中于钢轨，路基段振动受不平顺影响明显大于桥梁段.由此可见，列车速度提高和线路平顺状态恶化均会导致动力响应加剧.然而，现有研究大多针对钢轨短波不平顺且列车速度不超过360 km/h时的情况，由路基不均匀沉降诱发的中波不平顺及超高速条件下的场地振动特性研究相对较少.

本文建立了考虑路基不均匀沉降的列车-轨道-路基三维有限元模型，研究了典型路基沉降波长和幅值条件下的地基振动特性，分析了路基不均匀沉降和列车车速对场地振动时域、频域特性的影响以及振动传播衰减规律，并结合现行的振动控制标准对提速可行性进行讨论.

1 考虑不均匀沉降的列车-轨道-路基三维有限元模型

1.1 模型建立

根据中国高速铁路CRTS Ⅱ型无砟轨道的尺寸建立考虑不均匀沉降的列车-轨道-路基三维有限元模型(见图1)，包括UIC60钢轨、2.6 m宽轨道板、2.6 m宽水泥沥青砂浆层(CAM层)、3.25 m宽混凝土底座以及路基和地基.扣件采用刚度为30 kN/mm的垂直弹簧阻尼单元模拟.车轮与钢轨的相互作用采用表面与表面接触类型，法向接触采用硬接触属性且允许接触后分离，切向接触采用无摩擦接触属性.考虑到不均匀沉降的存在，当垂直接触压力降为零时，路基、混凝土底座、CAM层和轨道板之间的界面允许分离，切向接触采用库仑摩擦模型接触属性[13]，参数见表1.地基周围采用3层阻尼边界模拟无限边界[14]，由内而外依次是第1、2、3层地基边界，每层厚度为5 m，第k层的阻尼系数为

αk=α0ζk

(1)

βk=β0ζk

(2)

式中，αk、βk分别为第k层地基边界的质量阻尼系数和刚度阻尼系数；α0、β0分别为地基的质量阻尼系数和刚度阻尼系数；ζ为递增因子.取ζ=2，则各层阻尼系数向外依次倍增(见表2).

(a) CRTS Ⅱ无砟轨道截面图

(b) 3D有限元模型

车辆模型选取高速列车CR400型，设计时速为400 km/h，运行速度为350 km/h，轴重170 kN，结构尺寸见图2.车体、转向架和轮对均采用刚体来模拟，一系悬挂和二系悬挂采用弹簧阻尼元件来模拟.一系悬挂连接轮对和转向架，刚度Kp=1 040 kN/m，阻尼Cp=50 kN·s/m；二系悬挂连接列车转向架和车身，刚度Ks= 400 kN/m，阻尼Cs= 60 kN·s/m.

1.2 不均匀沉降

路基不均匀沉降采用余弦函数来模拟，即

表1 轨道模型所用参数

表2 阻尼边界参数

图2 CR400结构图(单位：m)

(3)

式中，s(x)为路基沉降值；A0为沉降幅值；L0为沉降波长；x0为沉降发生的初始位置.本文选取我国高铁设计规范规定的路基不均匀沉降控制值，即波长为20 m，幅值为15 mm.

施加不均匀沉降之前，首先进行地应力分析步，使路基、地基处于初始应力状态.然后，设置路基不均匀沉降分析步，利用Fortran语言编写路基不均匀沉降子程序，即定义路基上表面的沉降区域以及各纵向坐标节点向下产生的位移量，从而形成不均匀沉降边界.在随后的分析步中，施加列车自重和移动时间步，实现不同列车速度的模拟.

1.3 可靠性验证

Bian等[5]在京津城际客运专线试运行期间对混凝土底座的振动进行了现场测试.由图3可知，列车速度为316 km/h时，混凝土底座的速度时程曲线与现场测试结果接近.振动速度频谱曲线中，现场实测的主要峰值频率为3.5、7.0和10.5 Hz，与数值分析获得的主要频率3.5、6.5和10.1 Hz接近，说明该数值模型的计算结果可靠.

(a) 振动速度时程曲线

(b) 振动速度频谱曲线

2 场地振动影响因素分析

2.1 路基不均匀沉降的影响分析

地基振动的响应参考点位置示意图见图4.由路基向外侧依次为地基坡脚点、地基1#点～5#点，分别距轨道中心线7.8、14.1 、20.4、26.8、31.8、36.8 m.

（3）领先的智能音频分析。自带音频自动对齐功能，根据不同音视频素材的波形，智能分析出偏移量进行补偿，保证音频波形准确对齐，减少工作强度。

图4 地基振动的响应参考点位置示意图

以列车速度360 km/h为例，依次提取路基发生不均匀沉降前后各参考点的垂向振动速度vy、加速度ay以及动位移Uy的时程曲线，结果见图5.由图可知，随着距轨道中心距离的增加，加速度、速度和位移响应的振动幅值均明显下降，反映了振动沿地基横向传播时的衰减效应.未施加沉降时，振动速度衰减较快，振动幅值在0.5 s内迅速衰减并稳定；施加不均匀沉降后，所有响应点的幅值在列车行驶过程中没有发生明显衰减，振动幅值约为未沉降时的2倍.

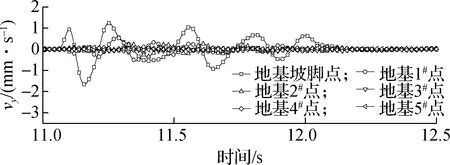
(a) 沉降前速度时程曲线

(b) 沉降后速度时程曲线

(c) 沉降前加速度时程曲线

(d) 沉降后加速度时程曲线

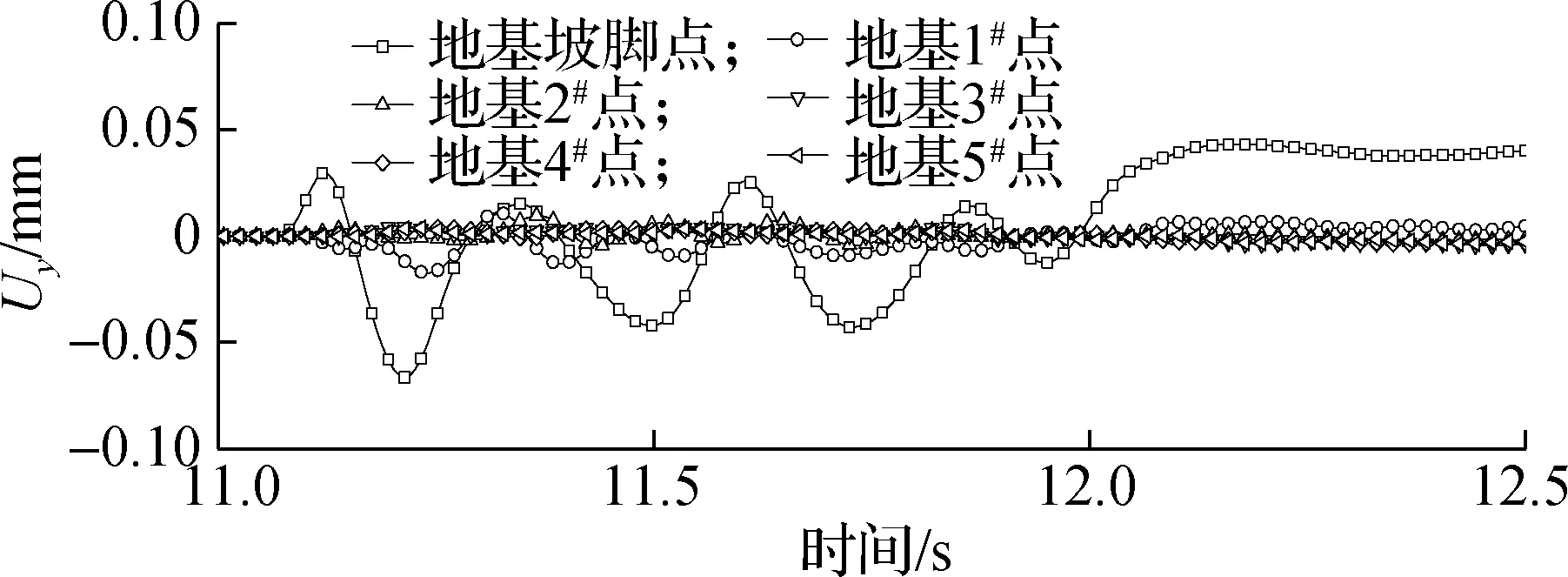
(e) 沉降前位移时程曲线

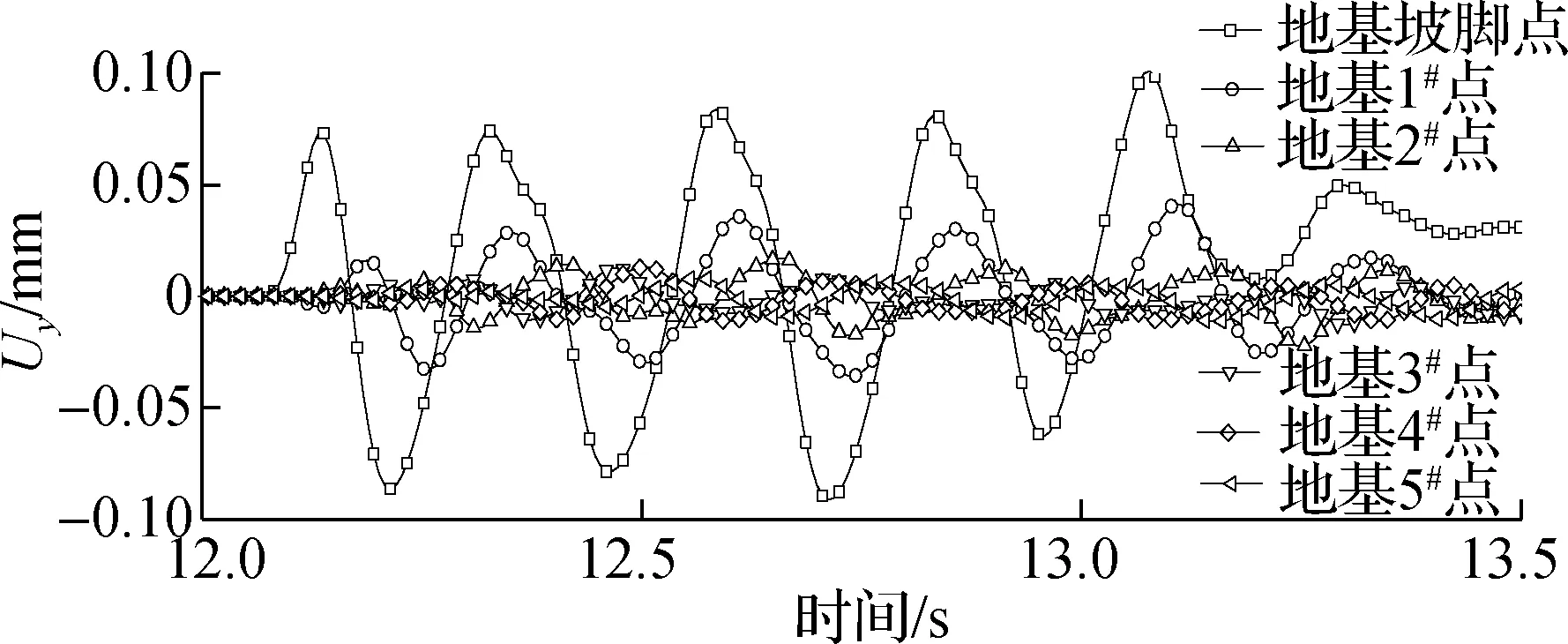
(f) 沉降后位移时程曲线

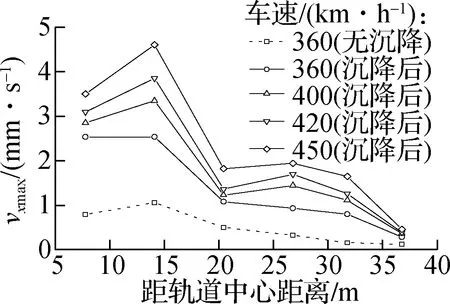
图6为振动速度、加速度和动位移的最大响应幅值沿横向距离的变化曲线.响应幅值定义为时程曲线的峰值之差.由图可知，对于水平横向振动，振动速度、加速度和位移的最大响应幅值vxmax、axmax、Uxmax分别由沉降前的0.15～1.06 mm/s、8.29～55.69 mm/s2和0.01～0.03 mm增大到沉降后的0.80～2.53 mm/s、28.4～156.40 mm/s2和0.02～0.07 mm，分别增加了2.4、2.8和2.3倍.对于垂向振动，振动速度、加速度和位移的最大响应幅值vymax、aymax、Uymax分别由沉降前的0.19～2.90 mm/s、8.97～124.59 mm/s2和0.01～0.11 mm增大到沉降后的0.83～5.79 mm/s、29.60～251.60 mm/s2和0.02～0.19 mm，分别增加了2.0、2.1和1.7倍.对于水平纵向振动，振动速度、加速度和位移的最大响应幅值vzmax、azmax、Uzmax分别由沉降前的 0.14～1.21 mm/s、9.83～78.46 mm/s2和0.005～0.018 mm增大到沉降后的0.42～1.96 mm/s、 28.50～148.30 mm/s2和0.009～0.035 mm，分别增加了1.6、1.9和1.9倍.由此可见，路基不均匀沉降将诱发更大的地基振动，且水平横向所受的影响普遍大于垂向和水平纵向，其中水平横向振动加速度受激励作用最明显.就衰减速率而言，尽管垂向振动强度高于2个水平方向的振动强度，但是三者振动的衰减均主要集中在距离轨道中心20 m范围内.

图7为沉降前后各参考点垂向振动速度、加速度和动位移的频谱图.图中，f1～f5为沉降后频谱图中的5个峰值频率.由图可知，地基的动力响应主要以低频段为主，沉降后的振动峰值频率与强度更为显著.对于垂向振动速度、加速度和位移，沉降前的主要峰值频率为3.98 Hz，对应的振动强度Evy、Eay、EUy分别为0.49 mm/(s·Hz)、12.28 mm/(s2·Hz)和0.02 mm/Hz；路基不均匀沉降发生后，峰值频率3.98 Hz对应的振动强度增量分别为1.38 mm/(s·Hz)、34.58 mm/(s2·Hz)和0.05 mm/Hz.同时，沉降后显著出现了4个峰值频率，即6.64、7.98、11.95、15.96 Hz.

图8为车辆结构尺寸示意图.图中，L0～L4为扰动波长.地基响应的峰值频率可能受列车速度、轮轴间距、车辆与转向架的尺寸等激振因素影响.扰动波长Li对应的扰动频率fLi可表示为

(4)

式中，v为列车车速.扰动波长L0～L4及其对应的扰动频率fL0～fL4见表3.

路基表面不均匀沉降波长λ所对应的频率计算公式为

(5)

由式(5)可知，当v=100 m/s，λ=20 m时，频

(a) 水平横向速度

(d) 水平横向加速度

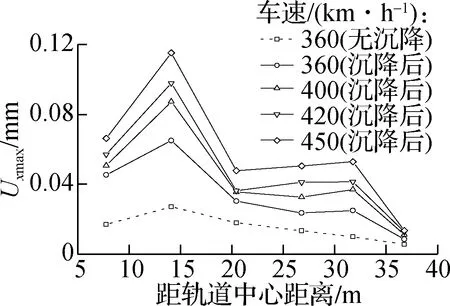
(g) 水平横向动位移

(a) 沉降前振动速度强度

(c) 沉降前振动加速度强度

(e) 沉降前动位移强度

图8 车辆结构尺寸示意图

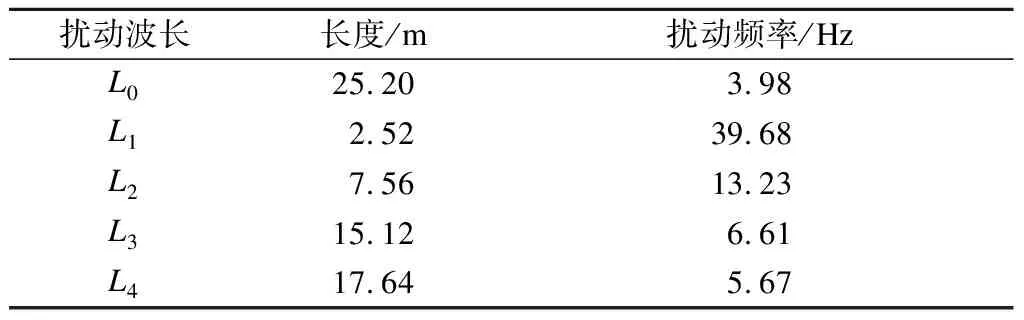
表3 扰动波长和扰动频率

率为5 Hz.将频谱图中的峰值频率f1～f5与fλ、fL0～fL4比较发现，基频f1与单节车厢长度L0相对应，且f3、f4和f5为基频f1的倍频.而f2的特征波长约为15 m，与同一节车厢的转向架间距L3接近.因此，无砟轨道的地基振动主要受单节车厢长度L0控制且每节车辆转向架前后车轮间距也会影响地基振动的峰值频率.此外，未发现沉降波长对应的峰值频率，即地基振动的特征频率无法反映路基表面不均匀沉降的波长特征.发生不均匀沉降后，基频f1及其倍频f4的振动强度增加明显，尤其是垂向振动速度和加速度.

2.2 列车提速的影响分析

考虑到中国列车的提速规划，分别计算了沉降条件下车速为360、400、420、450 km/h时的场地振动，结果见图6.由图可知，当车速从360 km/h增加到450 km/h时，各位置处的横向水平振动速度、加速度和位移幅值分别增加了0.74～2.08 mm/s、29.6～96.6 mm/s2和0.02～0.05 mm；垂向分别增加了1.05～4.21 mm/s、30.8～154.1 mm/s2和0.02～0.07 mm；纵向水平方向分别增加了0.04～1.01 mm/s、5.9～59.6 mm/s2和0.002～0.027 mm.列车提速主要影响了垂直方向的振动响应，其振动速度、加速度和位移的最大增幅分别为1.7、1.6和1.4倍.相较于列车提速，路基不均匀沉降诱发的振动增量更加显著.

3 基于现行振动控制标准的评价分析

高速铁路的环境振动评价中一般采用垂向振动加速度和垂向Z振级作为评价指标，计算公式为

LZ=20lg(a′rms/a0)

(6)

式中，LZ为垂向Z振级；a0为基准加速度，此处取a0=10-6m/s2；a′rms为修正的加速度有效值.

中国《城市区域环境振动标准》规定了环境振动限值.其中，铁路干线两侧距离铁道外轨30 m处的垂向Z振级不得超过80 dB.日本新干线则要求距轨道中心12.5 m的垂向Z振级不得超过90 dB.图9给出了沉降前后及不同车速下垂向Z振级距离轨道中心的变化曲线.由图可知，路基未发生不均匀沉降时，垂向Z振级在距离外轨中心线30 m处约为74.5 dB，并未超过中国规范所限制的80 dB；在距离外轨中心线12.5 m处也未超过日本新干线的规定.而发生不均匀沉降后，相同位置处的垂向Z振级普遍增大了5～12 dB，平均增大了8.82 dB，较未发生沉降时升高约11%；距离外轨中心线30 m处的振级达到85 dB，超过了规范标准.列车速度的提高会导致加速度振级的进一步增加，速度从360 km/h提升到450 km/h后，6个不同位置处响应点的垂向Z振级增加了5%～10%.由此可见，路基不均匀沉降对地基垂向振动激励更明显，高铁列车提速会使之进一步加剧.高铁列车提速易使地基振动超出环境振动控制标准的要求，对路基平顺性能提出更高的要求.

图9 垂向Z振级随距外轨中心线距离变化图

4 结论

1)路基不均匀沉降会加剧地基振动，对水平横向振动激励最明显.路基不均匀沉降引起的地基振动衰减主要集中在距离外轨中心20 m范围内.

2)路基平顺状态下，地基的频谱响应以低频为主.不均匀沉降发生后，出现较高的峰值频率，特征频率与单节车厢长度相对应.路基不均匀沉降引起的场地振动峰值频率无法反映其沉降波长特征.

3)在路基不均匀沉降条件下，列车提速会加剧地基振动响应，其中垂向振动速度最为敏感.但其振动增量要小于路基不均匀沉降诱发的振动.

4)对于现行规范中幅值15 mm、波长20 m的限值，当高铁列车车速为360 km/h时，周围场地的垂向Z振级已超过我国和日本的环境振动控制要求.随着列车车速提高，垂向Z振级进一步增大.现行的路基不均匀沉降控制标准未能满足列车提速下环境振动控制要求.高铁线路提速前，应充分评估路基平顺状态的振动影响.