变间隙法布里-珀罗干涉仪光程差线性分析

韩 军，高 波，张 芳，高教波

（1.西安工业大学 兵器科学与技术学院，陕西 西安 710021；2.西安应用光学研究所，陕西 西安 710065）

引言

变间隙法布里-珀罗（F-P）干涉仪[1-5]作为干涉式光谱成像系统的新型分光器件，真正有效地实现了系统体积的小型化和系统结构的紧凑化，尤其在长波红外波段，已成为研究热点。

一般地，变间隙法布里-珀罗（F-P）干涉式光谱成像系统包括前端成像物镜、变间隙F-P干涉仪、中继镜、探测器以及信号处理系统，如图1所示。前端成像物镜将目标成像在系统的一次像面上；变间隙F-P干涉仪由一个楔形平板和平行平板构成，具体结构如图2所示（α为干涉仪楔角），实现干涉分光作用；中继镜会聚光束实现二次成像和产生干涉条纹的作用；探测器实现目标空间信息和干涉信息的同时获取和记录功能；信号处理系统实现探测器获取的图像信号的处理和显示功能。

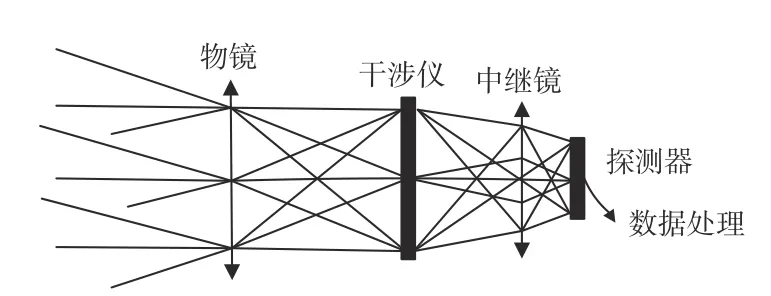
图1 变间隙F-P干涉式光谱成像系统Fig.1 Variable-gap F-P interferometric spectral imaging system

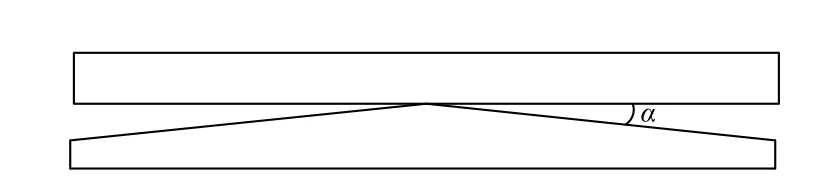
图2 变间隙F-P干涉仪结构图Fig.2 Structure diagram of variable-gap F-P interferometer

变间隙干涉式光谱成像系统采用快速傅里叶变换方法对其获取的干涉信息进行解调，最终获取目标的光谱信息。但该方法要求探测器上不同像元对应的光程差等间隔变化。经分析，探测器上不同像元对应的光程差是系统的艾里斑中心距的函数，而在一定楔角大小条件下，艾里斑中心距随探测器位置的变化是非线性的。本文的主要目的是分析当艾里斑中心距随探测器位置非线性变化时，由此产生的不同像元对应的光程差是否对系统的光谱数据解调结果有影响。

1 光程差与两艾里斑中心距

变间隙法布里-珀罗（F-P）干涉腔反射面的反射率，相较于经典F-P干涉仪[6-11]较低，可以不考虑干涉腔内高级次光束对干涉强度的影响，只考虑前两级透射光束的干涉问题。因此，物点光束通过变间隙F-P干涉仪在其出射面上会形成两个艾里斑。由于干涉仪厚度较小，且两干涉腔相对干涉仪中心棱对称，图3仅显示了干涉腔一侧的内部光路。图3中，点S1、点S2分别为第一、二级透射光束产生的艾里斑中心点；α为干涉仪楔角；β为第一级透射光在干涉腔下表面上产生的入射角；点S1与点S2之间的距离为两干涉光束产生的两艾里斑中心距d；点S1距中心点O（中心棱上的点）之间距离为入射光束在干涉腔出射面上对应的入射点至中心棱之间的距离x；y1和y2分别对应两条光线的光程。

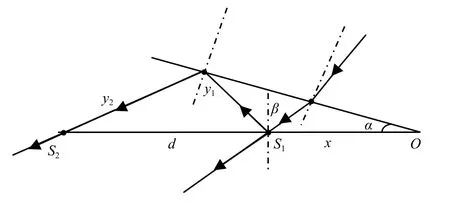
图3 两干涉光束之间光程差计算示意图Fig.3 Schematic diagram of optical path difference calculation between two interference light beams

根据几何关系，图3中两干涉光束对应的光程差为

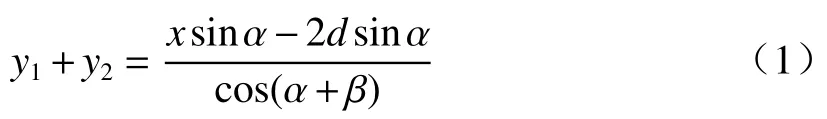
由（1）式可以看出，不同位置处的探测器像元（取决于x值）接收到的两干涉光束的光程差与系统两艾里斑中心距d有关。

2 变间隙F-P干涉仪楔角与两艾里斑中心距

不同视场光线经过干涉仪的具体光路如图4所示。以楔形平板的中心棱为对称中心，图中仅显示了中心棱单侧的光路，另一侧与其对称分布。入射光的视场角为θ，经过楔形板平面第一次折射后的折射角为θ1，到达楔形板楔形出射面的入射角为θ2，经过折射，在干涉腔内的折射角为θ3，到达平行平板的入射角为β。第一束出射光线产生的艾里斑中心点为S1，在干涉腔内经过两次反射后出射的第二束光线产生的艾里斑中心点为S2，由于平行平板较薄，图4中将两艾里斑中心点简画在平行平板在干涉腔内的反射面上。

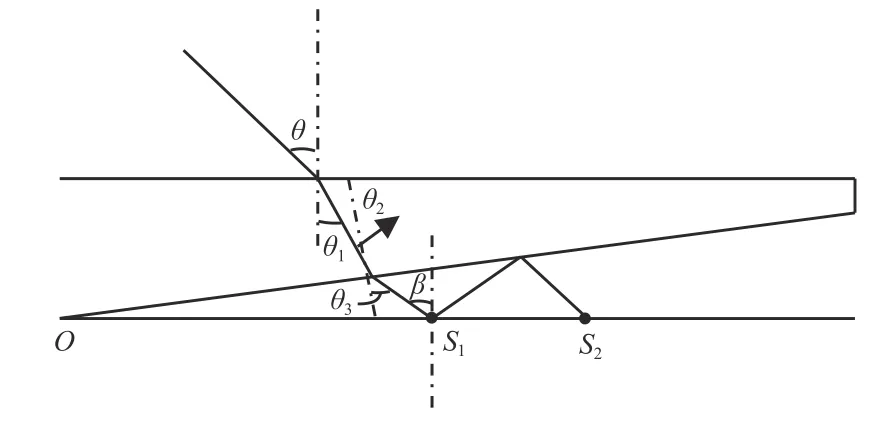
图4 艾里斑形成光路图Fig.4 Optical path diagram of formation for two Airy disks

光线到达楔形平板后要经过2次折射才能进入干涉腔，根据折射定率，不同视场角对应的折射角不同，且楔角大小不同，对应光线的折射方向也会发生改变，最终在平行平板出射面上形成的两个艾里斑中心距S1、S2也会随之改变。

假定长波红外变间隙F-P干涉式光谱成像系统的中继镜垂轴放大率为1:1，干涉仪材料为锗，根据折射定率，可以得到不同楔角下，探测器不同像元位置处艾里斑中心距大小，如图5所示，以变间隙F-P干涉仪中心对称棱在探测器上对应的位置为零位。图5中，每条曲线对应不同的楔角，自下而上楔角大小从10 mrad至50 mrad，每隔5 mrad为一个值。从图上可以看出，当楔角大于等于25 mrad时，艾里斑中心距与探测器像元距零点位置的距离呈线性关系；当楔角小于25 mrad时，艾里斑中心距与探测器像元距零点位置的距离呈非线性关系（这是由楔角与视场角相对大小变化引起的）。此外，随着楔角的增大，探测器阵列相同位置对应的艾里斑中心距不断增大，若中心距大于截止尺寸（当中继镜的垂轴放大率为1:1时，探测器像元大小为艾里斑中心距的截止尺寸，艾里斑中心距的具体截止尺寸与中继镜垂轴放大率的实际值有关），则该像元位置无法产生干涉条纹，且成像质量不佳。因此，需要考虑艾里斑中心距随探测器位置非线性变化时，不同像元对应的光程差是否线性变化。

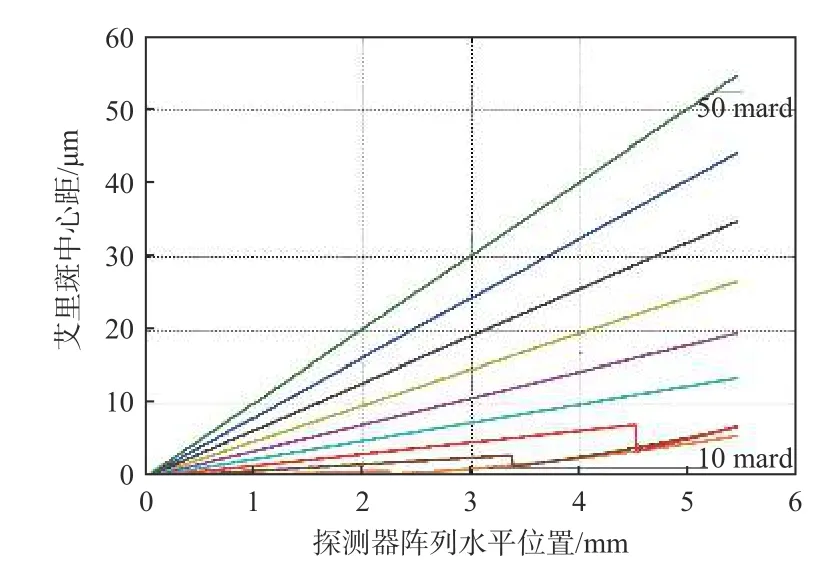
图5 艾里斑中心距与像元位置关系曲线Fig.5 Curves of relationship between centre distance of Airy disk and pixel position

依据（1）式可以得到光程差与探测器阵列像元距零点位置的距离之间的线性关系，如图6所示。

图6表明，对于不同楔角大小，无论艾里斑中心距与探测器像元距零点位置的距离是否呈线性关系，光程差与探测器像元距零点位置的距离始终呈线性关系，并不会影响变间隙F-P干涉式光谱成像系统光谱数据的解调准确性。

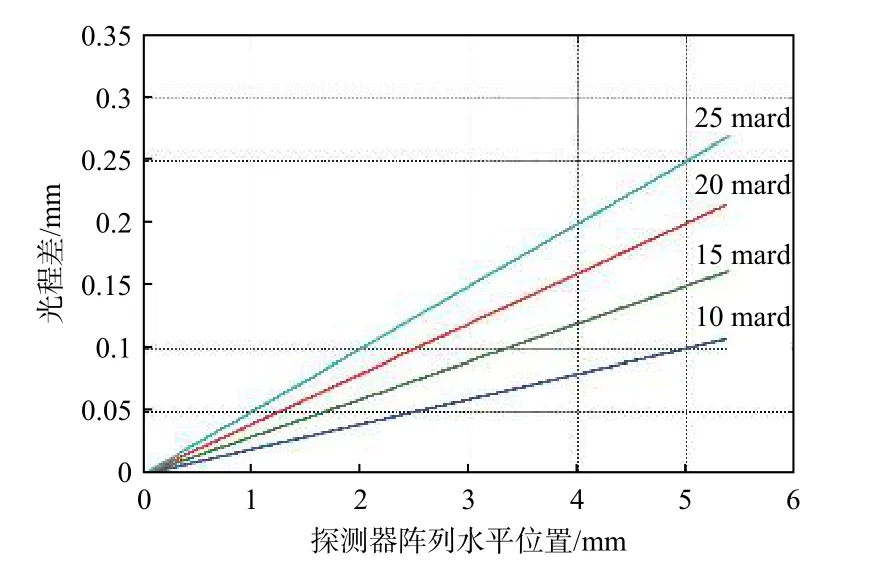
图6 光程差随探测器像元位置的变化曲线Fig.6 Changing curves of optical path difference with detector pixel position

3 实验验证

综上所述，选取楔角α大小时，只需根据图5，使得所选楔角大小对应的艾里斑中心距小于探测器所能分辨的最小空间单元尺寸即可，无需考虑所选楔角大小对应的艾里斑中心距与探测器阵列像元距零点位置的距离是否呈线性关系。

根据实验室现有条件，搭建了变间隙F-P干涉式光谱成像系统实验样机[12]。整个样机系统的波长响应范围为8 μm～12 μm。干涉仪的楔板和平行平板的材料均为锗，在8 μm～12 μm波段范围内反射率为40%，楔角为15 mrad，楔板的光入射面和平行平板的光出射面镀制了99.5%的增透膜。

首先，系统拍摄50 ℃面黑体的干涉图。然后，将在长波红外波段具有明显特征峰的聚丙烯薄膜放在50 ℃面黑体与样机成像物镜之间，得到含有薄膜光谱特征的干涉图。分别从上述两干涉图提取干涉条纹，进行切趾、相位校正等处理，最终进行傅里叶变换[13-15]，并对最终的光谱数据进行数学处理，得到聚丙烯薄膜的光谱透过率曲线，如图7中红色曲线所示。

采用光谱分辨率为1 cm−1的高精度光谱辐射计，Turbo FT，测量聚丙烯薄膜的光谱透过率曲线，对比曲线如图7蓝色曲线所示。

通过比较两光谱曲线，可以确定样机的采样步长为1.95 μm，由此计算得到光谱分辨率为15 cm−1，与理论计算值12 cm−1相近。从图7可以看出，变间隙F-P干涉式光谱成像系统得到的光谱曲线不仅形状与高精度光谱辐射计得到的光谱曲线相同，而且二者在1 000 cm−1、1 175 cm−1和1 220 cm−1等附近的特征峰位置完全相符。

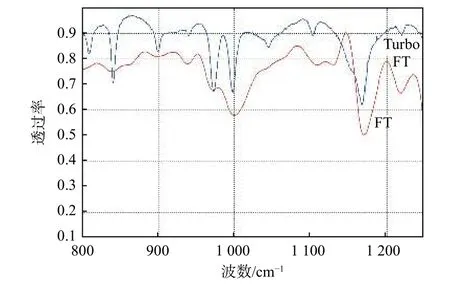
图7 聚丙烯薄膜透过率曲线Fig.7 Curves of polypropylene film transmittance

4 结论

通过测量在长波红外波段有特定吸收峰的聚丙烯薄膜样品的光谱透过率曲线，并将测量结果与高精度光谱辐射计测量结果进行比较，验证了实验样机复原光谱的准确性。同时，验证了变间隙F-P干涉式光谱成像系统方案原理的可行性。实验结果中，系统实际光谱分辨率与理论设计值的偏差，与系统中各成像光学部件的成像质量、干涉仪的面形精度，以及系统的装配精度等相关因素均有关系。

图5表明，楔角为15 mrad时，艾里斑中心距与探测器阵列像元距零点位置的距离呈非线性关系，但从上述实验结果可以看出，此时光程差与探测器阵列像元距零点位置的距离仍保持线性关系，并不影响变间隙法布里-珀罗干涉式长波红外光谱成像系统的光谱数据解调精度。这是由于干涉仪楔角值较小，削弱了艾里斑中心距对不同像元处干涉光束之间的光程差的影响。