基于透镜畸变效应的仿人眼扫描系统设计

杨 骜，曹 杰，郝 群，陈传训，高贯磊

（北京理工大学 光电学院 机器人与系统教育部重点实验室，北京 100081）

引言

激光雷达通过发射信号扫描待测目标所在区域，并接收返回信号来实现对目标的探测、识别和成像[1-3]。激光雷达对目标的扫描方法多采用行列式扫描、弓形扫描、仿人眼扫描等方法[4-5]。其中，仿人眼扫描相比于其他扫描方法具有旋转与尺度不变性、背景信息压缩及变分辨率信息获取的优点[6-7]，近年来被用在激光雷达、目标识别与自动聚焦等领域[8-11]。

目前，仿人眼采样的方式有利用MEMS镜、复眼镜头、旋转双棱镜等方式[12-14]。利用MEMS镜实现仿人眼扫描的方式无法同时实现大光斑与多线扫描，利用复眼镜头的扫描方式存在结构复杂、成本高、无法改变扫描密度和步进角度的缺点，利用旋转双棱镜的扫描方式无法实现多线扫描，且双棱镜的安装误差会影响扫描精度与准确度。基于以上原因，本文提出一种利用透镜自身畸变实现不同视场入射光斑放大，同时利用阿贝棱镜旋转实现仿人眼扫描的方法。

本文首先对仿人眼扫描原理及系统进行建模分析，然后对利用透镜畸变效应实现非均匀仿人眼光斑扫码进行了理论分析，建立了透镜表面面形求解方法，同时对仿人眼扫描系统进行了仿真分析。仿真结果表明，该方法可以通过旋转阿贝棱镜实现对目标区域的仿人眼扫描。

1 仿人眼扫描系统

仿人眼扫描的原理是基于人眼视网膜的非均匀特性，在中心位置感光面积小、分布密集，在外围的感光面积大、分布稀疏。这种特征能够在压缩冗余背景信息的同时，获得高分辨率的目标[6]。因此，对于同样次数的采样人眼视网膜结构获取信息的效率更高。仿人眼扫描的光斑模型如图1所示。仿人眼扫描光斑由分布于N个同心环带的光斑组成，中心环光斑直径最小，每向外增加一个环带，环带上分布的光斑直径相对于中心环带按不同比例放大，中心光斑直径小、分布密集，外环光斑直径大、分布稀疏，类似人眼视网膜非均匀分布结构。

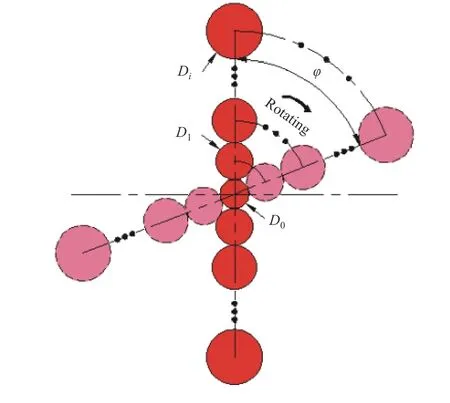
图1 仿人眼扫描的光斑模型Fig.1 Mode of spots for retina-like scanning

非均匀分布仿人眼扫描光斑的参数可以表示为

式中：D0为中心光斑的直径；Di为第i环光斑的直径；qi为第i环光斑直径相对于中心光斑直径的增大系数。

根据仿人眼扫描光斑的分布特性，利用透镜畸变效应与阿贝棱镜旋转设计了一种实现仿人眼扫描的系统，系统结构如图2所示。当激光器照射衍射光学元件（diffractive optical elements，DOE）时，一束激光经过DOE分束后可以获得1×n的线阵激光。线阵激光通过透镜时，不同视场的光斑由于透镜畸变被以不同放大倍率进行放大，由此将光斑直径相等的1×n的线阵激光光斑转变为光斑直径非均匀分布的线阵激光光斑，变形后的线阵光斑经过阿贝棱镜出射。由于阿贝棱镜旋转时具有光斑角度放大的作用，当阿贝棱镜旋转α角时，出射的线阵光斑绕中心旋转2α，通过连续旋转阿贝棱镜，即可在像面实现仿人眼扫描。

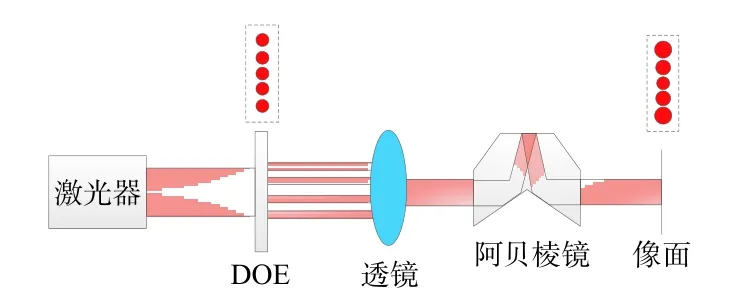
图2 仿人眼扫描系统结构Fig.2 Structure diagram of retina-like scanning system

2 透镜参数计算

2.1 透镜畸变

对于单一透镜，由于存在球差，物方平面上的轴外物点发出的主光线在理想像面上的交点高度为Y'z，近轴光线在理想像面上的交点高度为y’，两条光线在理想像面的交点位置存在偏差，这个偏差就是透镜的畸变，如图3所示。透镜的相对畸变P可以由下式表示：

将仿人眼扫描光斑的参数表达式（1）进行变形，可以得到环间增长系数的相对值表达式：

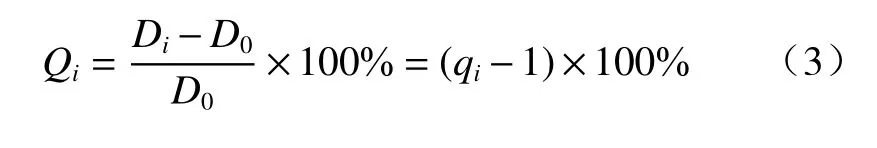
图3 透镜畸变原理图Fig.3 Schematic diagram of lens distortion

对（3）式与（2）式进行比较，如果将D0视为理想像高y′，则环间增长系数的相对值Qi可以视作透镜的相对畸变P。因此，通过设计透镜结构参数，控制透镜的相对畸变值P等于环间增长系数的相对值Qi，则物面均匀的线阵激光光斑通过透镜后，由于透镜的畸变效应，出射光斑在不同视场下被以不同比例放大，形成非均匀分布的线阵激光光斑。

2.2 透镜初始参数计算

透镜物像关系如图4所示。图4中透镜前后表面曲率半径为r1、r2，透镜厚度为d，透镜材料的折射率为n，物高为y，物距为l，像高为y′，像距为l′。

图4 透镜光路图Fig.4 Optical path of lens

透镜焦距由下式给出[15]：

透镜放大倍率可以表示为

透镜垂轴放大倍率可通过像高与物高之比求出：

当已知物像关系l′、y′、y，同时给定透镜参数n、d、r1=−r2，通过求解（4）式～（6）式，可以得到满足物像关系的透镜初始结构参数。

2.3 透镜非球面优化

对于球面透镜，在确定了透镜结构后其存在的像差也相应被确定。因此需要引入多个变量来控制像差，同时实现特定的畸变值。将球面转变为非球面，引入多个高阶非球面系数，通过求解、优化非球面，使单透镜在满足透镜物像关系的同时实现特定的畸变值。

利用Zemax软件将所得的透镜初始结构参数作为初始值，使用默认优化函数，并在其中加入相对畸变作为目标参数，对透镜的面形参数进行非球面优化，得到透镜面形的非球面表达式：

式中：Z为曲面沿光轴的偏移量；r为透镜表面曲率半径；R为透镜表面半口径；K为二次曲面系数；A2、A4、A6、A8分别为二阶、四阶、六阶和八阶系数。

3 仿真分析

通过Zemax软件对透镜进行仿真优化。透镜的材料选用H-Qk1，焦距为14.24 mm，物距为25 mm，像距为25.5 mm，物高为20 mm，像高为27.66 mm。

设置透镜初始参数，使用默认优化函数，同时在评价函数中加入畸变优化函数“DIST”，优化函数的目标值设置为8%，权重值设置为10。将透镜的曲率半径、透镜厚度、透镜前后表面的非球面系数设置为变量进行优化求解。

优化后的透镜参数如表1所示，非球面透镜的畸变值如表2所示，非球面透镜的残余像差系数如表3所示。

表1 非球面透镜结构参数Table 1 Structure parameters of aspheric lens

表2 非球面透镜畸变值Table 2 Distortion values of aspheric lens

表3 非球面透镜残余像差系数值Table 3 Residual aberration coefficients of aspheric lens

透镜的几何像畸变如图5所示。物面光斑直径相等的线阵激光光斑经过透镜后，在像面处形成中心光斑直径小、边缘光斑直径大的非均匀分布线阵激光光斑。

将图5中的透镜与阿贝棱镜组合，当阿贝棱镜不产生旋转时，像面的线阵光斑与物面入射的线阵光斑方向一致，如图6（a）所示。当阿贝棱镜旋转45°时，像面的光斑绕中心旋转90°，如图6（b）所示。

图5 非球面透镜成像畸变Fig.5 Imaging distortion of aspheric lens

图6 仿人眼扫描系统仿真Fig.6 Simulation of retina-like scanning system

4 结论

本文提出了一种基于透镜畸变实现扫描环增长，并利用棱镜旋转实现对目标视场扫描的仿人眼扫描方法。通过透镜自身的畸变实现对不同视场下入射光斑的放大，形成非均匀线阵仿人眼光斑，利用阿贝棱镜旋转引起出射的非均匀线阵仿人眼光斑旋转的特性，实现对目标区域的仿人眼扫描。通过对仿人眼扫描系统建模，仿真结果表明，本文方法可以实现对目标区域的仿人眼扫描，相比于传统仿人眼扫描方式，本文方法结构简单、制造成本低，同时能够提高仿人眼扫描的速度与扫描精度，为仿人眼扫描的研究与应用提供了一种可行的方案。