机载红外设备多平台协同探测无源定位方法

骆明伟，檀立刚

（四川九洲电器集团有限责任公司 技术创新中心，四川 绵阳 621000）

引言

典型的机载红外侦察设备一般具备红外、可见光和激光等传感器，但在实际使用过程中发现，可见光探测器受云、雨、雾天气影响严重，激光探测器受大气传输衰减限制较大，在远距离或超远距离探测时，可见光成像和激光测距的效果并不理想，红外探测器较前两者受大气环境与复杂背景影响相对较小，出现了激光测距与红外成像作用距离不匹配问题，无法获取激光测距信息[1]。多个不同空间位置分布的机载红外侦察设备，可同时获取多条平台到目标的空间射线，利用空间射线交汇原理，经过空间坐标转、多平台被动测距和目标定位解算等步骤，获取超远距离目标的经度、纬度和高度。在典型多平台协同探测场景下设置多平台参数对多平台协同探测目标定位算法进行仿真验证，若多个平台的目标观测来自于同一个目标，多条空间射线交点即为目标所在位置，可实现目标定位。

相较于传统雷达设备而言，红外传感器为被动探测机制，不容易暴露；相较于声呐、电子支援措施（ESM）设备而言，红外传感器具有明显的测角优势，因此，红外传感器更适合于无源定位领域。无源定位主要有测向定位、到达时差（TDOA）定位、多普勒及其变化率定位、相位差及其变化率定位以及各种方法的复合定位。传统到达方向（DOA）定位测向精度低、定位时间较长、精度较差；TDOA和FDOA不仅需要多机协同完成，还要求较高的时间精度及一定的时延；多普勒及其变化率与相位差及其变化率定位虽然能实现单机高精度定位，但需专用设备且对单机设备测量精度要求较高。

本文研究的多平台协同探测无源定位算法实质上属于多站无源交叉定位，针对无线电静默情形下，如何利用多平台红外侦察设备进行协同探测侦察，实现远距离或超远距离红外目标的无源定位，具有重大而深远的研究意义[2-4]。

1 多平台协同探测无源定位原理

1.1 多平台无源定位建模

多平台无源定位实质上属于多站无源交叉定位，暂不考虑多平台观测数据因数据链传输到达定位融合中心的时延，多平台观测数据不同步以及时间对齐问题可通过定位融合中心时间校准加以解决。远距离或超远距离目标探测，将目标视为质点，且已被红外设备检测到。

假设N个平台同时获取目标的N组有效观测信息，N个平台与目标可构成N条空间射线，若所有观测均来自同一个目标，忽略量测误差时，N条空间射线必然交汇于目标位置[5-6]，空间射线交汇示意图如图1所示。

图1 空间射线交汇示意图Fig.1 Schematic diagram of space rays convergence

在笛卡尔坐标系下，设k时刻平台i(i=1,···,N)的坐标为 (xi,yi,zi) ，目标的坐标为 (x,y,z)，目标相对于平台i的方位角为 αi，俯仰角为 βi，则平台i与目标构成的空间射线方程为

每条空间射线可获得2个独立方程，N条空间射线可获得2N个独立方程，联立并求解方程组，若方程组的秩不小于3，则方程组有解，目标存在且位置唯一。

1.2 空间坐标转换

多平台无源定位建模在笛卡尔坐标系中，在不考虑平台姿态角和红外侦察设备安装影响时，目标相对于平台的方位角和俯仰角即为红外侦察设备给出的方位角和俯仰角，但实际中对于远距离红外侦察，平台姿态角和红外侦察设备安装影响不可忽略，需通过空间坐标转换将平台位置、目标位置和观测角信息统一到空间大地直角坐标系中[7-8]。

1.3 被动测距

多平台被动红外测距主要通过测向交叉定位原理，多个机载红外侦察设备同一时刻测得同一目标的高精度测向线，通过计算各测向线在空间中的交点来确定目标的位置[9]。

假设平台A、平台B和平台C的大地直角坐标系坐标分别为(x1,y1,z1)、(x2,y2,z2)、(x3,y3,z3),目 标O的大地直角坐标系坐标为(x,y,z)（未知待求），与目标O的距离为R1、R2、R3（未知待求），在某一时刻，目标O在平台A、平台B和平台C红外侦察设备本地极坐标系的方位角和俯仰角分别为(a1,e1)、(a2,e2)、(a3,e3)，平台A、平台B和平台C瞬时姿态角（方位角、俯仰角、横滚角）分别为 (θ1,ε1,γ1)、(θ2,ε2,γ2)、(θ3,ε3,γ3)，多平台被动测距转化为如何确定R1、R2、R3，多平台定位转化为如何确定目标O的坐标(x,y,z)。

首先假设3条射线相交于O点，即3个平台同时看到了目标并获取了目标观测信息，实际远距离红外侦察环境中，目标和平台均可看做质点，可得距离方程：

对于平台A而言，β1为在大地直角（ECEF）坐标系中目标O相对于平台A的等效俯仰角，α1为在ECEF坐标系中目标O相对于平台A的等效方位角，可经坐标转换获取。

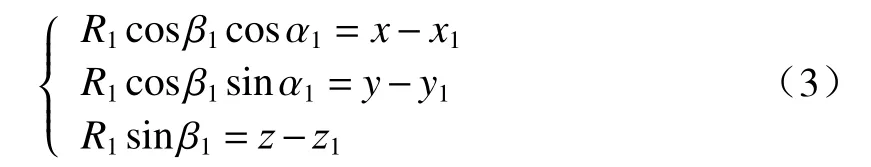
对于平台B而言，β2为在ECEF坐标系中目标O相对于平台B的等效俯仰角，α2为在ECEF坐标系中目标O相对于平台B的等效方位角，也可经坐标转换获取。

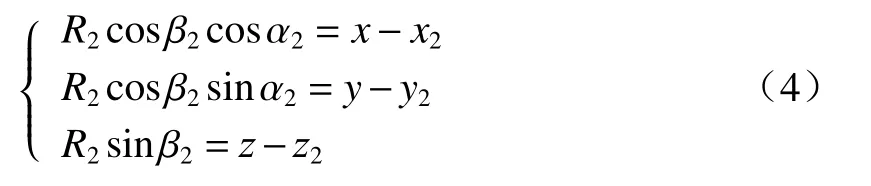
对于平台C而言，β3为在ECEF坐标系中目标O相对于平台C的等效俯仰角，α3为在ECEF坐标系中目标O相对于平台C的等效方位角，同样可经坐标转换获取。

求解（2）式～（5）式联立的方程组即可求得目标相对于平台A、平台B和平台C的距离。

1.4 定位解算

定位过程即目标相对于框架坐标系的位置(α,β,R)和目标在望远镜坐标系中相应像点的位置(xt,yt,f)已 知时，求解目标大地坐标(B,L,H)的过程[10]。

在求解目标位置时，多平台被动测距可获取目标与3个平台之间的距离信息，每个平台通过目标定位过程均可求解出目标的位置信息。无误差时目标位置应完全一致，但由于观测误差的存在，3个平台分别计算得到的目标位置可能不相同，若3个位置距离在允许范围之内，即可认为是同一目标，也可采用滤波算法进一步优化目标位置。

2 仿真试验及数据分析

2.1 仿真试验数据与定位结果

多平台协同探测无源定位参数设置时需要结合场景要求、多平台与目标几何关系、平台姿态角估计和目标观测数据估计等因素综合考虑进行参数设置，以确保多平台无源定位有解，定位误差采用蒙特卡洛方法进行统计分析[11-14]。

设定三平台参数如下：单位（°，m），平台A位置[125.153543.78354000]，平台B位置[125.3535 43.88357000]，平台C位置[125.453543.9835 10000]，平台A姿态角[ 000]，平台B姿态角[ 000]，平台C姿态角[ 000]，平台A观测信息[ 1.5−37.6]，平台B观测信息 [−0.45−40]，平台C观测信息[−1.56−33]，减震器振动角、竖轴倾斜角、脱靶量和焦距等参数不变。

平台A、平台B、平台C和目标的相对位置关系如图2所示。目标与平台A、平台B和平台C 之间距离与误差估计如图3和图4所示。

图2 目标与三平台位置分布关系Fig.2 Position distribution relationship between target and three platforms

图3 目标与三平台之间距离及误差值Fig.3 Distances and errors between target and three platforms

从图3和图4可以看出，平台A与平台B之间距离为19.79 km，平台B和平台C之间距离为14.05 km，平台A与平台C之间距离为33.37 km，多平台被动测距求得的目标与平台A、平台B和平台C之间的距离分别为112.14 km、109.05 km和104.62 km，对应误差分别为7.26 km、7.40 km和7.38 km，距离误差占比分别为6.47%、6.79%和7.0%，若以距离误差为目标定位精度评价标准，定位误差约为7%R，蒙特卡洛仿真计算（10 000次）耗时0.62 s。

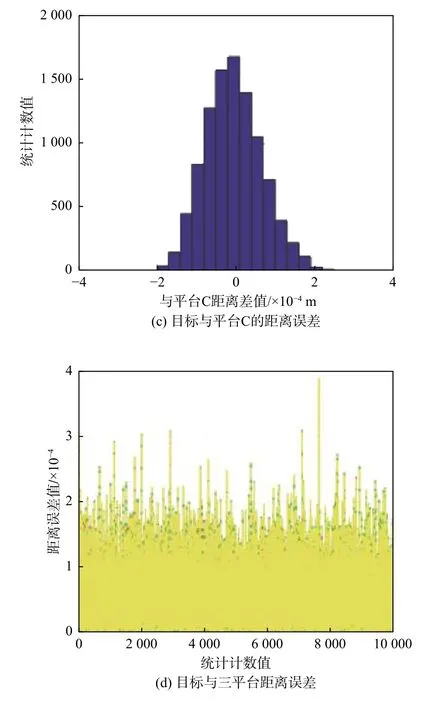
图4 距离误差统计分布情况Fig.4 Statistical distribution of distance errors

利用三平台的测距结果进行目标位置的解算，求取目标的位置信息和误差分布，如图5和图6所示。

图5 目标位置及误差值Fig.5 Target position and errors

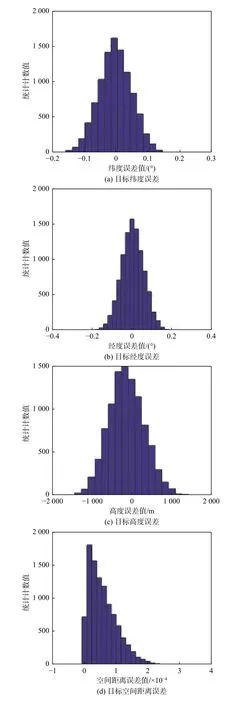
图6 位置误差统计分布Fig.6 Statistical distribution of position errors

目标的大地坐标分别为经度126.169°、纬度44.633°、高度8 019 m，误差分别为0.051 7°、0.055 5°和383 m，折算后目标位置误差为7.59 km，定位精度为7.59%，蒙特卡洛仿真计算（10 000次）耗时0.70 s。

设待引导平台参数如图7所示。

图7 引导平台参数Fig.7 Parameters of guiding platform

使待引导平台指向目标，引导结果及误差如图5（右侧）和图8所示。

目标相对于待引导平台（平台D）的方位角、俯仰角和距离分别为−35.403 9°、1.42°、116.095 km，对应误差分别为2.27°、0.31°和5.80 km。从引导结果上看，方位角和俯仰角均在定位参数设置范围之内，且引导平台位置信息位于三平台经、纬、高之间，目标距离与多平台被动测距结果相一致，俯仰角误差可以接受，方位角误差较大，这与多平台被动测距和定位解算等步骤误差的叠加有关，即与经纬度定位误差有关，arcsin（5/100）/π×180=2.86°，这也一定程度上间接证明了多平台无源定位算法的正确性。

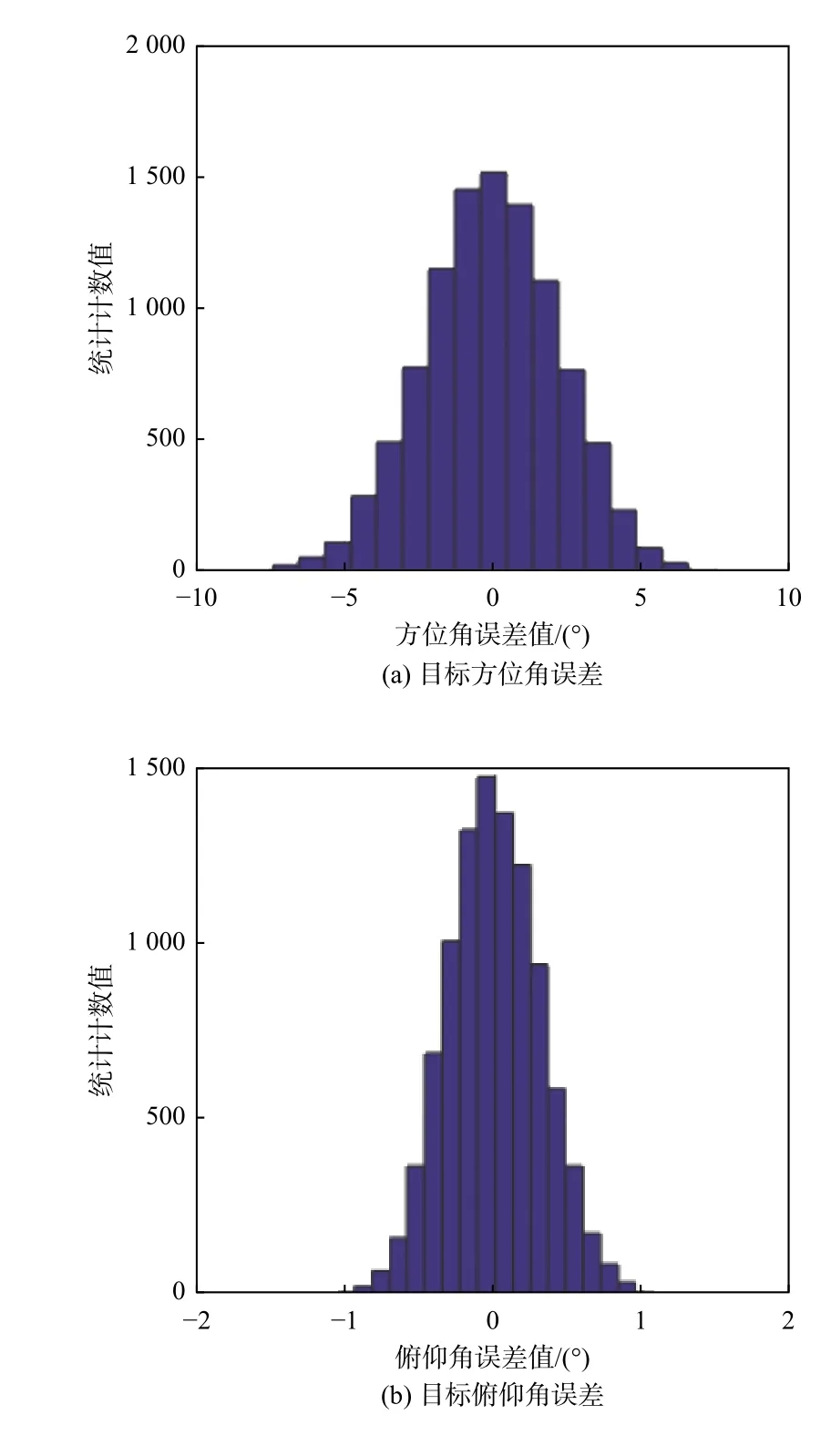
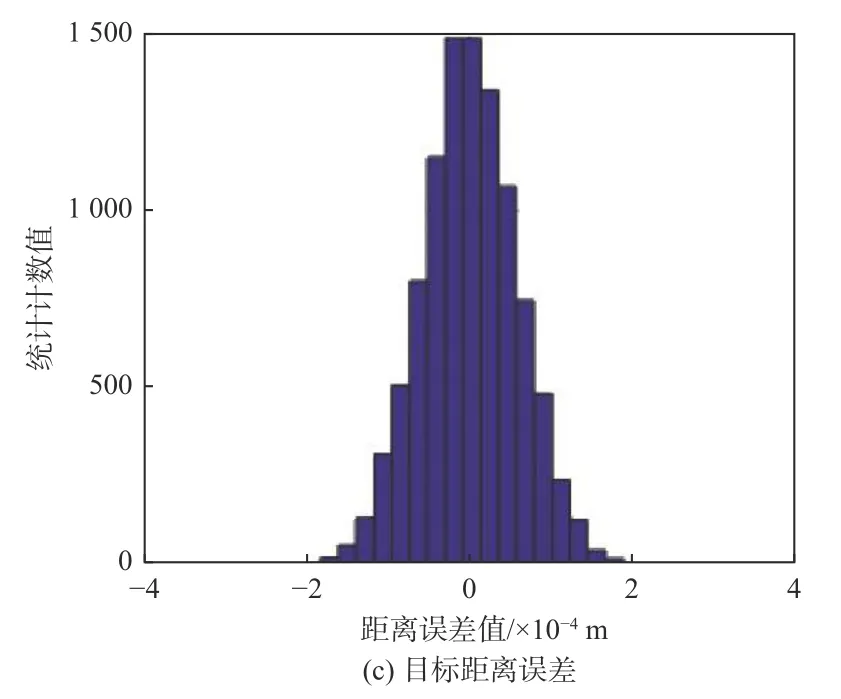
图8 引导误差分布Fig.8 Distribution of guiding errors

2.2 多平台无源定位影响分析

因在实际多平台协同红外侦察场景中，平台位置、平台姿态角、目标观测角等定位参数均实时获取，决定了定位时刻目标与多平台构成的空间几何关系。因每个平台有8个定位输入参数，各参数值对目标与多平台之间的空间几何关系均有影响，由于篇幅限制，不再一一罗列各参数对多平台无源定位的影响程度，仅给出相应的结论与建议[15-16]：

1）平台俯仰角和横滚角增加，被动测距误差和定位误差增大，大于±3°时，不再满足多平台无源定位场景；

2）平台方位角增加或减小，被动测距距离减小或增加，约每变化1°，距离变化10 km；

3）目标与三平台构成等边三棱锥时，为最优定位阵形，定位精度最高，约3%R；

4）满足多平台无源定位条件时，观测角绝对值越大，观测误差引起的影响越小，定位精度越高；

5）可实现多平台无源定位最少平台数目为2个，但并非每次多平台无源定位都能获得可接受结果。

6）为进一步提高目标定位精度，建议采用高精度测量设备，并尽可能保持最优阵形进行多次多平台无源定位。

3 结论

本文提出了一种基于机载光电设备的多平台协同探测无源定位方法，设计了多平台无源定位软件，实现了远距离或超远距离目标高精度定位，可应用于不同场景无距离信息条件下多平台无源定位，满足大多数场合定位精度要求。

虽然基于机载光电设备的多平台协同探测无源定位方法可实现较高精度的目标定位，但是多平台之间互引导、目标与多平台瞬时空间几何关系持续变化及非最优、多平台观测数据有效性与时间不同步等问题仍有待进一步深入研究。