快速反射镜挠性支承运动学设计

王大志，樊 越

（1.中国科学院 光电技术研究所，四川 成都 610209；2.成都大学 机械工程学院，四川 成都 610106）

引言

快速反射镜是一种具有高响应速度的可动反射镜，它通常与主跟踪架结合构成大动态范围、高精度的跟踪系统，是复合轴光电跟踪设备的重要部件。挠性支承是快速反射镜的关键部件，主要用于负载反射镜，并约束其运动，以获得工作所需自由度。挠性支承具有零间隙、免润滑以及响应速度快等优点，近年来在快速反射镜中得到逐步应用[1-5]。

目前，快速反射镜的挠性支承具有多种结构形式，但缺乏相关对比分析，对其运动学性能有待进一步认识，并且现有设计主要依赖工程师的直觉和经验，缺乏严格的理论基础，容易导致错误。此外，现有挠性支承构型是否完备，是否还有其他可能的支承形式可供选择，这些均是总体设计中需要回答的问题。

运动学原理主要研究物体的约束、自由度及其相互关系[6-7]。运动学设计可以理解为运动学原理在机械设计中的应用，它注重以最少的约束数目和正确的约束方式限制零件的运动，使其具有需要的自由度。符合这种原则的机械结构具有运动确定、重复精度高以及元件变形小等优点，如运动学轴系、运动学联接以及精密调平机构等[8-10]。本文主要从运动学角度研究快速反射镜挠性支承的设计问题，旨在建立快速反射镜挠性支承的完备构型和系统认识，为快速反射镜的选型、优化和工程设计提供指导和依据。

1 约束与自由度

一个自由物体在空间具有6个自由度，包括3个平动自由度和3个转动自由度。物体的运动受到限制，则由“自由状态”变为“非自由状态”。对物体的运动产生限制作用的其他物体，称为约束物体，简称为约束，约束物体对被约束物体的作用力，称为约束力。它通过物体之间的相互接触产生，其作用点为两物体的接触点，方向沿接触点的公法线指向被约束物体。

约束力可以采用节距为零的旋量，即线矢量W表示为

式中：f表示约束力的大小；sw是约束力的单位方向矢量；rw是约束力的位置矢量。

自由度是指物体具有的独立运动，可以采用运动旋量 δΦ表示

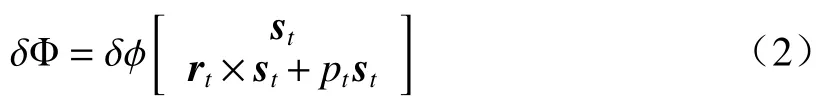
式中：δφ表 示运动旋量的大小；st为运动旋量的方向矢量；rt为运动旋量的位置矢量；pt为运动旋量的节距。

约束力的作用线称为约束线，自由度旋量的轴线称为自由度线，如图1所示。

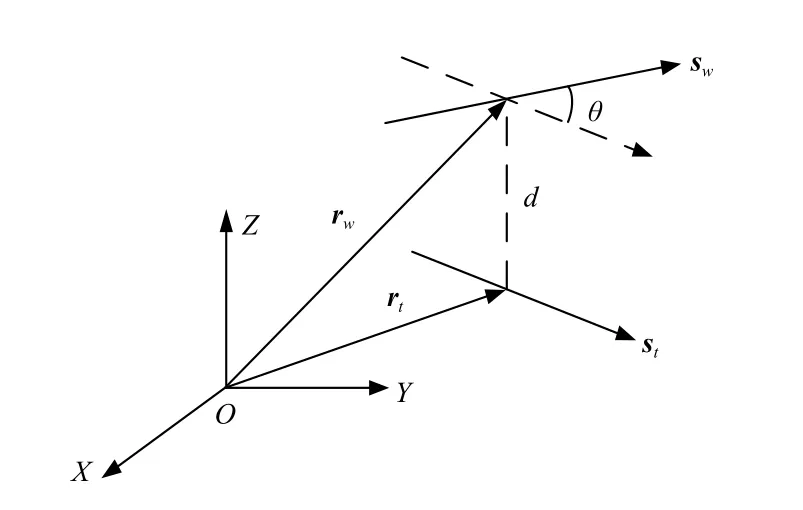
图1 约束线与自由度线Fig.1 Constraint line and degree of freedom line

根据约束力W与自由度 δΦ的互易积为零[11-15]，则有：

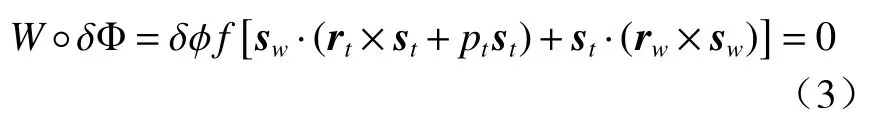
式中“°”表示旋量互易积的运算符号。

整理（3）式可得：

式中：θ表示约束线和自由度线的夹角；d表示约束线和自由度线的公垂线段长度。

根据（4）式可知，物体的约束线与自由度线满足如下空间位置关系：

1）约束线与转动自由度线相交（包括相交、平行或重合）；

2）约束线与平动自由度线垂直（相交垂直或异面垂直）；

3）约束线与螺旋自由度线垂直相交或异面。

已知物体自由度线的数目F和非冗余约束线的数目C满足F+C=6，按照约束线与自由度线的空间位置关系，给定物体的自由度线，即可确定物体的约束线，反之亦然。

约束线的空间分布表示物体的约束模式，将这些约束线用约束元件代替，即可得到一种机构构型。运动学设计就是通过合理配置约束数目和分布方式获得需要的物体自由度。由于约束和自由度概念的一般性，它对机构设计具有普遍的指导意义。

2 反射镜的约束模式

如图2所示，快速反射镜主要包括基座、反射镜、镜框、音圈电机以及挠性支承等。它通过相对的2个音圈电机以推拉的方式驱动反射镜绕两轴线转动。

图2 快速反射镜结构示意图Fig.2 Structure diagram of fast steering mirror

按照光的反射定律，反射光线的方向随反射面法线方向的变化而变化，反射面的法线可以通过2个参数确定，这样通过反射镜的2个转动就可以调整其法线在空间的指向，进而实现光束的指向控制。因此，快速反射镜的挠性支承应具有2个相交的转动自由度R1和R2。

根据约束线与自由度线的空间位置关系，反射镜的转动自由度线均与约束线相交，据此可以确定反射镜的约束模型，包括一个约束球CS和一个约束平面CP。约束球CS由所有过球心的约束线构成，约束平面CP由平面上不全互相平行的约束线构成，如图3所示。

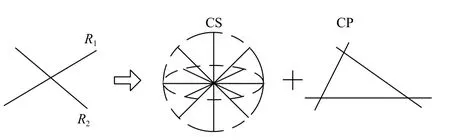
图3 反射镜的约束模式Fig.3 Constraint pattern of mirror

约束球CS的球心与自由度R1、R2的交点重合，则CS上的每条约束线与R1、R2相交，约束平面CP与R1、R2确定的平面重合，则CP上的每一条约束线与R1和R2相交，从而使R1、R2与CS和CP中的约束线均相交。

快速反射镜的自由度数F=2，可对它施加4个非冗余约束，则CS和CP中的任意4条非冗余约束线均可作为快速反射镜的一种约束模式。快速反射镜挠性支承的运动学设计本质上就是通过配置4条非冗余约束线，使反射镜具有2个转动自由度。

3 挠性支承构型

细杆是具有较大长径比的杆件，在轴向具有良好的刚性，而在其他方向具有良好的挠性。它具有结构简单、便于加工的优点，可作为提供纯力约束的机械元件，利用其刚柔二元特点可构造不同类型的快速反射镜挠性支承。如图4所示，细杆的一端与基座B固定，另一端与物体A固联。

图4 细杆Fig.4 Slender rod

物体A沿Z向的平动自由度通过细杆消除，仅具有沿X向和Y向的2个平动自由度以及绕X轴、Y轴和Z轴的3个转动自由度。因此，细杆在轴向可以看作是刚性的，在横向可以看作是挠性的。它提供一条沿杆件轴线方向的纯力约束线，对与其固连的物体施加一个纯力约束Ci（用标记符号Ci且两端带圆点的线段表示约束线）。

如上所述，快速反射镜的约束模型是一个约束球CS和一个约束平面CP，其中任意4条非冗余约束线均可作为反射镜的一种约束模式，一共具有4种不同的约束模式，对应4种不同构型的挠性支承。

构型1。从CS球中取出1条约束线C1，且C1不在CP平面上，再从CP平面上取出3条约束线C2、C3、C4，且C2、C3、C4不在CS球上，如图5所示。这4条约束线C1、C2、C3、C4是反射镜的第1种约束模式，据此配置细杆可得反射镜挠性支承的第1种构型，如图6所示。

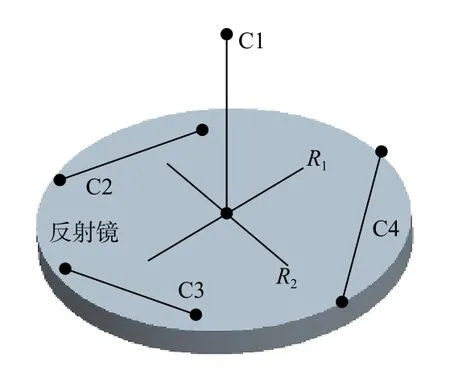
图5 第1种约束模式Fig.5 Constraint pattern 1

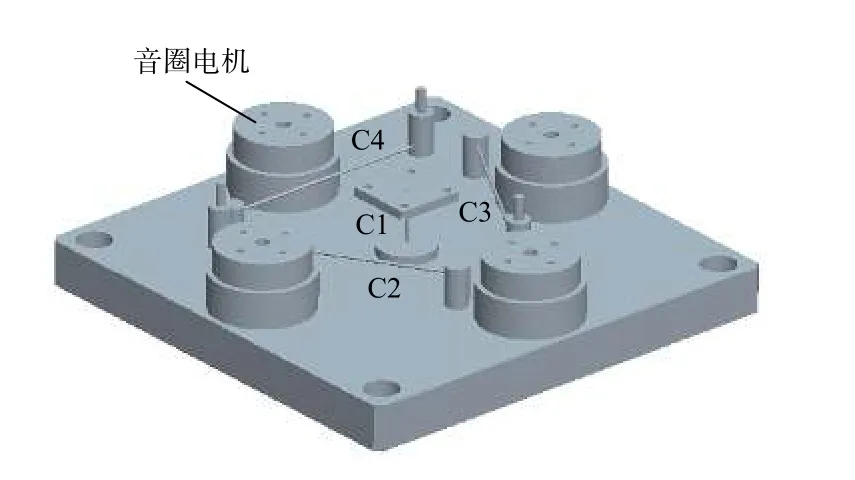
图6 第1种构型Fig.6 Configuration 1

构型2。从CS球中取出3条约束线C1、C2、C3，且C1、C2、C3不在CP平面上，再从CP平面中取出1条约束线C4，且C4不过CS球的球心。这4条约束线C1、C2、C3、C4是反射镜的第2种约束模式，如图7所示。图8所示为反射镜挠性支承的第2种构型，其中C5、C6是为实现结构对称添加的冗余约束，C5在CS中选取，C6在CP中选取。

图7 第2种约束模式Fig.7 Constraint pattern 2

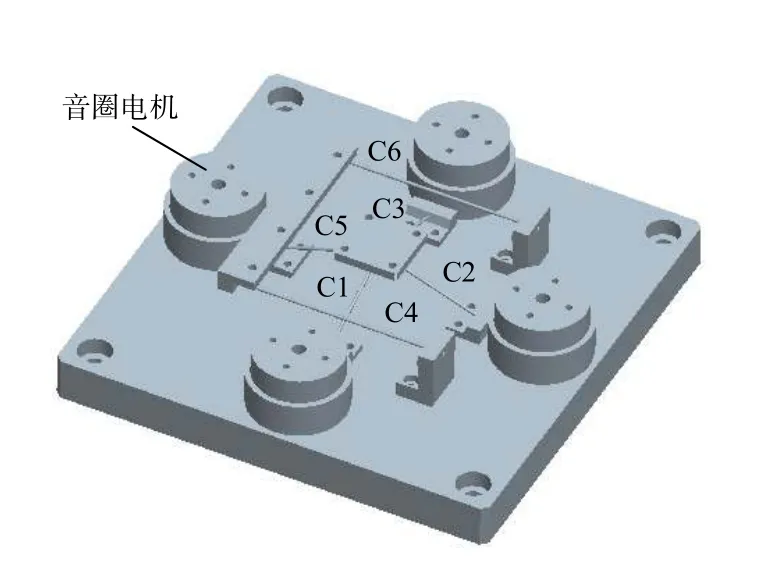
图8 第2种构型Fig.8 Configuration 2

构型3。从CS球中取出两条约束线C1、C2，且C1、C2不在CP平面上，再从CP平面上取出两条相交的约束线C3、C4，且C3、C4均不通过CS球的球心。这4条约束线C1、C2、C3、C4是反射镜的第3种约束模式，如图9所示。据此配置细杆可得反射镜挠性支承的第3种构型，如图10所示，其中C5、C6是冗余约束，用于保证结构对称。

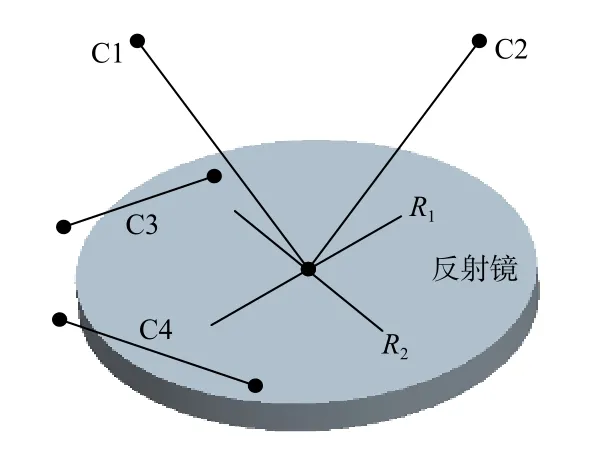
图9 第3种约束模式Fig.9 Constraint pattern 3

图10 第3种构型Fig.10 Configuration 3

构型4。从CS球中取出两条约束线C1、C2，且C1、C2不在CP平面上，再从CP平面上取出两条平行的约束线C3、C4，且C3、C4均不通过CS球的球心。这4条约束线C1、C2、C3、C4是反射镜的第4种约束模式，如图11所示，据此配置细杆可得反射镜挠性支承的第4种构型，如图12所示。

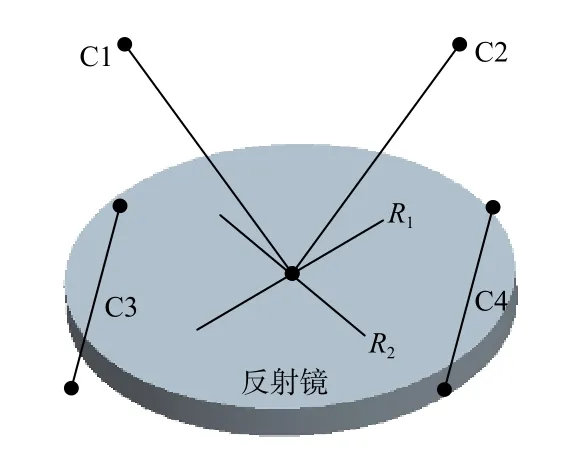
图11 第4种约束模式Fig.11 Constraint pattern 4

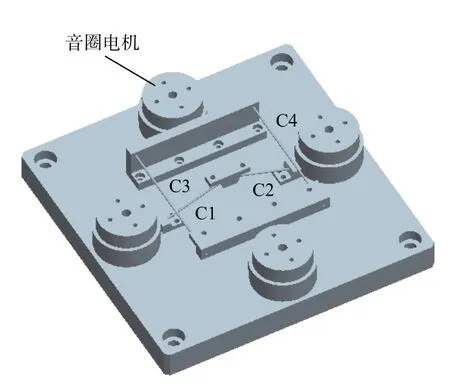
图12 第4种构型Fig.12 Configuration 4

这4种约束模式均包括4条约束线。第1种约束模式按轴向1个约束和侧向3个约束分布，第2种约束模式反之，轴向3个约束，侧向1个约束。相对而言，第1种构型承受侧向负载的能力较强，而承受轴向载荷的能力较弱。第3、4种约束模式在轴向和侧面均具有两条约束线，承受轴向负载和侧向负载的能力适中。在实际设计中，需要根据它们的力学特点，选择合理的约束模式和构型。此外，第1、4种构型不存在欠约束和过约束，易于获得较高的重复精度，并具有装配简单、环境适应性强的优点。第2、3种构型为保证结构对称性增加了冗余约束，对零件的加工和装配精度要求更高。

4 结论

运动学是机构具有良好性能的必要条件，也是进行机构动力学分析与控制的基础。本文以细杆为约束元件构造了反射镜挠性支承的4种完备构型，提供了快速反射镜机构设计的运动学基础，为统一认识各种挠性支承结构形式提供了理论依据。例如文献[1]所述快速反射镜属于第1种构型，文献[2]所述快速反射镜属于第2种构型（利用球面副提供3个相交约束），第3和第4种构型尚未见有文献报道，是获得的新型挠性支承。文献[3]～[5]所述快速反射镜采用柔性铰链，不属于细杆支承，故不作讨论。

本文属于概念设计范畴，旨在建立机构正确的运动学，以此为基础可以进行后续工程结构设计和动态性能分析等，推进机构的实用化。