双模功率分流混动系统的扭振问题主动控制研究

徐德锋 张建武 于海生

(上海交通大学机械与动力工程学院，上海 200240)

0 引言

本文混合动力系统为双模功率分流型式，由行星齿轮系统而构成的功率分流装置具备两个运动自由度。内燃机与两副驱动电机的功率耦合使得混合动力系统的动力学特性十分复杂：动力传递过程并非沿着单一路径单一方向传递，而是具有多个路径选择，并且能够实现双向传递，特别是电功率循环问题。复杂的动力传递过程使得混合动力系统对扭矩冲击更加敏感，在机械系统薄弱处更容易引发异常的传动系统扭转振动问题。此外，混合动力系统为实现更高的能量利用效率，摒弃了液力变矩器，不利于衰减和隔绝来自内燃机的扭矩冲击。

在控制架构上，混合动力系统的模式切换过程控制遵循两个既定目标：其一，能量管理策略会实时根据当前车辆状态和驾驶员油门踏板开度，估计整车功率需求，在附加考虑动力电池功率需求的前提下，获得内燃机最优工作区间，指示内燃机输出功率稳定跟踪总和功率需求；其二，动态扭矩分配策略则会根据内燃机运行状态，计算驱动电机的扭矩需求，分配杠杆扭矩，调整杠杆姿态，将内燃机调整和维持在最优工作区间内。而在剧烈驾驶工况下，剧烈变动的内燃机输出功率极易造成动态扭矩分配策略的巨大误差，使得杠杆姿态调整和扭矩平衡的功能失效，并容易在控制环路中不断强化，从而引起传动系统剧烈且持续的异常扭转振动[1]。此外，离合器扭矩切换、内燃机脉动扭矩和其他不确定性因素都可能引入扭矩冲击，破坏动态扭矩分配功能，造成异常扭转振动问题。

因此，如何增强混合动力系统的模式切换控制稳定性和可靠性，有效避免异常扭转振动的发生和强化，主动抑制和衰减已经发生的异常扭转振动，将是本文的核心研究内容。

学者在机械系统扭转振动响应机理方面进行了广泛而深入的研究工作，其中唐小林等[2-5]采用传递函数模型和ADAMS软件分析方法综合研究了某款功率分流混合动力系统的扭转振动机理，采用传动系统固有特性调优方法能够解决车辆在纯电驱动模式向混动驱动模式切换过程中的振动噪音问题。然而机械结构优化方法在系统研发后期面临更多制约因素，介入成本更高昂。

基于驱动电机的扭转振动主动控制则提供了更加直接高效的介入途径。国内外学者的相关研究主要集中在前馈控制和反馈控制两方面。前馈控制主要使用滤波器方法，常用的滤波器类型为陷波滤波器和双二阶滤波器[6-7]。前馈控制主要从输出扭矩需求或者内燃机输出功率估计等方面入手，滤除机械系统固有频率上的控制分量[8]。反馈控制则更多地纳入对模型参数不确定性和未建模动力学的设计，常用方法有LQR[9-10]、μ设计方法[11]、加速度反馈[12]和频域设计[13]等方法。前馈控制更加简单，但会造成扭矩响应滞后和整车加速性能下降等问题，而反馈控制则对控制频率要求更严苛，整体控制效果更好。

本文将混合动力系统的模式切换控制模型简化为双弹簧耦合系统，区别于前人研究中的双质量弹性系统，系统自由度更高，控制难度更大。采用鲁棒控制方法，将复杂的模型不确定性和未建模动力学纳入到控制器设计中，推导出反馈增益的优化算法。利用龙贝格观测器的转速和扭转角估计结果，与动态扭矩分配策略的控制参考值形成跟踪误差，采用鲁棒反馈能够有效避免和抑制传动系统扭转振动，提高杠杆姿态调整和扭矩平衡的稳定性和可靠性。

1 扭转振动控制问题描述

1.1 混合动力系统构造

混合动力系统的结构如图1所示，系统配备有内燃机、两副驱动电机、4副离合器、双排单行星齿轮系统、行星排主减速器、差速器、传动半轴和车轮等，其中双排单行星齿轮系统通过CR-CR连接方式构成的功率分流装置属于四轴杠杆机构。

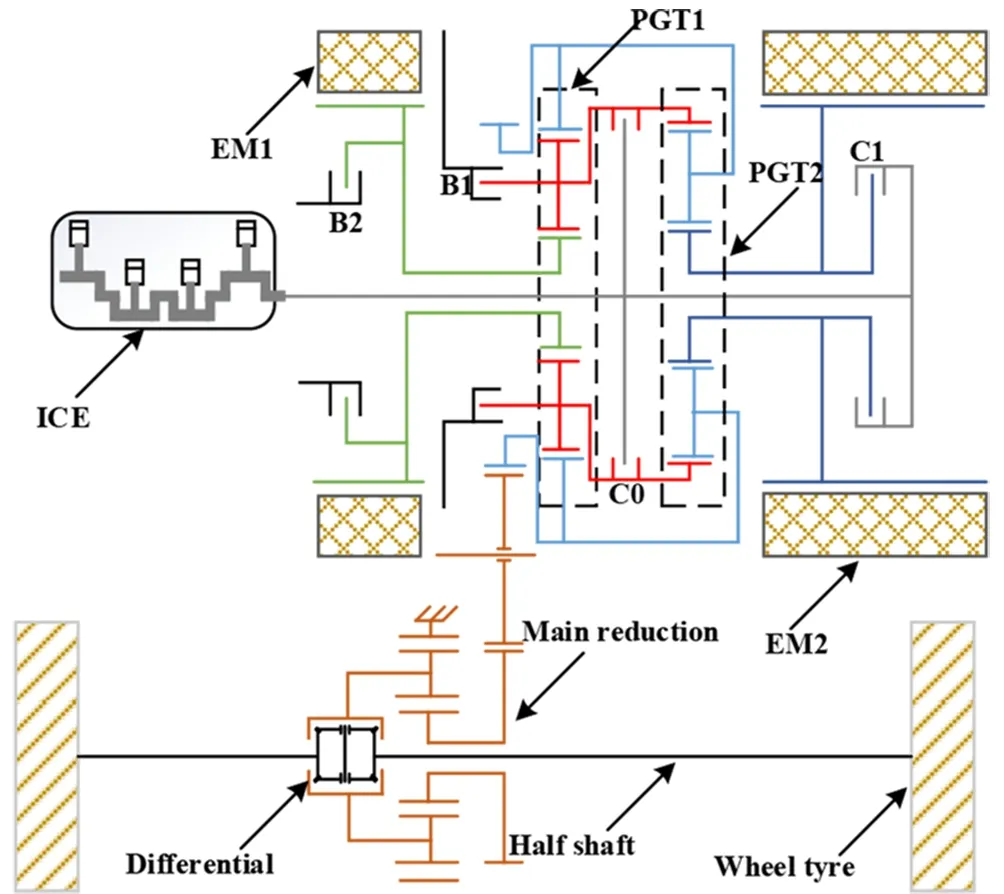
图1 双模功率分流混合动力系统构型Fig.1 Structure of the dual-mode power-split system

内燃机的输入扭矩在经过扭转减振器之后，可以选择通过离合器C0或者C1分别传递到功率分流装置的C1R2(行星排PGT1的行星架与行星排PGT2的齿圈)或者PGS2(行星排PGT2的太阳轮)。与此同时，驱动电机EM1通过PGS1(行星排PGT1的太阳轮)输入扭矩，驱动电机EM2则通过PGS2输入扭矩。三者输入的扭矩在功率分流装置的耦合作用下再将输出扭矩经过R1C2(行星排PGT1的齿圈和行星排PGT2的行星架)传递到主减速齿轮副，在第三排减速行星排和差速器的作用下最终驱动车辆行驶。

1.2 模式切换过程

选取混合动力系统的两个典型功率分流驱动模式之间的切换过程作为控制策略的验证对象。应用等效杠杆原理[14]，将混动系统驱动模式可视化，如图2所示。仅有离合器C0或C1锁止，则分别形成功率分流模式。切换过程中，采用纯电动模式作为过渡。

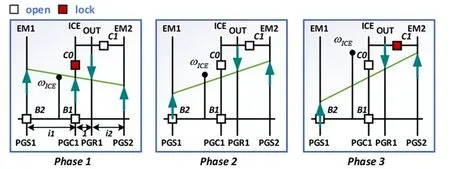
图2 两个功率分流模式之间的切换过程Fig.2 Transition process between two power-split drive modes

1.3 道路实车试验数据分析

道路实车试验中采集到与功率分流模式相关的异常扭振现象，如图3和4所示。

图3离合器C0打开瞬间，杠杆转速和整车车速都发生剧烈波动。离合器C0完全打开后，内燃机扭矩也调整到60 N·m以下，而转速则飞升到2 200 r/min以上。当离合器C1两端的转速差在500 r/min以上时，离合器C1闭合，内燃机转速被急剧下拽至1 900 r/min左右，并经历约0.5 s才完成与PGS2的转速同步。传动系统扭转振动发生在C0打开瞬间，并在C1闭合时恶化。整个扭转振动过程持续1.5 s以上，整车车速出现1.5 km/h以上的上下波动。

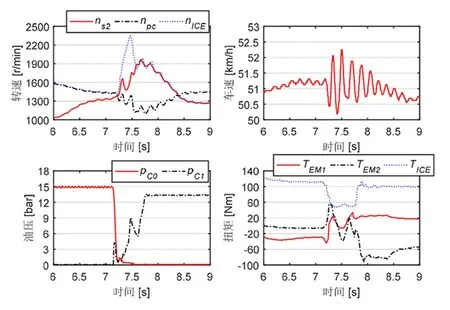
图3 异常扭振案例1

图4中出现相似的扭转振动情况，并且在离合器C0打开瞬间，PGS2和PGC1的转速差反而扩大300 r/min以上，与杠杆姿态调整预期相悖，表明动态扭矩分配策略在杠杆姿态调整上出现失效情况。

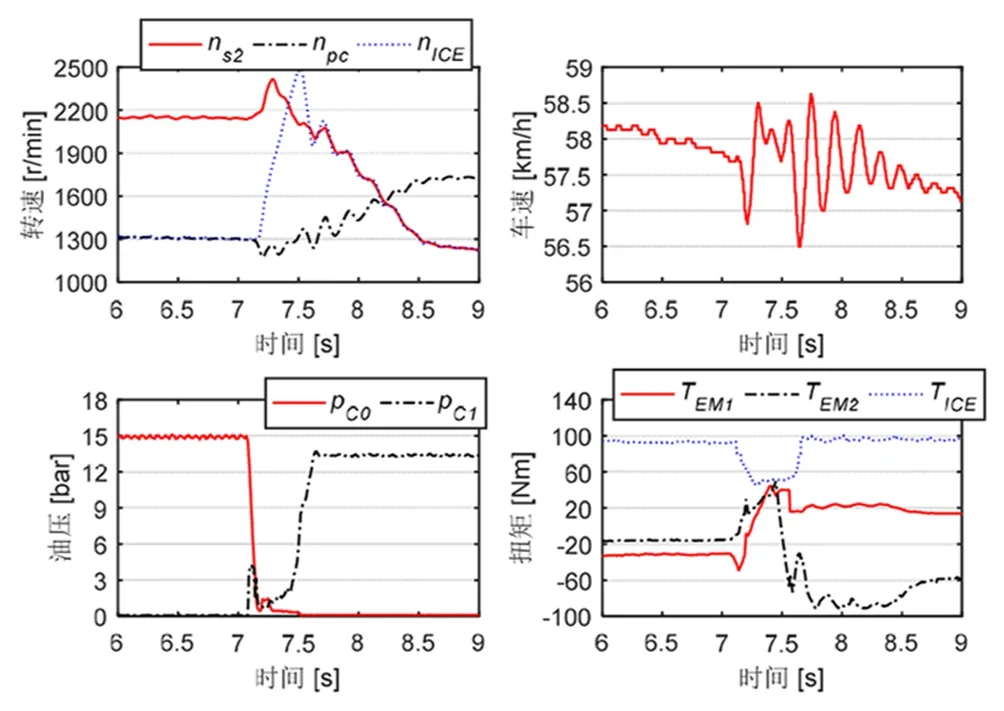
图4 异常扭振案例2

由此可知，离合器和内燃机的剧烈扭矩控制，导致了传动系统恶劣的扭转振动。整车车速出现大幅度且持续的波动，极易传导至驾乘人员，恶化驾驶平顺性和驾乘舒适性。扭转振动过程最初发生在离合器C0打开瞬间，单靠离合器C1的滑动摩擦控制并不能覆盖全部时段，也无法有效解决其他扭矩冲击引起的扭转振动问题。此外，动态扭矩分配策略出现杠杆姿态调整失效的问题。

2 混动系统数值仿真模型

本文采用LMS/AMESim搭建混合动力系统的数值仿真模型，用于验证控制策略。由于内燃机扭矩被视为引起扭振问题的重要因素之一，本文增加了内燃机脉动扭矩的建模和验证过程，而系统其他部分建模与验证可参考之前研究[15]。

图5为脉动扭矩模型的计算结构，其中ω为内燃机转速，θ为内燃机转角。

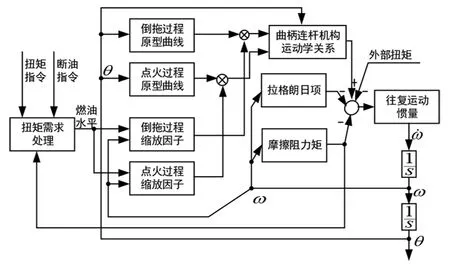
图5 内燃机脉动扭矩数值计算模型

首先，扭矩脉动模型接收来自于混合动力控制单元(Hybrid Control Unit，HCU)的扭矩指令和断油指令。若断油指令为1，则内燃机进入倒拖工况；若为0，则内燃机进入点火工况。在点火工况中，扭矩指令将被换算为燃油水平。换算依据不同转速和燃油水平下的缸压曲线和平均有效制动压力(Brake Mean Efficient Pressure, BMEP)的对应关系。

然后，由于四冲程工作循环的缸压曲线是无法通过理论分析得到精确解析解，因而从缸压试验数据中选取具有代表性的内燃机倒拖工况和点火工况下的关于曲轴转角的缸压模板曲线，而不同的燃油水平和转速下的缸压曲线由缸压模板曲线和尺度因子相乘而得。尺度因子根据燃油水平与曲轴转速查表得到。

其次，采用理论分析推导了曲柄连杆机构的动力学特性和运动学约束、曲轴等效惯量和惯性扭矩。摩擦阻力矩的来源和影响因素虽然复杂，但扭矩相对较小，因而忽略其他复杂因素的影响，利用在倒拖试验中获得的摩擦阻力矩与倒拖转速的拟合关系曲线来表示摩擦阻力矩。

最后，惯性扭矩中的拉格朗日项、气体作用扭矩、摩擦阻力矩和外部扭矩叠加作用于等效转动惯量上，产生曲轴转角加速度、曲轴转速和转角，并最终回到模型的计算过程中构成闭环。

内燃机采用双质量简化模型，得到单缸曲柄连杆机构中曲柄转角与活塞行程的运动学关系为：

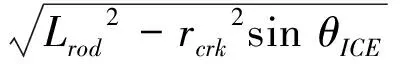
(1)

式中，Spst为活塞行程，Bcld为活塞有效直径，Lrod为连杆长度，rcrk为曲柄半径，θICE为曲柄转角。

四冲程直列四缸内燃机，按照1-3-4-2点火次序，得到气体作用扭矩为：

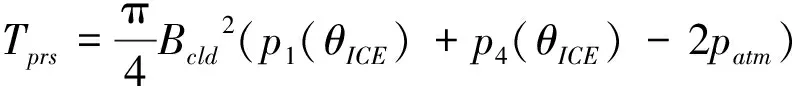
(2)

式中，Tprs为气体作用扭矩，patm为大气压力，pi为单缸的缸压，i=1,2,3,4。

图6将几个测点工况的实际缸压曲线和模型预测曲线做了对比。倒拖工况的缸压峰值出现在压缩行程的上止点，而点火工况的缸压峰值要稍微延后，出现在点火爆燃时刻。整体而言，模型预测和试验数据在峰值和曲线形状上很契合，缸压计算模型的精度已经足够满足控制策略验证的需求。

图6 试验结果与模型预测的缸压曲线比较

从能量守恒定律出发，可以得到内燃机等效转动惯量为：

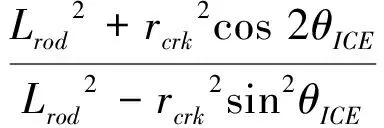
(3)

式中，Jcrk为曲柄的转动惯量，mpst为活塞的质量。

将曲柄转角设为广义坐标，采用拉格朗日第二类方程，得到惯性扭矩为：

(4)

本文采用倒拖试验获得的阻力矩与倒拖转速的二次拟合关系来建立摩擦阻力矩模型[16]。

3 扭转振动系统主动控制策略

3.1 扭振系统控制模型

通常将传动系统简化为双质量模型，如图7(a)所示。双质量模型由两个质量元件和一个弹性阻尼元件构成。两个质量元件分别表示变速箱内部惯量和整车等效惯量。在仅有单一动力传递路径的传动系统中，弹性阻尼元件的刚度和阻尼特性是由扭转减振器、液力变矩器、驱动轴和轮胎等部件的特性等效而来。

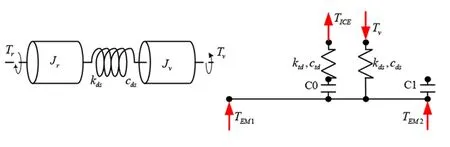
(a) 双质量模型 (b) 双弹簧耦合模型图7 传动系统简化模型Fig.7 Simplified models of transmission systems

当前混合动力系统具备两个运动自由度，多条动力传递路径，混合动力系统被简化为双弹簧耦合模型，如图7(b)所示。混合动力系统的弹性和阻尼集中等效到扭转减振器和驱动轴处，形成两个弹性阻尼元件。两个元件的一端共同连接着功率分流装置，而另一端分别连接着内燃机和整车。由于离合器的存在，使得扭转减振器处弹性阻尼元件可以随着离合器切换而与功率分流装置的不同位置连接。

以当前的双弹簧耦合模型为基础，可以将混合动力系统的主动控制过程按照图2中模式切换过程划分为三个阶段，采用分阶段控制。

3.2 主动控制系统架构

主动控制系统架构如图8所示，包含模式切换状态控制、动态扭矩分配策略、龙贝格观测器和鲁棒反馈控制器。

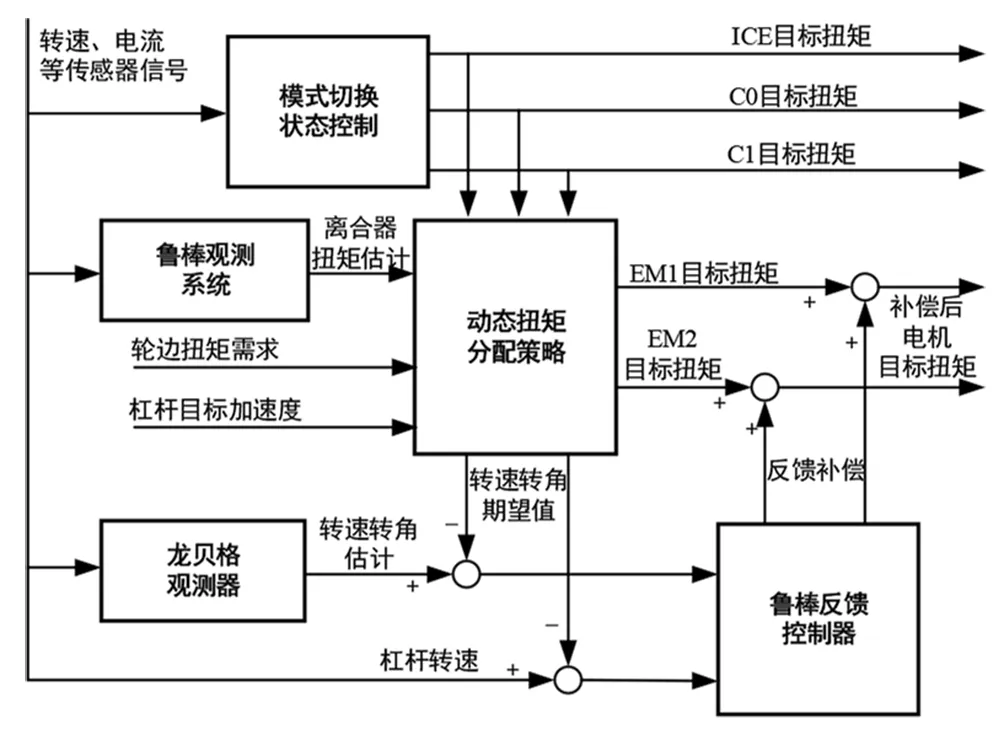
图8 主动控制系统架构

模式切换状态控制基于杠杆姿态等信息，采用时序和状态逻辑来确定内燃机和离合器的目标扭矩。

动态扭矩分配策略属于前馈控制环节，以当前轮边扭矩需求和杠杆目标加速度为锚定，配合鲁棒观测系统提供的离合器扭矩估计结果[17-18]，以杠杆扭矩平衡和转速约束关系解算出系统目标转速、驱动电机目标扭矩和系统内部扭矩；并且结合扭转减振器和驱动轴的刚度阻尼特性，解算出扭转角度期望。

当前混合动力系统仅能获得内燃机、驱动电机和轮边转速测量信号，而轮边转速测量信号主要用于防抱死制动系统(Anti-lock Braking System, ABS)，测量精度无法达到扭转振动主动控制要求。为此需设计龙贝格观测器来获取扭转角和轮边转速的估计结果。

鲁棒反馈控制器将双弹簧耦合系统的转速和扭转角作为反馈变量，其中扭转角被纳入到反馈设计是有利于稳定扭转角度来衰减扭转振动的。

3.3 基于转速和扭转角跟踪的鲁棒反馈控制

鲁棒控制方法能够将控制问题中的闭环误差与控制输入两项纳入到性能优化指标中，并与传动系统受到的外界参数摄动、不确定性干扰和未建模动力学等未知因素建立关联。选取内燃机转速、扭转减振器扭转角度、PGC1或PGS2转速、PGR1转速、驱动轴扭转角度和驱动轮转速为状态变量，得到控制模型的状态空间表达式为：

(5)

以第一阶段为例，其中：

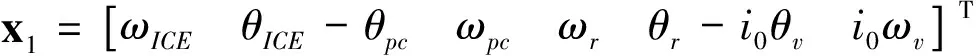
(6)

按照控制周期离散化，可以得到：

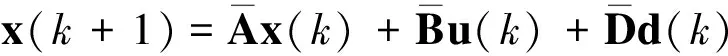
(7)

状态反馈控制律为：

u(k)=Ke(k)

(8)

式中e(k)=x(k)-r(k)为跟踪误差，K为反馈增益，r(k)为状态变量期望值。

离散系统的误差状态空间表达为：

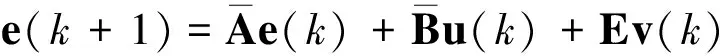
(9)

式中矩阵与系统扰动分别为：

(10)

采用如下目标函数：

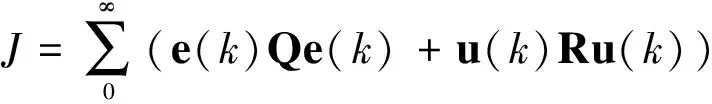
(11)

式中矩阵Q和R分别表示误差权重系数和输入权重系数。

将目标函数改写为二次型，则控制输出定义为：

z(k)=Mξ(k)+Nu(k)

(12)

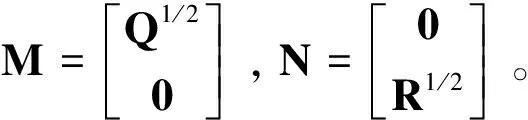
依照性能指标：

(13)

可以得到闭环方程：

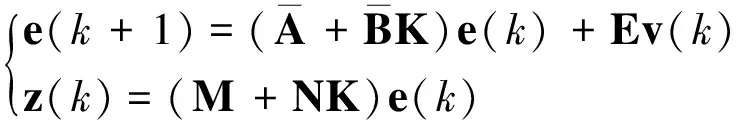
(14)

在零状态初始条件下，鲁棒控制的目标函数往往还需考虑李雅普诺夫函数的终值。因此建立如下与目标函数梯度相关的函数：

Φ(k)=V(k+1)-V(k)+
zT(k)z(k)-γ2vT(k)v(k)

(15)

利用杨氏不等式，可以得到满足式(13)的充分必要条件为式(15)小于零。由于控制输出与系统扰动相互独立，利用舒尔补定理[19]，将不等式条件转化为线性矩阵不等式：

(16)

其中，H=KP-1,Γ=P-1，K=HΛ-1为最优反馈增益，P为李雅普诺夫函数正定对称阵，。

4 测试工况与结果分析

4.1 测试工况设置

以车速和驱动轴扭矩为变量，不改变能量管理策略预定的内燃机最优工作转速、扭矩和杠杆目标加速度，设置了两个测试工况：

(1)低速工况：车速60 km/h时进行驱动模式切换，驱动轴扭矩为763 N·m；

(2)高速工况：车速90 km/h时进行驱动模式切换，驱动轴扭矩为801 N·m。

为体现一致性，将驱动模式切换前后的内燃机扭矩设置为120 N·m，转速设置为1 400 r/min。

在低速和高速工况设置下，设置三种控制情况，形成相互对照：

(1)无反馈控制工况：控制系统内不包含反馈控制，仅采用动态扭矩分配策略来进行前馈控制，有助于重现扭转振动情况；

(2)鲁棒反馈控制工况：控制系统采用鲁棒反馈控制器进行反馈控制，用于验证扭转振动主动控制的有效性和性能表现；

(3)LQR反馈控制工况：控制系统采用LQR反馈控制器进行反馈控制，与鲁棒控制器形成对照组，有助于辨别控制系统在外部扰动和不确定性影响下的控制性能优劣。

4.2 主动控制结果分析

图9、图10和图11分别为三种控制情况下低速工况测试的转速和扭转角跟踪结果。

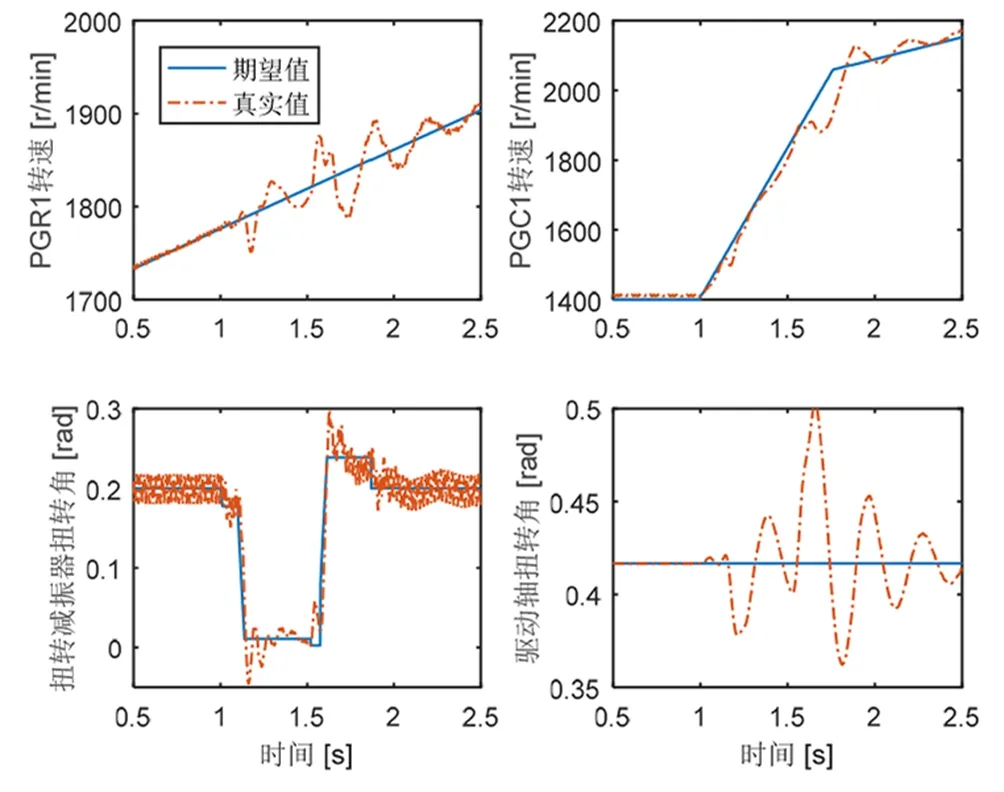
图9 无反馈控制下的转速和扭转角跟踪结果(60 km/h)

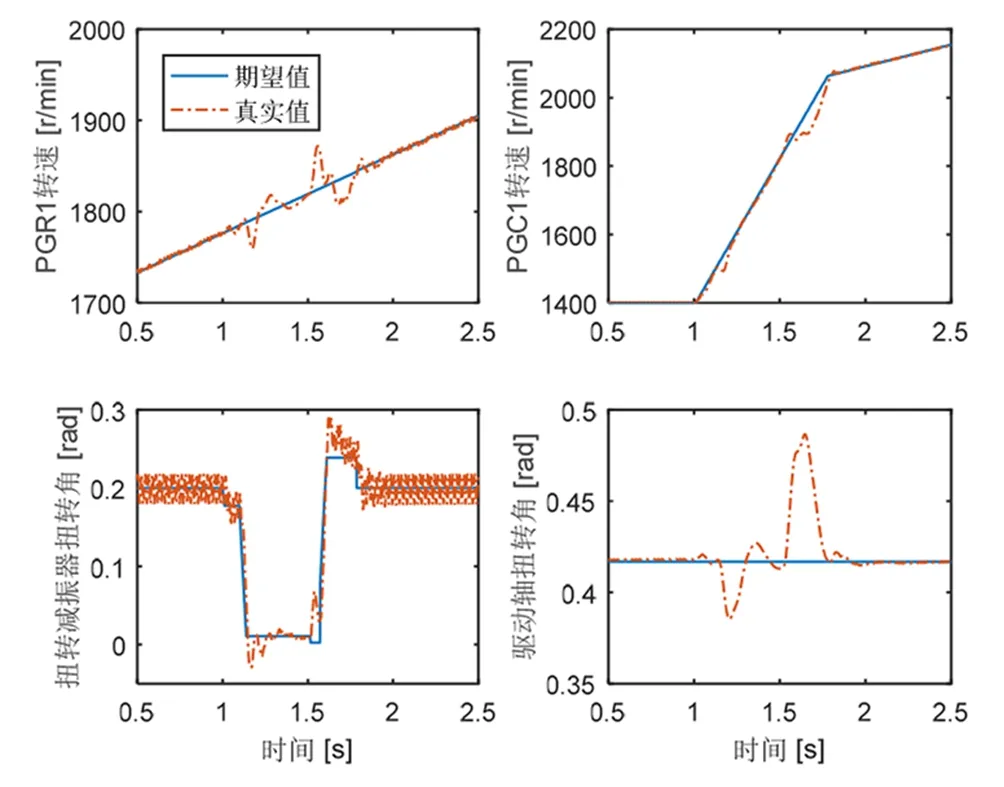
图10 LQR反馈控制下的转速和扭转角跟踪结果(60 km/h)

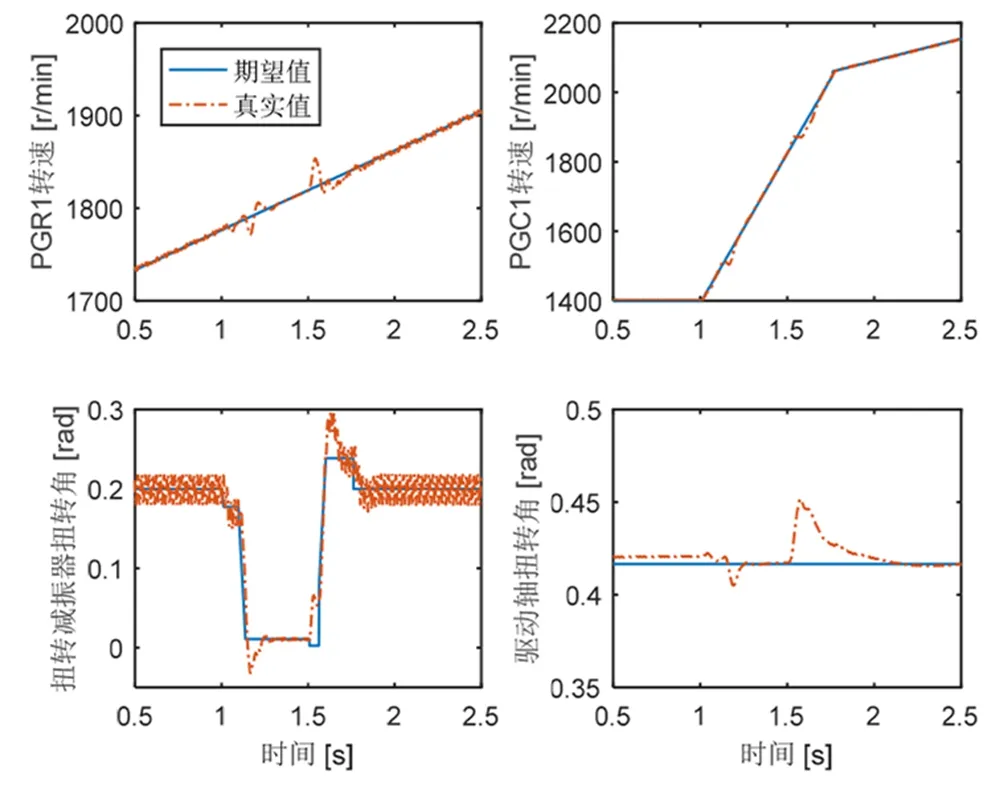
图11 鲁棒反馈控制下的转速和扭转角跟踪结果(60 km/h)

无反馈控制情况下，扭矩冲击造成了转速和转角的跟踪失效，杠杆姿态剧烈抖动。驱动轴转角的剧烈波动表明，扭矩冲击直接传递到驱动轴扭矩，形成整车冲击。

LQR反馈控制情况中，内燃机和离合器引入的扭矩冲击同样引起杠杆姿态的剧烈抖动，并部分传递到整车上。但转速和扭转角很快跟踪上期望值，扭矩冲击引起的扭转振动得到抑制和衰减。

鲁棒反馈控制情况下，转速和扭转角跟踪效果优于LQR反馈控制，扭矩波动引起的扭转振动也更快得到抑制和衰减。转速和扭转角波动幅值小于LQR反馈控制中的幅值。

实际上，内燃机和离合器的扭矩调整过程不仅引入了很强的扭矩冲击，也存在极大的扭矩不确定性(从控制模型角度来说，混合动力系统动力学模型中的内燃机脉动扭矩和离合器扭矩是未知的，属于不确定性)，进而造成两种反馈控制情况下系统响应的巨大差异，从而印证了鲁棒反馈控制的鲁棒性能。

图12为不同控制情况下系统响应和控制变量的结果比较。无反馈控制情况下的驱动轴扭矩波动幅值最大，达到270 N·m左右。LQR反馈控制情况下波动幅值在140 N·m左右。而鲁棒反馈控制情况下波动幅值仅为70 N·m左右，并且模式切换时长缩短0.1 s。

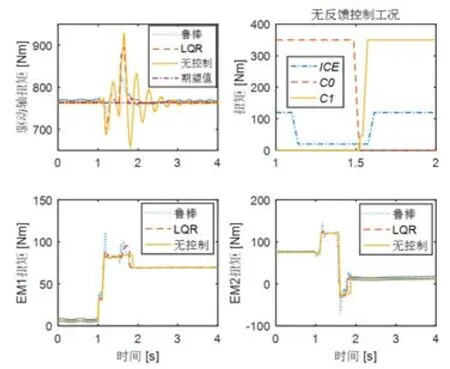
图12 不同情况下系统响应和控制变量的结果比较(60 km/h)

图13为不同情况下高速工况系统响应和控制变量的结果比较。驱动轴扭矩波动幅度在无反馈控制、LQR反馈控制和鲁棒反馈控制情况下分别为150 N·m、120 N·m和70 N·m左右。鲁棒反馈控制在无反馈控制情况的基础上将模式切换持续时间缩短0.1 s左右。

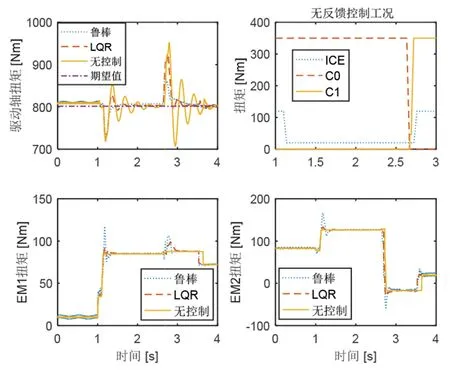
图13 不同情况下系统响应和控制变量的结果比较(90 km/h)

5 结论

本文认为异常扭转振动问题的根源在于三个方面：

(1)摈弃液力变矩器，以扭转减振器和驱动轴的刚度阻尼特性为主的低阻尼特征；

(2)功率分流装置造成的动力传递路径具备不唯一且双向的特征；

(3)驱动模式切换过程的扭矩波动更频繁，幅值更大，具体来源包括离合器扭矩切换、内燃机脉动扭矩和其他不确定性因素。

采用扭振问题主动控制方案，得出如下结果：

(1)将功率分流的耦合特征归纳为双弹簧耦合控制模型，刚度和阻尼特性集中于扭转减振器和驱动轴；

(2)将主动控制结构分为前馈和反馈两部分：动态扭矩分配策略起到前馈作用，响应轮边扭矩需求和杠杆目标加速度，并计算出转速和扭转角的期望值，以及驱动电机目标扭矩；鲁棒反馈控制在转速跟踪的基础上，将扭转角纳入反馈跟踪控制中，更加符合双弹簧耦合模型特性，直接以扭转角来限制扭矩波动幅值。

(3)鲁棒反馈控制的整体性能优于LQR反馈控制，对内燃机和离合器的扭矩不确定性具有一定的鲁棒性能。