一种提升3K型行星轮系传动效率的方法

陶 煜 詹东安 吕 昌 程大海

(江苏汇智高端工程机械创新中心有限公司，江苏 徐州 221000

0 引言

与传统的NGW型行星减速机相比，3K型行星齿轮减速机具有结构更加紧凑、齿数少的情况下可实现大传动比、功率密度高等优点，尤其适用于低速重载工况，在各种特种车辆、工程机械和其他传动系统中得到了广泛的应用，其结构简图如图1所示。3K型行星减速机虽然具有以上诸多优点，但其结构是由一个传统的负号机构与一个正号机构复合而成，故存在功率内循环，传动效率会随着传动比的增大而降低[1]。

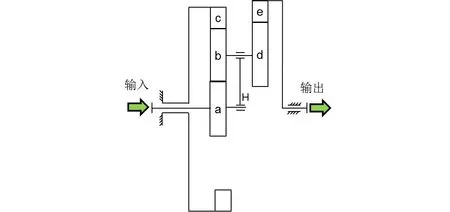
图1 3K型行星齿轮减速机结构简图

Muller[2]在假设单对齿轮副啮合效率为0.975的条件下，计算得出传动比为100的3K型行星减速机的传动效率只有0.546。因此传动效率是衡量3K型行星减速机性能好坏的重要指标，也是限制其进一步推广应用的制约因素。笔者针对上述问题首先分析了行星减速机传动效率的影响因素，进而提出一种低速重载3K型行星减速机的效率提升方法。

1 3K型行星轮系传动效率推导

如输入功率确定，那么功率损失将决定传动效率。行星减速机的功率损失由以下五部分组成：

1)齿轮的啮合损失；

2)轴承的摩擦损失；

3)密封件的摩擦损失；

4)齿轮与行星架的搅油损失；

5)空气阻力损失。

对于工作在低速重载工况下的3K型行星减速机，轴承及密封的摩擦损失、搅油及空阻损失占比极小，决定其传动效率的是齿轮啮合损失。

1.1 结构功能等效分解

3K型行星轮系是一种复合行星轮系，包含3个中心轮、1个行星架及数个行星轮，啮合效率的计算十分复杂。Muller[2]认为任何一种复合行星轮系均可以分解成若干个基本行星轮系，3K型行星轮系根据不同的输入输出组合方式，通过基本行星轮系拥有3种可行的等效传动分解方式，由基本行星轮系I、II、III组合而成，见图2所示。

图2 3K型行星轮系等效分解方式

轮系中任一构件的转矩值(不考虑功率损失)在a、b、c这三种等效传动分解方式下具有相同值。而Kurth[3]指出，只有功能等效分解方式才能真实替代图1的3K型行星轮系，用以计算轮系啮合效率，并且具有相同的运动学与静态特性。图1所示的3K型行星传动简图，功率由太阳轮输入，齿圈c固定，最终由齿圈e输出，其功能等效分解方式对应图2(b)，由基本行星轮系I、III复合而成，图中的齿圈c与c′、齿轮 b与b′完全相同。该3K行星轮系的总传动效率等于基本行星轮系I、III的传动效率乘积，见式(1)。

η3K=ηI·ηIII

(1)

式中：

η3K——图1所示3K行星轮系传动效率

ηI——基本行星轮系I的传动效率

ηIII——基本行星轮系III的传动效率

1.2 基本行星轮系传动效率计算

基本行星轮系I是一个NGW型2K-H简单行星轮系，根据外加力矩平衡条件，中心轮a、c及行星架H上的外加扭矩之和为零，即

∑Ti=Ta+Tc+TH=0

(2)

图3中，如果功率由中心轮a输入，经行星架H输出，中心轮c固定，则此时传动效率

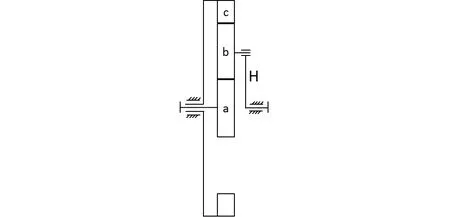
图3 NGW型2K-H简单行星轮系

将式中绝对值符号解除，得

TaωaηaH+THωH=0

可表示为

(3)

同理，如果功率由中心轮a输入，经中心轮c输出，行星架H固定，则此时传动效率

将式中绝对值符号解除，得

可表示为

(4)

将转矩方程(2)与式(3)、(4)联立，得一组关于三个基本构件外加转矩的齐次线性方程，即

(5)

显然，当定轴传动效率η0已知时，为计算该行星传动的效率ηaH，可令式(5)的系数行列式为零，有

(6)

解得：

采用上述方法，可使用定轴轮系传动效率表示基本行星轮系I任意中心轮输入的传动效率，即在各种功率流情况下的传动效率。而的计算如下：

η0=ηabηbcηL

(7)

式中，

ηab——中心轮a与行星轮b间齿轮啮合效率；

ηbc——行星轮b与中心轮c间齿轮啮合效率；

ηL——搅油、空阻、轴承、密封等齿轮啮合外的传动效率。

同理，可使用上述方法推导出II、III轮系在各种功率流情况下的传动效率，整理得

1.3 单对齿轮副啮合效率计算及提升方法

单对齿轮副啮合功率损失是齿轮啮合过程中，齿面间相对滑动造成，Niemann[3]给出了以下的计算方法：

Ploss=Pin·Hv·μm

(8)

式中：

Pin——输入功率

Hv——啮合损失系数

μm——平均摩擦系数

而啮合损失系数Hv可按下式计算(εa<2)：

(9)

式中：

i—— 齿轮传动比

z1——输入齿轮的齿数

β——齿轮螺旋角

εa——端面重合度

ε1——啮合节点前重合度

ε2——啮合节点后重合度

联立式(8)、(9)可得单对齿轮副啮合效率：

η=1-(Hv·μm)

(10)

从式(10)不难看出，可通过减小平均摩擦系数μm、啮合损失系数Hv来提升齿轮副的啮合效率。Wimmer[4]还指出可通过减小重合度、减小齿轮模数、增大压力角、增加小齿轮的齿数来提升齿轮啮合效率。Bernd-Robert[5]更是提出了一种低功率损失齿轮副设计原则：

1)啮合节点处于啮合线中点；

2)通过削顶减小齿顶高，进而减小重合度，使。

下文将在实例中使用Bernd-Robert原则提升齿轮副啮合效率。

1.3 3K型行星减速机传动效率

图2(b)功能等效分解方式中，行星轮系I为太阳轮a输入，行星架H输出，齿圈c固定；行星轮系III为行星架H输入，齿圈e输出，齿圈c′固定。如查表1后可得I、III传动效率如下：

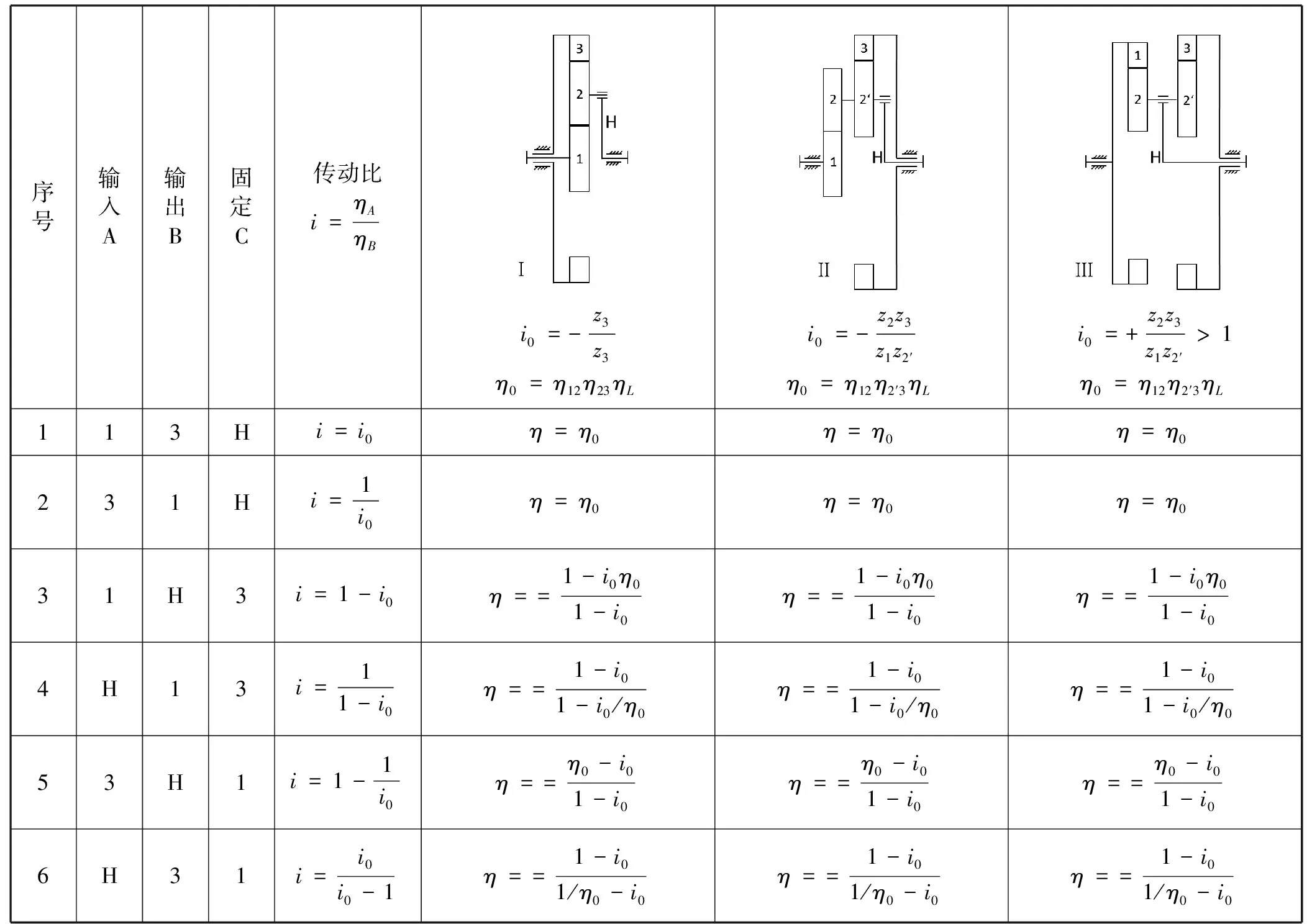
表1 基本行星轮系传动效率

(11)

此时可比较ηI、ηac的大小：

表明行星轮系I的传动效率ηI总是高于对应的定轴传动效率ηac。

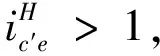
(12)

此时可比较ηIII、ηc′e的大小：

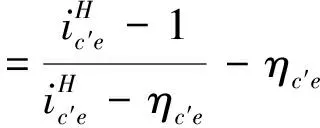
表明行星轮系III的传动效率ηIII总是低于对应的定轴传动效率ηc′e。AGMA6123[1]指出这是因为正号机构存在功率内循环，齿轮啮合传递的功率远大于输入功率所致。

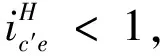
(13)

同样可证明此时ηIII<ηc′e。

(14)

(15)

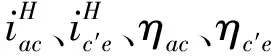
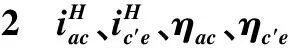
表对η3K的影响

2 效率提升实例

某款工程机械用3K型行星减速机，其传动原理见图1，齿轮副基本参数见表3。在输入转速500 r/min、输入功率30 kW的额定工况下，使用ISO VG220润滑油，台架实测80℃时传动效率为0.832，连续工作温升过快且无法达到热衡，试验台架的布置见图4。

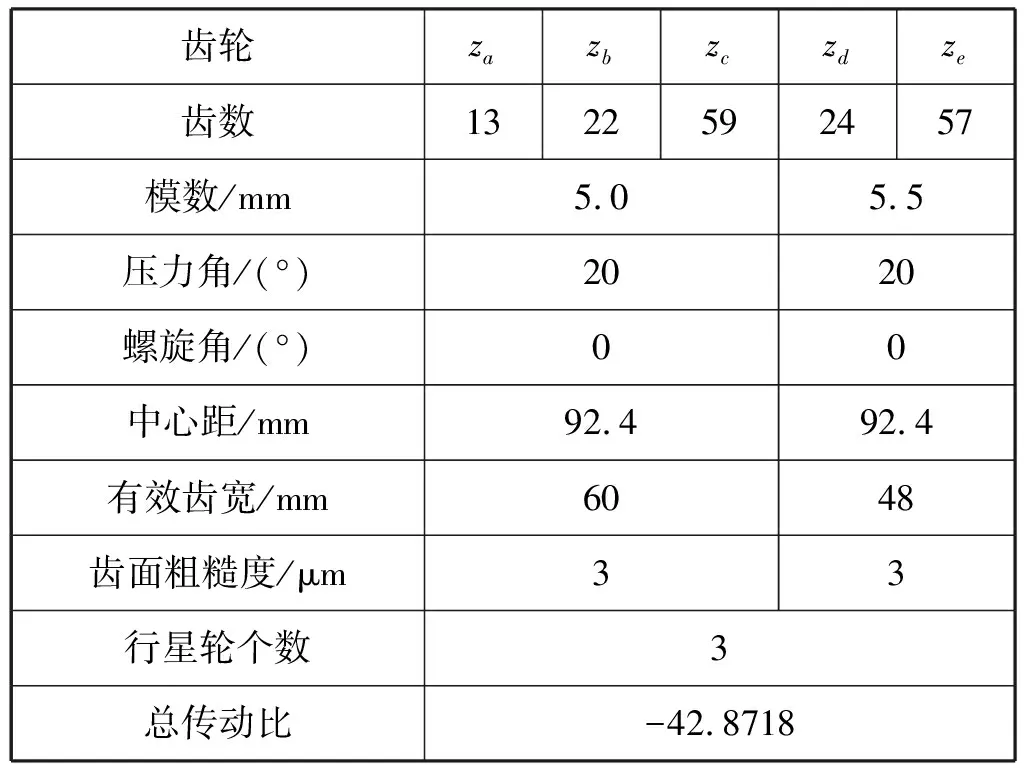
表3 原减速机齿轮副参数

图4 3K型行星轮台架搭建形式

为提升该减速机的传动效率，在径向不增加尺寸，满足3K型行星传动装配条件，保证齿轮安全系数的基础上，减小重合度εa、减小齿轮模数、增大压力角、增加小齿轮的齿数，形成了新的产品方案，该方案的齿轮副基本参数见表4。

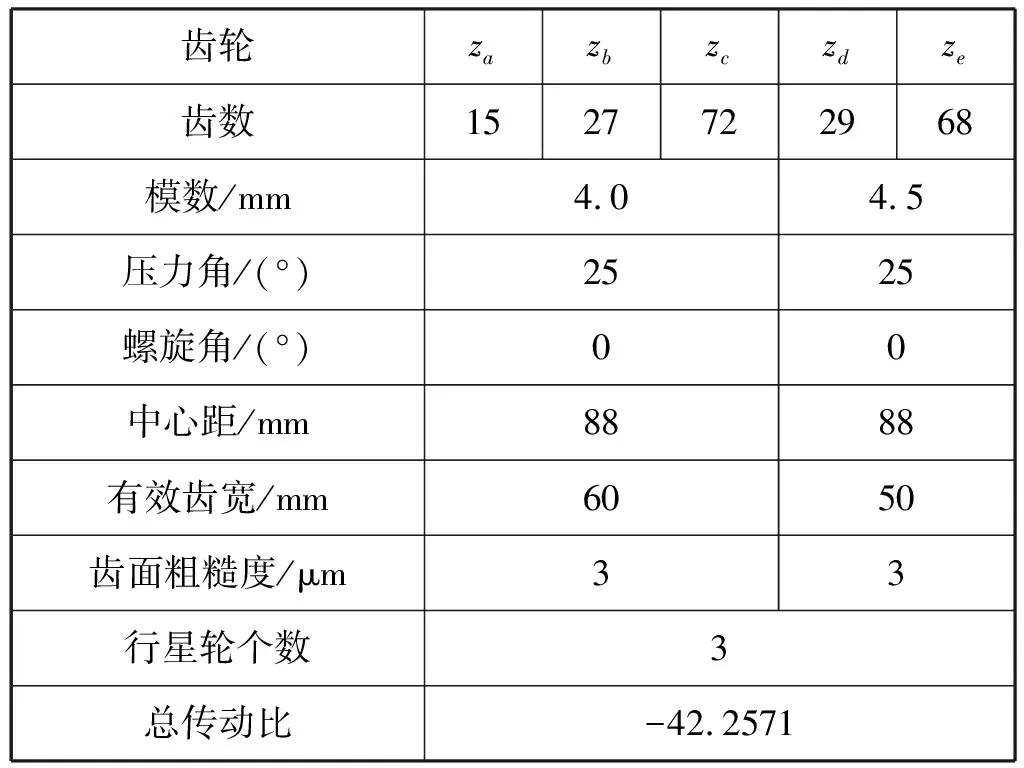
表4 改进后减速机齿轮副参数

使用本文推导的3K型行星轮系传动效率计算方法，在同样运行工况下，计算出改进设计后基本行星轮系I、III的传动效率ηI、ηIII，计算结果见表5、表6。

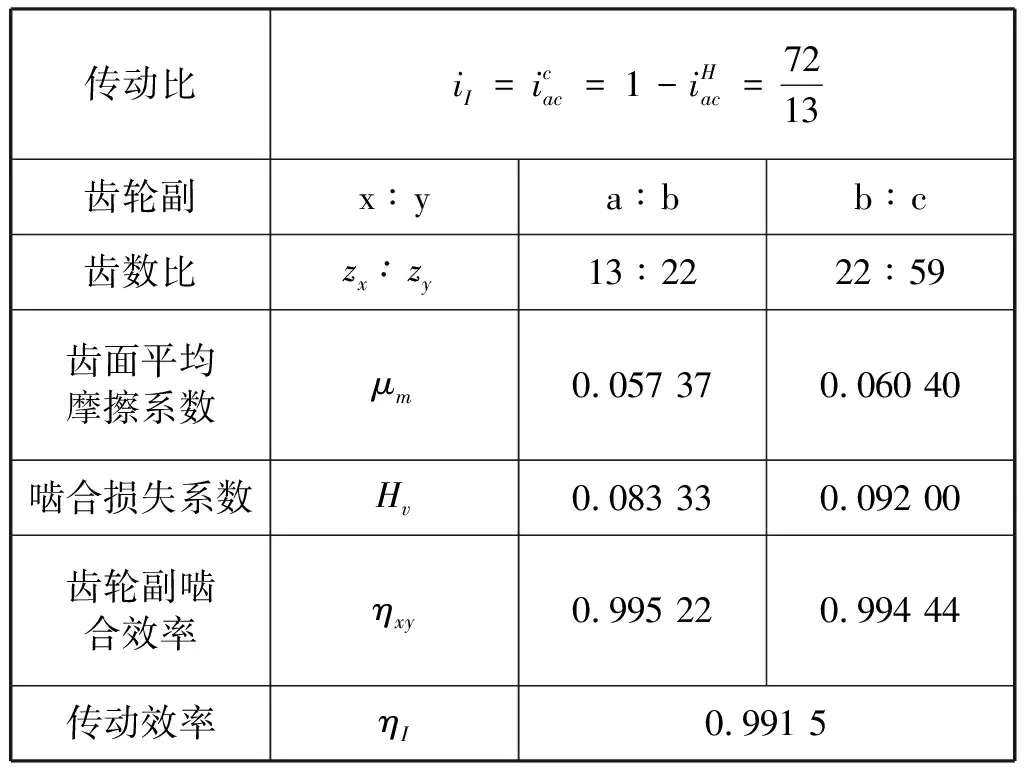
表5 基本行星轮系I、III的传动效率

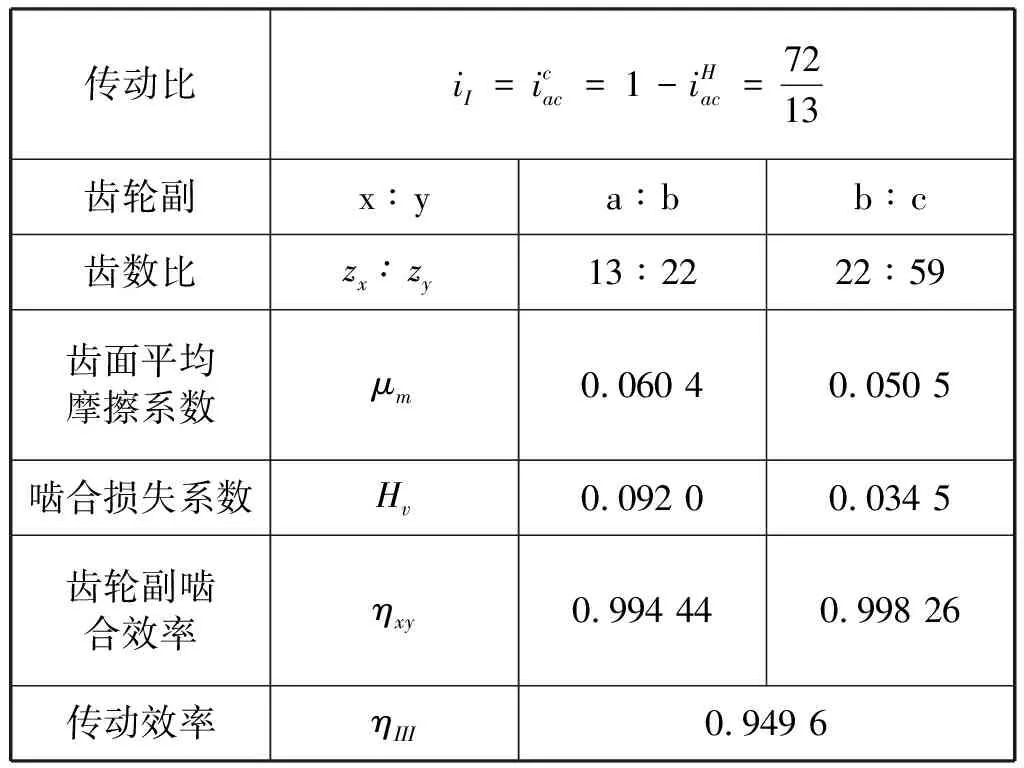
表6 基本行星轮系I、III的传动效率

改进方案后的3K型行星减速机传动效率：

η3K=ηI·ηIII=0.991 5×0.949 6=0.941 5

采用相同的台架搭建形式及测试工况，实测改进后的减速机总体传动效率为0.935，考虑到理论计算时未考虑轴承、密封、搅油功率损失，测试效率值与计算值较为吻合。

3 结论

本文提出了一种3K型行星齿轮减速机的效率计算方法，并根据效率计算公式分析出3K型行星齿轮减速机效率影响因素及效率提升方法，并对某款3K型行星减速机进行了改进设计。改进后计算传动效率由原来的0.820 0提升至0.941 5，实测传动效率提至0.935，效率提升效果显著，计算值与实测值较为吻合。