飞行模拟器经典洗出算法分析与改进

朱道扬 段少丽

(武汉交通职业学院，湖北 武汉 430065)

飞行模拟器的运动平台通常选择性能较理想的六自由度液压平台[1]，然而飞行模拟器的运动空间会受到六自由度液压平台的限制，严重影响飞行模拟器有效复现飞机的真实飞行特性。针对这种情况，研究人员先后提出三种比较成熟的洗出(体感)算法：经典洗出算法[2]、最优控制洗出算法[3]、自适应洗出算法[4]，此外还有众多围绕这三类算法的改进算法[5-6]，其目的是克服运动洗出过程中的问题。国外对洗出算法的改进先后在美国NASA埃姆斯研究中心的运动基模拟器VMS和荷兰代尔夫特理工大学的固定基模拟器SRS 上进行了试验[7]，取得了较好的试验效果。

其中经典洗出算法以其结构简单、执行速度和反馈速度迅速、参数调节容易等优点而被国内外研究及人员所热衷。然而该算法也存在不足，首先是高通平移通道和倾斜协调通道存在耦合现象，倾斜协调通道直接采用低通滤波，虽然可以有效模拟持续加速度的特性，但是也造成了虚假暗示的发生[8]，进而影响飞行模拟器洗出的动感逼真度。郭盛等增加高频低通滤波器和极值限制环节有效解决了算法的稳定性和可靠性[9]，但是无法解决高频以下信号的丢失问题；其次，倾斜协调原理是用重力加速度模拟持续加速度，必然不能使人体感觉到运动平台的角速度，所以倾斜协调通道中的角速度限幅将会严重削弱模拟持续加速度的特性[10]，导致飞行模拟器的动感逼真度进一步下降。王辉等将倾斜协调输入的加速度进行分段比例设计[11]，虽然可以解决信号丢失问题，但是模拟器运动空间限制其进行大加速的模拟；由于采用了多个滤波器，所以滤波器参数调节具有主观性，导致飞行模拟器教练员调节模拟器主观因素增加，难度增大[12]。

本文通过分析和研究飞行模拟器和经典洗出算法的运动特性[13-15]，对经典洗出算法的控制策略进行重新设计，提出一种改进的算法，解决倾斜协调通道低通滤波器信号丢失造成的动感逼真度下降和滤波器参数调节的问题，并通过Matlab/siumlink仿真实验证明该算法的可靠性和有效性。

1 经典洗出算法

经典洗出算法(如图1)由三部分组成：高通加速度通道、倾斜协调通道、旋转角速度通道。高通加速度通道是模拟飞机(滚转、俯仰、偏航三个方向)的瞬间加速度，然后经过洗出后得到所需位移量；倾斜协调通道运用倾斜协调的原理模拟飞机(滚转、俯仰、偏航三个方向)的持续加速度，经过洗出后得到六自由度运动平台角位移的一部分；旋转角速度通道模拟飞机在三个方向的角速度，经过洗出后得到运动平台的角位移的一部分。

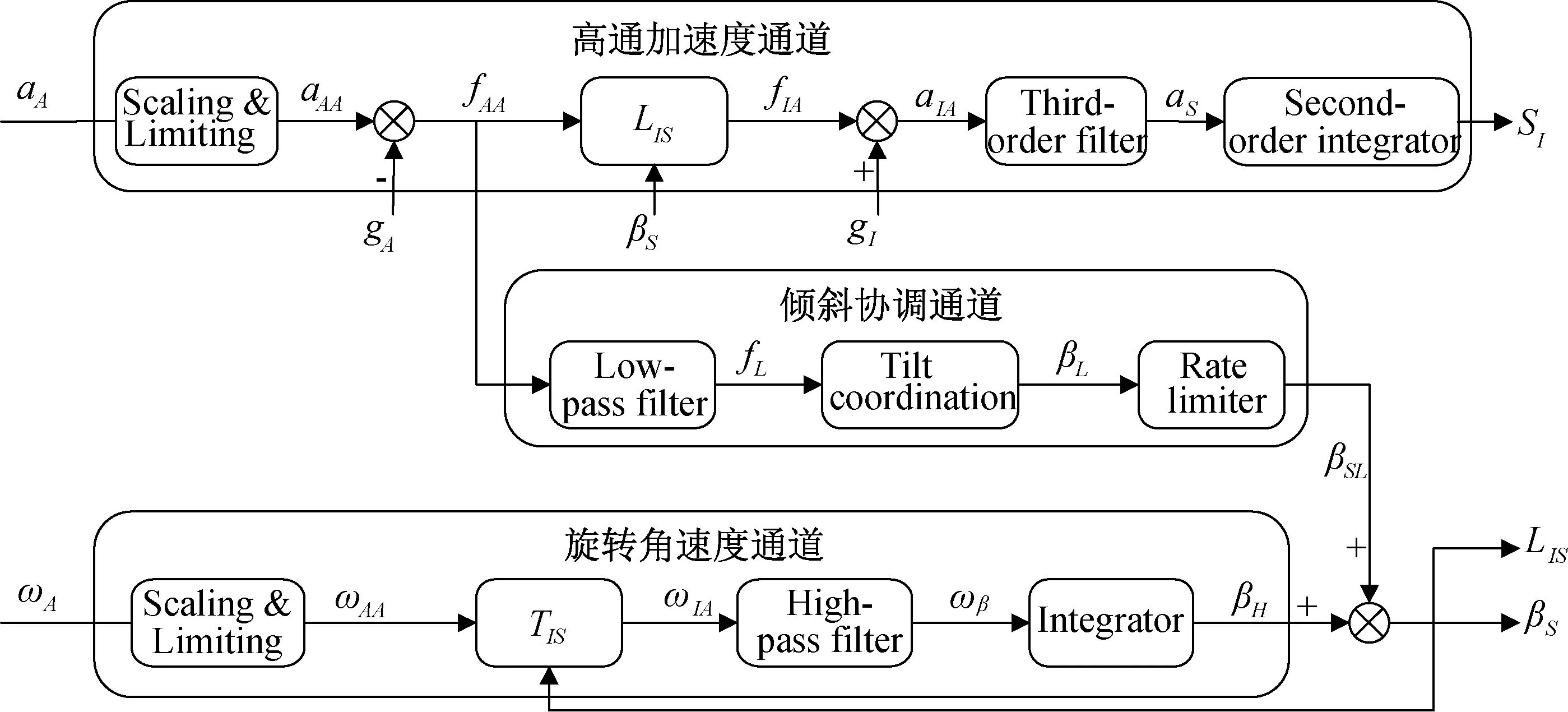
图1 经典洗出算法

高通加速度通道滤波器的传递函数如下：

(1)

低通加速度通道滤波器的传递函数如下：

(2)

高通角速度通道滤波器的传递函数如下：

(3)

式中:ωah、ωm、ωωh、ωal为自然截止频率，ξah、ξal、ξωh为阻尼比。

经典洗出算法的坐标变换，实现飞行模拟器的动坐标系转换为参考坐标系，由式(4)确定：

(4)

其中，c为cos，s为sin，t为tan，φ、θ、φ为运动平台的三个姿态欧拉角，LIS和TIS分别为平移、旋转变换矩阵。

在经典洗出算法中，gI=[0,0,g]为地面参考坐标系的重力加速度，运动平台下重力加速度gA由式(5)确定：

(5)

经典洗出算法姿态角βS的计算如下：

(6)

βS=βSL+βH

(7)

2 人体前庭系统

通过对人体感觉系统的研究和分析，发现人体前庭感官系统的耳石和半规管是接收外界运动信号的主要器官。其中耳石是接受外界线加速度的主要器官，半规管是接受角速度的主要器官。

2.1 耳石模型

耳石是前庭系统中感觉线加速度的主要器官，可感知的比力是相对加速度，即平移加速度减去重力加速度:

fAA=a-g

(8)

(9)

由式(9)可知，人体感觉的比力是由平移加速度和重力加速度共同作用，即人体感觉到的加速度是不能区分由运动还是重力引起——倾斜协调原理。由于人体感官系统是非线性的，Young和Oman用弹簧、质量、阻尼模型近似模拟人体感觉系统，使感觉系统线性化[16]，其传递函数如下：

(10)

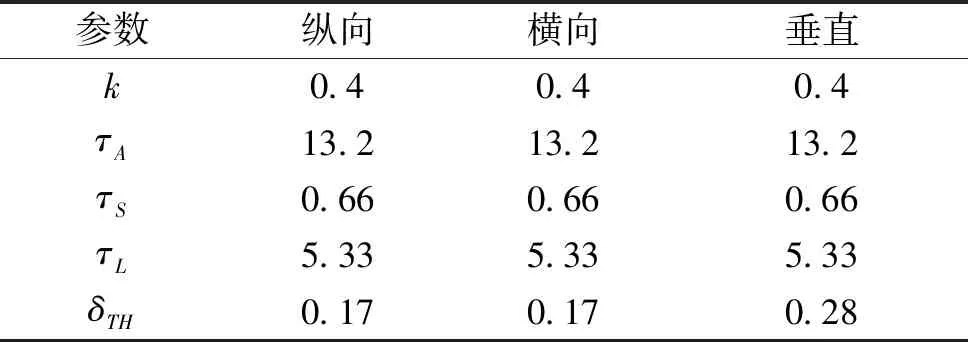
表1 人体耳石模型参数

2.2 半规管模型

半规管是前庭系统中感觉角速度的主要器官，可以感知滚转、俯仰、偏航三个方向的角速度，其传递函数如下：

(11)

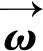
表2 人体半规管模型参数

3 改进洗出算法

倾斜协调通道低通滤波器是为了模拟飞机的持续加速度，其低通加速度来源对飞行模拟器模拟飞机运动状态至关重要。经典洗出算法忽视平移通道与倾斜协调通道的相互耦合现象，直接采用限幅后的比力加速度作为倾斜协调通道低通滤波器加速度的来源，导致最终洗出结果出现相位延迟，且平移通道高通滤波器和倾斜协调低通滤波器的参数对运动洗出效果影响比较大[17]，需要根据不同情况调整滤波器参数，这也是导致经典洗出算法主观因素产生的原因。此外，倾斜协调通道使用重力加速度分量模拟持续加速度同样是被约束在一定角度内，否则会出现驾驶员感觉到运动平台出现倾斜；还需要进一步考虑旋转过程中角速度不能超过半规管阈值，否则驾驶员同样会感觉旋转运动的发生。

针对经典洗出算法的缺陷，本文采用如下方法解决其问题(如图2所示)：考虑到洗出过程中高通平移通道和倾斜协调通道解耦困难，因此，直接使用闭环控制方法来解决其相互耦合的问题。先把平移高通滤波器过滤后的高通加速度转换为运动平台上平台的相对加速度fH，然后通过公式(12)即可获得倾斜协调通道加速度来源；低通加速度fL可以直接经过倾斜协调作用得到倾斜角βL，由于有角速度限幅器的限制，限幅后必然会减小通过的倾斜角，此时需要把未模拟持续加速度的那一部分倾斜角转移到平移通道，其转换结构如式(13)所示。

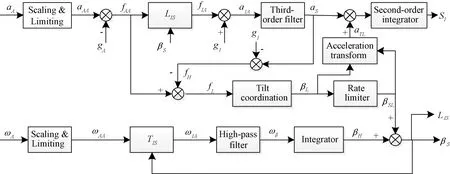
图2 改进洗出算法

fL=fAA-fH

(12)

aTL=(βL-βSL)·g+gI

(13)

4 仿真实例分析

飞行模拟器模拟飞行状态时通常需要完成不同的加速度动作，而飞行模拟器通过组合四种运动方式(纵向/俯仰、横向/滚转、偏航、升沉)可以实现绝大部分的飞行状态。通过图2在Matlab/Simulink中建立改进洗出算法的仿真模型，为不影响输入加速度的效果，限幅环节的参数为1，滤波器参数选择可根据杨宇等[18]研究选择，本文高通滤波器参数如下表3所示，以飞行模拟器的纵向/俯仰运动姿态为例，同时避免角速度的影响，输入的俯仰角速度为零，其纵向加速度为2 m/s2的阶跃加速度(如图3所示)。

表3 高通滤波器参数

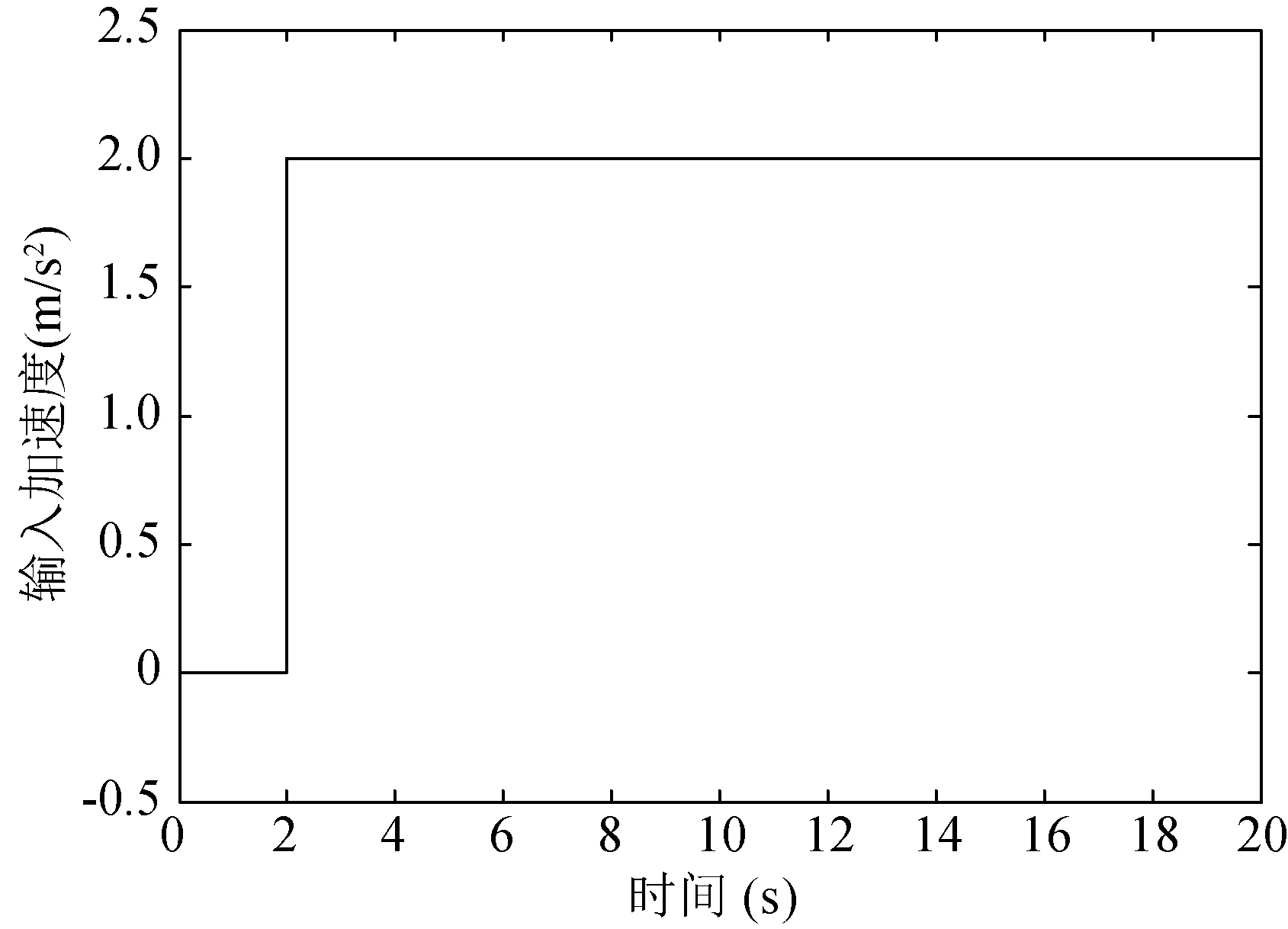
图3 加速度

图4为经典洗出算法和改进洗出算法两种洗出算法的洗出位移对比。从图中可以看出，虽然两种洗出算法洗出位移量基本相同，且在8 s时都到达零位置，说明飞行模拟器的运动平台经过两种洗出算法的控制策略最终恢复到中立位置，可以为下次运动做好准备。但是经典洗出算法在3～7 s时间内位移量为负，说明运动平台向反方向有运动状态，很容易造成驾驶员感知这种虚假暗示，影响飞行模拟器的动感逼真度。通过改进洗出算法的位移曲线可知，其运动平台的纵向位移始终为正，不存在洗出过程的虚假暗示现象，且平台的位移量保持在0.35 m以内，但是洗出位移要高于经典洗出算法，因此，改进洗出算法能够克服经典洗出算法的空间利用过于保守的问题，且不存在负向位移，飞行模拟器的动感逼真度能够保证。

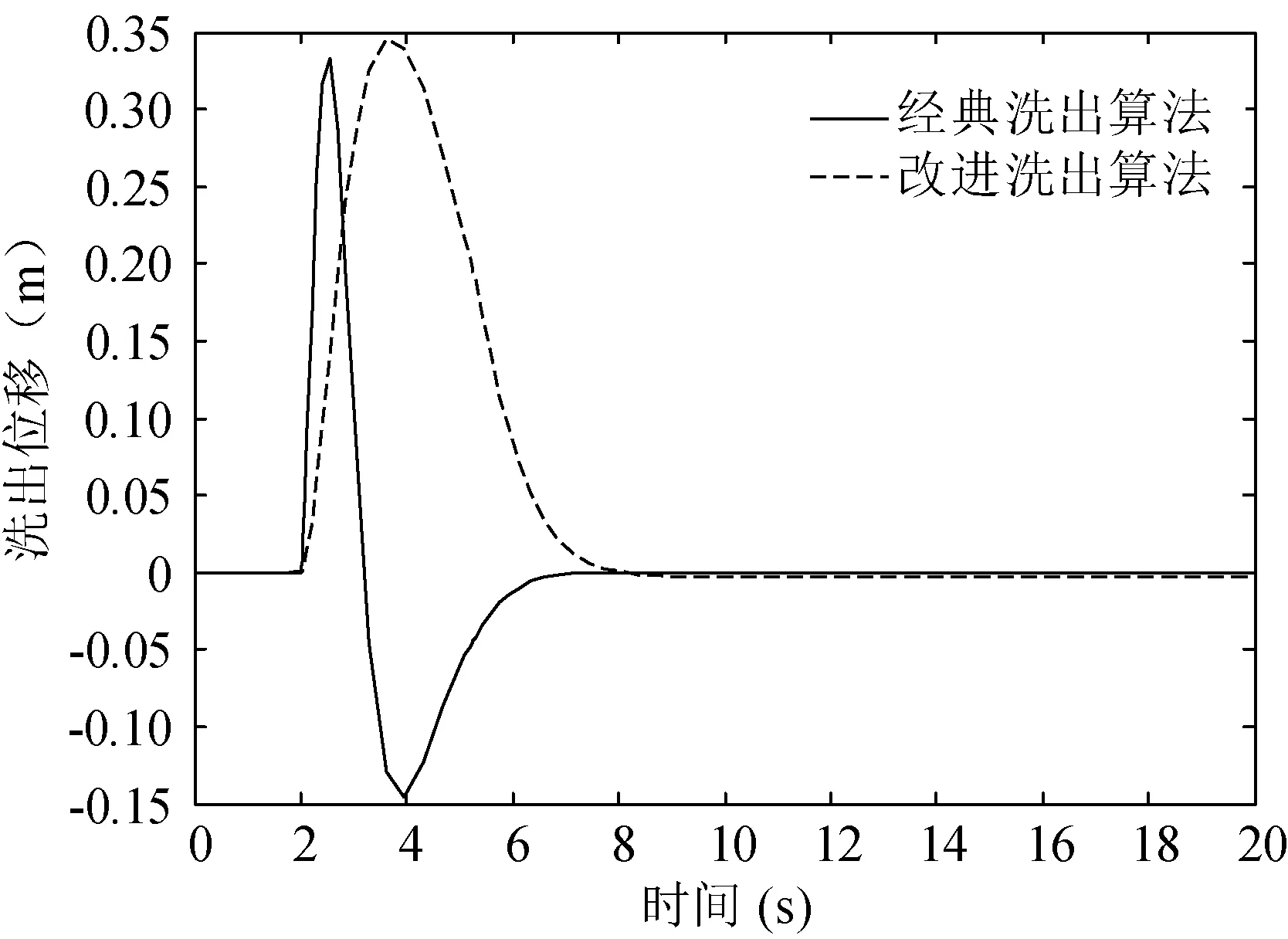
图4 洗出位移

根据半规管模型可知，人的角速度俯仰感知阈值为3.6(°)/s，超过该阈值必然会使人体感觉到倾斜协调的运动，从而导致洗出过程中出现有俯仰方向的感觉角速度。从图5可知，改进洗出算法不影响运动平台洗出的角速度，基本和经典洗出算法相同，洗出的感觉角速度都在感觉阈值内，因此能够保持改进算法的可靠性。图6为运动平台加速度经过低通滤波器和角速度限幅器后洗出的角位移，由于改进洗出算法没有使用低通滤波器来处理倾斜协调的低通加速度，因此不存在倾斜协调信号丢失的问题，能够最大可能保证模拟持续加速的完整性，两种洗出俯仰角位移量最大值为0.2 rad(约为11.46°)，远小于人体可感知角25°。由于改进洗出算法没有使用倾斜协调滤波器，因此减少了飞行训练过程中滤波器参数调节的难度。

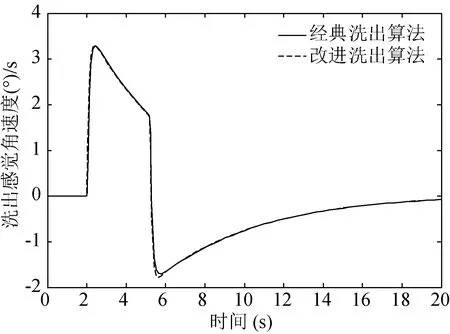
图5 洗出感觉角速度

图6 洗出角位移

人体可感知的洗出加速度是由平移运动通道的平移加速度和倾斜协调的持续加速度组成。由图7可知，其中参考曲线表示未经过洗出算法洗出的感觉加速度，即人感觉到的真实加速度，洗出算法好坏的评价标准就是看洗出感觉运动曲线和参考曲线的接近程度，越接近参考曲线，说明该算法在整体上更符合飞行模拟器的控制要求。从图7中可知改进洗出算法洗出的感觉加速度峰值为1.6 m/s2，和参考曲线基本相同且峰值点相位差仅存在1 s延迟，6 s后参考曲线和改进算法曲线基本重合，说明改进洗出算法对飞行模拟器的控制效果更好，满足人体感知需求。而经典洗出算法与参考曲线峰值点存在3 s的相位延迟，并且在2～6 s时间内洗出感觉加速度与参考曲线同样相差过大，此会造成人坐在驾驶舱中感觉到运动和驾驶的不协调。图8为洗出感觉加速度误差，经典洗出算法由于相位延迟的原因导致误差过大，达到了1 m/s2，已经远远超出人体耳石器官能够区分加速度的阈值，因此在飞行训练过程中极易被感知到，而改进洗出算法则保持误差不超过0.2 m/s2，十分接近耳石器官的阈值，不太容易感觉出飞行模拟器运动过程中的虚假暗示。

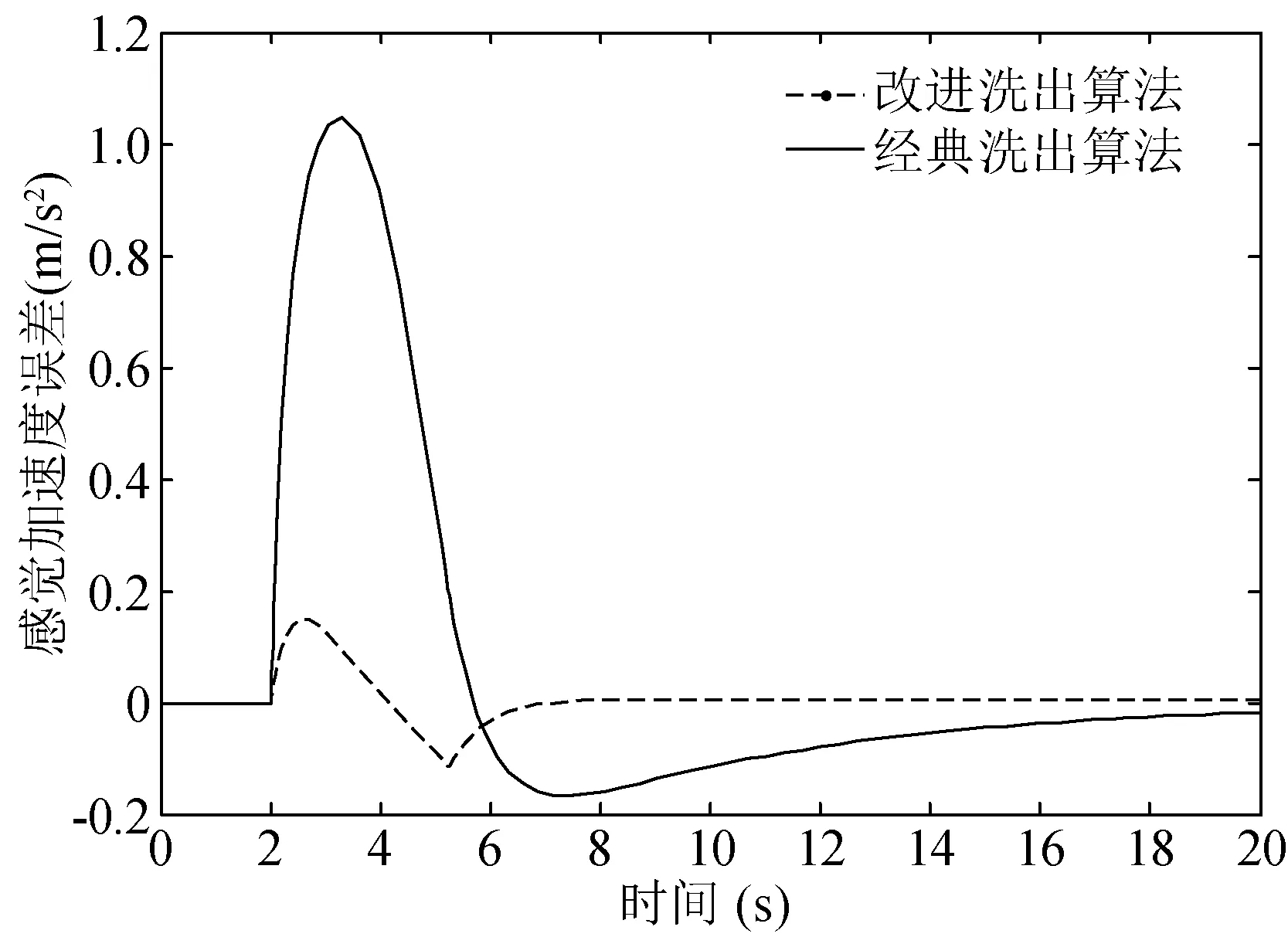
图8 感觉加速度误差

5 结论

对经典洗出算法和飞行模拟器的运动特点进行了分析，重新设计洗出算法的结构，解决经典洗出算法平移通道和倾斜协调通道相互耦合以及角速度限幅导致的模拟持续加速不够完整造成虚假暗示的问题。通过仿真结果分析可知，改进后的洗出算法能够减小洗出过程中的相位延迟，克服平移和旋转方向的虚假暗示现象，对飞行模拟器的洗出效果和动感逼真度有显著提升。对洗出算法结构的设计减少了洗出算法滤波器的数量，在一定程度上可以降低算法参数调节的难度。因此，该改进算法对我国飞行模拟器运动控制系统的理论研究具有借鉴意义。