中厚壁钢管混凝土轴压承载力的计算研究

罗露露 董延龙

(1.武汉交通职业学院，湖北 武汉 430065；2.中南勘察设计院集团有限公司，湖北 武汉 430061)

1 引言

钢管混凝土是在钢管中填充混凝土，混凝土与钢管共同承担外界荷载的结构。两种不同材料之间的相互作用，使钢管混凝土具有承载力高、塑性和韧性好、防火性能好、施工方便以及经济性好等一系列优点，到目前为止已被广泛应用于国内外的工业厂房、多层和高层建筑以及桥梁等结构中。

学者对不同截面形式[1-2]、不同材料性能[3-5]钢管混凝土力学性能影响的研究越来越多，其研究成果亦较为丰富。文献[6]通过试验对自密实自应力的高强钢管混凝土短柱进行了研究，提出了自密实自应力高强钢管混凝土短柱轴压承载力的计算公式。文献[7]基于试验数据，提出了带约束拉杆方形、矩形钢管混凝土短柱轴压承载力计算方法。文献[8]在试验基础之上，研究了不同计算方法在计算矩形钢管混凝土短柱上的差异性，并提出矩形钢管混凝土短柱轴压承载力建议公式。文献[9]分析了圆钢管混凝土柱轴压承载力计算方法的合理性，并修正了长细比在4.0～38.5的钢管混凝土柱轴压承载力的计算公式。关于钢管混凝土轴压承载力的计算研究颇多，但适用于中厚壁及中厚壁带肋钢管混凝土轴压承载力的理论计算公式却并未明确提出。

我国现行规范GB 50936—2014《钢管混凝土结构技术规范》中也给出了圆形、多边形及椭圆形钢管混土承载力的计算方法，但公式是否适用于中厚壁及中厚壁带肋钢管混凝土承载力的计算并未说明。因此，本文拟采用GB 50936—2014《钢管混凝土结构技术规范》中的计算模型，结合作者之前发表的论文中的试验数据，对中厚壁及带肋的中厚壁矩形钢管混凝土轴压承载力进行计算，探讨规范中的计算模型在中厚壁及带肋钢管混凝土结构中的适用性，为中厚壁及带肋的中厚壁钢管混凝土研究的完善和进一步发展提供一定的参考，使中厚壁及带肋的钢管混凝土柱在高层、超高层建筑结构或桥梁结构中的应用，具有更为重大的理论和现实意义。

2 轴压承载力理论计算公式

GB 50936—2014《钢管混凝土结构技术规范》给出了两种适用于圆形、多边形及椭圆形的钢管混凝土轴压承载力的计算方法。

方法一是基于统一理论的计算方法，其核心思想是把钢管和混凝土两种材料看成一种组合材料，组合材料在工作时是统一、连续及相关的，故其轴向承载力计算公式为

N0=Ascfsc

fsc=(1.212+Bθ+Cθ2)fc

其中：N0——钢管混凝土短柱轴压承载力；

As，Ac，Asc——钢管、混凝土截面面积及钢管混凝土全截面面积；

fs，fc，fsc——分别为钢材、混凝土抗压强度设计值及钢管混凝土组合抗压强度值。其中fsc按规范附表B进行取值；

θ——套箍系数；

B，C——截面形状对套箍系数的影响系数,按表1进行计算。对于矩形截面应换算成等效正方形截面进行计算，等效正方形的边长为矩形截面的长短边边长的乘积的平方根。

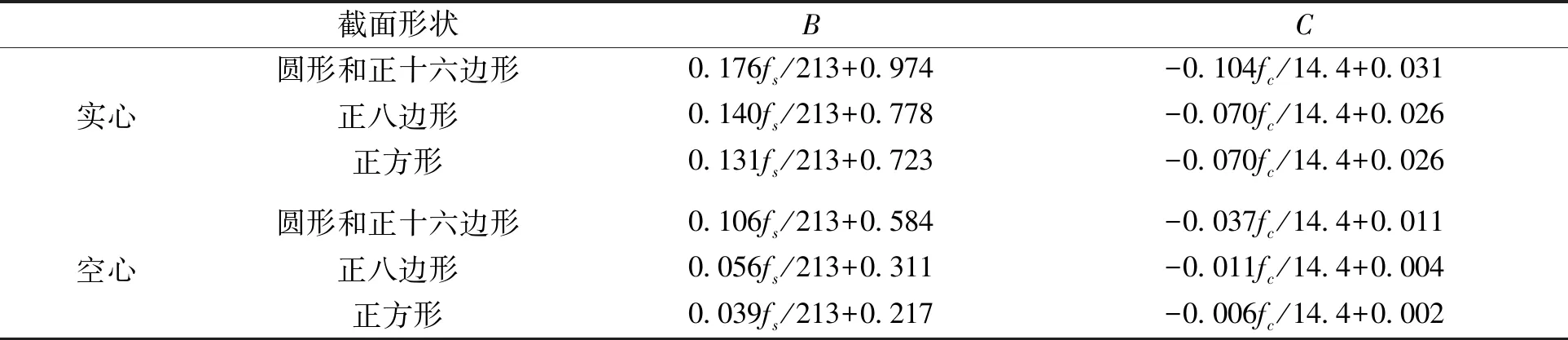
表1 截面形状对套箍系数影响系数B、C取值

方法二是极限平衡理论计算，该方法是在不用确定钢管及混凝土本构关系的基础之上，直接观察试验建立钢管混凝土承载力计算公式，具体计算公式如下所示：

N0=0.9Acfc(1+αθ)

式中：α——与混凝土强度等级有关的系数，当混凝土强度≤C50时，α=2.0；C50～C80之间时，α=1.8。

3 轴压承载力试验值

文献[10]中采用试验研究和理论研究相结合的方式，对中厚壁钢管混凝土短柱及中厚壁带肋的钢管混凝土短柱进行了轴压承载力试验研究。混凝土材料采用加减水剂和6%水泥膨胀剂的C30自密实混凝土，钢材分别采用6 mm壁厚的Q345钢及10 mm厚的Q235钢，制作了5种截面形式，共10个试件。试件截面形式如下图1所示。其中a、b、c、d、e截面分别为无加劲肋截面、单向单排肋宽40 mm截面、双向单排肋宽40 mm截面、双向单排肋宽60 mm截面以及双向双排肋宽40 mm截面。

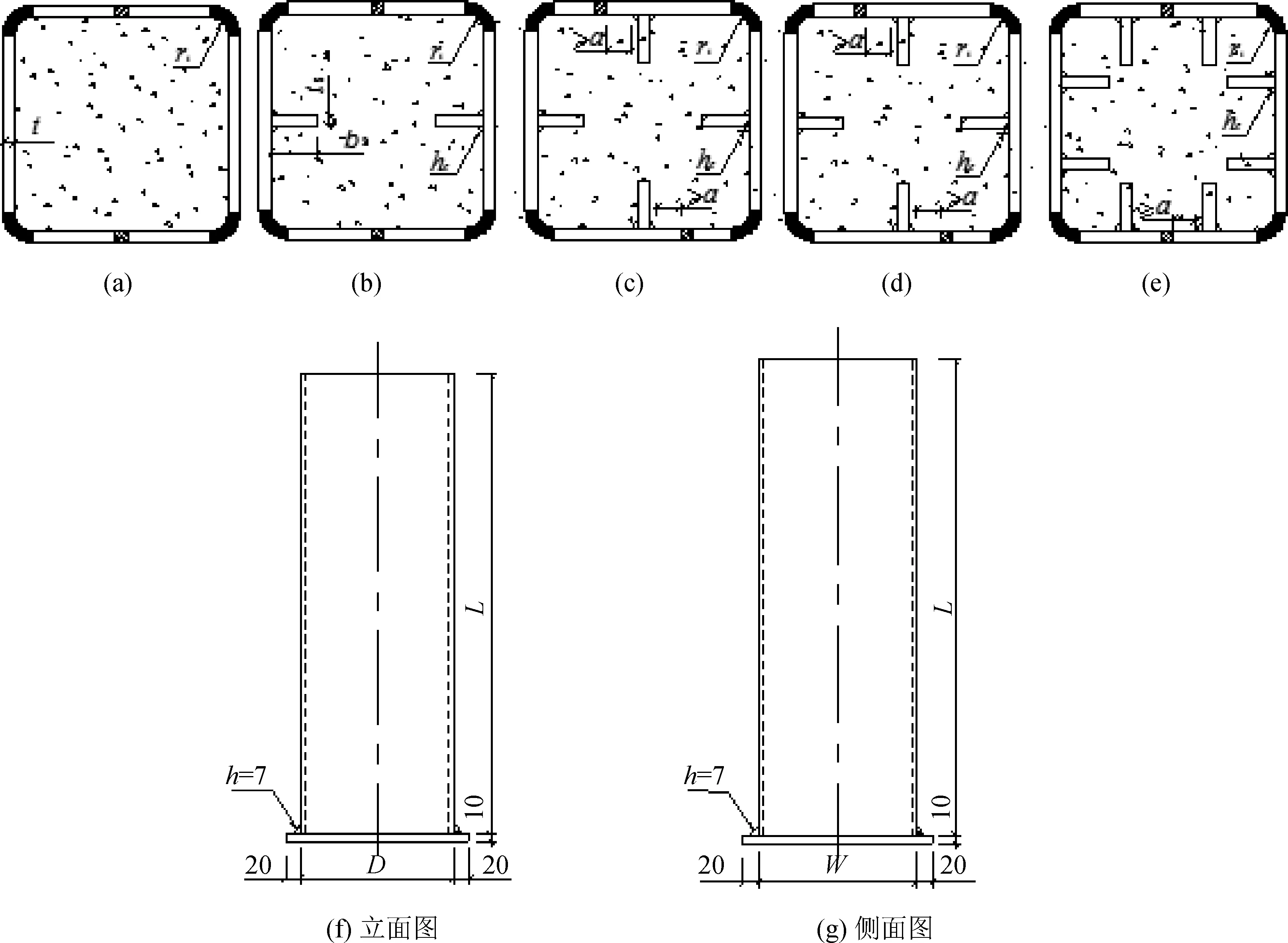
图1 试件截面

通过试验研究得到各试件的轴向极限荷载，并用ANSYS建模软件进行建模分析，最终ANSYS分析结果与试验值较吻合，验证了试验数据的可靠性。试验结果如表2所示。表中编号第一个字母代表截面形式，第二个数字代表钢管壁厚。如c-6表示6 mm双向单排肋宽40 mm截面形式。Nu为钢管混凝土截面的试验值。

表2 文献[10]中试验值(单位：kN)

4 轴压承载力计算值与试验值对比结果分析

将文献[10]中试件的相关参数代入GB 50936—2014《钢管混凝土结构技术规范》所示轴压承载力公式中进行计算，其计算结果如表3所示。其中NuG1代表采用GB 50936—2014方法一基于统一理论的计算方法计算出的极限值，NuG2代表采用GB 50936—2014方法二极限平衡理论计算出的极限值。

表3 轴压承载力计算值(单位：kN)

将规范计算值与作者论文中的试验值进行对比分析，其分析结果如表4及图2所示。

表4 规范计算值与试验值对比分析结果

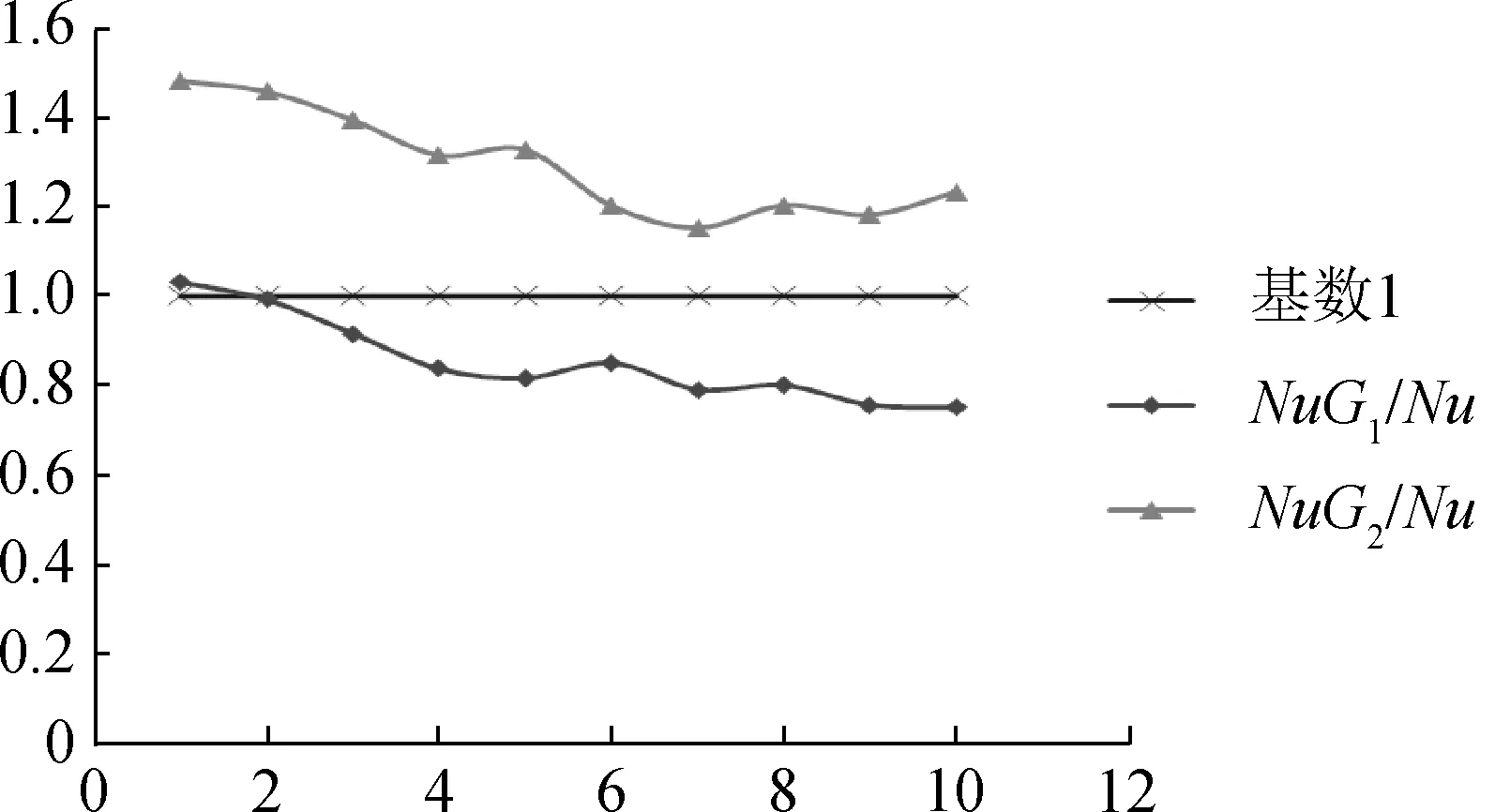
图2 规范计算值与试验值对比分析图

对表4和图2进行分析，结果如下：

1)规范中方法一计算模型的计算值与试验值对比误差值在-0.25～+0.03之间，除了a-6试件，其他试件计算结果均小于试验值。

2)规范中方法二计算模型的计算值与试验值对比误差值在0.23～0.48之间，其计算结果均大于试验值。

3)方法一用于计算6 mm壁厚试件的计算结果与试验值更为接近。6 mm壁厚a、b、c、d、e试件计算值与试验值的误差分别为+3%、-1%、-8%、-16%、-18%，其误差平均值为-8%；10 mm壁厚a、b、c、d、e试件计算值与试验值的误差分别为-15%、-21%、-20%、-24%、-25%，其误差平均值为-21%。

4)方法二用于计算10 mm壁厚的截面计算结果与试验值更为接近。6 mm壁厚a、b、c、d、e试件计算值与试验值的误差分别为48%、46%、39%、32%、33%，其误差平均值为39.6%；10 mm壁厚a、b、c、d、e试件计算值与试验值的误差分别为20%、15%、20%、18%、23%，其误差平均值为19.2%。

5 结论

1)GB 50936—2014《钢管混凝土结构技术规范》中轴压承载力的两种计算模型均可为中厚壁钢管混凝土及中厚壁带肋钢管混凝土轴压承载力的计算提供一定的参考。

2)GB 50936—2014《钢管混凝土结构技术规范》中基于统一理论计算模型的计算结果更为准确，极限平衡理论计算结果均高于试验值。方法一、方法二计算模型的计算值与试验值误差平均值分别为-14.59%、29.47%。

综上所述，现行规范GB 50936—2014《钢管混凝土结构技术规范》的计算公式能够为中厚壁及中厚壁带肋钢管混凝土轴压承载力的计算提供一定的参考，但其计算结果存在一定的误差，后续可以以规范中的计算公式为基础，对其进行修正，使其对该种形式的钢管混凝土结构的计算结果更为精确，让中厚壁及带肋的中厚壁钢管混凝土柱在高层、超高层建筑结构或桥梁结构中的应用，具有更为重大的理论和现实意义。